粉质黏土强度特性应变速率效应的试验研究

胡田飞，刘建坤，刘振亚，刘 昕，3

(1.北京交通大学 土木建筑工程学院，北京 100044；2.石家庄铁道大学 土木工程学院，河北 石家庄 050043；3.青海大学 地质工程系，青海 西宁 810016)

由于土的碎散性、不均匀性及具有三相体特征，其工程性质除受控于自身颗粒级配、矿物成分及结构等因素外，还受到应力历史、环境温度、地下水、时间及荷载等因素的影响[1-3]。其中，应变速率也是影响土体变形特征和力学性质的重要因素，应变速率效应是土体流变性的主要特征之一[4]。

关于黏性土变形和强度特性的应变速率效应，目前已有大量的研究。文献[5-6]发现黏性土的不排水抗剪强度和弹性模量会随应变速率的增加而增大。文献[7]发现黏性土极限强度与应变速率的正相关现象，并认为该现象是由剪切产生的孔隙水压力和土骨架本身的黏滞性单独或共同作用引起的。文献[8-9]基于各向异性弹黏塑性本构关系分析应变速率对不排水抗剪强度的影响，计算结果均表明不排水抗剪强度与应变速率成正比，并证明该现象与土体的固结状态和试验类型无关。但是，也有一些研究结果表明土体强度与应变速率并非单调的正相关关系。文献[10]研究发现结构性黏土存在应变速率软化现象，同时存在一个临界应变速率，小于临界值时强度峰值为应变速率的增函数，大于临界值时则为减函数，且高围压下应变速率的影响小于低围压条件。文献[11-12]研究发现黄土不排水抗剪强度和黏聚力随应变速率的增加先增大、后减小，而内摩擦角则基本随应变速率的增加线性减小。文献[13]研究发现强结构性黏土的抗剪强度随应变速率的增加呈先减小、后增大的规律，黏聚力与内摩擦角则分别减小和增大。文献[14]认为当应变速率较小时，随着固结比的增加，黏土不排水抗剪强度的应变速率敏感度不断降低。文献[15]进一步指出强度的应变速率效应仅取决于次固结系数与压缩指数的比值，与固结应力、固结历史和试验类型无关。可以发现，应变速率对抗剪强度的影响规律并无一致结论，出现了单调增大、先增大后减小和先减小后增大等不同趋势，且这一现象的机理尚不明确。

随着高速铁路、高速公路及重载铁路的发展，高填方和行车荷载作用下路基填料的应变速率效应也受到关注。文献[16]通过排水三轴试验发现砂砾料强度随应变速率的增加而减小。文献[17]通过标准砂的直剪试验发现当法向应力较小时，抗剪强度与应变速率基本无关；法向应力较大时，抗剪强度则随应变速率的增加而减小。文献[18]研究发现级配粗粒土的最大偏应力和扩容现象随应变速率的增加而增强，颗粒破碎率相对降低。文献[19]通过三轴试验发现级配碎石的弹性模量、峰值强度及残余强度均随应变速率的增加而增大。上述研究明确了无黏性颗粒土的应变速率效应，并认为其主要由颗粒的重新排列和破碎程度引起。但是，涉及黏性土填料的研究还较少。

目前，路基填土还较多地采用粉质黏土，《土工试验方法标准》[20]建议粉质黏土不固结不排水试验的应变速率取0.5%/min～1.0%/min，固结不排水试验则取0.05%/min～0.1%/min，其与实际工程常见的应变速率范围10-3%/h～10-2%/h有很大差别[21]。一般来说，应变速率小于10-4s-1时为静态试验，10-4～102s-1为准动态试验，后者涉及排水、排气是否及时对强度的影响，因此不能很好地考虑强度的时间效应和应变速率效应。但是，以往的试验多为饱和土的准动态试验，低应变速率下的试验结果相对较少，同时浅层地表土体多处于非饱和状态。因此，研究非饱和粉质黏土在10-7～10-3s-1范围内的应变速率效应具有更完整的工程意义。

针对这一问题，本文以非饱和压实粉质黏土为对象，通过不排水三轴试验测定应变速率为5×10-7～1×10-3s-1和围压为50～400 kPa时的应力-应变曲线，探讨不同围压和应变速率下试样破坏形式、峰值强度、峰值应变、弹性模量、抗剪强度参数的变化规律及内在机理，以期为粉质黏土路基的应变速率效应分析、设计计算和稳定性评价等工作提供参考。

1 试验材料及方案设计

试验用土取自青藏高原，颗粒级配如图1所示，其常用于该地区的道路工程建设。根据文献[20]中土样和试样的制备要求，土料翻晒烘干后过2 mm筛进行试验。土样的最大干密度为1.828 g/cm3，最优含水率为14.8%，相对密度2.64，液限28.0%，塑限17.7%，塑性指数10.3，定名为粉质黏土。采用分层击实法，在最优含水率和压实度95%条件下制取直径39.1 mm、高80 mm的圆柱体试样，饱和度为78.1%。

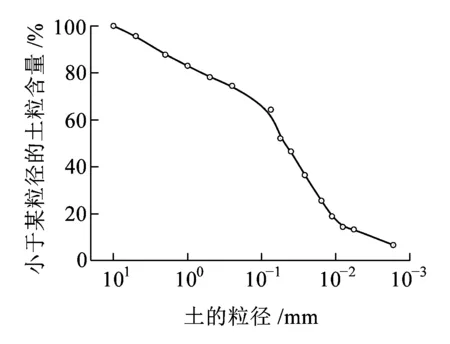
图1 土体颗粒级配曲线

黏性土填方路基沉降主要由孔隙气压缩及排气引起，排水固结变形只占其中小部分。同时，由于低渗透性特征和压实过程的超固结应力历史，以及赋存环境和行车荷载条件，黏性土路基的固结、蠕变过程通常仅在加载瞬间出现增大现象，随后趋于稳定[22]。因此，对于历时较短加载条件下压实黏性土的变形和强度特性，三轴试验应选择为不固结不排水(排气)类型。围压选取低水平(50、100、150 kPa)和高水平(200、300、400 kPa)共计6个级别。轴向应变速率选取5×10-7、1×10-6、2.5×10-6、5×10-6、1×10-5、2.5×10-5、5×10-5、1×10-4、2.5×10-4、5×10-4、1×10-3s-1共计11个级别。试验终止条件为轴向应变达到20%，试验历时2×102～4×105s不等。

考虑到试验工作量，主要选用2台南京土壤仪器厂生产的TSZ-1型三轴仪进行试验，两者标定值一致。同时，为验证试验结果的合理性和内在机理，利用GDS非饱和土三轴仪确定试样在典型试验条件下的体积变化特征。

2 试验结果及分析

2.1 应力-应变关系

图2为试样在不同围压和应变速率下的应力-应变曲线。从图2可以看出，不同围压下，应变速率效应随轴向应变的增加逐渐体现出来，在结构屈服应力附近尤其明显。试样处于低围压时，高应变速率对应的应力-应变曲线为应变软化型。随着应变速率的降低，曲线形式逐渐向应变硬化型过渡，即存在应变速率软化现象。在高围压下，不同应变速率对应的应力-应变曲线均呈应变硬化型。随着围压的增加，应变硬化程度逐渐提高，且不同应变速率对应的应力-应变曲线的差异也逐渐减小。

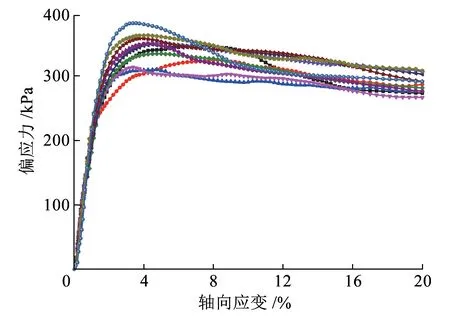
(a)围压50 kPa

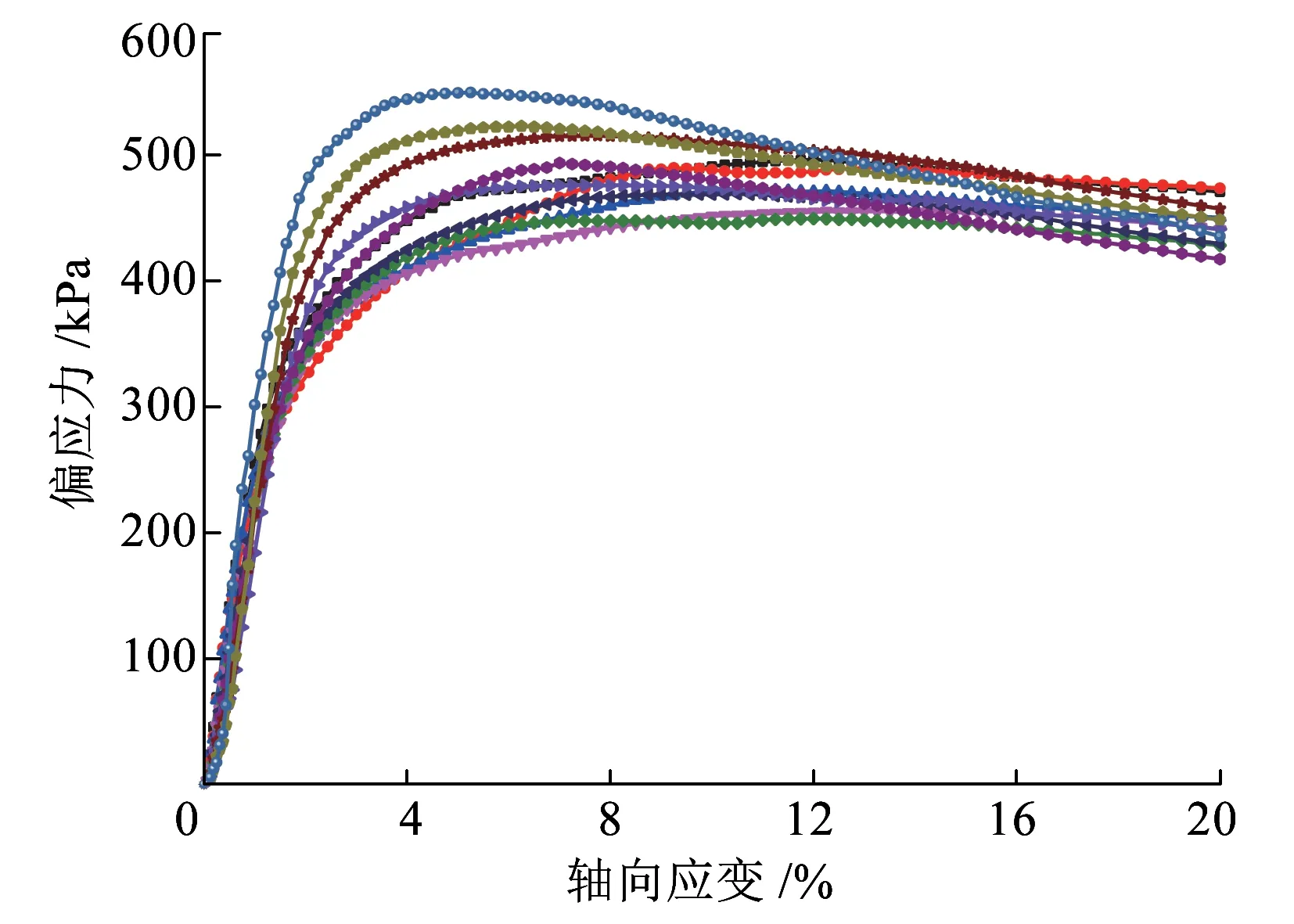
(b)围压100 kPa

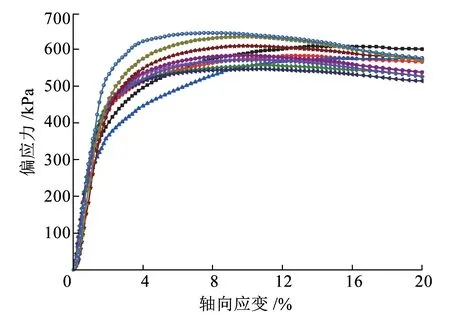
(c)围压150kPa

(d)围压200 kPa

(e)围压300 kPa

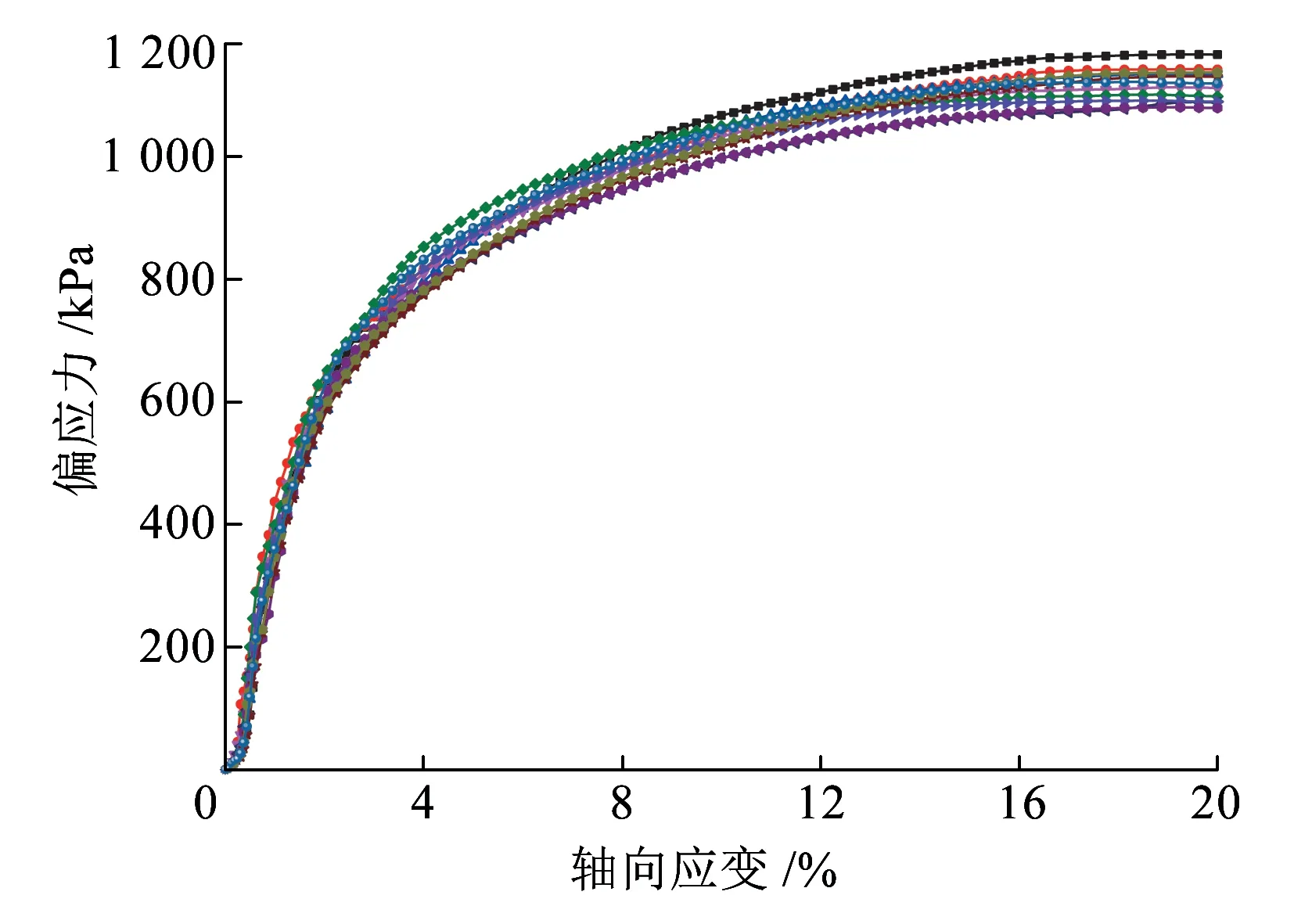
(f)围压400 kPa

图2 不同围压和应变速率下的偏应力-轴向应变关系曲线

2.2 破坏形式

图3为不同围压和应变速率下试样的破坏形态。在低围压下，试样在高应变速率时形成贯通的单向剪裂面，裂纹长度大且外观明显，呈脆性破坏(图3(a))。随着应变速率的减小，剪裂面位置向下移动(图3(b))，并逐渐呈现双向剪切破坏形式，破坏程度相对降低(图3(c))。在高围压下，应变速率较大时试样仅形成不明显的剪切变形带，肉眼可以识别(图3(d))；应变速率较小时，则产生塑性鼓胀破坏，无明显破裂面(图3(e))，与文献[1]的试验结果一致。围压越高，鼓胀程度越低(图3(f))。因此，试样破坏形式与应变速率相关，随着围压的增大和应变速率的减小，土体从局部剪切破坏形式向全面剪胀破坏形式转变。

(a)50 kPa，5×10-4 s-1 (b)50 kPa，1×10-4 s-1

(c)50 kPa，5×10-6 s-1 (d)200 kPa，5×10-4 s-1

(e)200 kPa，5×10-6 s-1 (f)400 kPa，5×10-4 s-1图3 不同围压和应变速率下试样的破坏形态

2.3 峰值强度

不同试验条件下的峰值强度结果见表1。应变速率对不排水抗剪强度的影响程度通过峰值强度变化率来定义

( 1 )

式中：Su为某一应变速率时的峰值强度；Su0为参考应变速率下的峰值强度。文献[20]建议的应变速率范围为0.5%/min～1.0%/min，1×10-4s-1在该范围内，为便于对比，以1×10-4s-1为参考应变速率。

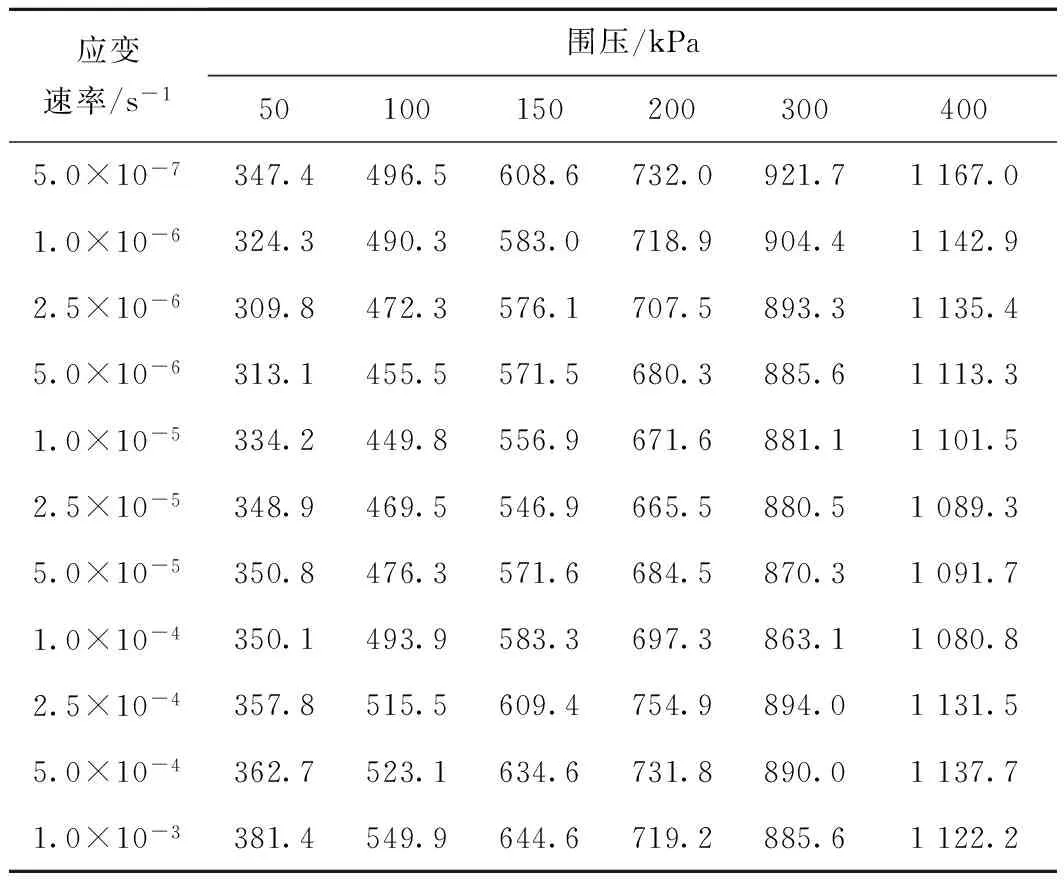
表1 峰值强度统计

图4为不同围压下试样峰值强度变化率与应变速率的关系曲线。从图4可以看出，在不同围压下，低应变速率和高应变速率范围内分别存在一个强度变化率峰值。同时，在低围压下，存在临界应变速率，使得峰值强度变化率随应变速率的增加呈先减小、后增大的规律；而在高围压下，峰值强度变化率随应变速率则呈先减小、后增大、再减小的规律，本文将两个临界点分别称为第一类和第二类临界点。

由此可知，三轴试验得到的粉质黏土不排水抗剪强度与工程实际情况有差异。当实际应变速率高于规范建议值时，峰值强度的试验值在不同围压下均低于实际值；当实际应变速率低于规范建议值时，在低围压下试验值高于实际值，而在高围压下试验值则一般低于实际值。即对于路基填料常见的围压水平和应变速率而言，室内试验结果是普遍偏高的。

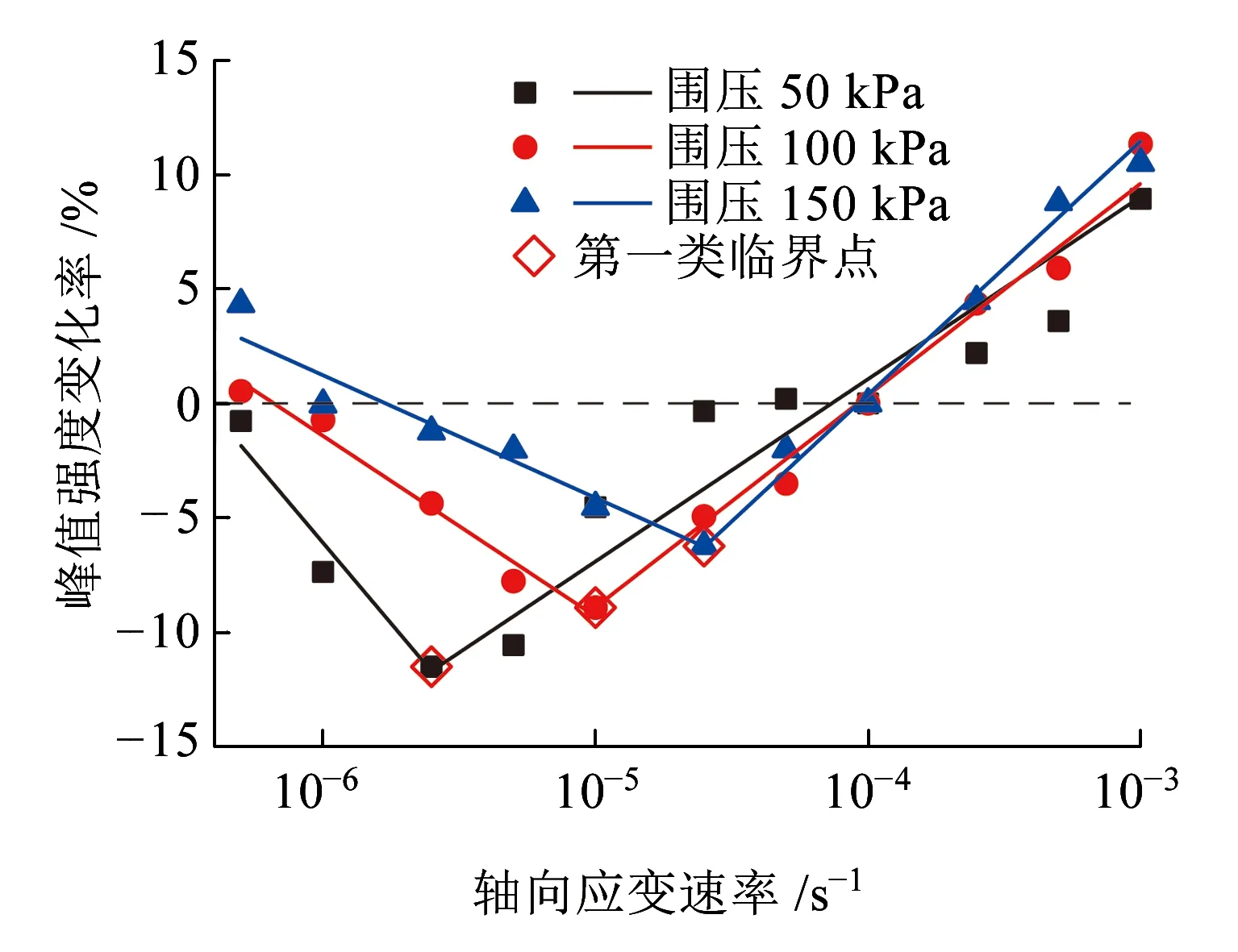
(a)低水平围压

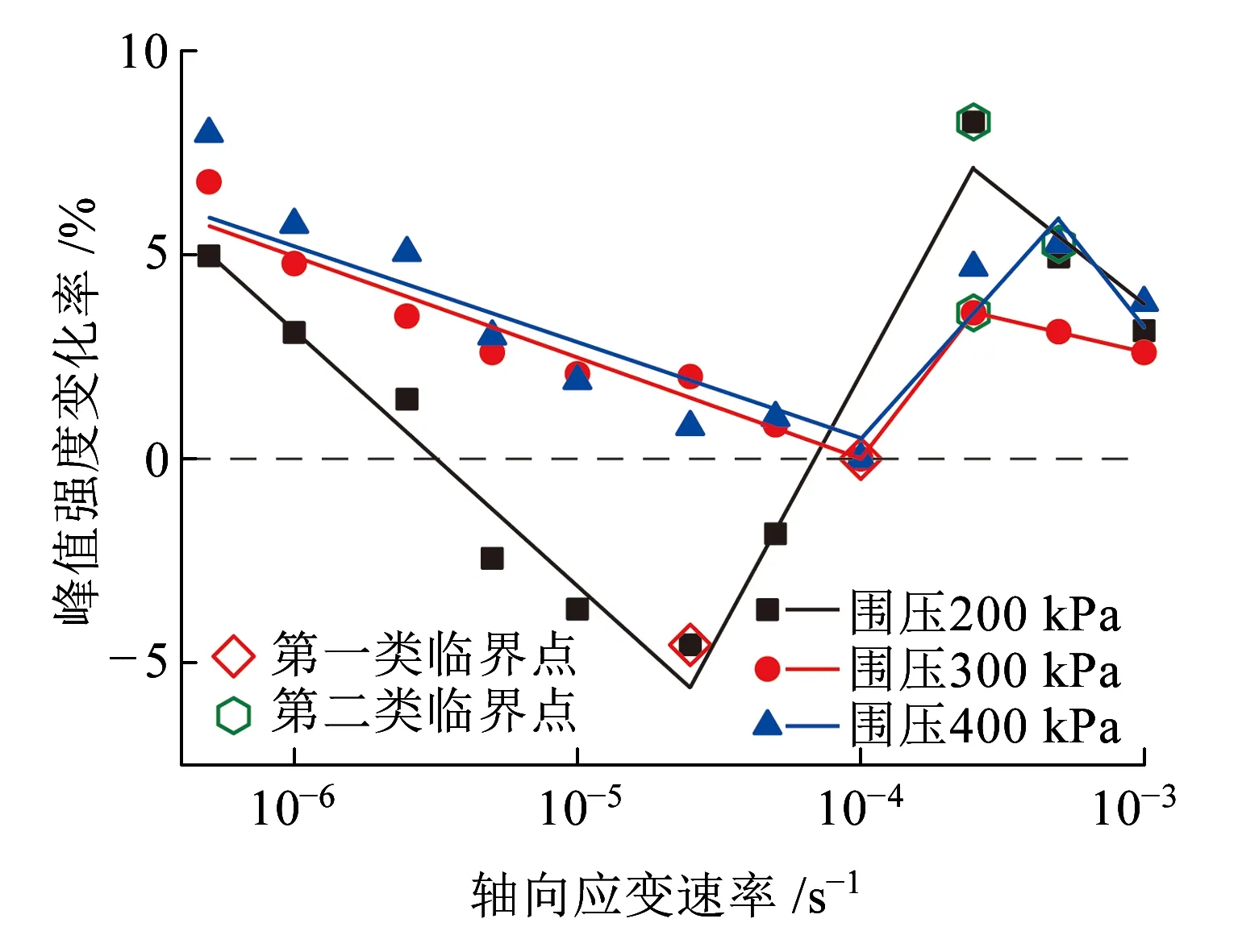
(b)高水平围压图4 峰值强度变化率-应变速率关系曲线

同时，可以采用分段线性函数拟合峰值强度变化率与应变速率的关系，如式( 2 )所示。拟合参数取值见表2。

( 2 )

式中：y为峰值强度变化率，%；x为应变速率,s-1；a1～a3和b1～b3为拟合参数；ε1和ε2分别为第一类和第二类应变速率临界值，s-1。

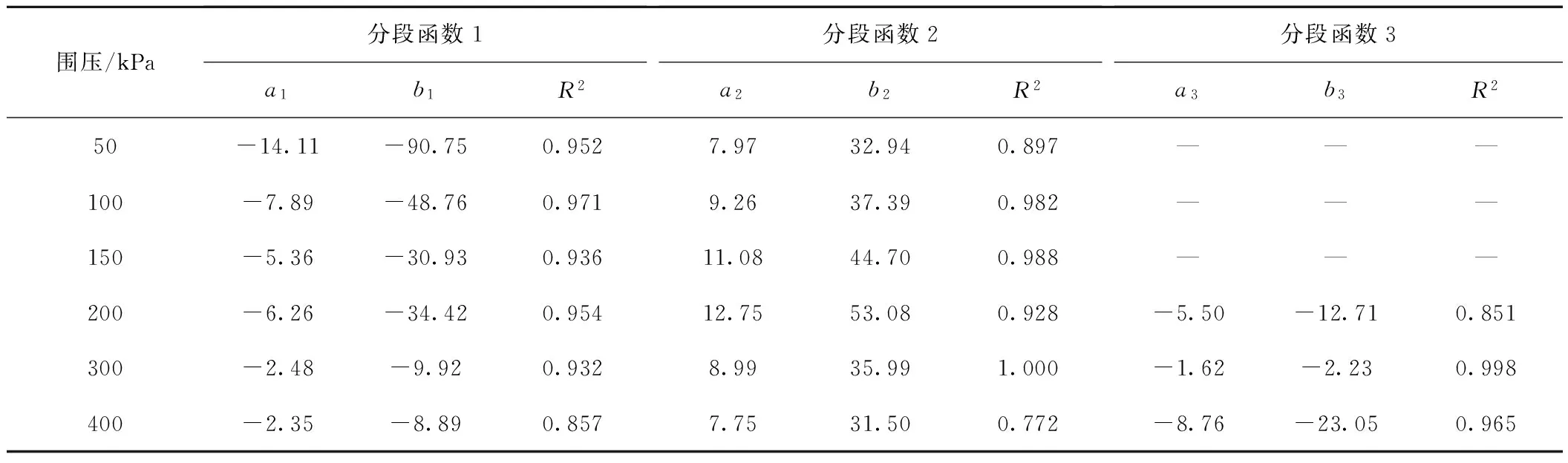
表2 峰值强度拟合参数取值

因此，通过式( 2 )就可以根据某一应变速率下的室内试验结果求解其他应变速率下的不排水抗剪强度，以方便工程应用。此外，在低应变速率时，拟合线斜率绝对值随围压的增加而减小，说明随着围压的增加，应变速率对峰值强度的影响程度逐渐减弱。但是大于第一类临界应变速率之后，围压对应变速率效应的影响则不明显。

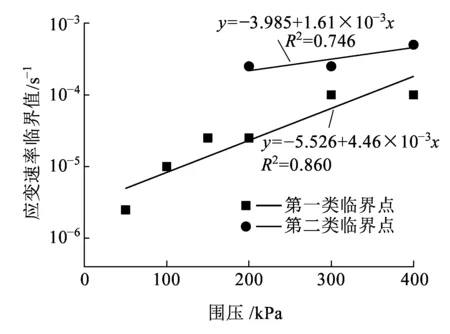
图5 应变速率临界值-围压关系曲线

图5为峰值强度变化率临界点对应的应变速率与围压的关系曲线。从图5可以看出，第一类和第二类应变速率临界值对数均随围压的增加近似线性增大，且第二类临界点只有在高围压下才会出现。本文中，准动态加载范围内(轴向应变速率大于10-4s-1)，峰值强度在低围压下随应变速率逐渐增大，在高围压下先增大、后减小的现象在文献[5-12]中已有体现。但是，在静态加载范围内(轴向应变速率小于10-4s-1)，峰值强度在低围压下先减小、后增大，和在高围压下逐渐减小的试验结果则相对较少。

2.4 峰值应变

峰值应变指峰值强度对应的应变，是工程中直接量测和控制的常用物理量之一。峰值应变越大表明土体的延性越强，反之则脆性越强。图6为不同围压下峰值应变与应变速率的关系曲线。从图6可以看出，峰值应变均随应变速率对数值的增加近似线性减小。同时，拟合直线的斜率基本随围压的增大而减小，即应变速率对峰值应变的影响程度随围压的增大而降低。在围压50 kPa时，由于试样应变软化性较明显，峰值应变集中在5%范围内，故拟合直线斜率绝对值较小；而在围压400 kPa时，峰值应变基本不再受到应变速率影响。这说明，应变速率越大或者围压越低，峰值应变越小，试样脆性越明显，不利于工程稳定性。

2.5 弹性模量

弹性模量是表征土体刚度和变形特性的主要参数。根据图2所示应力-应变关系曲线，选取轴向应变1.5%和0.5%对应的偏应力增量与轴向应变增量的比值作为弹性模量，结果如图7所示。从图7可以看出，弹性模量随围压的增加而增大。在低围压下，弹性模量随应变速率的增加基本呈逐渐增大的趋势；在高围压下，弹性模量随应变速率的增加则呈先减小、后增大的变化规律。弹性模量与应变速率的关系可以采用二次多项式函数y=a(lgx)2+blgx+c进行拟合，拟合参数取值见表3。

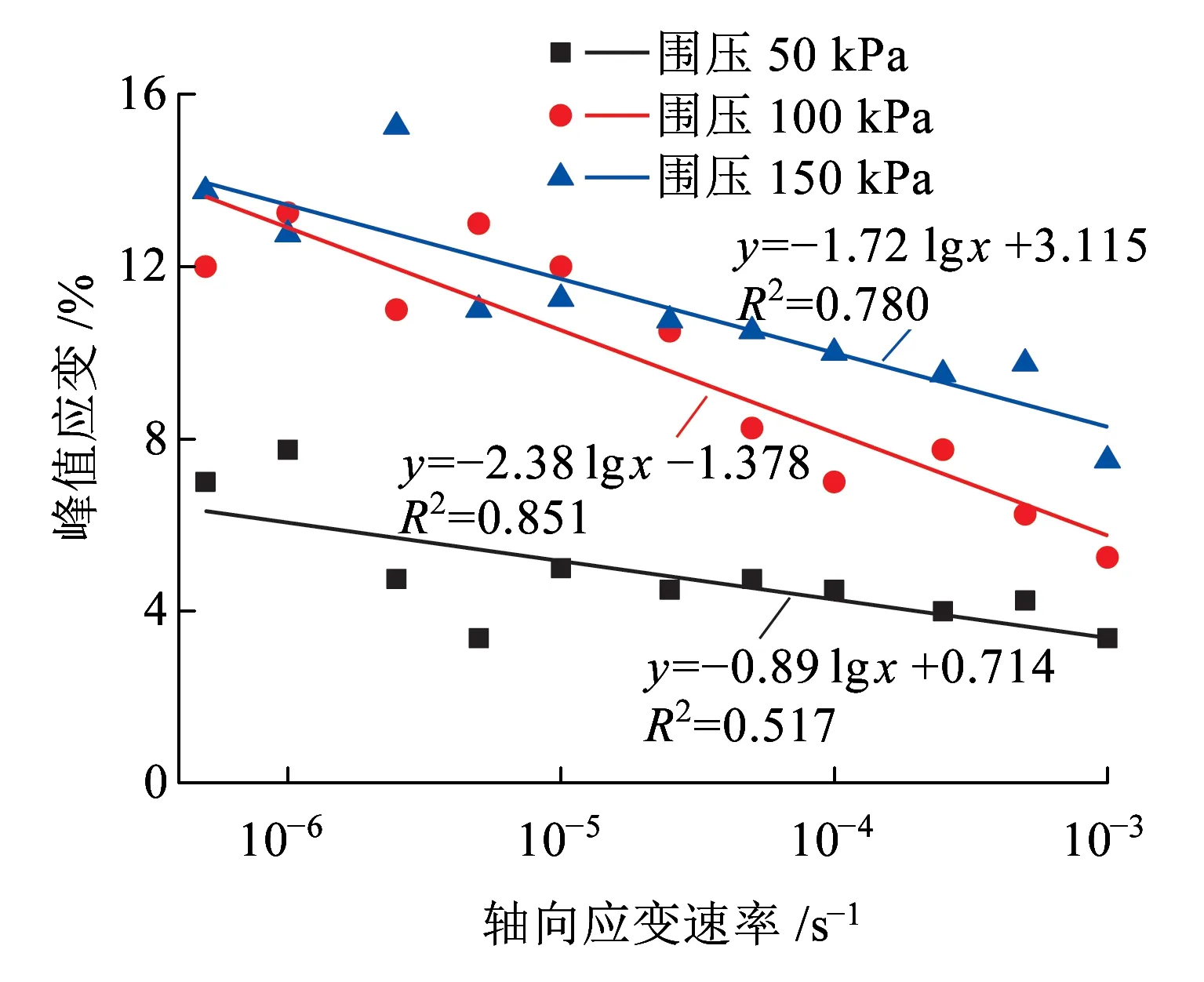
(a)低水平围压

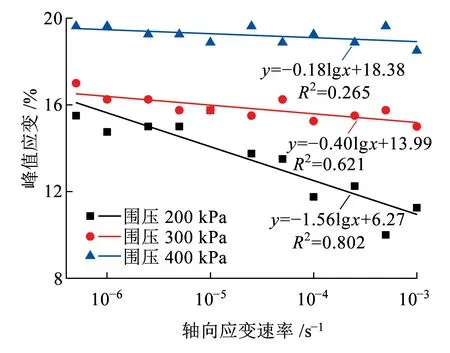
(b)高水平围压图6 峰值应变-应变速率关系曲线

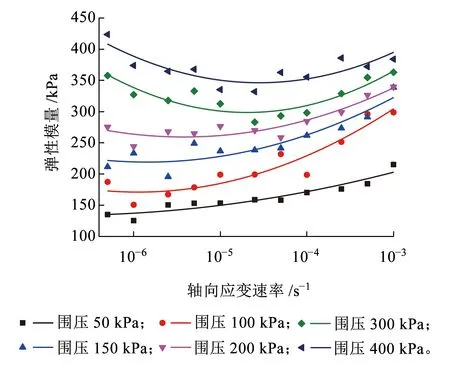
图7 弹性模量-应变速率关系曲线

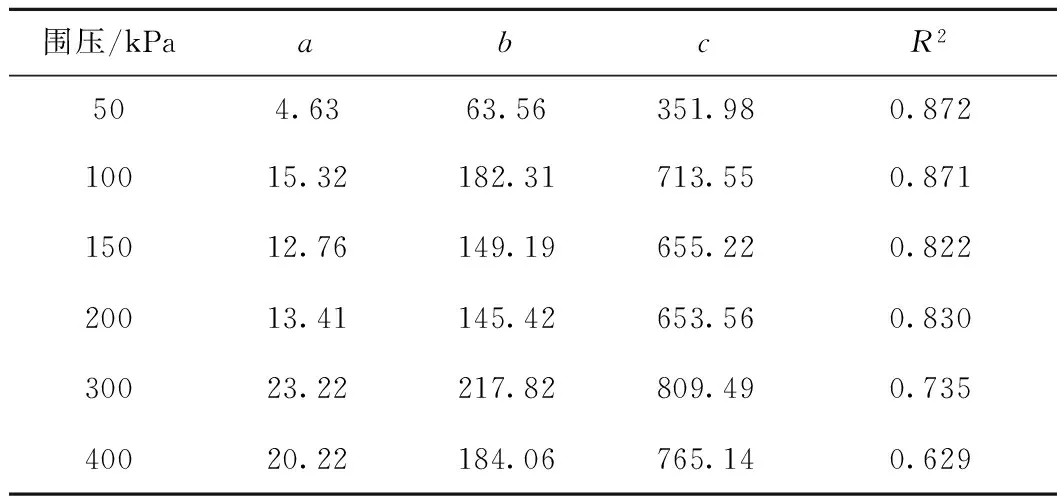
围压/kPaabcR2504.6363.56351.980.87210015.32182.31713.550.87115012.76149.19655.220.82220013.41145.42653.560.83030023.22217.82809.490.73540020.22184.06765.140.629

3 土体的应变速率效应机制

土体的应变速率效应实质上是变形时间效应的一种表现形式。非饱和土的变形是土骨架以及孔隙水、孔隙气综合作用的结果。因此，非饱和土的应变速率效应除受到土骨架黏滞性影响外，还受到孔隙水压力、孔隙气压力和颗粒破碎与接触点受力形式改变等因素的综合影响[23-24]。

3.1 黏滞性的应变速率效应

传统的应变速率效应理论一般认为土的不排水抗剪强度随应变速率对数线性增大，将这一正相关现象的本质归因于土骨架本身的黏滞特性[1]。关于这一因素目前已有定论，一般认为应变速率越大，土骨架黏滞性效应越明显。此外，当土体含水率降低，或在高围压下压缩挤密时，结合水膜变薄，土颗粒约束力增大，黏滞系数升高，蠕变性就不明显。

3.2 固结作用的应变速率效应

非饱和土在荷载作用下同样产生压缩变形和固结，包括孔隙气体、自由水以及结合水转化为自由水的运动和排出[25]。文献[26]认为，即使在不排水条件下，压实土在围压和偏应力的作用下仍然可能产生固结效应。那么，由于土中水和气体运移速度的影响，即使试样达到相同的轴向应变，固结作用也会随加荷时间的不同而有区别。

图8为试样在围压150 kPa和三种不同应变速率下的体积变化量-应变曲线。从图8可以看出，剪切过程中试样体积均呈先减小、后增大的规律。应变速率为1×10-6s-1时，轴向应变11%之前试样持续排气剪缩，孔隙减小，干密度增大，进而引起土体强度增加，即固结效应。随着应变速率的增加，剪缩量峰值及对应的轴向应变逐渐减小，而最终的剪胀量逐渐增大，说明固结效应随应变速率的增大而减弱。原因在于，应变速率较小时，土中孔隙水、气有足够时间排出，试样压密固结；而应变速率较大时，土中水、气来不及运移和排出。当应变速率为1×10-4s-1时，试样基本处于剪胀状态，基本不存在固结作用。

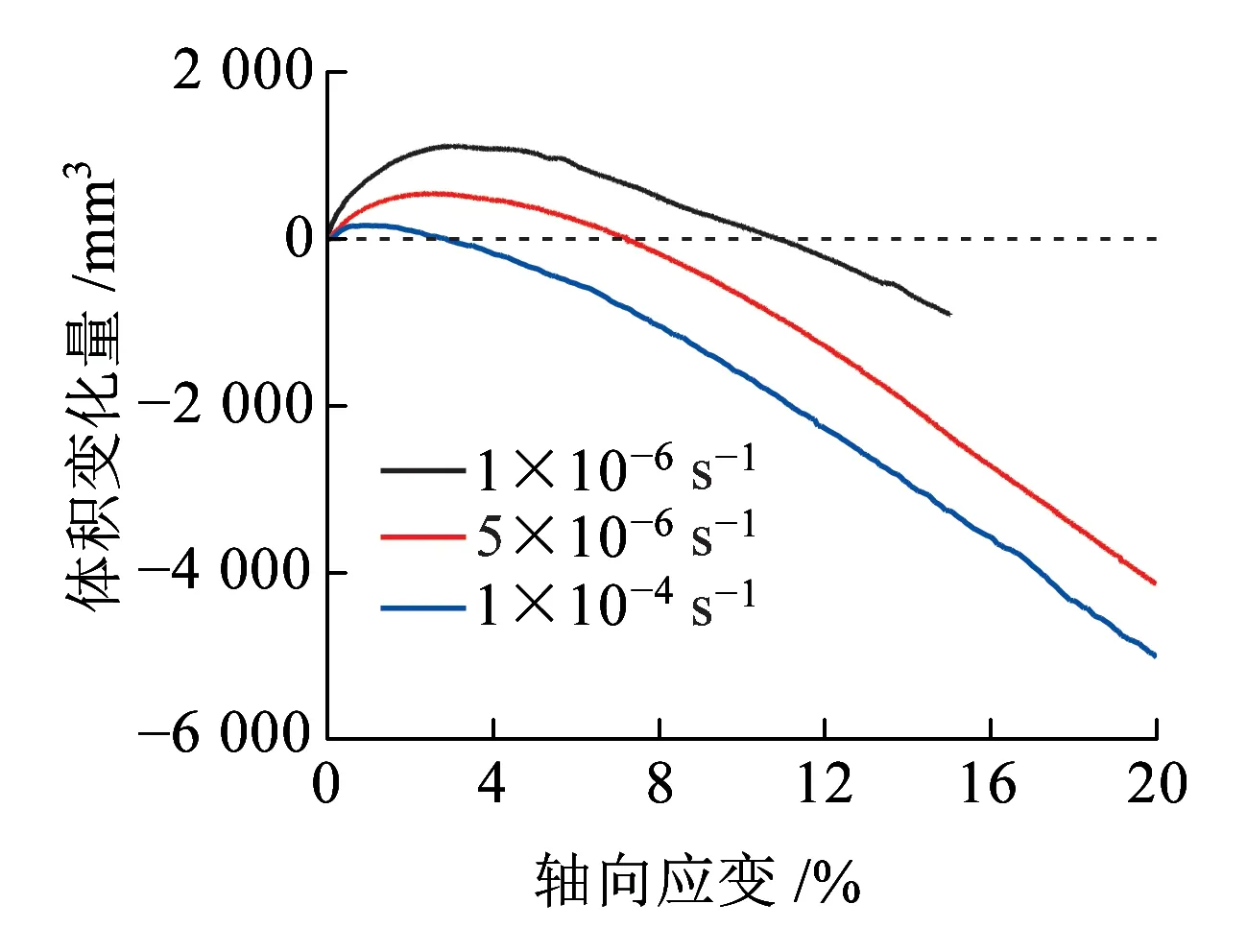
图8 围压150 kPa下试样的体积变化量-应变曲线

土骨架黏滞性效应和固结效应在试样变形过程中是同时存在的，两者难以量化分离。但是，黏滞性和固结效应分别与应变速率呈正相关和负相关。因此，图4中低应变速率和高应变速率对应的强度变化率峰值分别是固结效应和黏滞性效应主要作用的结果。高、低应变速率对应的强度变化率峰值与围压的关系如图9所示。从图9可以看出，低应变速率对应的强度变化率峰值随围压的增加近似线性增大，高应变速率对应的强度变化率峰值则随之减小。因此，高围压和低应变速率有利于固结作用比例的增大，而低围压和高应变速率则有利于黏滞性作用比例的增大。

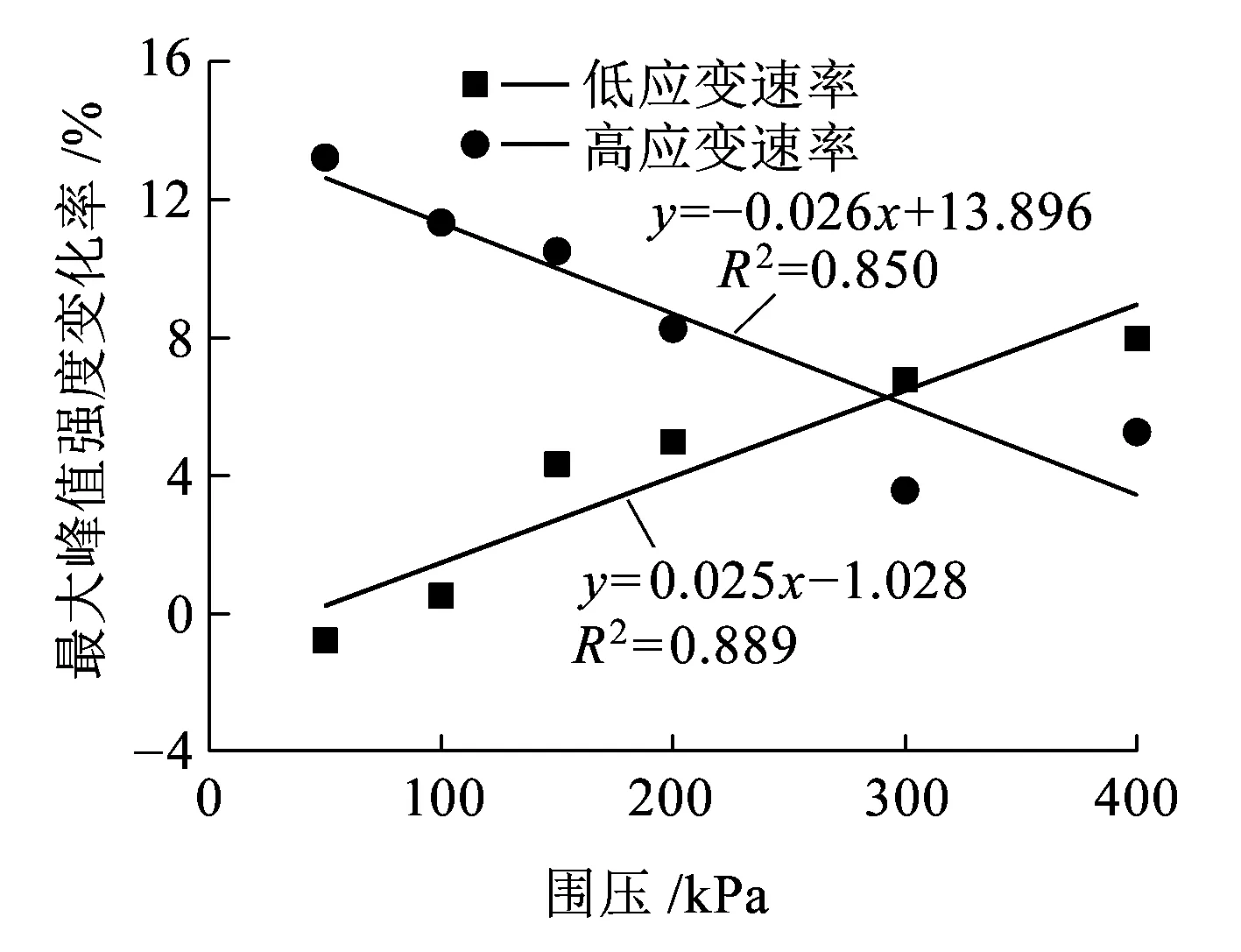
图9 高、低应变速率对应的强度变化率峰值-围压关系曲线

上述现象的原因在于，低围压时外部荷载主要由土骨架承担，颗粒间胶结作用抑制了孔隙水压力和气压力的产生；而高围压下，孔隙压力传递的阻力减小，有利于水、气运移。在高围压和低应变速率条件下，土体孔隙中空气和自由水承担的荷载有充足的时间转移到土骨架上，试样内部孔隙的水、气向表层运动，土颗粒间距和结合水膜厚度随之减小，从而增强了颗粒间连接力。因此，在低应变速率时，由于固结效应的主导作用，土体变形和强度指标随应变速率的增加逐渐减小；同时，随着应变速率的增加和固结效应的减弱，黏滞性效应开始起主导作用，土体变形和强度指标值转而逐渐增大。

3.3 孔隙压力的应变速率效应

对于弱透水性的粉质黏土，围压较小时，应变速率对孔隙压力的影响较小；应变速率和围压较大时，孔隙水、气来不及运移和消散，加载时只是孔隙气的压密以及部分气体溶解于孔隙水中，从而产生超过加载前的孔隙水压力增量和孔隙气压力增量，即超孔隙压力。超孔隙压力会抵消部分围压，降低基质吸力，进而引起强度的减小，即超孔隙压力效应[27-29]。

当饱和度较高时，土体对外部荷载和环境的响应特征与饱和土具有一定相似性[1]。同时，由于非饱和土孔隙压力量测的复杂性，大范围的孔隙水压力和气压力量测仍存在一定困难[28]。本文试样饱和度为78.1%，属于高饱和度土，因此通过相同压实度饱和试样的不排水三轴试验结果对本文试样孔隙压力的应变速率特征进行分析，结果见表4、表5。从表4、表5可以看出，在应变速率1×10-4～1×10-3s-1范围内，围压为100 kPa时，饱和试样的峰值强度逐渐增大；围压为300 kPa时，峰值强度则逐渐减小，与非饱和试样的变化规律一致。同时，峰值强度对应的孔隙水压力随应变速率均呈逐渐增大的规律，且高围压时孔隙水压力的增大比例比低围压时大，因此高围压和高应变速率会增强超孔隙压力的作用程度。

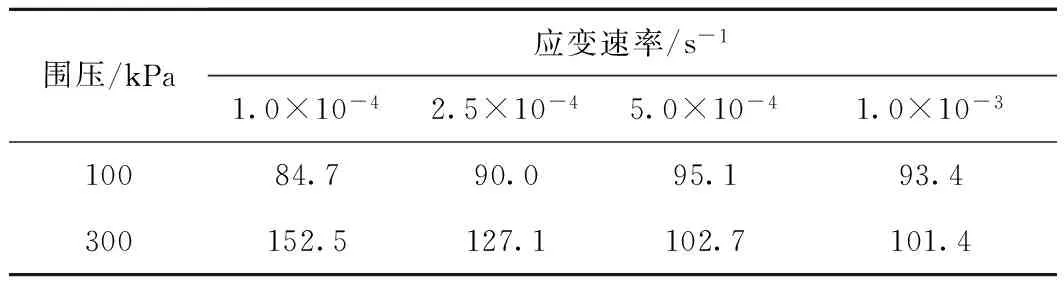
表4 饱和试样峰值强度S统计

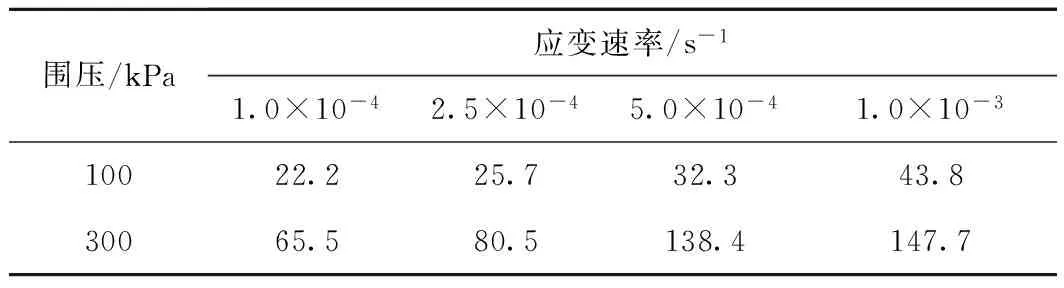
表5 饱和试样孔隙水压力u统计

此外，由于土体的结构性特征，应力和应变在应变速率过大时来不及调整，也容易形成应力应变的集中现象，因此，综合导致围压和应变速率较大时的峰值强度出现一定程度的降低(图4(b))，对应的峰值应变也明显减小(图6)。

综上所述，非饱和土的应变速率效应是围压和偏应力引起的固结效应、土骨架本身的黏滞效应，以及孔隙压力等因素共同作用的结果。同时，各因素作用比例会受到围压、应变速率及土性等条件的综合影响。高围压和低应变速率有利于固结的进行，低围压和高应变速率有利于黏滞性的体现，高围压和高应变速率有利于超孔隙压力的产生，由此使得土体强度特性随应变速率和围压的变化出现多种变化规律。

4 结论

(1)应变速率对粉质黏土的应力-应变曲线形态有明显影响。在低围压下，高应变速率有助于应变软化现象的出现。随着应变速率的减小或围压的增大，应力-应变曲线逐渐向应变硬化型过渡，同时应变速率的影响程度逐渐降低。相应地，在低围压下，试样破坏时有明显的剪切破裂面，随着应变速率的减小，剪切面位置下降，破坏程度逐渐降低。随着围压的增大，破裂面逐渐消失，试样呈塑性鼓胀破坏形式。

(2)随着应变速率的增加，峰值强度在低围压下呈先减小、后增大的规律；在高围压下则呈先减小、后增大、再减小的规律，且高围压可以降低应变速率对峰值强度的影响程度。存在两类应变速率临界值使峰值强度的变化趋势有所不同，其中第二类临界值仅在高围压下出现，且临界值均随围压的增加而增大。当实际应变速率低于《土工试验方法标准》[20]建议值时，低围压下的试验值一般大于实际值，高围压下的试验值则一般小于实际值。峰值应变随应变速率的增加而减小，同时其变化幅度随围压的增加而降低。弹性模量在低围压下随应变速率逐渐增大，在高围压下则先减小、后增大。

(3)粉质黏土的应变速率效应受到围压和偏应力作用下的固结、土骨架黏滞性及孔隙压力等因素的综合影响。各因素作用的比例关系随围压和应变速率的变化也有所不同，高围压和低应变速率有利于固结的进行，低围压和高应变速率有利于黏滞性作用比例的增大，高围压和高应变速率有利于超孔隙压力作用的发挥，由此会引起不同的应变速率效应。

(4)对于不同的路基填料类型，有必要针对围压水平和应变速率校正其变形和强度指标的设计取值。可以采用线性函数拟合粉质黏土峰值强度、峰值应变与应变速率的关系，及两类应变速率临界值与围压的关系。弹性模量与应变速率的关系则可采用二次多项式描述。

以上结论可为增大路基围压、合理控制列车轴重及车速等工作提供参考，也可为满足线路运营中列车轴重及车速等条件合理确定路基材料、围压等设计要求提供依据。

参考文献：

[1]JAMES K M,KENICHI S.Fundamentals of Soil Behavior[M].New York City:John Wiley & Sons,2005.

[2]何菲,王旭,刘德仁,等.青藏铁路原状冻结砂土动力特性参数试验研究[J].铁道学报,2017,39(6):112-117.

HE Fei,WANG Xu,LIU Deren,et al.Experimental Study on Dynamic Characteristic Parameters of Undisturbed Frozen Sandy Soil of Qinghai-Tibet Railway[J].Journal of the China Railway Society,2017,39(6):112-117.

[3]王青志,朱鑫鑫,刘建坤,等.寒区高速铁路路基粗颗粒填料大型直剪试验研究[J].铁道学报,2016,38(8):102-109.

WANG Qingzhi,ZHU Xinxin,LIU Jiankun,et al.Experimental Study on Direct Shear Tests of Coarse-gained Fillings of High-speed Railway Subgrade in Cold Region[J].Journal of the China Railway Society,2016,38(8):102-109.

[4]朱启银,尹振宇,朱俊高,等.软黏土加载速率效应特性试验研究:进展与趋势[J].岩土力学,2014,35(1):7-24.

ZHU Qiyin,YIN Zhenyu,ZHU Jungao,et al.Progress and Trend of Experimental Investigation on Rate-dependent Behavior of Soft Clays[J].Rock and Soil Mechanics,2014,35(1):7-24.

[5]YAMAMURO J A,LADE P V.Effects of Strain Rate on Instability of Granular Soils[J].International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts,1994,31(2):A66.

[6]ZHU J G,YIN J H.Strain-rate-dependent Stress-strain Behavior of Over-consolidated Hong Kong Marine Clay[J].Canadian Geotechnical Journal,2000,37(6):1272-1282.

[7]SHEAHAN T.An Experiment Study of the Time-dependent Undrained Shear Behavior of Resedimented Clay Using Automated Stress Path Triaxial Equipment[D].Cambridge:Massachusetts Institute of Technology,1991.

[8]姜洪伟,赵锡宏.剪切速率对各向异性不排水剪强度影响分析[J].同济大学学报,1997,25(4):390-395.

JIANG Hongwei,ZHAO Xihong.Analysis of the Shearing Rate Effect on Anisotropic Undrained Strength of Clays[J].Journal of Tongji University,1997,25(4):390-395.

[9]高彦斌,汪中为.应变速率对粘土不排水抗剪强度的影响[J].岩石力学与工程学报,2005,24(S2):5779-5783.

GAO Yanbin,WANG Zhongwei.Effect of Strain Rate on Undrained Shear Strength of Clays[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(S2):5779-5783.

[10]陈铁林,周成,沈珠江.结构性黏土压缩和剪切特性试验研究[J].岩土工程学报,2004,26(1):31-35.

CHEN Tielin,ZHOU Cheng,SHEN Zhujiang.Compression and Shear Test of Structured Clay[J].Chinese Journal of Geotechnical Engineering,2004,26(1):31-35.

[11]党进谦,蒋仓兰,吉中亮.剪切速率对结构性黄土力学性状的影响[J].地下空间与工程学报,2009,5(3):459-462.

DANG Jinqian,JIANG Canglan,JI Zhongliang.Effects of Shear Rate on Mechanical Behavior of Structured Loess[J].Chinese Journal of Underground Space and Engineering,2009,5(3):459-462.

[12]邓亚虹,魏宝华,王晗,等.原状黄土变形与强度特性的加载速率效应[J].中国公路学报,2016,29(7):22-29.

DENG Yahong,WEI Baohua,WANG Han,et al.Loading Rate Effect on Deformation and Strength Characteristics of Undisturbed Loess[J].China Journal of Highway and Transport,2016,29(7):22-29.

[13]蔡羽,孔令伟,郭爱国,等.剪应变率对湛江强结构性黏土力学性状的影响[J].岩土力学,2006,27(8):1235-1240.

CAI Yu,KONG Lingwei,GUO Aiguo,et al.Effects of Shear Strain Rate on Mechanical Behavior of Zhanjiang Strong Structured Clay[J].Rock and Soil Mechanics,2006,27(8):1235-1240.

[14]SHEAHAN T C,LADD C C,GERMAINE J T.Rate-dependent Undrained Shear Behavior of Saturated Clay[J].Journal of Geotechnical Engineering,ASCE,1996,122 (2):99-108.

[15]但汉波,王立忠.K0固结软黏土的应变率效应研究[J].岩土工程学报,2008,30(5):718-725.

DAN Hanbo,WANG Lizhong.Strain-rate Dependent Behaviors ofK0Consolidated Clays[J].Chinese Journal of Geotechnical Engineering,2008,30(5):718-725.

[16]TATSUOKA F,BENEDETTO H D,ENOMOTO T,et al.Various Viscosity Types of Geomaterials in Shear and Their Mathematical Expression[J].Soils and Foundations,2008,48(1):41-60.

[17]周杰,周国庆,赵光思,等.高应力下剪切速率对砂土抗剪强度影响研究[J].岩土力学,2010,31(9):2805-2810.

ZHOU Jie,ZHOU Guoqing,ZHAO Guangsi,et al.Analysis of Influence of Shear Rate on Shear Strength of Sand under High Stress[J].Rock and Soil Mechanics,2010,31(9):2805-2810.

[18]ZHANG Y,ISHIKAWA T,TOKORO T,et al.Influences of Degree of Saturation and Strain Rate on Strength Cha-racteristics of Unsaturated Granular Subbase Course Material[J].Transportation Geotechnics,2014(1):74-89.

[19]周科峰,李宇峙.考虑加载速率的级配碎石三轴压缩强度特性[J].中南大学学报:自然科学版,2015,46(7):2613-2619.

ZHOU Kefeng,LI Yuzhi.Characteristic of Triaxial Compressive Strength of Grading Macadam Considering Loading Velocity[J].Journal of Central South University:Science and Technology,2015,46(7):2613-2619.

[20]国家质量技术监督局,中华人民共和国建设部.GB/T 50123—1999 土工试验方法标准[S].北京:中国计划出版社,1999.

[21]KABBAJ M,TAVENAS F,LEROUEIL S.In-situ and Laboratory Stress-strain Relationships[J].Géotechnique,1988,38(1):83-100.

[22]王智超,罗迎社,罗文波,等.路基压实土流变变形的力学表征及参数辨识[J].岩石力学与工程学报,2011,30(1):208-216.

WANG Zhichao,LUO Yingshe,LUO Wenbo,et al.Mechanical Charaterization and Parameter Identification of Rheological Deformation of Subgrade Compacted Soil[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(1):208-216.

[23]TATSUOKA F,ISHIHARA M,BENEDETTO H D,et al.Time-dependent Shear Deformation Characteristics of Geomaterials and Their Simulation[J].Soils and Foundations,2002,42(2):103-129.

[24]张先伟,王常明.结构性软土的黏滞系数[J].岩土力学,2011,32(11):3276-3282.

ZHANG Xianwei,WANG Changming.Viscosity Coefficient of Structural Soft Clay[J].Rock and Soil Mechanics,2011,32(11):3276-3282.

[25]张志红,赵成刚,邓敏.非饱和土固结理论新进展[J].岩土力学,2005,26(4):667-672.

ZHANG Zhihong,ZHAO Chenggang,DENG Min.Recent Development of Consolidation Theories of Unsaturated Soils[J].Rock and Soil Mechanics,2005,26(4):667-672.

[26]American Society for Testing Materials.Annual Book of ASTM Standards[S].2003.

[27]WHEELER S J,SHARMA R S,BUISSON M S R.Coup-ling of Hydraulic Hysteresis and Stress-strain Behaviour in Unsaturated Soils[J].Géotechnique,2003,53(1):41-54.

[28]李广信.静孔隙水压力与超静孔隙水压力:兼与陈愈炯先生讨论[J].岩土工程学报,2012,34(5):957-960.

LI Guangxin.Static Pore Water Pressure and Excess Pore Water Pressure:A discussion with Mr CHEN Yujiong[J].Chinese Journal of Geotechnical Engineering,2012,34(5):957-960.

[29]卢宁,LIKOS W J.非饱和土力学[M].韦昌富,侯龙,简文星,译.北京:高等教育出版社,2012.