城市轨道交通乘客半补偿路径选择建模与应用

张永生，姚恩建，刘莎莎，蔡昌俊，2

(1.北京交通大学 交通运输学院，北京 100044； 2.广州地铁集团有限公司，广东 广州 510310)

在城市轨道交通网络中，换乘站衔接了不同的线路，使得乘客的备选路径往往不止一条。城轨乘客路径选择模型通过综合考量多种因素以确定各路径的选择比例，进而估算换乘量、断面流量、线路流量等，为线路规划、客流组织、运行计划编制、票务清分等业务提供数据支撑。尤其当新线接入等导致路网结构发生变化时，基于刷卡数据的清分模型[1-3]等数据驱动方法难以应用，而基于离散选择理论的路径选择模型是从乘客的行为解释角度出发，揭示不同因素对乘客的影响程度，因此，该模型可以应用到网络结构发生变化后的场景中。

目前，基于离散选择理论的路径选择模型主要以Multinomial Logit(MNL)模型[4]及其衍生模型为主。在轨道交通路径选择行为分析方面，文献[5-10]分别从模型的应用推广、模型的理论演化和不同数据源下模型推导等不同角度进行了尝试，充分证明了该类模型的优越性。文献[11-15]逐渐增加了地铁服务水平、个体属性、出行目的、路网拓扑结构等因素对城轨乘客路径选择偏好的影响分析，从行为学角度完善了模型的可解释性。

基于离散选择理论的路径选择模型利用微观经济学和行为学诠释了出行者实际的决策过程。通过综合权衡各因素的优劣，出行者从有效路径集合中挑选出感知效用最大的路径。这是一个半补偿的过程，即有效路径集合生成(非补偿)与路径择优(补偿)的结合[16]。非补偿表示有效的路径不能超过某因素(如：时间)的容忍阈值；补偿表示考虑各因素的综合效果，从所有有效的路径中选出最优的路径。但既有研究中，有效路径集合的判断阈值大都根据主观经验或其他调查数据外生标定，导致阈值与乘客的选择行为脱节。即在当前城市轨道交通的乘客路径选择建模方面，学者们大都只关注补偿性的各影响因素间相互替代关系的求解和应用，而忽视了非补偿性的有效路径集合阈值的合理估算及它们之间的内在关联性。

本文构建城轨乘客半补偿Mixed Logit(ML)路径选择模型，一方面内生性地求解各影响因素的系数和有效路径集合阈值，解析城轨乘客路径选择的半补偿过程，另一方面以ML模型结构[17]防止MNL模型选择肢间独立不相关的假设的影响，准确反映不同乘客间的差异性(异质性)，包括补偿性选择过程的差异性和非补偿性有效路径集合构造过程中乘客容忍阈值的差异性。考虑到所建模型结构的相对复杂性，将马尔科夫链蒙特卡洛法与数据扩张技术进行融合，搭建出参数估算方法。以在广州地铁得到的调查数据，对所建模型进行标定，并对其在新线接入条件下的预测性能进行分析。

1 城轨乘客半补偿ML路径选择模型

1.1 城轨乘客路径选择的半补偿性与异质性体现

图1是基于2013年7月在广州地铁进行问卷调查得到的统计结果(共14 142个样本)。图1(a)描述的是若最短出行时间为30 min，乘客可容忍的最长出行时间(预设6个选项供被调查者选择1项)；图1(b)统计的是最少换乘次数为0次时，乘客对容忍阈值选择的结果。上述结果说明乘客对路径的出行时间和换乘次数都有一定的容忍限制，即有效路径集合是满足一定限制条件的路径的集合。同时，不同阈值形成不同的有效路径集合将导致不同的模型估计结果，即阈值参数与效用函数系数有内在关联性，外生估计的阈值将导致有偏的效用函数系数，不能准确反映城轨乘客的路径选择行为。上述现象体现了半补偿性对城轨乘客路径行为的影响。而且，图1还显示出乘客在阈值上的差异性。因此，本文将阈值设置为随机变量，以体现乘客对阈值的异质性，并联立非补偿性的有效路径集合构造和补偿性的路径选择两个过程，内生地估计效用函数和阈值的各参数。

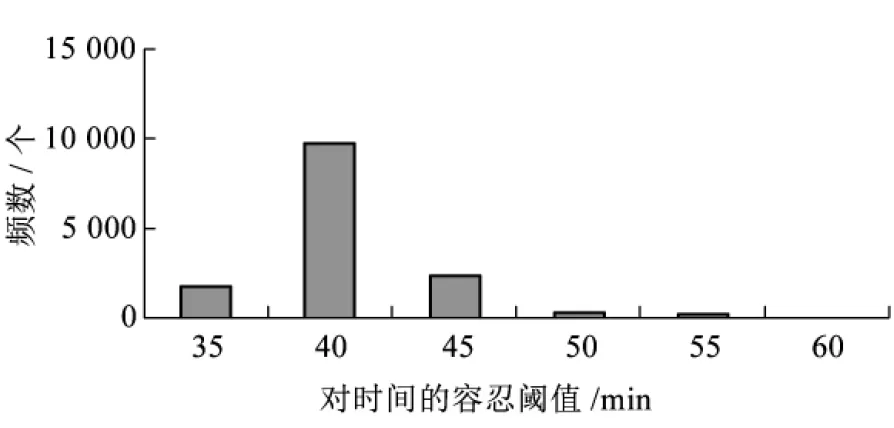
(a)时间容忍阈值分布(相对于30 min)

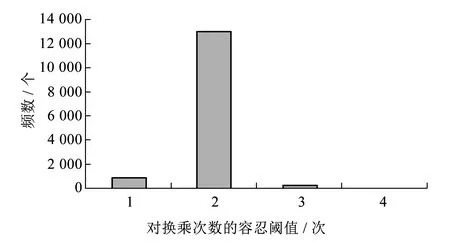
(b)换乘次数的容忍阈值分布(相对于0次)图1 容忍阈值例证

1.2 城轨乘客半补偿路径选择模型

考虑到有效路径集合生成过程和路径选择过程的先后顺序，基于贝叶斯理论，以有效路径集合的选择为先验知识，构造半补偿选择模型。

( 1 )

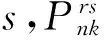
1.3 非补偿性选择部分

( 2 )

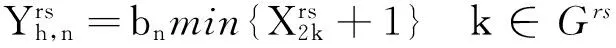
( 3 )

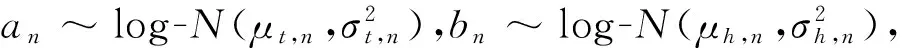
( 4 )

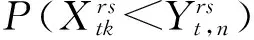
( 5 )

( 6 )

在成网条件下，城市轨道交通中同一OD对间的路径条数是很多的，通过任意组合，有效路径集合的数量更是庞大，为节省计算时间，同时考虑到大多数路径被考虑的概率基本为0，因此路径总集合Grs一般设置为有可能被选择到的路径的集合。考虑到目前城市轨道交通路网的规模，本文分别以最短出行时间和最少换乘次数为标准各取前3条路径，即同一OD对间的路径总集合Grs最多有6条不同路径，有效路径集合的个数最多为63个。

1.4 补偿性选择部分

基于随机效用理论，对于出行者n而言，从起点r到终点s的第k条路径的随机效用为

( 7 )

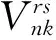
为体现乘客在补偿性选择过程中的差异性，同时避免MNL模型选择肢独立不相关假设的影响，本文构造了Mixed Logit路径选择模型，该模型假设特征变量参数为随机变量。

( 8 )

( 9 )

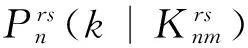
换乘次数与乘车时间的量纲不同，为对比两者对乘客路径选择偏好的影响，利用“等效乘车时间系数”[14]将换乘次数转化为等车时间。

2 半补偿ML路径选择模型求解算法

2.1 参数选择

各参数的随机分布形式一般包括均匀分布、对数正态分布、正态分布、SB分布和三角分布等[17]。考虑到参数符号的意义和参数估算难度，本文将分别基于对数正态分布、正态分布和固定值等三种形式进行参数估算，选择出最优结果。

2.2 参数估计

鉴于参数估计时积分运算的复杂性，本文通过融合马尔科夫链蒙特卡洛法与数据扩张技术[18]，估算参数，步骤如下：

设未知参数为θ=(μY，σY，μβ，σβ)，其中(μY，σY)为阈值参数的分布参数；(μβ，σβ)为特征变量参数β的分布参数。

步骤1随机产生参数θl。当l=0时，θl=0；当l≥1时，基于θl～N(θl-1，σ)(其中σ根据参数范围设定为常数)获得随机参数θl，并基于θl中的特征变量参数的分布参数获得一组随机值βl。

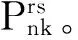
步骤3计算似然函数。改造的似然函数为

P(βl|(μβ l，σβ l))

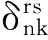
步骤4令λ=ln(Ll)-ln(Ll-1)，并进行如下判断：当λ≥0时，θl=θl；当λ<0时，产生服从U(0，1)的随机数τ，当λ≥ln(τ)，θl=θl，否则θl=θl-1，Ll=Ll-1。

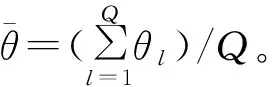
上述参数估算方法主要依托于SP(StatedPreference)或RP(RevealedPreference)调查数据。通过调查获得乘客对路径的选择结果，以此估算乘客路径选择时的行为偏好参数。本文所建模型从行为解释角度挖掘了各种因素对乘客路径选择的影响程度，该影响程度在短期内(如3～5年)一般不会发生明显变化，也不会随着路网的扩张而变，因此所标定的参数在短期内应用时，无需重新标定或调整，适用于日益复杂的轨道交通运营环境。

3 实例分析

3.1 数据基础

2013年年底广州地铁开通六号线，该线路自西向东，穿过市区，与既有线路形成了7个换乘站，路网结构发生较大变化。本文基于六号线开通之前的调查数据标定模型，分析模型的统计效果，预测六号线开通后的路径选择比例，检验所建模型在应用时的预测性能。所用调查数据来源于2013年7月针对广州地铁乘客出行特征的调查，主要包括个体属性、乘客此次出行实际选择的路径、乘客对时间和换乘次数的容忍阈值等信息，有效样本量为14 142份。

3.2 模型标定结果

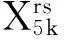
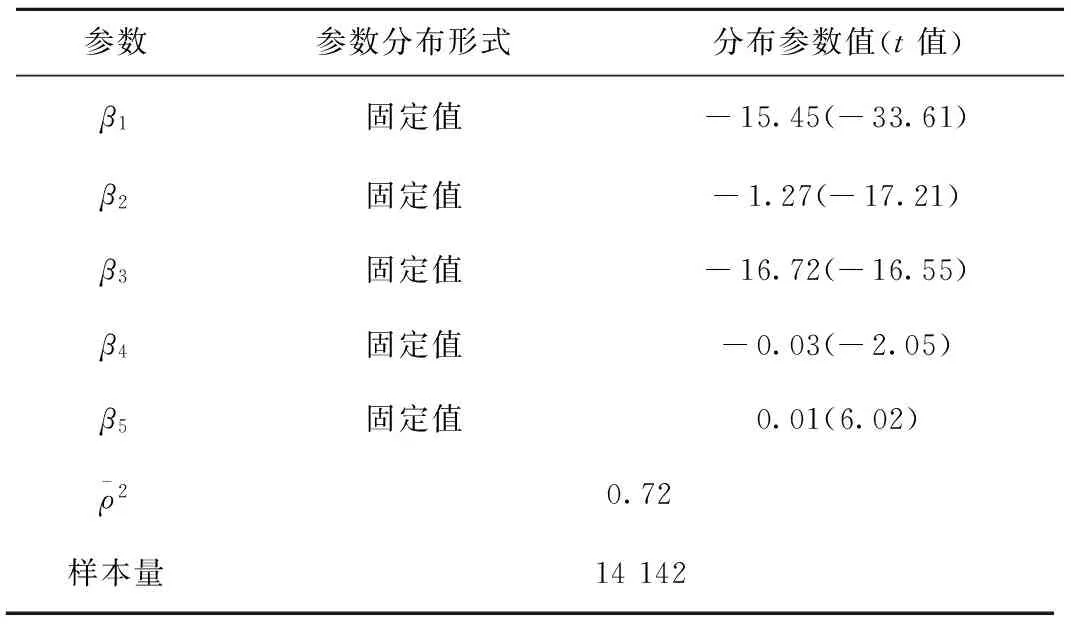
表1 MNL路径选择模型参数标定结果

表2 ML路径选择模型参数标定结果

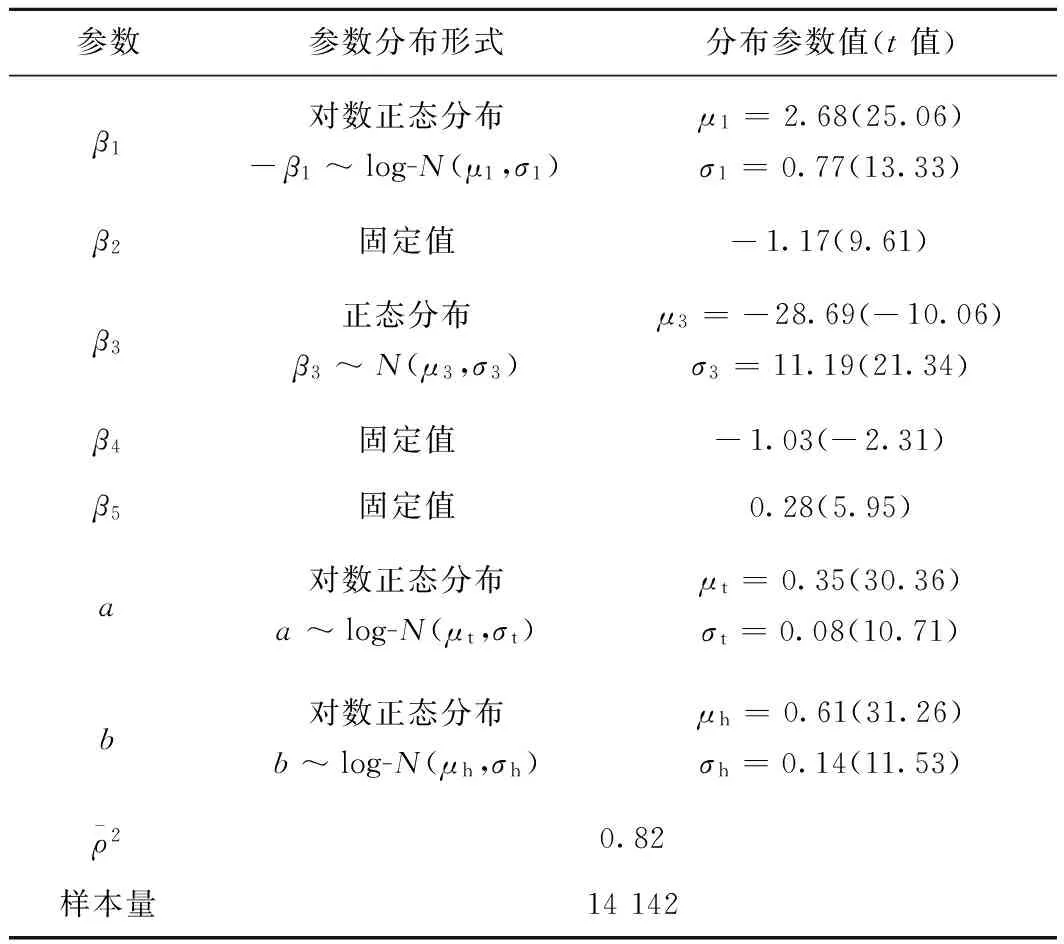
表3 半补偿ML路径选择模型参数标定结果

分析以上3个表中的数据，可得到以下结论：

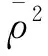
(2)乘车时间、换乘次数、换乘时间以及角度费用的系数取值为负数，表示乘客更倾向于选择时间短、费用低、换乘次数少的路径。舒适程度的系数为正值，表示乘客倾向于选择更舒适的路径。

(3)在表2和表3中，换乘时间的系数服从于正态分布，虽然会出现换乘时间的系数为正的缺点，但其所占比例分别仅为Φ(-29.4/10.89)=0.35%，Φ(-28.69/11.19)=0.52%，可以忽略不计。

进一步观察，表3中的出行时间和换乘次数阈值参数均服从于对数正态分布。其中，出行时间阈值参数a的数学期望为1.42，方差为0.01，即平均来讲，超过最短出行时间1.42倍的路径，不会被乘客考虑；换乘次数阈值参数b的数学期望为1.86，方差为0.07，即平均来讲，令最少换乘次数加1次，超过该值1.86倍的路径，不会被乘客考虑。对比图1的调查结果，乘客对30 min的容忍阈值的均值为40.5 min，而标定结果1.42×30=42.6 min；乘客对换乘0次的容忍阈值的均值为1.95次，而标定结果为1.86×(0+1)=1.86次。结果说明标定结果符合实际，更精准(调查结果为离散值，其均值并不精准)。

而且，为对比乘车时间和换乘次数对城轨乘客路径选择偏好的影响，可进行等效乘车时间分析。由于-β1～log-N(μ1，σ1)，则ln(-β1)～N(μ1，σ1)，进而ln(β2/β1)=[ln(-β2)-ln(-β1)]，因此可得到ln(β2/β1)～N(ln(-β2)-μ1，σ1)，即β2/β1为对数正态分布，β2/β1～log-N(ln(-β2)-μ1，σ1)。换乘次数的等效乘车时间系数的单位为h/次，该值较小，为便于描述，将等效乘车时间系数的单位调为min/次，即60·β2/β1～log-N(ln(-60·β2)-μ1，σ1)，如图2所示，其数学期望值为6.6 min/次，即换乘1次相当于乘车时间6.6 min。

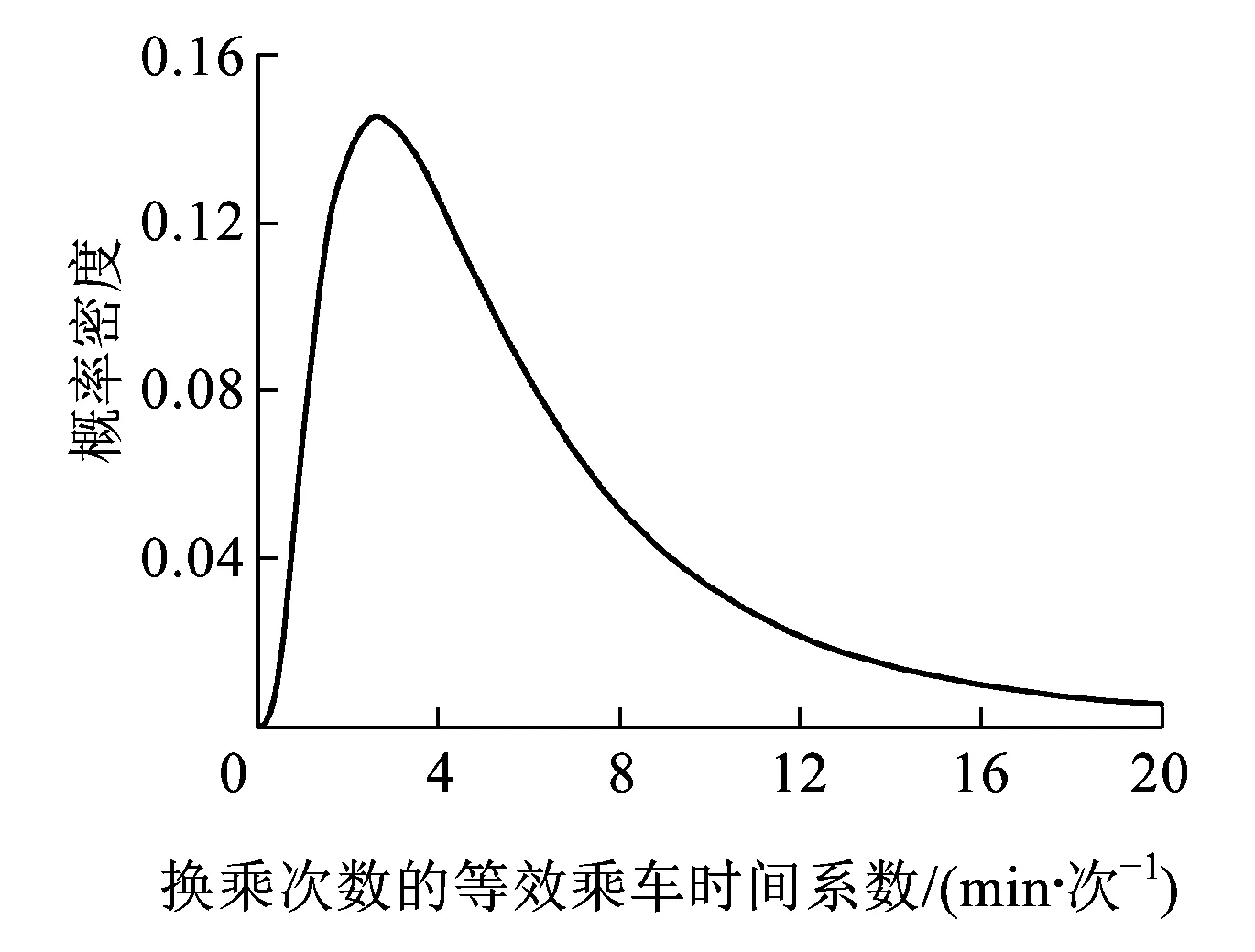
图2 换乘次数的等效乘车时间系数对数正态分布概率密度图

3.3 模型应用

换乘量预测值是进行换乘站设计和换乘客流组织预案编制的基础。本文通过路径选择模型预测换乘量，一方面可体现路径选择模型的应用价值，另一方面可用来校验所建模型的预测效果。在实际应用中，需首先确定路径总集合和各影响因素的取值，进而基于标定的路径选择模型计算站点间各条路径的选择比例，结合站点间客流量，统计换乘量。模型应用时各变量的取值原则与模型标定时类似，其中，运营管理部门可提供预计的列车运行计划、换乘走行时间和满载率(新路段的满载率初始值为0)。本文以上述六号线开通前的调查结果标定的模型为基础，利用广州地铁集团有限公司提供的2014年3月(六号线开通后)的路网数据、列车运行计划、满载率与换乘走行时间，分别以最短出行时间和最少换乘次数为标准各取前3条路径组成路径总集合，并计算出各条路径各变量的取值，进而基于式( 1 )判断每个时间窗(此处以15 min为一个时间窗)下路径总集合中各条路径的选择比例，乘以对应时间窗下站点间客流量，通过统计得到预测的六号线开通后的各换乘站各换乘流向(如：十字交叉式的换乘站共有8个换乘流向)全天换乘量(共19个换乘站，138个换乘流向)，详见文献[14]的描述，并以广州地铁集团有限公司提供的清分结果为校验值。如图3所示，纵轴为预测值，横轴为校验值，数据点围绕在45°线附近，说明预测值接近于校验值。经计算，平均相对误差为5.19%，满足运营管理部门的业务需求。

图3 全天换乘量预测校验45°线图

4 结论

路径选择过程是有效路径集合生成和路径择优两个过程的统一，同时乘客间的差异性不仅表现在选择偏好的差异，还表现在有效路径集合阈值的差异。本文针对既有研究对上述两个过程的孤立和对乘客间异质性的考量不足等缺点，构建城轨乘客半补偿ML路径选择模型，不仅将上述两个过程统一为整体，实现了效用函数参数和阈值的内生标定，还充分考虑了乘客间的异质性。基于RP调查数据对模型进行标定，可以得到如下结论：

(1)所建半补偿ML模型在拟合效果和预测效果上均优于一般的MNL模型和ML模型。

(2)换乘时间的等效乘车时间系数为对数正态分布。经计算，数学期望为6.6 min/次，表明平均来讲，换乘1次相当于乘车6.6 min。

(3)出行时间和换乘次数阈值均服从于对数正态分布，根据其期望值对比实际调查结果，证实了标定结果的合理性。

本文探讨了所建模型的应用效果，针对广州地铁六号线接入导致路网结构发生巨大变化的场景，预测了各换乘站换乘量，对比校验值，平均相对误差为5.19%，证明所建模型可以较好地适应网络结构变化条件下的客流预测。

参考文献：

[1]SUN Y,XU R.Rail Transit Travel Time Reliability and Estimation of Passenger Route Choice Behavior[J].Transportation Research Record,2012,2275(1):58-67.

[2]ZHOU F,SHI J,XU R.Estimation Method of Path-selecting Proportion for Urban Rail Transit Based on AFC Data[J].Mathematical Problems in Engineering,2015,2015(6):1-9.

[3]SUN L,JIN J,LEE D H,et al.Characterizing Travel Time Reliability and Passenger Path Choice in a Metro Network[C]//Proceedings of Transportation Research Board-94th Annual Meeting.Washington D C:TRB Publisher,2015:1-16.

[4]MCFADDEN D.The Revealed Preferences of Government Bureaucracy[J].The Bell Journal of Economics,1975,6(2):401-416.

[5]YAO E,MORIKAWA T.A Study on Integrated Intercity Travel Demand Model[J].Transportation Research Part A:Policy and Practice,2005,39(4):367-381.

[6]DAAMEN W,BOVV P H L,HOOGENDOOM S P,et al.Passenger Route Choice Concerning Level Changes in Railway Stations[C]//Proceedings of Transportation Research Board-84th Annual Meeting.Washington D C:TRB Publisher,2005:1-18.

[7]四兵锋,毛保华,刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法[J].铁道学报,2007,29(6):12-18.

SI Bingfeng,MAO Baohua,LIU Zhili.Passenger Flow Assignment Model for Urban Railway Traffic Network under the Condition of Seamless Exchange[J].Journal of the China Railway Society,2007,29(6):12-18.

[8]徐瑞华,罗钦,高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究[J].2009,31(2):110-114.

XU Ruihua,LUO Qin,GAO Peng.Passenger Flow Distribution Model and Algorithm for Urban Rail Transit Network Based on Multi-route Choice[J].Journal of the China Railway Society,2009,31(2):110-114.

[9]刘剑锋,孙福亮,柏赟,等.城市轨道交通乘客路径选择模型及算法[J].交通运输系统工程与信息,2009,9(2):85-90.

LIU Jianfeng,SUN Fuliang,BAI Yun,et al.Passenger Flow Route Assignment Model and Algorithm for Urban Rail Transit Network[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(2):85-90.

[10]SUN L,LU Y,JIN J,et al.An Integrated Bayesian Approach for Passenger Flow Assignment in Metro Networks[J].Transportation Research Part C:Emerging Technologies,2015,52(1):116-131.

[11]RAMMING M S.Network Knowledge and Route Choice[D].Massachusetts:Massachusetts Institute of Technology,2001:111-212.

[12]SEBASTIAN R,MUNOZ J C,GRANGE L D.A Topological Route Choice Model for Metro[J].Transportation Research Part A:Policy and Practice,2011,45(2):138-147.

[13]SEBASTIAN R,ZHAN G,JUAN C M,et al.A Behavioral Comparison of Route Choice on Metro Networks:Time,Transfers,Crowding,Topology and Socio-demographics[J].Transportation Research Part A:Policy and Practice,2014,66(1):185-195.

[14]张永生,姚恩建,代洪娜.成网条件下地铁换乘量预测方法研究[J].铁道学报,2013,35(11):1-6.

ZHANG Yongsheng,YAO Enjian,DAI Hongna.Transfer Volume Forecasting Method for the Metro in Networking Conditions[J].Journal of the China Railway Society,2013,35(11):1-6.

[15]刘莎莎,姚恩建,张永生.轨道交通乘客个性化出行路径规划算法[J].交通运输系统工程与信息,2014,14(5):100-104.

LIU Shasha,YAO Enjian,ZHANG Yongsheng.Personalized Route Planning Algorithm for Urban Rail Transit Passengers[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(5):100-104.

[16]BEN-AKIVA M E,BOCCARA B.Discrete Choice Models with Latent Choice Sets[J].International Journal of Research in Marketing,1995,12(1):9-24.

[17]MCFADDEN D,TRAIN K.Mixed MNL Models for Discrete Response[J].Journal of Applied Econometrics,2000,15(5):447-470.

[18]DAVID A D,MENG X.The Art of Data Augmentation[J].Journal of Computational and Graphical Statistics,2001,10(1):1-50.