砾石冲击下动车组裙板的变形影响因素分析

姜 成，姚曙光，曹武雄，彭 勇，张 健

(1.中南大学 交通运输工程学院，湖南 长沙 410075；2.中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075)

截至2016年底，我国已经开通运营高速铁路线路2.2万km，其中有砟轨道铁路线路占有一定的比例[1]。随着高速列车运行速度的不断提升，高速铁路有砟轨道上的道砟、砂石、冰粒等物体会在强大的列车风力作用下发生飞溅，击打线路设备、列车车下设备舱、列车走行部等处，严重时会危及行车安全。客运专线京哈线秦沈段，开通时列车运行速度达到250 km/h，列车高速运行时出现列车风造成道砟飞溅、击打列车车下设备等事故[2-4]。严寒地区在冬天下雪情况下，当列车速度达到250 km/h时，强大的列车风在带动冰雪飞溅的同时还会引起道砟砾石颗粒飞溅[5-8]。文献[9-10]对高速铁路道砟飞溅现象进行系统分析和风险评估，研究表明相邻列车以低于160 km/h速度交会时，也会导致道砟飞溅。文献[11-12]研究表明，列车转向架结构会使高速行驶列车底部产生瞬间高强湍流流场造成道床表面道砟飞溅现象。高速列车的牵引系统设备、用电设备等大部分关键设备都吊装在全封闭的车下设备舱内，设备舱裙板在改善动车组空气动力学外形、保护车下悬挂设备等方面起着关键作用，其结构抗冲击性能对动车组的安全运营至关重要[13]。可见道砟、砂石冲击列车车下设备是一个亟待解决的影响行车安全的工程问题。因此，动车组裙板冲击变形性能的研究具有十分重要的工程意义。

目前国内外关于动车组裙板受砾石冲击的研究较少，给建立有效的砾石冲击裙板数值分析模型带来了较大困难。砾石冲击裙板问题可梳理为固体颗粒冲击平板问题。目前研究高速冲击的方法主要有试验研究和数值仿真研究。文献[14]研究了砂石平板冲击的损伤，分析了冲击物的材料、速度、外物几何特征尺寸与平板厚度之比和损伤形式、损伤程度之间的关系，提出了临界损伤速度和几何标度(Geometric)的概念，以此对外物损伤进行定量描述。本文以非线性大变形显式有限元理论为基础，采用试验和数值仿真相结合的方法，以数值仿真进行冲击规律分析。根据国内外对砂石冲击飞机发动机叶片损伤的研究[15-17]，借鉴GJB 2464A—2007《飞机透明件鸟撞试验方法》标准[18]，本文提出针对全尺寸设备舱裙板的试验方法，通过试验验证数值仿真结果从而调整相应的参数，完善数值仿真模型，并进一步通过数值仿真计算分析各因素对裙板变形性能的影响。

1 模型和方法

1.1 冲击试验模型

空气炮高速冲击试验装置由机械结构部分与数据采集部分组成，装置包括空气炮动力发射装置、弹丸脱壳装置、弹托止动减速装置、固持防护装置、速度测量装置、数据采集装置、高速摄影装置等几部分[19]。试验原理：将砾石粒子放入弹托内，然后将弹托装入空气炮管中，启动空气压缩机，当压力容器中的压力达到所需值时，打开发射活门，通过高压压差，推动弹托及粒子使其加速，在炮管前端端口有一个弹托止动减速装置与炮口固连，其中心孔直径略小于炮口直径，起到粒子与弹托分离的作用，分离后粒子依靠惯性继续飞出至完成冲击过程。

1.2 数值仿真分析

1.2.1 模型建立

1.2.1.1 有限元模型

裙板几何模型与实际冲击试验中裙板试件的几何结构保持一致，裙板的厚度尺寸范围为3～10 mm，在进行网格划分时，有限元模型选用Shell163壳单元，裙板上下各有4个螺钉孔用于裙板与设备舱支架固定，在建模时简化为加载于螺钉孔处的固支约束。划分网格后有44 750个壳单元，45 860个节点，有限元模型如图1所示。

图1 裙板有限元模型

根据高速动车组裙板设计时的特殊载荷工况的要求[20]，冲击试验中球形冲击粒子质量为0.5 kg；冲击裙板仿真工况中冲击粒子的材料与冲击试验的一致。在Hypermesh中建立不同粒径等级的球形粒子模型；图2所示有限元模型是试验工况中用到的砾石粒子，其质量为0.5 kg，直径约为73.68 mm，采用实体网格进行有限元划分后得到单元规模为15 552的球形。

图2 砾石粒子有限元模型

1.2.1.2 材料模型及参数

裙板材料为A60N1S-T5型铝合金，在有限元分析时，采用分段线性塑性材料模型(LS-DYNA对应的MAT_PIECEWISE_LINEAR_PLASTICITY本构模型)，该模型能够较好的表现金属材料在冲击载荷下的变形与破坏，采用Cowper-Symonds模型考虑应变率的影响。

按照von Mises各向同性强化模型建立材料的弹塑性应力-应变关系[21]。von Mises屈服准则可用于三维条件下判断材料是否进入塑性，即

( 1 )

裙板材料的具体参数见表1。

表1 裙板材料参数

砾石粒子使用强度等级为C30的混凝土材料模拟，在进行有限元求解时，采用MAT_JOHNSON_HOLMQUIST_CONCRETE(JHC)本构模型，JHC模型综合考虑了损伤、应变率、静水压以及压碎、压实效应，适合大应变、高应变率和高压效应情况，被广泛用于撞击、侵彻和爆炸等强动载问题的数值模拟，具体参数见表2。

表2 JHC本构模型材料参数

1.2.2 碰撞模型建立

为了真实模拟冲击试验中裙板的实际安装情况，将裙板竖直放置，通过限定其上下两端安装孔附近节点的自由度将结构固定；仿真中砾石粒子的质量和直径、冲击速度以及冲击点位置均与试验工况中相同，对砾石垂直冲击裙板中心点位置的试验工况进行数值仿真，如图3所示。

图3 砾石冲击裙板有限元模型

接触算法的选择对于模拟的真实性起着重要影响。在LS-DYNA中接触法可以分为3种类型，单面接触、点面接触、面面接触。本文模拟砾石粒子冲击裙板时的接触类型，可简化为面-面接触。其中静摩擦系数与动摩擦系数均取0.2。为了保证数值计算结果的精度，数值仿真计算时裙板的边界条件设置要与实际相符合，因此在建立有限元模型时，将裙板上的固定螺栓孔采用全约束处理，约束8个螺栓孔上节点的全部自由度。通过给冲击物中所有的节点赋予初速度来定义冲击速度，同时整个模型均受到垂直方向的重力加速度。

1.3 影响因素

粒子冲击裙板具有随机性、不确定性等特点，裙板的损伤情况与粒子冲击载荷特性有较大的关系，影响粒子冲击特性的因素主要有粒子的粒径等级、粒子的几何形状以及粒子冲击时初始时刻的接触形式。如果冲击粒子不变，影响裙板损伤程度的因素有粒子的冲击速度和冲击角度。

本文主要研究砾石粒子的粒径等级、冲击速度、冲击角度等特性对裙板抗冲击性能的影响，分析裙板在不同因素影响下的损伤规律。

2 结果

2.1 模型验证结果

为了验证数值仿真结果的可靠性，将砾石粒子以120 km/h速度冲击裙板中心位置的仿真与试验过程进行对比分析，比较裙板受冲击时的动态响应和变形过程，在对高速摄影结果和数值仿真结果进行分析时将粒子与裙板接触的初始时刻记做T=0 ms，对比分析试验和数值仿真同一时刻裙板的变形情况，如图4所示。

(a)T=0 ms (b)T=1.3 ms

T=0 ms时刻为粒子与裙板的初始接触画面如图4(a)所示；T=1.3 ms时刻粒子在与裙板接触后，速度迅速下降，裙板在球体接触点处发生局部变形，出现凹陷，如图4(b)所示；而后凹陷逐渐由冲击点中心向四周扩散，随着球体继续向前运动，裙板凹陷越变越大；T=2.6 ms时裙板瞬时凹陷深度达到最大值，如图4(c)所示；接下来粒子开始回弹，T=5 ms时粒子与裙板分离。粒子冲击裙板后，裙板受到挤压发生局部变形，撞击点处有明显的凹痕。从图4可以看出，砾石粒子冲击裙板的仿真变形过程与试验变形过程较吻合。

裙板受到冲击后，从冲击点开始，裙板结构会发生较大的变形，随后粒子继续向前运动不断挤压裙板表面，使裙板沿垂直表面方向产生较大的位移。裙板受冲击过程中，冲击点处产生的位移最大。图5为砾石粒子以120 km/h的速度垂直冲击裙板中心位置时，冲击位置处节点位移-时间响应曲线的试验和数值仿真结果对比。

图5 裙板冲击点位移时间曲线对比

由对比分析结果可知，数值仿真中裙板冲击位置处节点的位移随时间变化趋势与试验过程裙板位移的变化趋势比较相似，数值仿真和试验中裙板冲击点的最大位移比较接近。冲击过程中，裙板首先发生垂直于板面指向内侧的位移，随后在弯曲波的作用下裙板出现反弹，冲击位置处节点位移表现出振荡行为。说明本文建立的有限元模型能够较好地模拟试验过程中裙板的变形过程。

2.2 变形影响因素结果

2.2.1 砾石粒径等级因素

根据铁路线路道砟粒径级配标准，高速铁路和客运专线一般采用特级道砟。特级道砟通过方孔筛筛分为4个粒径等级22.5～31.5、31.5～40、40～50、50～63 mm。选取了4种粒径分别为25、35、45和63 mm的冲击粒子，以3种不同的速度垂直冲击裙板的结构中心位置，研究不同粒径等级的粒子垂直击打裙板时的损伤规律，共安排12个数值仿真工况。有限元分析中，冲击过程中粒子与裙板面-面接触。粒子冲击裙板后，从冲击点开始，裙板结构发生较大的变形，随后粒子继续向前运动不断挤压裙板表面，使裙板沿垂直表面方向产生较大的位移。图6为数值计算中，4种不同粒径的粒子以200 km/h的速度垂直冲击裙板中心点位置时，冲击位置处节点的位移-时间响应情况。

图6 不同粒径粒子冲击下裙板冲击点处位移时间曲线

由位移-时间曲线可以看到，对于裙板结构，在不同粒径等级的道砟以200 km/h速度垂直冲击下，最大位移可达37 mm。冲击过程中，裙板首先发生垂直于板面指向内侧的位移，随后在弯曲波的作用下裙板出现反弹，冲击位置处节点位移表现出振荡行为。不同粒径等级的粒子冲击时，裙板位移随时间的变化趋势基本相同。

将数值计算结果进行数据拟合得到裙板冲击点最大位移、凹坑深度与粒子粒径之间的函数关系。根据拟合的结果发现，裙板冲击点的最大位移与粒子粒径之间存在幂函数关系，幂次关系处于2.42～2.52之间，各工况下线性相关较好，线性相关系数R2在0.993～0.998之间，如图7所示。裙板产生塑性变形的凹坑深度与粒子粒径之间也存在幂函数关系，幂次关系处于2.25～2.54之间，各工况下线性相关较好，线性相关系数R2在0.978 0～0.988 0之间，如图8所示。

图7 裙板冲击点最大位移与粒径关系

图8 裙板凹坑深度与粒径关系

2.2.2 冲击速度因素

本文针对有砟轨道上运行的动车组展开研究，其运行速度在300 km/h以下。虽然试验和仿真过程中都把裙板固定，但实际运行过程中裙板是随着动车组高速运动的，文献[19]试验测试结果表明300 km/h运行的动车组在动车组车底区域能产生最大速度达到40 m/s左右的气流，冲击过程中砾石与裙板的运动是相互的、耦合的，所以耦合后会形成较大的相对速度。由于冲击速度超过120 km/h能产生非常明显的塑性变形，为研究随速度的变形规律，本文冲击速度范围选择在动车组运行速度内的一个区间(120～200 km/h)进行规律研究。基于这种情况，研究4种粒径的砾石粒子分别以120、160、180和200 km/h 4种不同的速度垂直冲击裙板的几何中心位置，共安排了16个数值仿真工况。图9给出了粒径为63 mm的砾石粒子以4种不同的速度垂直冲击裙板时，冲击位置处节点的位移-时间响应情况。

图9 不同速度冲击下裙板冲击点处位移时间曲线

由位移-时间曲线可以看到，对于本文研究的裙板结构，在不同速度冲击下，裙板的最大位移可达35.1 mm。随着冲击速度的增大，冲击点的位移逐渐增大，不同速度冲击时，裙板位移随时间的变化趋势基本相同。冲击过后，裙板表面会产生塑性变形出现凹坑，通过数值仿真计算得到4种速度冲击下裙板的最大位移和塑性变形情况。

将数值计算结果进行数据拟合得到裙板冲击点最大位移、凹坑深度与砾石粒子冲击速度之间的函数关系。根据拟合结果发现，裙板冲击点的最大位移与冲击速度之间存在线性关系，斜率处于0.02～0.19之间，各工况下线性相关较好，线性相关系数R2在0.994～0.999之间，如图10所示。粒径越大，最大位移随冲击速度变化的增长速率越快。裙板产生塑性变形的凹坑深度与冲击速度之间也存在线性关系，斜率处于0.014～0.1之间，各工况下线性相关较好，线性相关系数R2在0.979 0～0.998 0之间，如图11所示。

图10 裙板冲击点最大位移与冲击速度关系

图11 裙板凹坑深度与冲击速度关系

2.2.3 冲击角度因素

由于在实际工况中，砾石粒子并不一定是垂直冲击裙板表面，很有可能是以一定的角度冲击裙板的，粒子倾斜冲击裙板时，裙板的受力和变形情况较垂直入射时更为复杂，因此研究粒子以一定角度冲击裙板对倾斜打击的规律研究就显得比较重要。基于这种工况，研究砾石粒子分别以30°、60°、75°和90° 4种典型的角度冲击裙板结构中心位置，共安排了16个数值仿真工况。图12给出了砾石粒子以4种不同角度、200 km/h速度冲击裙板时，冲击位置处节点的位移-时间响应情况。

图12 不同角度冲击下裙板冲击点处位移时间曲线

由位移-时间曲线可以看到，对于本文研究的裙板结构，在不同角度冲击下，裙板的最大位移可达35.1 mm。随着冲击角度的增大，冲击点的位移逐渐增大，不同角度冲击时，裙板位移随时间的变化趋势基本相同。冲击过后，裙板表面会产生塑性变形出现凹坑，通过数值仿真计算得到4种速度冲击下裙板的最大位移和塑性变形情况。粒子以200 km/h速度、不同角度冲击裙板时，裙板均未发生破坏，只是在冲击点附近发生了明显的塑性变形，并产生了肉眼可见的冲击坑。相同粒径等级的粒子以不同速度冲击工况下，冲击角度越大，冲击点处的位移和塑性变形凹坑深度也越大。

将数值计算结果进行数据拟合得到裙板冲击点最大位移、凹坑深度与道砟冲击角度之间的函数关系。根据拟合结果发现，裙板冲击点的最大位移与冲击角度之间存在很好的二次线性关系，线性相关系数R2在0.999 0～1之间，如图13所示。当冲击速度和粒子粒径一定时，随冲击角度的增大，裙板产生的变形越大，当冲击角度增大到一定程度后，裙板的变形深度增长速度开始减缓。裙板产生塑性变形的凹坑深度与冲击角度之间也存在很好的二次线性关系，线性相关系数R2在0.995 0～1之间，如图14所示。

图13 裙板冲击点最大位移与冲击角度关系

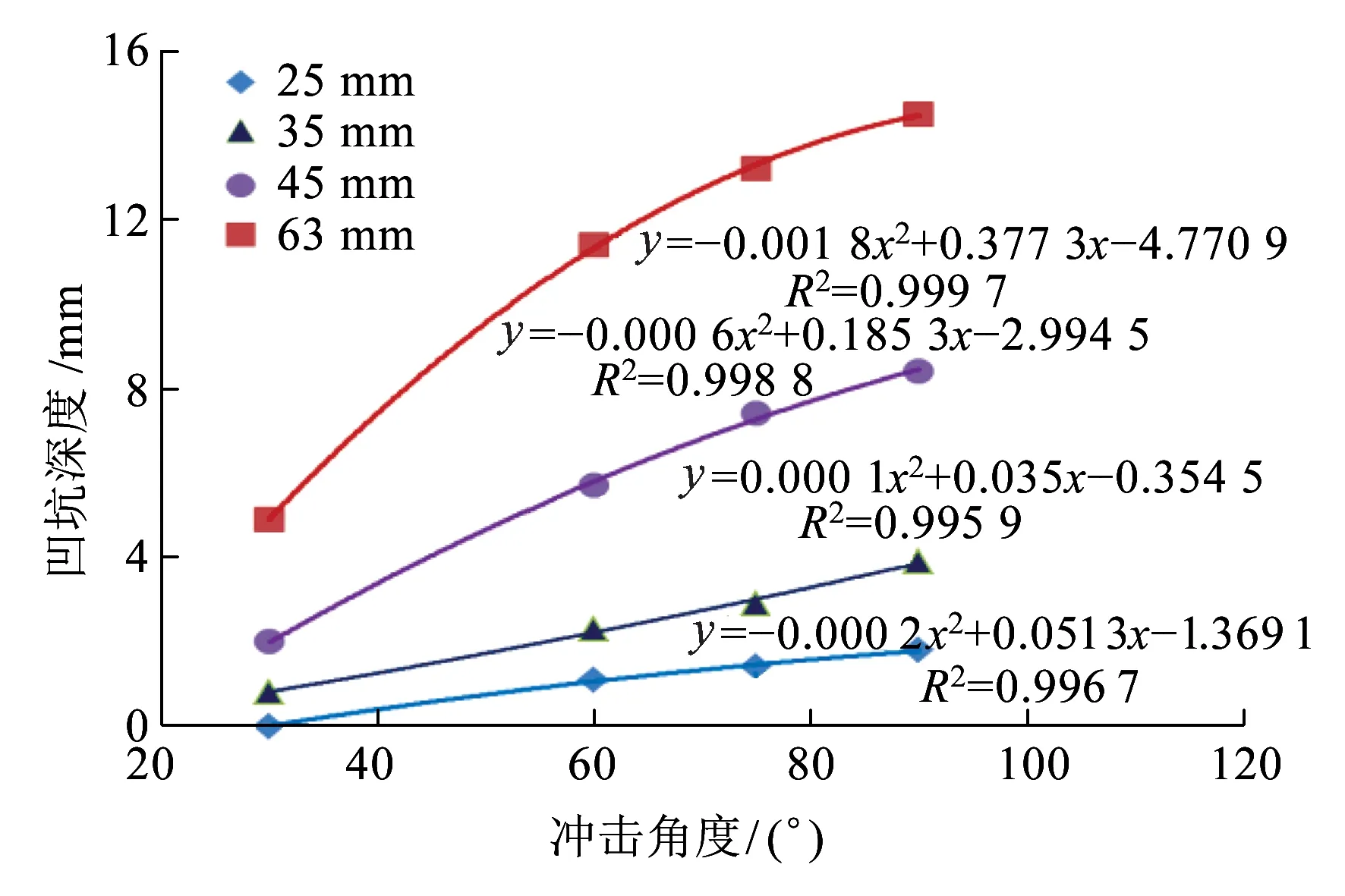
图14 裙板凹坑深度与冲击角度关系

3 讨论

本文建立砾石粒子冲击裙板的试验模型，并根据冲击试验结果建立有效的仿真模型。通过仿真模拟，分析砾石粒子粒径、冲击速度和冲击角度这三个主要的影响冲击变形因素，得到了这些因素对变形的影响规律。

4种不同粒径等级的砾石粒子以200 km/h的速度冲击裙板后，裙板表面会产生塑性变形并出现凹坑，冲击点处的变形动态响应曲线趋势一致；但随着粒径增大，整个冲击响应过程和冲击点处达到最大变形值所需的时间不断增加，冲击点处的位移和塑性变形凹坑深度也变大，位移和凹坑深度呈幂函数关系增长。在120、160和200 km/h 3个速度等级下分别拟合4种不同粒径等级砾石冲击裙板规律：随着速度增大，函数式中的幂项系数增大，幂指数变小。因为当速度一定时，冲击能量会随粒径变大成3次方关系增加，使冲击响应过程变长，变形量增速也加快。

粒径63 mm的砾石粒子以小于200 km/h的4个不同速度垂直冲击裙板时，裙板冲击点附近发生了明显的塑性变形，冲击点处的变形动态响应曲线趋势一致；随着速度增大，整个冲击响应过程和冲击点处达到最大变形值所需的时间基本相同，但冲击点处的位移和塑性变形凹坑深度会随着增大，位移和凹坑深度呈线性增长。在25、35、45和63 mm 4个粒径等级下分别拟合不同速度冲击裙板的变形规律，随着粒径增大，对应线性函数式中的一次项系数增大，即增长斜率变陡。冲击速度越高，冲击点变形深度越大，因为冲击速度提高，冲击点处的接触冲击力和冲击能量都会增大，冲击能量随速度呈2次方关系增加。其中裙板冲击点的凹坑深度随着冲击速度变化的增长速率相比最大位移的增长速率缓慢，即趋势线的斜率要小，因为在碰撞过程中产生了较大的弹性变形，冲击速度越高产生的弹性变形就越大。

砾石粒子以小于90° 4种不同角度冲击裙板，裙板冲击点最大位移和凹坑深度均与球体初始冲击角度之间呈二次函数关系增长。冲击角度越大，冲击点变形深度越大。因为在相同的冲击速度情况下，随着砾石粒子与裙板表面之间的冲击角度增大，垂直于裙板表面的分速度也就越大，垂向分速度与冲击速度呈正弦函数关系，冲击能量又与速度呈2次方函数关系，所以垂直裙板表面的主应力和接触撞击力也越大，砾石粒子与裙板接触作用的时间就更长，裙板会产生更大的弹性和塑性变形。30°冲击裙板时，球在接触到裙板之后快速弹开；而90°冲击裙板时，球在接触裙板之后没有迅速弹开，裙板需要吸收更多的能量才能使砾石粒子速度为零。相同冲击载荷下，砾石粒子冲击裙板的角度越大，冲击过程中裙板吸收的能量越大，转化成的塑性应变能也就越大，对裙板的损伤越大。裙板的凹坑深度和最大位移随着冲击角度变化的增长趋势大致相同，凹坑深度的增长速率相比瞬时最大变形深度的增长速率缓慢，即趋势线的斜率要小，因为在碰撞过程中产生了较大的弹性变形，冲击角度越大产生的弹性变形就越大。

根据本文试验对应的仿真模型，通过增加砾石的冲击速度和增加砾石的质量两个途径寻找使裙板发生撕裂破坏的临界工况。仿真结果表明：当球形砾石质量保持0.5 kg不变，速度增加到240 km/h时，裙板撕裂，如图15(a)所示；当速度保持在200 km/h不变，质量增加到0.8 kg时，裙板撕裂，如图15(b)所示。

(a)0.5 kg、240 km/h (b)0.8 kg、200 km/h图15 破坏后的裙板塑性变形图

根据图15和表3对比分析两个仿真工况：由于裙板后面有加强筋，两个撕裂孔都没有成规则的圆形；由于工况2在增加砾石质量的同时增加了冲击过程中的接触面积，所以工况2的冲击撕裂破坏临界能量稍大于工况1，工况2产生的撕裂范围也稍大于工况1。

表3 裙板撕裂临界工况

本文主要针对球形砾石仿真模型进行裙板变形规律的探究，还存在一些需要进一步研究之处：动车组实际运行工况下，砾石冲击裙板的位置是随机的，在相同的冲击载荷下，裙板不同位置由于刚度和结构的差异，冲击变形情况也有区别。由于砾石形状大小各有不同，砾石实际飞溅的速度和冲击角度也很难通过简单的分析得到，因此本文数值仿真只考虑了几个速度和角度下砾石的冲击，冲击粒子只考虑了4种不同粒径的球形砾石。此外，本文只考虑了球体与裙板表面的面-面接触，实际情况中由于砾石形状复杂多样，冲击裙板时有点接触、线接触或面接触等不同接触形式，而且在点线接触形式下等能量冲击对裙板造成撕裂的可能性更大，因此，为了了解裙板的破损性能，有必要对其他冲击接触形式做进一步研究。

4 结论

通过研究，得出以下结论：

(1)建立的有限元模型能够较好地模拟试验过程中裙板的变形过程。

(2)在球形砾石粒子冲击裙板中心位置的工况下，冲击速度相同时，粒径越大，裙板冲击点的位移和凹坑深度越大，冲击点最大位移以及凹坑深度与粒径之间存在幂函数关系，幂约为2.5。粒径相同时，冲击速度越大，裙板冲击点的位移和凹坑深度也越大，冲击点最大位移以及凹坑深度与冲击速度之间存在一次线性关系。粒径和冲击速度相同时，冲击角度越大，裙板冲击点的位移和凹坑深度也越大，冲击点最大位移以及凹坑深度与冲击角度之间存在二次线性关系。

本文分析结果为高速动车组设备舱裙板结构后续设计提供了一定的理论依据。

参考文献：

[1]中华人民共和国铁道部.高速铁路有砟轨道线路维修规则(试行)[S].北京:中国铁道出版社,2013.

[2]郭宏伟,刘树铎.京哈线秦沈段道砟飞溅防治技术的应用研究[J].铁路工程造价管理,2012,27(2):12-15.

GUO Hongwei,LIU Shuduo.Research on Application of Tract Ballast Splash Prevention Techniques[J].Railway Engineering Cost Management，2012,27(2):12-15.

[3]林建.基于计算流体力学有砟道床飞砟力学特性研究[D].北京:北京交通大学,2014.

[4]刘钢,罗强,张良,等.高速铁路有砟轨道路基设计载荷分析[J].铁道科学与工程学报,2015,12(3):475-481.

LIU Gang,LUO Qiang,ZHANG Liang,et al.Analysis of the Design Load on the High-speed Railway Ballasted Track Subgrade[J].Journal of Railway Science and Engineering,2015,12(3):475-481.

[5]KAWASHIMA K.Experimental Studies on Ballast-flying Phenomenon Caused by Dropping of Accreted Snow/Ice from High-speed Trains[J].Journal of Railway Technical Research Institute,2003,17(8):31-36.

[6]李志伟,梁习锋,张健.横通道对缓解隧道瞬变压力的研究[J].铁道科学与工程学报,2010,7(4):37-41.

LI Zhiwei,LIANG Xifeng,ZHANG Jian.Study of Alleviating Transient Pressure with Cross Passage in a Tunnel[J].Journal of Railway Science and Engineering,2010,7(4):37-41.

[7]KLOOW L,JENSTAV M.High-speed Train Operation in Winter Climate-A Study of on Winter Related Problems and Solutions Applied in Sweden[R].Norway,and Finland Transrai1,2006.

[8]BETTEZ M.Winter Technologies for High Speed Rail[D].Trondheim:Norwegian University of Science and Technology,2011.

[9]SAAT M R,BEDINIJACOBINI F,TUTUMLUER E,et al.Identification of High-speed Rail Ballast Flight Risk Factors and Risk Mitigation Strategies[C]//World Congress on Railway Research Rail Transportation and Engineering Center(RaiITEC) University of 111inois at Urbana-Champaign Department of Civil and Environmental Engineering,2013.

[10]杜欣.真实道砟颗粒的离散元建模及惯性特性优化[J].铁道学报,2014,36(2):95-102.

DU Xin.DEM Modelling and Inertia Optimization of Real Ballast Granules[J].Journal of the China Railway Society,2014,36(2):95-102.

[11]NAVARRO MEDINA F,ANDRES S,PEDRO A,et al.The Ballast Pick-up Problem.A Theoretical Approach and Two Experimental Campaigns[J].Journal of Mathematical Research and Exposition,2011,116(5):882-888.

[12]LAZARO B J.Characterization and Modelling of Flying Ballast Phenomena in High-speed Train Lines[C]//The 9th World Congress on Railway Research,2011:213-220.

[13]宿崇,杨永勤,马纪军,等.高速动车组设备舱支架结构抗疲劳性能研究[J].大连交通大学学报,2014,35(4):24-27.

SU Chong,YANG Yongqin,MA Jijun,et al.Research on Anti-Fatigue Performance of Equipment Cabin Bracket of Electric Multiple Units[J].Journal of Dalian Jiaotong University,2014,35(4):24-27.

[14]NICHOLAS T,BARBER J P,BERTKE R S.Impact Damage on Titanium Leading Edges from Small Hard Objects[J].Experimental Mechanics,1980(10):357-364.

[15]张岳青,闫蕊.飞机轮胎所造成的砂石飞溅数目的计算方法[J].航空学报,2013,34(2):309-315.

ZHANG Yueqing,YAN Rui.Calculational Method of Sandstones Rolled up by Airplane Tyres[J].Acta Aeronautica et Astronautica Sinica,2013,34(2):309-315.

[16]CHEN X,JOHN W H.Particle Impact on Metal Substrates with Application to Foreign Object Damage to Aircraft Engines[J].Journal of the Mechanics and Physics of Solids,2002,50(12):2669-2690.

[17]LIU J W,LUI T S,CHEN L S.SiO2 Particle Erosion of A356.2 Aluminum Alloy and the Related Microstructural Changes[J].Wear,1997,211(2):169-176.

[18]国防科学技术委员会.GJB 2464A—2007 飞机透明件鸟撞试验方法[S].北京:国防科学技术委员会,2007.

[19]KWON H B,PARK C S.An Experimental Study on the Relationship between Ballast Flying Phenomenon and Strong Wind under High Speed Train[C]//Montreal: Proceedings of the World Congresson Rail Research,2006.

[20]杜秋男,李瑞淳.高速动车组裙板设计研究[J].铁道车辆,2008,46(6):16-17.

DU Qiunan,LI Ruichun.Design and Research on Apron Boards for High Speed Multiple Units[J].Rolling Stock,2008,46(6):16-17.

[21]QUINN A D,BAKER C J,WRIGHT N G.Wind and Vehicle Induced Forces on Flat Plates-Part 2:Vehicle Induced Force[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89(9):831-847.