考虑再生制动能利用的城市轨道交通列车节能运行优化方法研究

冯 瑜，陈绍宽，冉昕晨，柏 赟，贾文峥

(1.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京 100044；2.交通运输部科学研究院 城市交通研究中心，北京 100029；3.郑州市轨道交通有限公司，河南 郑州 450000)

城市轨道交通因其安全、舒适、运量高、节能等特性已成为各大城市重点发展的公共交通方式，但其线网规模扩大导致城市轨道交通系统能耗在交通运输业总能耗中所占比重不断提高[1]。通过全类别电能消耗统计可知，列车牵引用电量占比达到50%。因此，牵引能耗的减少将对整个系统节能具有重要影响。降低列车牵引能耗的方法主要包括两个方面：降低运营过程中牵引供电系统和车轨系统的能量消耗，例如优化牵引系统、降低轮轨摩擦损耗等；提高列车制动能量的管理和利用水平，包括运行过程优化及运行图协调、储能系统建设和可逆变电站应用等[2]。其中，列车运行过程优化及运行图协调是对既有设施影响小、投资成本低的节能措施。

针对轨道交通列车运行过程的节能优化问题，国内外学者开展了大量研究工作，主要是围绕目标函数构建、控制变量选取以及求解算法设计三个内容。模型多采用单目标和多目标两类目标函数，最初将能耗最小作为目标，而多目标优化模型则由日本学者Shoji最早提出[3]。控制变量方面主要考虑列车速度控制和惰行工况控制两类，前者以速度曲线为对象研究节能策略[4]，后者主要以惰行点位置信息为目标确定节能控制策略[5-6]。求解算法通常采用解析法、数值法和智能算法等，前两种方法在早期研究中较为常用[7-9]，随着研究问题的逐渐复杂，目前多采用智能算法求解，包括模糊控制[10]、人工神经网络、遗传算法[5-6]、蚁群算法[11-12]、离子群算法等[13]。

运行图协调工作通常围绕多列车运行优化问题展开，主要方法包括：降低峰值供电需求，例如调整列车到发与停站时间以降低瞬时最大牵引功率[14]；提高再生制动能的利用率，例如增加列车间再生制动能可利用时间[15-16]、优化追踪列车操纵序列提高再生制动能吸收利用率[17]等。从研究结果看，运行图协调可实现7%～14%的节能效果[2]。

在已有研究中，多分别针对单列车节能运行与多列车运行调整开展研究，较少考虑综合发挥两者协同优化的效果，易造成前者再生制动能利用率偏低、后者总牵引能耗偏高的局面。为克服上述问题，本文在“四阶段”速度控制的单列车站间运行节能优化基础上，构建考虑多列车再生制动能利用的时刻表优化模型，通过案例研究分析两者协同优化策略的节能效果。

1 单列车站间节能运行优化

根据庞特里亚金最大值定理，可获得以能耗为目标的“四阶段”最优控制策略，即最大加速度牵引—巡航—惰行—最大减速度制动。列车在定时站间运行策略下，对应不同的速度距离曲线，如图1中的曲线1、曲线2。速度曲线不同导致列车运行过程中的能耗差异，如何确定能耗最小的速度曲线是单列车站间节能运行优化的关键。

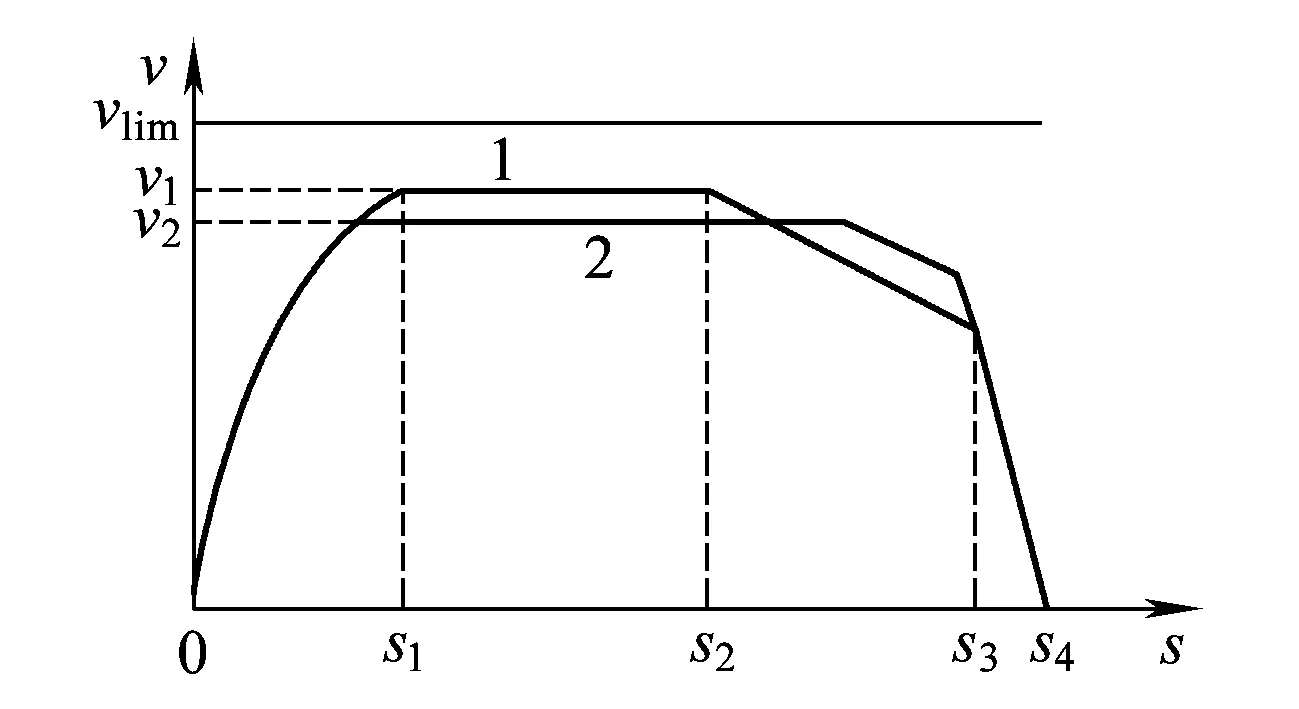
图1 列车站间运行过程

基于牵引力做功的能耗计算方法，分析各个阶段能耗产生过程如下。

(1)牵引阶段：通过列车牵引特性曲线确定给定速度v的牵引力F1(v，s)，计算列车牵引能耗为E1=∑F1(v，s)·Δs1/3 600，Δs1为牵引阶段一个时间步长(通常取1 s)内的距离。

(2)巡航阶段：此过程列车速度保持不变，需根据阻力大小确定牵引力或制动力工况。牵引工况时牵引力为F2(v，s)，牵引能耗为E2=∑F2(v，s)·Δs2/3 600，Δs2为巡航阶段一个时间步长内的距离；制动工况时，牵引能耗为0。

(3)惰行和制动阶段：列车处于惰行或制动工况，牵引能耗为0。

在定时策略下，列车基于“四阶段”控制策略运行时其巡航过程是否存在通常由站间距大小决定。当站间距较大时，为满足站间运行时分和限速约束，列车巡航运行保持较高速度；当站间距较小时，巡航运行过程较短或不存在，站间运行过程包括牵引、惰行和制动三个阶段。

按照“四阶段”控制策略运行的列车速度曲线的确定仅与牵引阶段末速度有关，模型自变量可简化定义为牵引阶段的末速度，因此可得任一区间内单列车定时节能优化运行的模型为

( 1 )

2 基于再生制动能利用的多列车运行时刻表优化模型

2.1 问题的描述及假设条件

同一供电分区内两列车同时分别处于制动和牵引工况时，牵引工况列车需要电能而制动工况列车恰好产生反馈电能，此时制动列车可将反馈电能传递给牵引列车使用。再生制动能利用量与两列车所处工况的重叠时间长短紧密相关。列车追踪运行间隔较短时制动列车和牵引列车发生重叠的概率较大，适于开展多列车再生制动能利用优化研究。此外，列车制动过程中只有电制动阶段产生的再生制动能量可回馈至电网再利用，而当速度降低到某一给定值(例如8 km/h)后列车只采用空气制动，因此在计算制动阶段时间区域时须排除低于给定速度的空气制动阶段。

本文研究主要假设条件：

(1)再生制动能量可及时反馈供其他列车使用。

(2)不考虑传输过程中的时间延误和网压变化对能源利用的影响。

(3)不同列车在同一站间区间的操纵策略相同。

(4)不同列车在同一车站的停站时间相同。

(5)再生能随时间均匀产生，且再生制动能从产生到被利用的过程中的传输效率为常量。

2.2 再生制动能利用场景分析

按两列车先后位置不同，可将再生制动能利用情景分为“Ⅰ：前车制动-后车牵引”与“Ⅱ：前车牵引-后车制动”两种，如图2、图3所示。相关符号定义见表1。

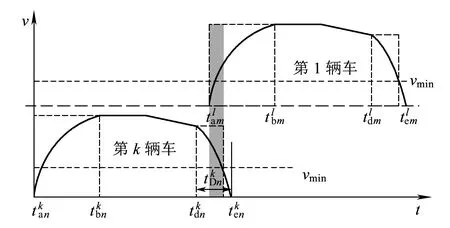
(a)情形1

(b)情形2图2 场景Ⅰ重叠时间

(a)情形1

(b)情形2图3 场景Ⅱ重叠时间

符号含义符号含义i第i个区间j第j列车tjai第j列车在第i个区间牵引阶段开始时刻,stjdi第j列车在第i个区间制动阶段开始时刻,stjbi第j列车在第i个区间牵引阶段结束时刻,stjei第j列车在第i个区间制动阶段结束时刻,stjAi第j列车在第i个区间牵引阶段持续时间,stjDi第j列车在第i个区间制动阶段持续时间,sN1区间数N2列车数m,n站间区间编号,m≤nRi列车在第i区间的运行时间,s

对于场景Ⅰ又可分为以下两种有效情形，其他情形列车再生制动无可利用的重叠时间。

情形1：列车k处于制动阶段后，列车l才开始牵引，重叠时间如图2中阴影区域所示。

情形2：列车l处于牵引阶段后，列车k才开始制动，重叠时间如图2中阴影区域所示。

同理，可得场景Ⅱ中重叠时间不为0的两个有效情形分别为“前车处于牵引阶段后，后车才开始制动”和“后车处于制动阶段后，前车才开始牵引”，如图3中的情形1和情形2。

2.3 模型构建

2.3.1 参数设置

为方便描述，表2给出模型构建中所需其他参数变量的符号及含义。

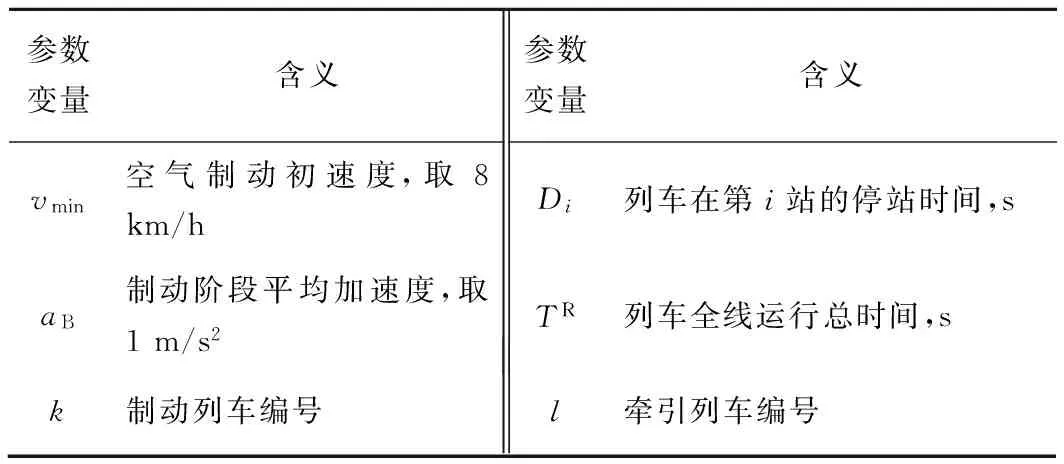
表2 参数变量的设置

2.3.2 目标函数分析

本文构建时刻表优化模型的自变量为牵引阶段持续时间、发车间隔与停站时间，目标函数为可利用的再生制动能最大。根据列车l牵引阶段与列车k制动阶段开始时间的先后顺序，场景Ⅰ有效重叠时间表达式为

( 2 )

与场景Ⅰ类似，场景Ⅱ中有效重叠时间的表达式为

( 3 )

T0|t=1=

( 4 )

T0|t=2=

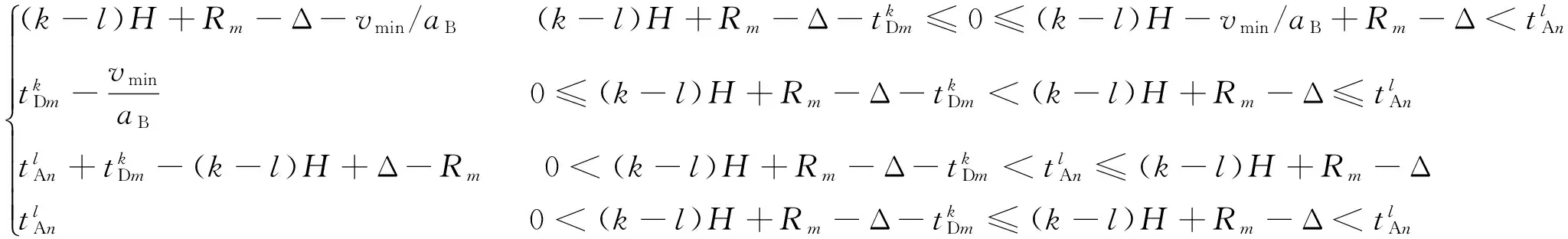
( 5 )

( 6 )

式中：λt为判断各场景中的目标列车是否处于同一牵引供电分区的0-1变量，若是则取值为1，否则为0。

优化模型的目标函数为

( 7 )

式中：Eu为可利用的再生制动能；Er为再生制动的产生量(机械能)；EBij为站间区间i内第j列车在再生制动阶段内动能的变化量；TBij为站间区间i内第j列车在再生制动阶段内的运行时间；η为再生制动能的传输效率，可取0.8[8]。

2.3.3 约束条件

列车运行时刻表需满足一定的约束条件，具体包括：

(1)发车间隔约束：需满足最小发车间隔约束H(l)，而最大发车间隔根据实际客运量、运用列车数量等确定，记做uh。

(2)停站时分约束：给定时刻表停站时间，可根据实际客流量确定。实际运营中停站时间具有一定波动性，其上、下限分别记作ld、ud。

(3)全线运行总时间约束：通常根据线路长度、列车运行速度、折返时间等计算，为应对突发情况或列车晚点，设有运行恢复时间，全线运行总时分上、下限分别记作lR、uR。

综上所述，建立优化模型为

( 8 )

2.4 求解算法

本文所建模型属非线性优化问题，数值方法求解时迭代过程耗时长且易陷入局部最优，遗传算法具有收敛性好、鲁棒性高、步骤简单等优点。本文采用遗传算法求解，对变量编码、初始种群、适应度函数、遗传操作(选择、交叉、变异)等分别进行设计。

步骤1编码并生成初始种群：发车间隔H、停站时间Di和牵引持续时间tAi是决策变量，将其按各区间顺序依次用二进制编码形成染色体(H1，D1，tA1，…，HN1，DN1，TAN1)，如图4所示。随机生成初始种群数N=80，满足式( 8 )约束。

图4 编码

步骤3选择操作：计算每个个体被选中遗传到下一代的概率pi=fi/∑fi，i=1，2，…，N，采用轮盘赌方法确定遗传到下一代的个体。

步骤4交叉操作：随机选择两个上一代染色体Ci，Cj，用双点交叉方法以pc=0.50的交叉概率产生新染色体X，Y，并进行可行性检验。若X，Y满足式( 8 )，则取代上一代染色体，否则保持上一代染色体不变。

步骤5变异操作：随机选择染色体变异点位，以pm=0.01的概率将变异点做“0-1”翻转，形成新个体，并进行可行性检验，若通过则替代上一代染色体，否则保持上一代染色体不变。

步骤6重复步骤2～步骤5，直到满足最大迭代次数G=500，返回最优染色体编码并解码，获得发车间隔、停站时间和牵引时间序列反映列车运行具体过程，其适应度值即为可利用的再生能数值。

3 案例分析

本文选用北京某地铁线路为案例，在线路平纵断面数据及运营资料基础上，研究所建模型的实用性和有效性。列车采用6B编组(3M3T)，满载(AW2)时总重为282.08 t，最大速度为80 km/h，在750 V网压下列车的最大牵引力为23 kN/电机，最大制动力为19 kN/电机。基本运营数据和线路情况见表3。

表3 基本运营数据和线路情况汇总

3.1 单列车站间区间节能分析

本章应用第2章中建立的单列车站间节能优化方法，分析案例线路中列车在12个不同区间的列车速度曲线和能耗数值，具体结果见表4。

表4 单列车站间节能运行结果数据

由表4可知，单列车站间节能运行策略下，可通过提高牵引结束末速度、增加惰行所占比例有效减少牵引能耗。案例线路中站间距大于1 500 m的区间，如区间2、5、6和8节能效果明显；在站间距小于1 100 m的区间，如区间9、12节能空间不足，“四阶段”退化为“三阶段”策略。因此，单列车站间“四阶段”节能运行策略在大站间距区间节能空间较大。案例线路中10个区间站间距均大于1 100 m，通过优化最多可节省25%的牵引能耗，全线平均节能率为13.94%。

3.2 再生制动能利用优化分析

为验证多列车时刻表优化节能效果，本节以3列车为对象，暂不考虑单列车站间运行优化节能，研究从第1列车在第一站出发到第3列车在最后一站停车过程中前后两列车之间对再生制动能的利用情况。决策变量取值范围结合运营数据根据2.3节所述方法确定：牵引阶段持续时间为10～37 s；发车间隔为116～230 s；停站时间为30～60 s。

对优化模型进行求解，结果见表5，优化后的时刻表与初始时刻表的重叠时间对比见表6。

表5 优化结果

表6 优化前后时刻表对比

从表6可知列车再生制动能可利用重叠时间由124 s增至187 s，可利用量从162.54 kW·h提高至235.66 kW·h，增幅约为45%。比较优化后的自变量取值与初始值，发车间隔时间和停站时间变化幅度较小，平均牵引阶段持续时间从21 s增加到26 s。结果表明多列车时刻表优化模型在运营时间指标较小波动范围内可明显提高可利用再生制动能量。

3.3 单列车节能运行与多列车再生制动能利用的协同优化分析

仅考虑多列车时刻表节能优化，通常会增加牵引阶段持续时间，导致单列车牵引能耗的增加；而单列车站间节能优化方法可明显降低牵引能耗，因此有必要开展单列车站间节能运行与多列车运行的协同优化研究。

协同优化过程中，单列车节能优化模型的自变量为牵引阶段的末速度(牵引阶段的持续时间)，而牵引阶段持续时间恰是多车模型的自变量之一。因此可先求解单列车优化模型，获得最优节能运行策略下牵引阶段持续时间，再输入多列车模型，根据前后列车的位置和运行状态计算重叠时间和再生能耗，实现两个模型的协同优化。

图5为求解多列车模型遗传算法中适应度的迭代变化过程，优化结果见表7。图5表明算法是收敛的，在150代之前，适应度值随进化代数变化显著，在400代之后最优个体的平均适应度值趋于稳定。

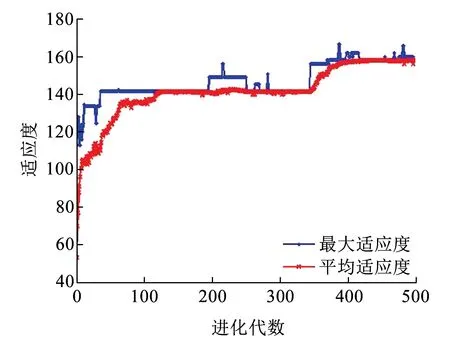
图5 适应度值的迭代情况

发车间隔H/s停站时间D/s重叠时间T/s可利用的再生制动能/(kW·h)196(45,30,35,43,42,47,41,50,56,38,35,42)166214.61

与初始时刻表相比，优化后发车间隔从210 s减少至196 s，可利用的再生制动能从162.54 kW·h增加至214.61 kW·h，增幅为32.1%。与仅优化时刻表相比，可利用再生制动能的增加幅度低12.9%。

为进一步反映城轨列车群的运行协同优化效果，本文设计20列车的研究情景，分别按照未优化(方案O)、单列车站间节能优化(方案A)、多列车时刻表优化(方案B)以及二者协同优化(方案C)4个方案计算列车的全线运行总能耗。总能耗数值等于列车牵引能耗减去可利用的再生制动能，具体结果见表8，其中可利用的再生制动能由式( 7 )计算得到。

表8 三种方案优化的结果数据

从表8可知，与初始方案O相比，方案A、B、C的节能效果分别为8.06%、16.04%、24.07%，方案C的节能效果最优。3个列车节能运行优化方案中，方案A站间运行能耗最低，可利用的再生制动能也最少，全线总能耗最大；方案B站间运行能耗最高，可利用再生制动能最大，全线总能耗次之；方案C站间运行能耗最低，可利用再生制动能较低，全线总能耗最小。结果表明，结合单列车站间节能运行与多列车时刻表优化两个节能策略，可实现牵引能耗与可再生制动能利用的最优组合。

4 结束语

本文结合建立的单列车站间运行节能优化模型和基于再生制动能利用的多列车时刻表优化模型，应用北京地铁某线路的数据开展城市轨道交通运行节能优化方法有效性研究。不同场景案例研究结果表明：单列车站间节能运行优化最大幅度降低列车牵引能耗，但可利用再生制动能最少，全线总能耗最大；多列车时刻表节能优化可保证可利用再生制动能最多，但单列车牵引能耗最大，全线总能耗较大；结合二者可获得最小的站间运行牵引能耗，较多的可利用再生制动能，全线总能耗最小。因此，在城市轨道交通列车运行能耗管理工作中，结合牵引能耗和可利用再生制动能的协同优化是最为有效的节能策略之一。需要注意的是，本文采用的牵引力和制动力均为最大值，固然对降低单列车牵引能耗有益，但同时意味着两列车的牵引工况和制动工况持续时间均最短，其重叠可能性及时间均较小，影响到多列车间再生制动能的利用效率，因此研究牵引和制动工况持续时间对总能耗的影响是下一步工作的重点。

参考文献：

[1]荀径,杨欣,宁滨,等.列车节能操纵优化求解方法综述[J].铁道学报,2014,36(4):14-20.

XUN Jing,YANG Xin,NING Bin,et al.Survey on Trajectory Optimization for Train Operation[J].Journal of the China Railway Society,2014,36(4):14-20.

[2]GONZALEZ-GIL A,PALACIN R,BATTY P.Sustainable urban Rail Systems:Strategies and Technologies for Optimal Management of Regenerative Braking Energy[J].Energy Conversion & Management,2013,75(5):374-388.

[3]MIYAMOTO S,YASUNOBU S,IHARA H.Predictive Fuzzy Control and Its Application to Automatic Train Operation System[J].Anal of Fuzzy Inf,1987:59-72.

[4]丁勇,毛保华,刘海东,等.定时约束条件下列车节能操纵的仿真算法研究[J].系统仿真学报,2004,16(10):2241-2244.

DING Yong,MAO Baohua,LIU Haidong,et al.An Algorithm for Energy-efficient Train Operation Simulation with Fixed Running Time[J].Journal of System Simulation,2004,16(10):2241-2244.

[5]CHANG C S,SIM S S.Optimising Train Movements Through Coast Control using Genetic Algorithms[J].IEE Proceedings-Electric Power Applications,1997,144(1):65-73.

[6]WONG K K,HO T K.Coast Control for Mass Rapid Transit Railways with Searching Methods[J].IEE Proceedings-Electric Power Applications,2004,151(3):365-376.

[7]HOWLETT P G.An Optimal Strategy for the Control of a Train[J].Journal of the Australian Mathematical Society,1990,31(4):454-471.

[8]HOWLETT P G,PUDNEY P J,XUAN V.Local Energy Minimization in Optimal Train Control[J].Automatica,2009,45(11):2692-2698.

[9]KHMELNITSKY E.On an Optimal Control Problem of Train Operation[J].IEEE Transactions on Automatic Control,2000,45(7):1257-1266.

[10]BAI Y,HO T K,MAO B H,et al.Energy-efficient Locomotive Operation for Chinese Mainline Railways by Fuzzy Predictive Control[J].IEEE Transactions on Intelligent Transportation Systems,2014,15(3):938-948.

[11]KE B R,CHEN M C,LIN C L.Block-layout Design Using MAX-MIN Ant System for Saving Energy on Mass Rapid Transit Systems[J].IEEE Transactions on Intelligent Transportation Systems,2009,10(2):226-235.

[12]KE B R,LIN C L,YANG C C.Optimisation of Train Energy-efficient Operation for Mass Rapid Transit Systems[J].IET Intelligent Transport Systems,2012,6(1):58-66.

[13]贺德强,周继续,李宇轩,等.基于矩阵离散法的地铁列车节能优化操纵方法及实现[J].铁道学报,2015,37(7):9-14.

HE Deqiang,ZHOU Jixu,LI Yuxuan,et al.Energy Saving Optimization Operation Method for Metro Train Based on Matrix Discrete Method on Its Implementation[J].Journal of the China Railway Society,2015,37(7):9-14.

[14]KIM K M,OH S M,HAN M.A Mathematical Approach for Reducing the Maximum Traction Energy:The Case of Korean MRT Trains[C]//In Proceedings of the International Multi Conference of Engineers and Computer Scientists,2010:2169-2173.

[15]SU S,LI X,TANG T,et al.A Subway Train Timetable Optimization Approach Based on Energy-efficient Operation Strategy[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(2):883-893.

[16]LI X,HONG K L.An Energy-efficient Scheduling and Speed Control Approach for Metro Rail Operations[J].Transportation Research Part B Methodological,2014,64(4):73-89.

[17]唐海川,王青元,冯晓云.地铁列车追踪运行的节能控制与分析[J].铁道学报,2015,37(1):37-43.

TANG Haichuan,WANG Qingyuan,FENG Xiaoyun.Energy Saving Control of Metro Train Tracking Operation[J].Journal of the China Railway Society,2015,37(1):37-43.