基于新型过渡控制策略的分段直接转矩控制

向超群，陈春阳，成 庶

(中南大学 交通运输工程学院，湖南 长沙 410075)

城轨站间距较小，启制动过渡频繁，停车精度要求高，要求车辆在全速范围内能平稳调速而且转矩脉动小。城轨牵引系统是列车安全、稳定运行的关键，与一般交流调速系统相比，具有牵引功率大、开关频率低的特点[1]。现有的牵引变流器控制方法大多采用矢量控制，但是存在抗扰动能力差、转子磁链很难准确测量、矢量变换过程繁琐等缺点[2-3]。1985年德国鲁尔大学DEPENBROCK教授提出直接转矩控制[4]，其优势在于构造简单、转矩响应迅速和参数鲁棒性好等。文献[5]通过大量试验验证了在轨道交通牵引领域，直接转矩控制可以获得更好的动态响应以及较少的依赖电机参数。由于直接转矩控制采用Bang-bang控制，不可避免的存在转矩脉动[6]。利用改进型的直接转矩控制，能较好地改善变流器的低速性能和转矩脉动[7-9]。文献[7]引入了SVPWM对改进型的直接转矩控制进行改良，使之能适用于全速范围，但是不适用大功率变流低开关频率的要求。文献[10]在六边形磁链控制的基础上，引入了十八边形折角控制，减弱了逆变器反射至中间直流环节的5、7次谐波。但是在额定频率点以后，定子上的基波电压会减小，影响牵引功率的发挥。文献[1]在低速段使用圆形磁链控制，在高速段使用六边形磁链控制，在大功率应用中取得了较好的静、动态性能。文献[11]在低速段引入了改进型的磁链观测器，减小了低速时磁链观测带来的误差，在高速段根据转矩角变化选择电压矢量，减小转矩脉动，实现了牵引电机全速范围内的运行。文献[12]在低速段采用圆形磁链控制，在中速区域采用十八边形磁链控制，在高速区采用六边形磁链控制，建立了异步牵引电机在全速域范围内运行的直接转矩控制方案。文献[13]在全速范围内，将定子磁链轨迹扩展为圆形-三十边形-十八边形-六边形，改善了定子电流的正弦度，消除了特定次谐波。但要实现多种磁链轨迹与控制，算法与设计的实现都比较复杂。文献[1、11-13]中均未详细分析两种控制方式过渡的动态过程。文献[14]提出了一种适合于全速范围的直接转矩控制系统仿真模型，在圆形磁链轨迹向六边形磁链轨迹过渡时，仅以速度作为过渡依据，未分析过渡时磁链突变引起的不平滑现象。文献[15-16]均提出了速度容差和磁链容差同时判断的过渡条件，当两个条件同时满足，但过渡时刻如果输出减小转矩的电压矢量，则存在无法过渡的问题。本文基于此思路，进行了分段直接转矩控制过渡过程的研究。

1 牵引异步电动机分段改进的直接转矩控制

在一个周期内，相比于六边形控制，圆形磁链轨迹直接转矩控制输出的电压矢量数量更多，定子磁链更加逼近圆形，减少了定子电流谐波成分[17-19]。但是由于开关频率高，在大功率牵引领域的应用会受到一定限制。

六边形磁链轨迹直接转矩控制，磁链轨迹由6个电压矢量组成，在一个周期内只输出6个不同的电压矢量，与圆形磁链轨迹控制相比，减少了开关次数且降低了开关损耗。在高速运行时，磁链估算模型误差减小，其定子磁链模型也能较好地符合控制要求，但在低速状态下存在磁链模型估计不准确、脉动转矩大的问题[20-21]。

针对城轨车辆运行需求和城轨牵引变流器的特点，依据不同的速度范围选择相应的控制方式，从而满足全速范围内的高品质直接转矩控制[7]。在额定转速30%以下时，选择圆形磁链控制，从而获得较为平滑的转矩变化，提高城轨车辆运行的舒适性，降低车辆启动对车钩等连接部件的冲击。高速时，采用六边形磁链控制，可适当降低开关频率，减少开关损耗，提高运行可靠性[17]。改进型直接转矩控制原理如图1所示。

图1 分段改进直接转矩控制系统原理

由图1可知，分段改进直接转矩控制系统主要包括：转矩计算、磁链观测、圆形/六边形磁链轨迹控制方式以及过渡判断模块。

圆形磁链轨迹直接转矩控制和六边形磁链轨迹直接转矩控制是直接转矩的两种不同实现方法，由于在电压矢量的选择上存在差异，因此形成了两种不同的磁链轨迹。本文的控制方法需要在同一模型中使用两种不同的方法，如果仅用单一的转速作为过渡判据，可能会造成两种控制方式的冲突，导致一方电压矢量选择错误，引起转速和转矩的波动，进而导致城轨车辆运行品质的下降，同时还使机械部件受到较大的冲击。本文对过渡状态进行了详细分析，并针对可能出现的情况提出一种新的过渡控制策略。

2 一种新型分段直接转矩控制过渡控制策略

2.1 高速段电压空间矢量控制方法

将定子旋转磁链空间矢量在βa、βb、βc三相轴系上的磁链分量分别定义为ψβa、ψβb、ψβc。

定义磁链开关变量为

( 1 )

式中：下标n分别取a、b、c。

定义每相桥臂的电压开关状态变量为

( 2 )

式中：n=a、b、c。

根据式( 3 )可以将磁链开关信号转换为取反后的电压开关信号。

( 3 )

U4(011)—U5(001)—U6(101)—U1(100)—U2(110)—U3(010)顺序输出电压矢量，磁链将沿六边形轨迹逆时针旋转。

2.2 低速段电压空间矢量控制方法

圆形磁链调节也采用Bang-bang控制。滞环比较器的输入为

( 4 )

将给定磁链与实测磁链差值Δψs输入与滞环比较器环宽±εψ进行比较，当输入不在滞环范围之内时，表示给定与输出相差较大，应根据比较器的输出φ改变电压矢量，将输入绝对值减小。

( 5 )

式中：εψ为滞环比较器滞环宽度。

当φ=0时，应增大磁链，当φ=1时，应减小磁链。磁链滞环将实际值控制在以给定值为基准，以±εψ为容差的范围内波动。

电压空间矢量与定子磁链夹角不同，在相应坐标轴上的投影也不同，为了更好地区分不同电压矢量的影响，可以将电压矢量空间均分为6个扇区，电压矢量U1将扇区S1均分为2等分，具体扇区划分如图2所示。

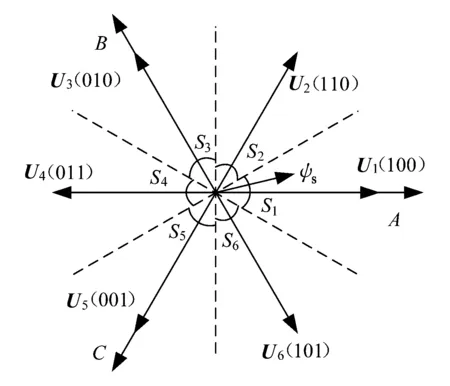
图2 圆形磁链控制方式扇区分布

转矩计算公式为

( 6 )

式中：Te为电磁转矩；Pn为极对数；Lσ为漏感；ψs为定子磁链；ψr为转子磁链；φ为磁通角。从式( 6 )可知，保持定转子磁链幅值不变，改变磁通角即可改变转矩。磁通角可以通过施加不同的电压矢量调整。

( 7 )

式中：εT为滞环比较器容差。

根据电压空间矢量对定子磁链幅值和磁通角(即转矩)的影响建立开关表，见表1。

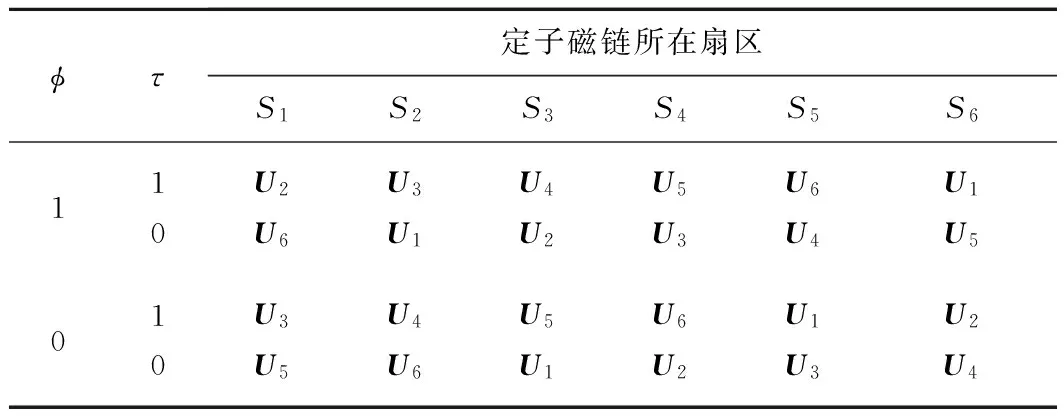
表1 逆变器的开关表

2.3 过渡点速度判据分析

分段直接转矩控制，两种控制方式的切换以电机转速为前提条件。当速度达到某一临界值(30%额定转速)，大于临界点时，控制方式从圆形控制方式过渡到六边形控制方式，当扰动出现，速度减小到临界点以下，六边形控制方式将过渡回到圆形控制方式。当扰动较为频繁时，可能引起系统震荡，导致控制失败。因此设置滞环控制器，避免控制方式的频繁切换。

过渡速度应该满足以下关系

|v-vswitch|≥|εv|

( 8 )

式中：v为实际转速；vswitch为临界过渡速度；|εv|为速度滞环宽度。

2.4 过渡点磁链判据分析

前文中提到两种控制方式的不同，导致磁链轨迹不同，如果在临界速度条件满足后立即过渡，可能会造成磁链突变，带来电流尖峰，造成转矩脉动。为了分析方便，将六边形磁链和圆形磁链绘制在同一坐标系中，如图3所示。

图3 六边形磁链轨迹与圆形磁链轨迹

速度小于等于30%额定转速时，电机运行于圆形磁链，假设在s点时(位于S6扇区)，达到过渡临界速度，由圆形磁链逆变器开关表1可知，此时输出的电压矢量有4种可能，分别为U1、U2、U4、U5。

2.4.1 无法过渡的原因分析

假设在U4时，进行控制方式的过渡，此时的定子磁链空间矢量满足

( 9 )

根据六边形电压矢量选择规则，磁链分量均位于滞环内，无论转矩发生何种变化，输出的电压矢量保持不变。在电压矢量U4的作用下，转矩持续减小，导致速度下降，当速度下降至速度判据下限时，控制方式将由六边形磁链控制过渡回圆形磁链控制。假设磁链轨迹继续沿U4方向运行，当磁链轨迹与H3边界相交时，定子磁链空间矢量满足

因此根据式( 1 )、式( 3 )可得

综合之前的输出电压失量为U4(011)，可判断下一输出为U7(111)，系统持续输出零矢量，将无法继续正常进行过渡。

图4 无法顺利过渡磁链轨迹

如图4中黑框标注位置，在S6扇区时，满足速度过渡临界值，输出电压矢量U4。由于U4持续减小转矩，将导致电机转速下降，在一段时间后，速度下降至过渡临界值，控制方式转换为圆形磁链轨迹控制。系统根据圆形规则输出电压矢量U1，增大磁链和转矩，速度再次上升。如此反复，直到运行至S2扇区时，输出正确的电压矢量，控制方式才得以顺利过渡。

同理可分析得出在U5时过渡，系统也将持续输出零矢量，导致无法继续正常运行。

2.4.2 无法平滑过渡的原因分析

假设在U2时，进行控制方式的过渡，此时的定子磁链空间矢量满足式( 8 )。磁链轨迹沿U2继续运行，当磁链轨迹与H6边界相交时，此时的定子磁链空间矢量满足

因此根据式( 1 )、式( 3 )可得

综合之前的输出电压失量为U2(110)，可判断下一输出为U3(010)，系统顺利过渡。

如图5中箭头所指位置，在S6扇区时，满足速度过渡临界值，输出电压矢量U2。由于U2作用增大转矩，电机转速继续上升，磁链轨迹沿U2继续运行，直到与H6边界相交，改变电压矢量，磁链轨迹转入六边形磁链控制方式，与前述分析一致。

图5 无法平滑过渡磁链轨迹

同理可分析得出在U1时系统也能过渡，但是磁链轨迹发生了畸变。

2.5 平滑过渡控制策略

从以上分析可知，当圆形磁链轨迹控制方式向六边形磁链轨迹控制过渡后，由于过渡时机选择不正确，输出电压矢量使转矩减小，导致转速下降，磁链向反方向运行，如果不能及时纠正则会带来磁链畸变和电流尖峰的不利影响。而速度滞环的宽度|εv|决定了六边形磁链轨迹控制切换回圆形磁链轨迹控制的时间tswitch，两者关系为

|εv|∝tswitch

(14)

此种情况下为了减小电流冲击，应保证速度滞环宽度尽量小，但是不可避免地增加了控制方式的切换频率，两者有着不可调和的矛盾。

采用新型过渡控制策略后，由于过渡时不选择使转矩减小转速下降的电压矢量，因此可避免转速持续下降的状况，速度滞环宽度仅避免车辆正常行驶时的速度波动即可，一般可选择±1km/h。

综合2.3与2.4节的分析可知，只用速度临界点过渡，可能导致磁链轨迹不能迅速建立，甚至无法过渡。以速度判据作为过渡的前提，还应综合考虑磁链位置和电压矢量。

图6 过渡扇区示意

从图6可知，当六边形磁链与圆形磁链相切时，两者磁链幅值相等，此时过渡，磁链轨迹改变最小。由此可建立以下磁链过渡条件

同时，相角还应满足

k=0，1，2，…

(16)

为了避免反复过渡，引入滞环比较器。过渡时磁链应满足

||ψ|-|ψswitch||≤|εψ|

(17)

|θ-θswitch|≤|εθ|

(18)

过渡时电压矢量的判断与磁链所处位置相关，当磁链幅值满足切换条件时，磁链处于两扇区分界线附近。为避免扇区误判，将扇区重新划分为T1～T6，可用式(19)表示。

为满足平滑过渡要求，速度与磁链满足过渡要求，电压矢量Us还应满足以下条件：电压矢量应增大转矩，要求sinγ>0，γ为电压矢量Us与磁链ψs的夹角；为满足六边形磁链轨迹控制要求，过渡电压矢量作用方向应与六边形磁链轨迹运动方向一致。

如图6所示，当过渡点位于T2扇区时，综合过渡点电压矢量分析可知，当电压矢量输出为U4时，磁链突变最小，且能顺利过渡。因此为了平滑过渡，尽量减小磁链波动，过渡时，输出电压矢量还应满足表2。

表2 过渡点电压矢量选择

以电机转速为前提，综合考虑过渡时的磁链幅值、相角以及此时作用的电压矢量。当所有过渡条件均同时满足，可以进行控制方式的切换。此时可以满足平滑过渡的要求，避免了磁链突变引起的电流尖峰和转矩脉动，符合城轨车辆的控制需求。

3 仿真试验讨论

由于试验条件限制，无法进行大功率牵引电机现场试验，为了对新方法进行验证，进行了仿真试验。所采用的电机参数为：额定功率PN=4.0 kW，定子电阻Rs=1.405 Ω，转子电阻Rr=1.395 Ω，额定线电压UN=400 V，额定频率fN=50 Hz，额定转速为1 430 r/min，定子漏感Ls=5.839 mH，互感Lm=172.2 mH，极对数P=2，电机转动惯量J=0.013 1 kg·m2，给定负载转矩为8 N·m。

图7为无法过渡仿真试验波形，在速度达到过渡临界值时，从圆形向六边形磁链过渡。由于此时电压矢量无法满足顺利过渡条件，在临界速度点附近震荡，频繁的进行两种控制方式的过渡。这种情况引起了电流的畸变，产生了电流尖峰，对元器件造成较大冲击，也会引起转矩的波动，影响了乘坐舒适性和行车安全。

图7 无法顺利过渡波形

图8为无法平滑过渡仿真试验波形，由于没有考虑最优的过渡位置和电压矢量，此时仍存在速度的波动。在电流波形和转矩波形中仍存在较大的脉动，影响了元器件的使用寿命。

图8 无法平滑过渡波形

图9为综合考虑速度、磁链位置和电压矢量的新过渡方法仿真试验波形。在过渡时综合考虑了电压矢量和最佳的磁链位置，保证了磁链畸变最小。由图9可以看出，在过渡时，速度基本没有发生波动，原有控制方式发生的电流冲击和转矩脉动也大幅度减小。因此仿真试验证明，新的过渡判据是切实可行的。

图9 平滑过渡波形

4 结论

本文通过在过渡点综合考虑速度过渡条件、磁链矢量切换条件和过渡点电压矢量选择条件，与仅考虑速度过渡条件和过渡点非零电压矢量条件对比，得出如下结论：

(1)新型过渡控制策略，综合考虑速度、磁链和电压矢量的关系，在过渡时，两种控制方式的电压矢量选择规则不会冲突，能满足下一时刻的控制需求，不会造成速度和转矩的脉动。

(2)新型过渡控制策略，由于过渡时磁链的精准控制，对定子电流波形的影响极小，不会对器件耐压和通流能力造成额外的负担，因此这种过渡控制方式，具有较好的实用性。

参考文献：

[1]孟苓辉,刘志刚,刁利军,等.城轨列车牵引逆变系统可靠性评估[J].铁道学报,2014,36(9):34-38.

MENG Linghui,LIU Zhigang,DIAO Lijun,et al.Evaluation of Reliability of Urban Rail Train Traction Inverter System[J].Jouranal of the China Railway Society,2014,36(9):34-38.

[2]冯江华,陈高华,黄松涛.异步电动机的直接转矩控制[J].电工技术学报,1999,14(3):29-32.

FENG Jianghua,CHEN Gaohua,HUANG Songtao.Direct Self Control(DSC) of Asynchronous Motor[J].Transactions of China Electrotechnical Society,1999,14(3):29-32.

[3]ORTEGA C,ARIAS A,CARUANA C,et al.Improved Waveform Quality in the Direct Torque Control of Matrix-converter-fed PMSM Drives[J].IEEE Transactions on Industrial Electronics,2010,57(6):2101-2110.

[4]DEPENBROCK M.Direct Self Control(DSC) of Inverter-fed Induction Machine[J].IEEE Transactions on Power Electronics,1988,3(4):420-429.

[5]AGUIRRE M,CALLEJA C,LOPEZ-DE-HEREDIA A,et al.FOC and DTC Comparison in PMSM for Railway Traction Application[C]//Proceedings of the 2011-14th European Conference on Power Electronicsand Applications.New York:IEEE,2011:1-10.

[6]张爱玲,王震宇,杨文杰.直接转矩控制系统中减小转矩脉动方案的比较[J].电机与控制学报,2009,12(5):566-570.

ZHANG Ailing,WANG Zhenyu,YANG Wenjie.Comparison between Two Kinds of Reducing Torque Ripple of Based on Direct Torque Control[J].Electric Machines and Control,2009,12(5):566-570.

[7]李祥飞,王坚,黄济荣.全速域异步电动机的改进型直接转矩控制[J].铁道学报,2007,29(4):27-31.

LI Xiangfei,WANG Jian,HUANG Jirong.Improved Direct Torque Control for Asynchronous Motor in All Speed Range[J].Jouranal of the China Railway Society,2007,29(4):27-31.

[8]STEIMEL A.Control of the Induction Machine in Traction[J].Bochum Research Bibliography,1998(12):361-369.

[9]孟庆春,叶锦娇,郭凤仪.异步电动机直接转矩控制系统的改进方案[J].中国电机工程学报,2005,25(13):118-122.

MENG Qingchun,YE Jinjiao,GUO Fengyi.An Improved Scheme of Induction Motor Dierect Torque Control System[J].Proceedings of the CSEE,2005,25(13):118-122.

[10]倪大成,年晓红,刘可安.十八边形磁链直接转矩控制算法设计及实现[J].铁道学报,2008,30(2):28-33.

NI Dacheng,NIAN Xiaohong,LIU Kean.Design and Implementation of the 18-side Polygon Flux Linkage DTC Algorithm[J].Jouranal of the China Railway Society,2008,30(2):28-33.

[11]HU H,LI Y D,ZENG Y.Direct Torque Control of Induction Motor for Railway Traction in Whole Speed Range[C]//Conference of the IEEE Industrial Electronics Society.New York:IEEE,2002:2161-2166.

[12]侯黎明,冯晓云,王永强,等.异步牵引电机全速域直接转矩控制策略的研究[J].铁道机车车辆,2013,33(2):38-42.

HOU Liming,FENG Xiaoyun,WANG Yongqiang,et al.Research on Direct Torque Control Strategy for Asynchronous Traction Motor at Full Speed Range[J].Railway Locomotive & Car,2013,33(2):38-42.

[13]廖永衡,冯晓云,王珍.低开关频率下基于直接自控制的谐波抑制方法[J].电工技术学报,2012,27(8):126-132.

LIAO Yongheng,FENG Xiaoyun,WANG Zhen.Research on Harmonic Elimination in Low Switching Frequency Based on Direct Self Control[J].Transactions of China Electrotechnical Society,2012,27(8):126-132.

[14]张春,郭兴众,江明,等.全速范围直接转矩控制新型建模与研究[J].电子科技大学学报,2006,35(5):794-797.

ZHANG Chun,GUO Xingzhong,JIANG Ming,et al.Novel Modeling and Research of Direct Torque Control System for Whole-speed Range[J].Journal of University of Electronic Science and Technology of China,2006,35(5):794-797.

[15]陈哲明,曾京.大功率异步牵引电动机在全速范围下的直接转矩控制[J].微特电机,2010,38(1):54-60.

CHEN Zheming,ZENG Jing.Direct Torque Control for High Power Asynchronous Traction Motors in Full Speed Range[J].Small & Specia Electrical Machines,2010,38(1):54-60.

[16]范文进,冯晓云,葛兴来,等.大功率异步电动机的直接转矩控制系统优化[J].机车电传动,2008(3):24-30.

FAN Wenjin,FENG Xiaoyun,GE Xinglai,et al.Optimization of Direct Torque Control System for High Power Asynchronous Motor[J].Electric Drive for Locomotives,2008(3):24-30.

[17]孙艳霞,雷丹.异步电动机直接转矩控制的低速性能改善[J].大连交通大学学报,2008,29(1):56-58.

SUN Yanxia,LEI Dan.Study of Asynchronous Motor Direct-torque Control with Improved Low-speed Performance[J].Journal of Dalian Jiaotong University,2008,29(1):56-58.

[18]刘洋,史黎明,赵鲁.一种基于混合型磁链观测器的异步电机直接转矩控制[J].电工技术学报,2015,30(10):157-163.

LIU Yang,SHI Liming,ZHAO Lu.Direct Torque Control of Asynchronous Motor Based on Hybird Flux Observer[J].Transactions of China Electrotechnical Society,2015,30(10):157-163.

[19]ZHOU Y,HU Y.A Novel Direct Torque Control for Electrically Excited Synchronous Motor Drives with High Power Factor and Low Ripples in Flux and Torque[C]//Power Electronics Specialists Conference.New York:IEEE,2008:4752-4756.

[20]STEIMEL A.Direct Self-control and Synchronous Pulse Techniques for High-power Traction Inverters in Comparison[J].IEEE Transactions on Industrial Electronics,2004,51(4):810-820.

[21]高瑾,胡育文,黄文新,等.六边形磁链轨迹的无刷直流电机直接自控制[J].中国电机工程学报,2007,27(15):64-69.

GAO Jing,HU Yuwen,HUANG Wenxin,et al.The Direct Self Control of Brushless DC Motor Based on the Hexagon Locus of Stator Flux Linkage[J].Proceedings of the Chinese Society for Electrical Engineering,2007,27(15):64-69.