考虑车辆周转的铁路动态货运服务网络设计优化模型及其分支-定价-切割算法

王保华，何世伟

(1. Amazon Research，北京 100024；2.北京交通大学 交通运输学院，北京 100044)

铁路货运服务网络设计属于战术规划层次的决策内容，主要目标是制定一个货运列车开行方案，包括列车始发和终到站(以及甩挂站)、开行频率、编组内容等，力求在一定服务水平的基础上满足客户的运输需求。铁路动态货运服务网络设计在此基础上进一步引入时间维度，根据列车开行频率以及列车间车流接续关系规定了各列车的具体开行时段，可作为列车开行方案与列车运行图的中间过渡环节，为编制列车运行图奠定良好基础。货物列车的组织开行需要充足的动力(机车)和装载设备资源(车辆)作保障，二者的合理运用是货运服务网络能够高效率、低成本满足客户运输需求的基础。如果决策者能够在优化设计货物服务网络的同时考虑机车车辆资源的合理周转，既可以使当前已经投入使用的机车和车辆资源发挥最大效力，也可以避免由于机车、车辆资源不足导致日常运输组织无法正常开展。

尽管众多学者对货运服务网络设计进行了广泛的研究[1-21]，但与铁路相关的研究仍然相对较少。文献[3]把铁路货运列车开行方案问题构建为一个混合整数规划模型，考虑列车最大编组辆数和车站中转能力限制等约束，目标在于最小化列车开行费用、车小时费用、车辆中转费用。该文给出一种基于Lagrangian的对偶调整算法用于求解模型，并基于美国铁路运输企业的实际案例对模型和算法进行了测试。文献[4]基于动态需求构建列车编组和空车调整综合优化模型，目标在于最小化列车开行费用、中转费用以及相关延误和惩罚费用。该文给出一种基于分解策略的启发式算法，并在由4个车站及5条双向线路组成的网络中进行了测试。文献[8]以满足客户服务水平为目标，研究铁路货运列车开行方案问题，并将遗传算法和禁忌搜索算法结合起来对模型进行了求解。文献[17]研究了快捷货物运输动态服务网络的设计问题，主要以铁路运输为例给出了优化模型和求解算法，并分析了该模型和算法在公路和航空领域的通用性。文献[18]以意大利铁路为背景，将铁路货运列车开行方案问题转化为一类费用为凹函数的多商品网络流问题，并给出了一种禁忌搜索算法。

近年来也有若干学者开始研究考虑相关设备资源周转的货运服务网络设计问题，这些研究通常引入时间维度来描述资源的循环过程，在服务网络设计优化时考虑最大化这些资源的利用率。文献[7]研究公铁联运网络中的运输计划编制问题，构建了时空网络用于描述铁路平车、拖车的周转过程以及货物的移动过程。该文构建整数规划模型并给出求解算法，还进一步考虑了车站作业能力、机车周转等因素的影响。文献[14-15]研究了考虑多种资源周转的货运服务网络设计问题，该文构建了包含联弧和循环设计变量、联弧和径路货流变量的多商品网络流模型，给出了各类服务开行时间的确定方法，目标在于最小化所有货物的总运输时间。该文还考虑了空驶车辆的调配问题。文献[19]基于上文的研究给出了一种基于分支-定价的求解框架，提高了模型求解效率。

本文主要研究考虑货运车辆周转的铁路动态服务网络设计问题。首先拓展传统的离散时空网络为一类超级网络，用于描述货运车辆在网络中的流动过程(即所谓车辆流)以及在重、空两种状态中的转换，基于此构建混合整数规划模型。动态服务网络设计问题由于引入了时间因素，通常会导致网络规模较为庞大，采用商用优化模型求解软件(如IBM ILOG等)无法直接求解，而本文所研究的问题又在网络中引入了车辆流的概念，进一步增加了模型的求解难度，故本文给出一种基于分支-定价-切割的求解算法，通过动态调整货流和车辆流的径路集以减小模型规划和计算量。最后通过算例对算法进行验证。

本文所建的模型不仅适用于某单一特定车型，也适用于更为普遍的多车型场景，而单一车型(如粮食专用车、化学用品专用罐车等)可以看作是对给出模型的一种简化。本文给出的方法既可应用于中长期计划的制定，也可以用于周、日计划乃至阶段计划的编制过程。当应用于中长期计划制定时，根据给定货流结构、可用车型、各车型车辆数量和空间分布，可以得到最优列车时刻表以及列车编组计划；当用于短期计划时，编组计划可作为框架性指导，列车编组内容将严格按照编组计划规定，这将简化模型和算法的计算量，但与此同时，问题的优化空间也受一定影响。考虑到实际运营中，编组计划经常根据货流结构进行微调，本研究在应用于短期计划编制时，可以考虑适当放宽编组计划，例如只严格规定重点列车的编组内容，而允许对其他列车的编组计划进行调整，此时，模型结果也可以用于编组计划微调的参考和依据。

1 考虑车辆周转的铁路动态运输服务网络设计模型

在模型构建之前，首先对文献[17]定义的铁路动态服务网络进行拓展。该文献中的铁路动态服务网络以离散时空网络为基础，只要合理设置单位时段的长度，离散时空网络足以满足实际应用需要。在运输服务网络结构已经确定的条件下，各类车辆在网络中的流转可以看作是车辆流寻路的过程，车辆将按照一定规则分配到运输服务网络中的各条运输服务联弧(也即列车运行线)上去。与普通货流有所不同的是，车辆流在运输服务网络上的分配过程要更加灵活，有可能有特定的起点和终点，也有可能有服务区域的限制(例如，用于散粮运输专用的车辆一般都为企业自购，只能服务于部分区域)，并且运输服务联弧上的车辆流大小应与其上的货流大小相匹配。基于此，根据车辆的使用区域范围对动态离散时空网络进行区域划分，每个区域添加一个超级节点表示车辆流的虚拟起点，为所有区域添加一个超级节点表示车辆流的虚拟终点，不同区域之间通过运输服务联弧相连，如图1所示。图1中的运输服务联弧表示货运列车，其发车时间、出发站、到达时间、到达站等信息取决于联弧起点和终点的属性，延迟联弧表示车流在同一车站的停留过程，超级联弧并没有实际含义，仅代表车辆的虚拟起点和虚拟终点。车辆不同使用区域对应不同的虚拟起点和虚拟终点，车辆将从对应区域的虚拟起点出发，在该区域对应的时空网络中(整个时空网络的一部分)选择合理的径路。

图1 超级动态货运列车服务网络

1.1 参数定义

1.2 决策变量定义

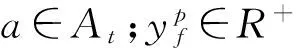
1.3 模型构建

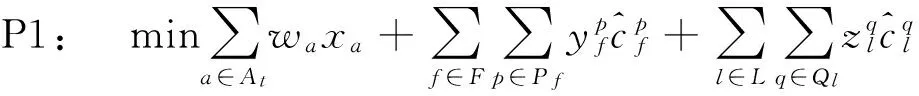
( 1 )

s.t.

∀f∈F

( 2 )

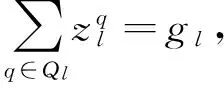
( 3 )

( 4 )

( 5 )

∀a∈Atrain，e∈E

( 6 )

xa∈{0，1}，∀a∈Atrain

( 7 )

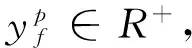
( 8 )

( 9 )

式( 1 )为目标函数，表示最小化总成本，包括添加运输服务联弧的固定成本、货流在网络中流动的成本及车辆流在网络中流动的成本；式( 2 )为货流的流量守恒约束；式( 3 )为车辆流的流量守恒约束；式( 4 )和式( 5 )为运输服务联弧上车辆流的最小值和最大值约束，其中最大值和最小值即编组计划规定的列车最大编组辆数和最小编组辆数；式( 6 )表示运输服务联弧上的总货流量应小于其上车辆流决定的最大流量；式( 7 )～式( 9 )为决策变量的逻辑约束。

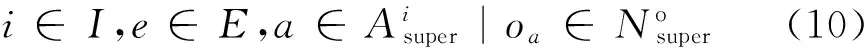
2 求解算法

首先讨论Benders割的生成方法。基于给定的服务网络设计变量xa，原模型退化为包含两类商品流(货流和车辆流)的多商品网络流问题，给出基于列生成的求解算法。

2.1 Benders割的生成方法

令运输服务网络设计变量xa(x为其向量形式)为原模型的复杂变量，τ为人工变量，可定义主问题如下

P2：

s.t.

xa∈{0，1}，∀a∈Atrain

τ≥0

令(x*，τ*)表示上述主问题的最优解的向量形式。在模型中添加人工变量m和r用于保证子问题总有解。由于服务网络设计变量x为整数变量，因此需要考虑该变量的分支过程(该变量只取0或1，因此分支过程较为简单，本文不再赘述)。给定(x*，τ*)，可构建子问题用于获取Benders割。

s.t.

∀f∈F

(13)

(14)

∀a∈Atrain

(15)

∀a∈Atrain

(16)

m|F|+|L|+2|Atrain|+a+e-n≤0 ∀a∈Atrain，e∈E

(17)

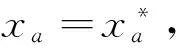
(18)

xa∈{0，1}，∀a∈Atrain

(19)

(20)

(21)

mj≥0，i=1，2，…，2|Atrain|+

|Atrain||E|+|F|+|L|

(22)

r>0

(23)

以上模型可以用下文介绍的列生成法求解。令(y*，z*，m*，l*)表示子问题的最优解，β为式(18)的对偶向量，M表示一个足够大的正数，原模型最优目标函数值的上界为

原模型最优目标函数值的下界为

如果|ωupper-ωlower|≤ε，不需要再向模型中添加Benders割，否则，在上文中的主问题中添加如下Benders割

2.2 求解子模型的列生成算法

上述子问题属于一类特殊的多商品网络流问题，其中车辆流和货流的可选径路集大小决定了模型的规模。当网络规模较大时，显然采用先获取货流和车辆流所有径路，然后再求解模型的方法并不可取。为此，本文给出一种列生成算法，通过不断求解定价子问题，来增加货流和车辆流的径路，此即定价过程。

2.3 算法总体步骤

综上，求解模型P1的分支-定价-切割算法步骤如下，易知该算法在足够长的时间内可收敛至全局最优解，可根据实际需要设置算法终止条件，如连续若干次迭代目标函数值无改进、算法运行时间达到给定标准或算法迭代到一定次数。

步骤1定义主问题P2，采用分支-定界方法求解；

步骤2采用列生成算法求解给定主问题结果后退化而得的模型P3，直至货流和车辆流都不需要再添加新径路；

步骤3根据步骤1的结果生成Benders割，并计算模型P1的上界和下界；

步骤4如果上界和下界的差距在容许范围内，算法结束，输出最优解；否则，在模型P2中添加Benders割，并采用分支-定界方法求解，转步骤2。

3 算例分析

本章将给出算例对上述模型和算法进行验证，算法由Java实现，并在操作系统为Redhat Linux 5.6、主频为Intel Xeon(E5520，2.27 GHz)的IBM System X服务器上运行。算例中的铁路物理网络如图2所示，图2中标出了各场站间列车行驶时间，单位为时段，总决策时间长度为12个时段。算例中只考虑棚车一种车辆。

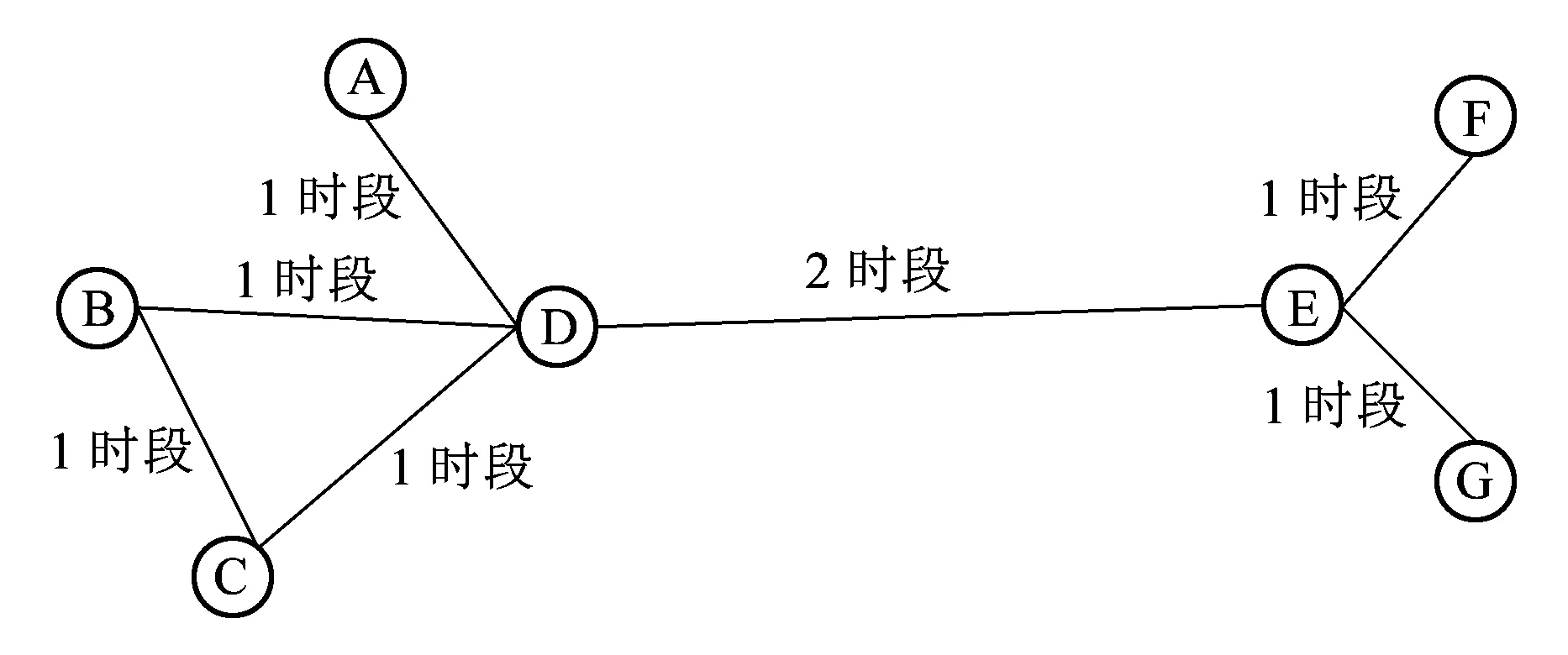
图2 算例中的铁路物理网络

备选运输服务相关参数见表1。在网络中添加运输服务联弧的固定费用(也即开行列车的固定费用)主要包括开行列车占用运行线的费用及机车牵引费用，车辆流通过网络的费用主要指租用车辆的费用(按使用时间收费)。

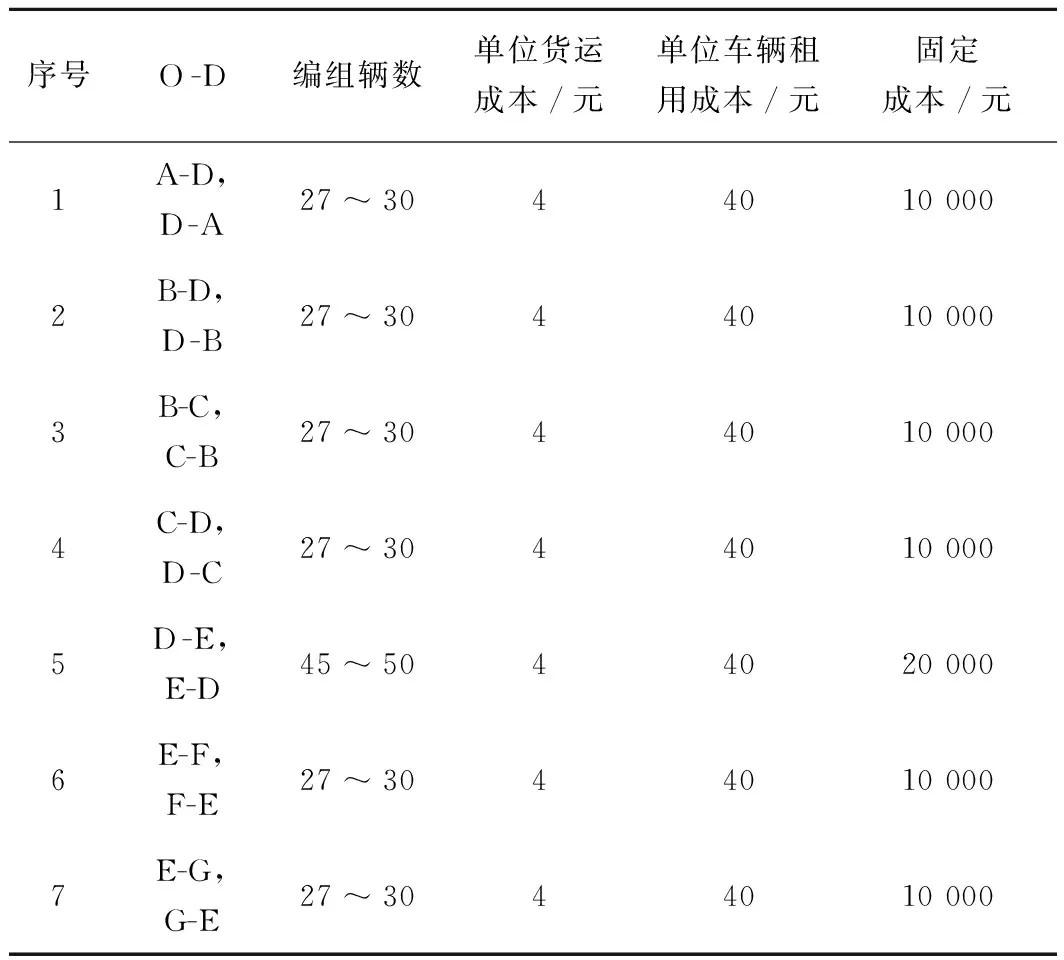
表1 备选运输服务集合

假设上述运输服务在所有时段都可开行，则可添加到网络中的备选运输服务联弧数量为130条。算例中所有货流相关参数见表2。

表2 货流相关参数

假设所有车站都属于同一区域，因此只需在离散时空网络中添加一个超级节点。再假设有1 000辆棚车可以在该区域使用，这些车辆全部保有在虚拟的超级起点。在本算例的运行环境下，算法运行2 s后收敛至最优解，见表3。注意表3中部分列车实际为重空混编，如序号为2、4和6的列车，这主要是由于模型中规定了列车最小编组辆数，由于重车数量不足，因此用空车补齐，这也是实际运营调度指挥中经常使用的一种策略。

表3 算法运行结果

在以上算例中，如果假设铁路线路D-E连接两个不同的国家，也即从A、B、C、D站出发的棚车在决策时间结束时必须返回A、B、C、D中任意一个车站，而从E、F、G站出发的棚车在决策时间结束时也必须返回E、F、G站中任意一个车站。此时，离散时空网路中将添加2个超级起点，分别对应于A、B、C、D站和E、F、G站，车辆流也将因此被拆分为两支。此外，再将E、F、G站可用的棚车数量降低为30，A、B、C、D站可用的棚车数量降低为500，以测试本文模型给出的空车调配方案。在同样的计算环境下，算法运行结果表明，在E、F、G三站间开行的列车编组中包含来自A、B、C、D站的车辆，例如，时段1开行的列车E-F(服务于货流13)，时段6开行的列车E-G(服务于货流15)和时段9开行的列车E-G(服务于货流16)。但这些车辆全部编往一列从G站开往E站的排空列车输送回A、B、C、D站所属的区域。

如果进一步把A、B、C、D站可使用的棚车数量减少到300，时段6和时段9开行的列车E-G仍由来自A、B、C、D站的车辆组成，但时段1和3开行的列车E-F则由来自E、F、G站的车辆组成。为了满足车辆使用区域的约束，时段10和12将开行两列从G到E的排空列车，时段2将开行从F到E的排空列车，用于时段开行的列车E-F。

4 结束语

本文研究考虑车辆周转的铁路动态运输服务网络设计问题，对传统的离散时空网络进行拓展以描述重车和空车之间的转化关系，建立混合整数规划模型以同时解决列车开行时段、编组内容和空车调配方案等问题。本文给出的方案既可用于进一步编制列车运行图的框架，同时也可用于估算为满足运输需求所需各车种货车的数量。文中给出了一种分支-定价-切割算法用于求解模型，该算法可保证收敛至模型的全局最优解，并给出了算例以证明模型算法的有效性。算例中还通过调整模型中的输入参数以测试不同车辆数量下排空策略的调整方案。未来进一步研究可关注当单位时段缩小(如1 h或0.5 h)导致网络规模进一步扩大时，如何改进分支-定价-切割的策略以加快算法收敛速度，满足实际应用的需要。

参考文献：

[1]MAGNANTI T L,WONG R T.Network Design and Transportation Planning:Models and Algorithms[J].Transportation Science,1984,18(1):1-15.

[2]CRAINIC T G,ROUSSEAU J.Multicommodity,Multimode Freight Transportation:A General Modeling and Algorithmic Framework for the Service Network Design Problem[J].Transportation Research Part B:Methodological,1986,20(3):225-242.

[3]KEATON M H.Designing Optimal Railroad Operating Plans:Lagrangian Relaxation and Heuristic Approaches[J].Transportation Research Part B:Methodological,1989,23(6):415-431.

[4]HAGHANI A.Formulation and Solution of a Combined Train Routing and Makeup,and Empty Car Distribution Model[J].Transportation Research Part B:Methodological,1989,23(6):433-452.

[5]FARVOLDEN J M,POWELL W B.Subgradient Methods for the Service Network Design Problem[J].Transportation Science,1994,28(3):256-272.

[6]AYKIN T.Lagrangian Relaxation Based Approaches to Capacitated Hub-and-spoke Network Design Problem[J].European Journal of Operational Research,1994,79(3):501-523.

[7]NOZICK L K,MORLOK E K.A Model for Medium-term Operations Planning in an Intermodal Rail-truck Service[J].Transportation Research Part A:Policy and Practice,1997,31(2):91-107.

[8]GOEMAN M F.Santa Fe Railway Uses an Operating-plan Model to Improve Its Service Design[J].Interfaces,1998,28(4):1-12.

[9]KIM D,BARNHART C,WARE K,et al.Multimodal Express Package Delivery:A Service Network Design Application[J].Transportation Science,1999,33(4):391-407.

[10]CRAINIC T G.Service Network Design in Freight Transportation[J].European Journal of Operational Research,2000,122(2):272-288.

[11]CHEUNG W,LEUNG L C,WONG Y M.Strategic Service Network Design for DHL Hong Kong[J].Interfaces,2001,31(4):1-14.

[12]BARNHART C,KRISHNAN N,KIM D,et al.Network Design for Express Shipment Delivery[J].Computational Optimization and Applications,2002,21(3):239-262.

[13]AGARWAL R,ERGUN O.Ship Scheduling and Network Design for Cargo Routing in Liner Shipping[J].Transportation Science,2008,42(2):175-196.

[14]ANDERSON J,CRAINIC T G,CHRISTIANSEN M.Service Network Design with Management and Coordination of Multiple Fleets[J].European Journal of Operational Research,2009,192(2):377-389.

[15]ANDERSON J,CRAINIC T G,CHRISTIANSEN M.Service Network Design with Asset Management:Formulations and Comparative Analyses[J].Transportation Research Part C:Emerging Technologies,2009,17(2):197-207.

[16]王保华,何世伟,宋瑞,等.综合运输体系下快捷货运网络流量分配优化模型及算法[J].铁道学报,2009,31(2):12-16.

WANG Baohua,HE Shiwei,SONG Rui,et al.Multi-modal Express Shipment Network Routing Optimization Model and Algorithm[J].Journal of the China Railway Society,2009,31(2):12-16.

[17]王保华,何世伟,宋瑞,等.快捷货运动态服务网络设计优化模型及其算法[J].铁道学报,2009,31(5):17-22.

WANG Baohua,HE Shiwei,SONG Rui,et al.Optimization Model and Algorithm of Dynamic Express Shipment Service Network Design[J].Journal of the China Railway Society,2009,31(5):17-22.

[18]LULLI G,PIETROPAOLI U,RICCIARDI N.Service Network Design for Freight Railway Transportation:The Italian Case[J].Journal of Operational Research Society,2011,62(12):2107-2119.

[19]ANDERSON J,CHRISTIANSEN M,CRAINIC T G,et al.Branch and Price for Service Network Design with Asset Management Constraints[J].Transportation Science,2011,45(1):33-49.

[20]申永生.综合运输体系下货运服务网络设计优化问题的研究[D].北京:北京交通大学,2012.

[21]王保华,何世伟.综合运输体系下快捷货物运输网络资源配置优化模型及算法[J].铁道学报,2017,39(2):10-16.

WANG Baohua,HE Shiwei.Resource Planning Optimization Model and Algorithm for Multi-modal Express Shipment Network[J].Journal of the China Railway Society,2017,39(2):10-16.