一种新型基于模型的动车组牵引逆变器开路故障诊断方法

胡轲珽，刘志刚，胡冉冉，林双双，高 松

(1.西南交通大学 电气工程学院，四川 成都 610031；2.四川电力设计咨询有限责任公司，四川 成都 610016)

我国的动车组均采用交流传动技术，而在交流传动系统中，机车从接触网取流之后，通过整流器整流、逆变器逆变得到交流电机所需的三相交流电。其中任一环节的故障都可能引起严重的安全事故，因此牵引逆变器的可靠运行是动车组安全高效运行的前提。CRH3型动车组采用电压型两电平逆变器，主要由6个绝缘栅双极型晶体管IGBT(Insulated Gate Bipolar Transistor)组成。文献[1]研究得出，在交流调速系统中，有82.5%的故障是由功率器件故障引起的。IGBT故障主要分为短路故障及开路故障。由于IGBT短路故障存在时间极短，很难用算法完成诊断，因而一般采用硬件电路来处理[2-3]。然而在IGBT的开路故障发生后，电机仍可以在异常状态下运行一段时间，若不及时处理，可能导致严重的后果[4]。

目前，有很多方法用于处理IGBT的开路故障，主要分为基于时频分析的方法和基于时域的方法。基于时频分析的方法主要有模糊小波算法[5]、小波神经网络算法[6]、小波支持向量机[7]和基于模型的人工神经网络诊断方法[8]等。基于时域的方法主要有电流轨迹法[9]、混合逻辑动态模型[10]、输出电流功率法[11]等。但是时频变换计算复杂，电流轨迹法易受噪声干扰，混合逻辑动态模型的诊断性能受到残差阈值设定的影响，这些因素限制了上述方法的诊断性能。

基于模型诊断MBD(Model-based Diagnosis)利用系统物理模型，建立系统各工作参数间的函数关系，研究各种故障模式导致的参数变化趋势，建立系统故障诊断模型，具有解释能力强、精确性高等优点[12]。但是基于模型诊断的方法需要建立系统精确的数学模型，对于非线性系统来说,建立其数学模型是极其困难的。文献[13-15]引入了键合图，基于模型诊断来解决系统非线性问题。文献[13]将键合图用于HXD2型机车法维莱制动系统的建模，文献[14]将键合图用于五箱系统的建模，文献[15]利用键合图建立了液体火箭发动机的模型。上述文献均是在建立诊断对象的键合图模型后，推导出相应系统的解析冗余关系ARRs(Analytical Redundancy Relationships)，建立故障特征矩阵，将系统的实际观测特征与其对比，得到诊断结果。该方法只能诊断单一故障，并且可能无法定位某些故障。

针对上述问题，本文基于模型诊断思想提出一种新型的CRH3型动车组牵引逆变器故障诊断方法。该方法同样以键合图为手段，建立非线性牵引逆变器的数学模型。与以往MBD方法不同的是，该方法从键合图中推导出符合能量守恒的系统行为约束方程。该方程在正常以及故障情况下都是成立的，基于这些约束方程，利用最小二乘法对系统当前的行为进行辨识。将辨识得到的系统行为与预期的系统行为进行对比，得到诊断结果。

1 基础知识

1.1 CRH3型动车组逆变器

CRH3型动车组牵引逆变器拓扑结构如图1所示，逆变电路由6个带反向并联二极管的IGBT组成，是一个电压型的两电平逆变器。通过将整流器输出的直流电逆变成三相交流电对牵引电机进行供电。负载为异步电机，本文将其等效为三相RL负载以及三相反电动势。

图1 CRH3型动车组牵引逆变器拓扑结构

1.2 键合图基本知识

键合图BG(Bond Graph)是以能量守恒定律为分析依据，由一些基本元件以一定的连接方式，用规定的符号表示系统功率的传输、储存、耗散等的一种分析工具。文献[16]利用键合图对电动汽车中非线性的斩波器建立基于键合图的仿真模型，获得了较为理想的结果。文献[17]对boost升压电路进行了键合图建模，利用全模式故障特征矩阵以及一致性向量对故障元件进行了检测以及定位。文献[18-19]建立了电液转向系统的键合图模型，并通过FDI方法实现了故障的诊断与评估。可以看出，键合图在对非线性系统的建模方面有其独特的优势，因而本文采用键合图对牵引逆变器进行建模。

键合图用规定的符号表示系统的基本元件，并且按照一定的规则进行连接。每个子系统或者元件之间的能量传递是通过“通口”实现的，能量传递的媒介称为“键”，是一条含有半箭头的通口线，箭头方向即为能量流动方向。电系统中的变量与键合图中的广义变量对应关系见表1。

表1 电系统中的变量与BG中的广义变量对应关系

“因果划”是在“键”末端与“键”垂直的一条线段，用于区分系统中的输入变量和输出变量。共流节点“1”和共势节点“0”用于构建键合图的拓扑。“1”节点相当于电路中的串联，与之相连的流变量相等，流入的势变量之和与流出的势变量之和相等。“0”节点相当于电路中的并联，与之相连的势变量相等，输入的流变量之和等于输出的流变量之和。

图2为共流节点和共势节点，对于共流节点来说，有

( 1 )

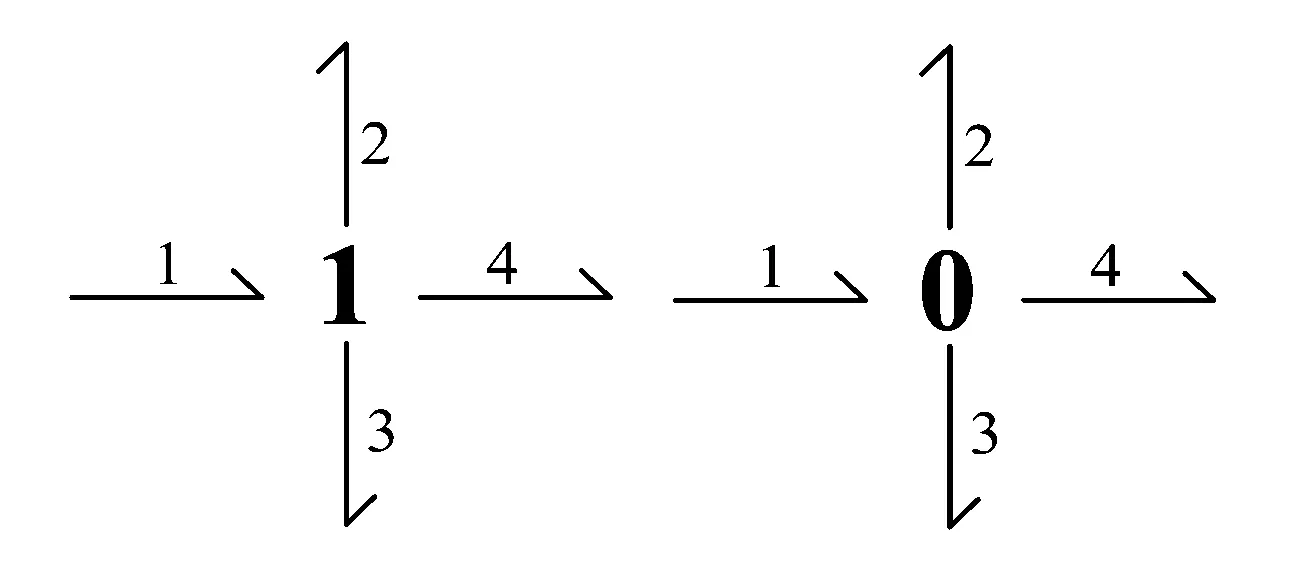
图2 共流节点和共势节点

对于共势节点来说，有

( 2 )

除此之外，还有势源Se、流源Sf、惯性元件I、容性元件C、阻性元件R、变换器TF以及回转器GY等元件。

2 牵引逆变器键合图及系统行为约束方程

2.1 逆变器的键合图模型

键合图最早用于连续系统的建模分析，但是对于连续和离散事件共存的混杂系统中开关的建模尚无统一方法，目前主要有可调制变换器描述法[20]、开关功率节点描述法[21-22]、理想开关法[23]以及由Biswas和Mosterman提出的受控节点法。本文采用受控节点法对IGBT进行建模，该方法将IGBT等效成一个受控的节点。IGBT导通时，受控节点的行为和一般的节点一致；当其关断时，受控1节点的流变量变为零，受控0节点的势变量变为零。

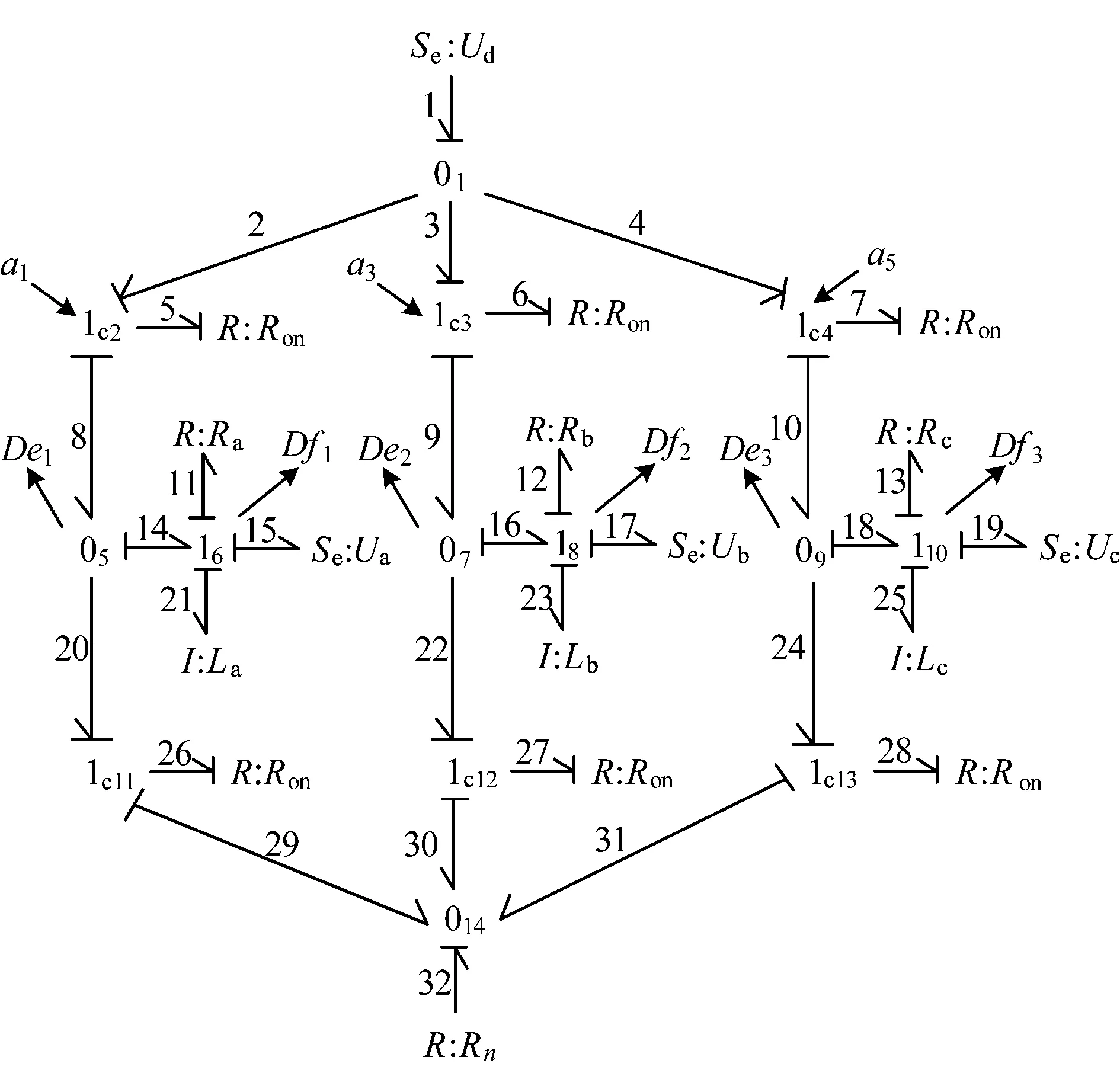
图3 牵引逆变器的键合图模型

逆变器的键合图模型如图3所示，下面以A相为例进行说明。01共势节点表示连接直流电源正端和三相桥臂的节点；受控节点1c2表示T1；Ron表示IGBT导通时的内阻；05表示A相上下桥臂之间的节点；16表示电机的等效负载支路；De1为势传感器，检测8、14、20号键上的势变量；Df1为流传感器，检测11、15、21号键上的流变量；受控节点1c11表示T4；014为连接直流电源负端与三相桥臂的节点；Rn为虚拟的接地电阻。电能从直流电源，通过节点01流入1c2。当a1给出关断信号时，电能无法流入1c2；当a1给出导通信号时，电能部分消耗于T1内阻，部分流入05。流入05的能量部分流入电机等效负载Ra、La以及ea，部分流入节点1c11。当a4给出关断信号时，能量无法流入1c11；当a4给出导通信号时，能量部分消耗于T4内阻，部分流入地下。

2.2 系统行为约束方程

基于模型诊断由Reiter在文献[24]中提出，其最初的思想为依据系统的模型以及输入，通过逻辑推理推导出系统在正常情况下的预期行为；将观测得到的实际行为和预期行为进行对比，如果两者存在差异，说明系统故障；经逻辑推理可以得到具体故障元件。

本文的诊断对象为IGBT，其预期行为，即其应导通还是关断，可由相应控制器给出。而其实际行为，即其当前是导通的还是关断的，可以通过推理得到。因此，本文将Reiter的基于模型诊断概念与文献[13-15]所用MBD方法结合，利用系统行为约束方程对当前的系统行为进行辨识，与系统预期行为进行对比，完成诊断。

系统行为约束方程是指由已知变量构成的、系统在任意条件下都满足的约束关系。这里的已知变量包括系统输入、量测量以及元件的物理参数等。系统行为约束方程一般表示为

Fl(θ，De，Df，u)=0l=1，2，…，m

( 3 )

式中：m为系统行为约束方程个数；θ为元件物理参数；De为势传感器；Df为流传感；u为系统输入。

下面给出从混杂系统BG模型得到系统行为约束方程的一般步骤：

步骤1定义一个布尔变量ai用于表示受控节点的通断状态。

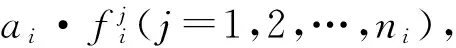
步骤3任意选择一个节点，无论是否是受控节点。利用式( 1 )以及式( 2 )建立等式，并通过BG图的因果路径消去未知变量，如果等式中所有的未知变量都可以被消去，则该等式即为一个系统行为约束方程。

步骤4重复步骤3直至所有节点都完成上述操作。

以节点05为例进行说明，对于该共势节点，根据式( 2 )有

a1f8=f14+a4f20

( 4 )

其中

( 5 )

可以得到该节点的系统行为约束方程为

( 6 )

同理可以得到07节点的系统行为约束方程为

( 7 )

09节点的系统行为约束方程为

( 8 )

式( 6 )～式( 8 )为系统行为约束方程约束系统的行为，式( 6 )～式( 8 )约束了系统中各个IGBT当前的导通状态。

3 牵引逆变器故障诊断

3.1 故障诊断原理

文献[13-15]是根据故障发生后系统的实际行为和预期行为的不一致来进行诊断的，即通过判断ARRs是否成立来对系统进行故障诊断。ARRs与系统行为约束方程类似，但是只有在系统正常时成立。故障发生后，故障元件相应的ARRs会产生残差，因而不同的故障将导致不同的残差组合，基于此建立故障特征矩阵。在获取实际的故障特征(一致性向量)之后，通过对比故障特征矩阵就可以对故障元件进行定位。其缺点在于只能完成单一故障诊断，并且可能存在不可隔离(即无法定位)的故障。

本文利用系统行为约束方程进行当前行为的识别从而完成故障诊断。由于系统行为约束方程是系统在任何情况下都满足的，因而即使在故障情况下，也可以通过量测量来完成当前系统行为的辨识。如观测到式( 6 )中当前的De1以及Df1后，可以得到当前的a1以及a4。类似地，可以得到所有IGBT当前的状态。将每个IGBT的当前状态与控制器所产生的脉冲信号进行对比，可以产生每个IGBT的残差，从而得到逆变器的故障识别向量。具体步骤如图4所示。

图4 CRH3型动车组牵引逆变器故障诊断

(1)依据键合图的建模规则，建立牵引逆变器-电机系统键合图模型，其中开关器件的建模方法为受控节点法。

(2)根据所建立的逆变器-电机系统键合图模型，对每个受控节点定义相应的布尔变量，并对每个节点建立能量守恒等式，消去未知变量后得到系统行为约束方程。

(3)在得到系统行为约束方程的基础上，利用传感器的信息，通过最小二乘法对当前系统行为进行辨识。

(4)将辨识得到的结果实时与控制系统给出的预期事件进行对比，得到蕴含故障信息的故障残差向量，完成诊断。

本文中的故障识别向量与文献[13-15]中的一致性向量存在着本质的区别。一致性向量的维度由ARRs个数所决定，并且根据某个一致性向量是否唯一来判断与其对应的故障是否可隔离，即该故障是否可以被诊断出来。因而其只能完成单一故障的诊断，并且可能会有不可被隔离的故障。本文故障识别向量的维度由IGBT个数所决定，包含了每个IGBT的残差信息，因而在理论上可以准确地诊断出任意个数IGBT的故障。

3.2 当前系统行为辨识方法

考虑到系统行为约束方程是一直被满足的，可利用式( 9 )进行当前系统行为的辨识。

( 9 )

其中

F=[F1(a)F2(a)F3(a)]T

(10)

a=[a1a2a3a4a5a6]T

(11)

当式(11)表示当前系统行为时，式( 9 )等于零。否则必然存在不被满足的系统行为约束方程，从而使式( 9 )不为零。但是考虑到外界干扰以及测量误差，在这里将式( 9 )转化为

s.t.ai=0或1i=1，2，…，6

(12)

由于本文进行的是开路故障诊断，因而认为同一桥臂的两个开关信号不会同为1，即

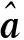
图5 当前系统行为辨识流程

3.3 故障残差向量

在对当前系统行为进行辨识之后，就可以通过基于模型诊断方法进行诊断。定义故障识别向量为

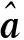
4 仿真验证及分析

在SIMULINK平台搭建CRH3型动车组牵引逆变器仿真模型，如图6所示。图6中SVPWM调制部分产生控制IGBT通断的脉冲信号；故障产生部分用0代替原脉冲信号，用于产生开路故障；当前系统行为辨识通过3.2节所述方法实现。传感器从逆变电路采集信息之后送入当前系统行为辨识部分用于计算当前系统行为。同时将其与由SVPWM调制部分产生的脉冲信号作差，得到实时的残差信号，进而完成故障诊断。

仿真参数为：直流电压3 000 V，参考电压峰值1 500 V，频率50 Hz，负载为鼠笼型异步电机，采用SVPWM调制方式。为与文献[11]进行比较，故障设置情况与其相同，分别为：T1在0.28 s时故障，T1、T4(文献[11]中T2)在0.28 s同时故障，T1、T3在0.3 s同时故障。T1在0.3 s发生故障，其电流波形与各故障识别向量如图7所示。T3发生故障之后，虽然Δa1上升，得到T1故障的信号，但是Δa4也相应地改变。从图8可以看出，在T1开路之后，在电流正半波时，D4续流的情况与正常情况时不同。在正常情况下，当上半桥臂关断、下半桥臂开通时，由D4续流。这意味着在系统行为辨识时，得到的结果是正确的。而在故障情况下，下半桥臂的开关状态与续流情况不同步，这使得系统行为辨识结果产生误差，正是这一误差使得Δa4不为零。但是该误差是将原本关断的IGBT误认为是开通的，从残差公式式(14)来看，产生的残差是负的，然而对于IGBT开路情况来说，产生的残差是正的，因此，这不会影响该方法的诊断结果。

图6 仿真示意图

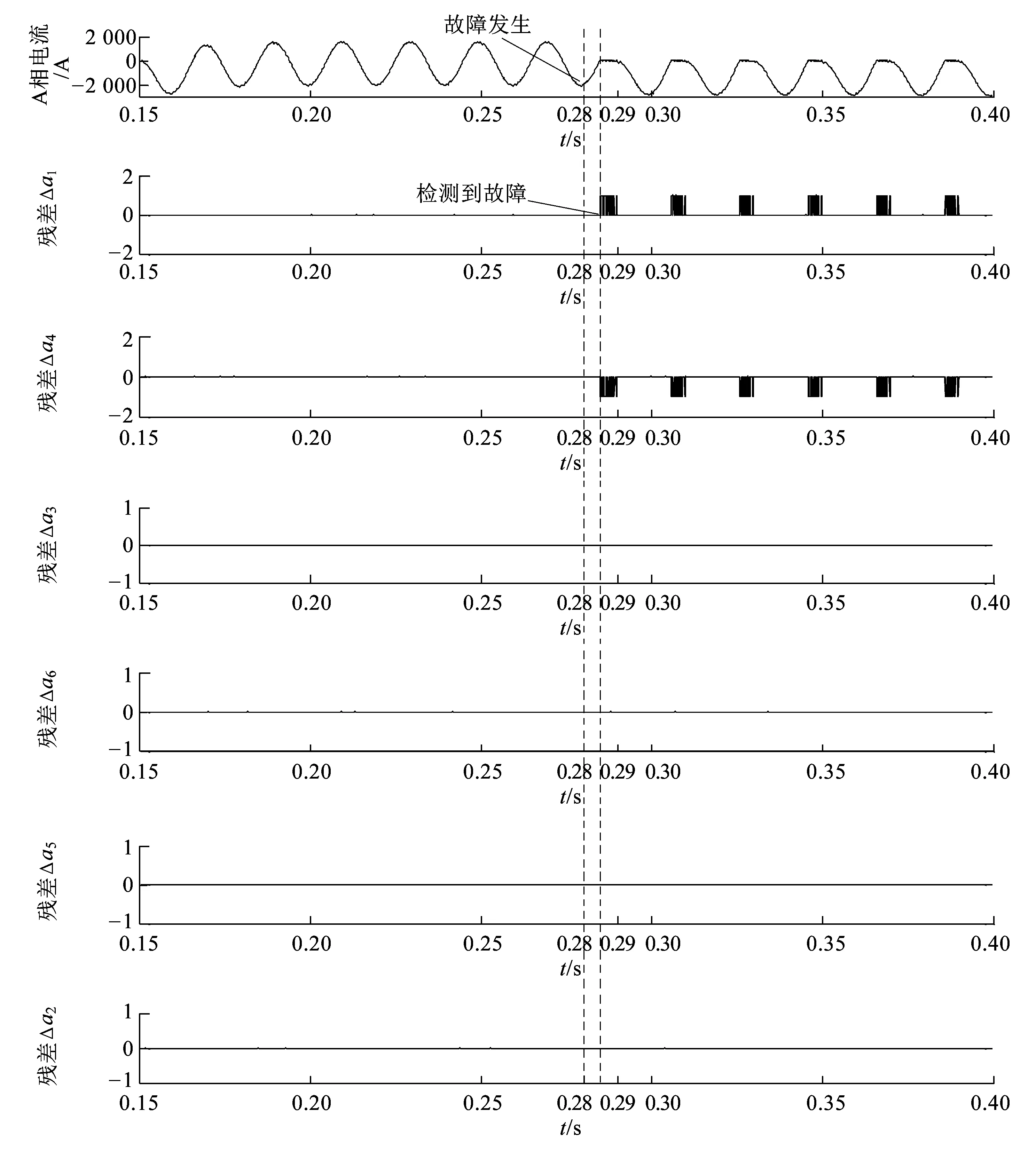
图7 T1故障时电流波形与故障识别向量

(a)正常情况下

(b)故障情况下图8 T1故障时A相下桥臂电流波形

T1以及T4在0.28 s同时发生故障时的电流波形与故障识别向量如图9所示。T1以及T3同时发生故障时电流波形与故障识别向量如图10所示。

图9 T1以及T4同时故障电流波形与故障识别向量

图10 T1以及T3同时故障时电流波形与故障识别向量

本文所设置的故障情况与文献[11]相同，两种方法诊断时间对比见表2。可以看出，本文提出的诊断方法诊断效率比文献[11]高。

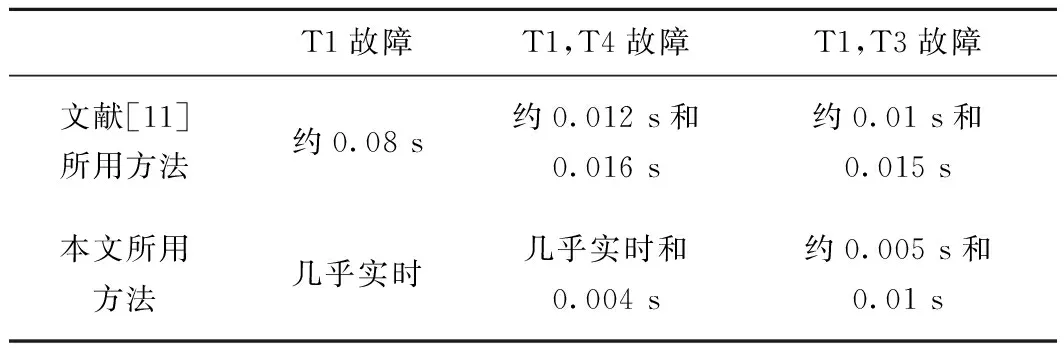
表2 本文方法与文献[11]方法诊断时间对比

5 讨论

在图7中，T1发生故障后，相应的故障识别向量可以马上做出反应，将故障识别出来。在图9中，T1在0.28 s发生故障，但是直到0.284 s左右才被诊断出来。在图10中，T1以及T3在0.3 s发生故障，T1故障在0.305 s左右被诊断出来，T3故障在0.31 s被诊断出来。以图10中T3故障的检测为例说明产生这一现象的原因。当故障发生时，观察B相电流可以发现，虽然T3在0.3 s时发生故障，但是电流波形并未发生变化。在A相电流处于负半波时，主要通过T6输出电流，D3进行极少的续流。由于D3的续流，令系统行为辨识得到了T3仍在导通的结论，从而导致在电流正半波时未能诊断出T3开路。而当A相电流处于正半波时，D3不再续流，系统行为辨识结果正确，因而可以得到正确的诊断结果。由此可知本方法的诊断时间在半个周期之内。

需要注意的是，本文中提到的开路是指由器件破裂、绑定线断裂或者焊接脱落等原因造成的故障。在这种情况下，与IGBT反并联的二极管仍然可以续流。通过之前的分析可以知道，该二极管的续流将导致诊断时间有零到半个周期的延迟。而对于由IGBT以及反并联二极管同时烧毁的开路情况，二极管不再续流。可以预见在这种情况下，故障发生后可以立刻得到诊断结果，而不会有延迟。

6 结论

针对动车组牵引逆变器中IGBT的开路故障，提出一种基于模型和事件辨识的IGBT开路故障诊断方法。利用键合图推导基于能量守恒的系统行为约束方程，完成系统行为辨识，得到诊断结果。该方法具有以下优点：

(1)具有快速诊断的能力，能在故障发生后的半个周期内完成故障识别，基本达到实时诊断。

(2)基于以能量守恒为依据的键合图模型，在逆变器的拓扑确定之后，即使在不同的控制算法以及不同的逆变器工作状态下，其诊断性能依然良好，具有较好的通用性。

(3)在多故障情况下也有良好的诊断性能。

参考文献：

[1]WIKSTROM P,TERNES L A,KOBI H.Reliability,Availability,and Maintainability of High-power Variable-speed Drive Systems[J].IEEE Transactions on Industry Applications,2000,36(1):231-241.

[2]贺虎成,张玉峰,王永宾,等.新型三相容错逆变器研究[J].电力自动化设备,2015(5):89-93.

HE Hucheng,ZHANG Yufeng,WANG Yongbin,et al.Fault-tolerant Three-phase Inverter[J].Electric Power Automation Equipment,2015(5):89-93.

[3]吴迪,伍小杰,苏良成,等.基于开绕组电机的双三电平逆变器容错控制方法[J].电力自动化设备,2014,34(4):65-71.

WU Di,WU Xiaojie,SU Liangcheng,et al.Fault-tolerant Control of Dual Three-level Inverter for Open-end Winding Induction Motor[J].Electric Power Automation Equipment,2014,34(4):65-71.

[4]于泳,蒋生成,杨荣峰,等.变频器IGBT开路故障诊断方法[J].中国电机工程学报,2011,31(9):30-35.

YU Yong,JIANG Shengcheng,YANG Rongfeng,et al.IGBT Open Circuit Fault Diagnosis Method for Inverter[J].Proceedings of the CSEE,2011,31(9):30-35.

[5]MAMAT M R,RIZON M,KHANNICHE M S.Fault Detection of 3-Phase VSI Using Wavelet-fuzzy Algorithm[J].American Journal of Applied Sciences,2006,3(1):16-42.

[6]CHARFI F,SELLAMI F,AL-HADDAD K.Fault Diagnostic in Power System Using Wavelet Transforms and Neural Networks[C]//2006 IEEE International Symposium on Industrial Electronics.New York:IEEE,2006,2:1143-1148.

[7]CUI J.Faults Classification of Power Electronic Circuits Based on a Support Vector Data Description Method[J].Metrology and Measurement Systems,2015,22(2):205-220.

[8]MASRUR M A,CHEN Z H,ZHANG B,et al.Model-based Fault Diagnosis in Electric Drive Inverters Using Artificial Neural Network[C]//Power Engineering Society General Meeting.New York:IEEE,2007:1-7.

[9]CAMPOS-DELGADO D U,PECINA-SNCHEZ J A,ESPINOZA-TREJO D R,et al.Diagnosis of Open-switch Faults in Variable Speed Drives by Stator Current Analysis and Pattern Recognition[J].IET Electric Power Applications,2013,7(6):509-522.

[10]李宁,李颖晖,朱喜华,等.基于混合逻辑动态模型和故障事件识别向量的新型逆变电路故障诊断[J].电网技术,2013,37(10):2808-2813.

LI Ning,LI Yinghui,ZHU Xihua,et al.Fault Diagnosis for New Inverter Circuits Based on Mixed Logic Dynamic Model and Incident Identification Vector[J].Power System Technology,2013,37(10):2808-2813.

[11]赏吴俊,何正友,胡海涛,等.基于IGBT输出功率的逆变器开路故障诊断方法[J].电网技术,2013,37(4):1140-1145.

SHANG Wujun,HE Zhengyou,HU Haitao,et al.An IGBT Output Power-based Diagnosis of Open-circuit Fault in Inverter[J].Power System Technology,2013,37(4):1140-1145.

[12]韩晓娟,杨锡运,刘东明,等.基于键合图理论的故障诊断方法及在锅炉给水泵上的应用[J].中国电机工程学报,2007,27(23):75-79.

HAN Xiaojuan,YANG Xiyun,LIU Dongming,et al.Research on Bond Graph Fault Diagnosis Approach and Application in Boiler Feed Water Pump[J].Proceedings of the CSEE,2007,27(23):75-79.

[13]黄志武,刘建刚,刘伟荣,等.基于解析冗余关系的法维莱制动机系统故障诊断技术[J].铁道学报,2013,35(3):29-35.

HUANG Zhiwu,LIU Jiangang,LIU Weirong,et al.Fault Diagnosis of Faiveley Braking System Based on Analytical Redundancy Relations[J].Journal of the China Railway Society,2013,35(3):29-35.

[14]王秋生,樊久铭,徐敏强,等.基于解析冗余关系的动态系统故障检测和隔离[J].哈尔滨工业大学学报,2007,39(6):924-927.

WANG Qiusheng,FAN Jiuming,XU Minqiang,et al.Dynamic System Fault Detection and Isolation with Analytical Redundancy Relations[J].Journal of Harbin Institute of Technology,2007,39(6):924-927.

[15]樊久铭,王秋生,徐敏强,等.诊断键合图在液体火箭发动机故障诊断中的应用[J].宇航学报,2007,28(4):8-15.

FAN Jiuming,WANG Qiusheng,XU Minqiang,et al.Application of Diagnosis Bond Graph to Fault Diagnosis for Liquid-propellant Rocket Engine[J].Journal of Astronautics,2007,28(4):8-15.

[16]SILVA L I,BOUSCAYROL A,DEANGELO C H,et al.Coupling Bond Graph and Energetic Macroscopic Representation for Electric Vehicle Simulation[J].Mechatronics,2014,24(7):906-913.

[17]BORUTZKY W.Bond Graph Model-based Fault Diagnosis of Hybrid Systems[M].Berlin:Springer International Publishing,2015.

[18]AROGETI S A,WANG D,LOW C B,et al.Fault Detection Isolation and Estimation in a Vehicle Steering System[J].IEEE Transactions on Industrial Electronics,2012,59(12):4810-4820.

[19]WANG D,YU M,LOW C B,et al.Model-based Health Monitoring of Hybrid Systems[M].Berlin:Springer International Publishing,2013.

[20]DAUPHIN-TANGUY G,ROMBAUT C.Why a Unique Causality in the Elementary Commutation Cell Bond Graph Model of a Power Electronics Converter[C]//Systems,Man and Cybernetics,IEEE International Conference on Systems Engineering in the Service of Humans’,Conference Proceedings.New York:IEEE,1993:257-263.

[21]UMARIKAR A C,UMANAND L.Modelling of Switching Systems in Bond Graphs Using the Concept of Switched Power Junctions[J].Journal of the Franklin Institute,2005,342(2):131-147.

[22]JUNCO S,DIEGUEZ G,RAMIREZ F.On Commutation Modeling in Bond Graphs[J].Simulation Series,2007,39(1):12-18.

[23]EDSTROM K,STROMBERG J,TOP J.Aspects on Simulation of Switched Bond Graphs[C]//Proceedings of the 35th IEEE Conference on Decision and Control.New York:IEEE,1996,3:2642-2647.

[24]REITER R.A Theory of Diagnosis from First Principles[J].Artificial Intelligence,1987,32(1):57-95.