某供弹系统高速传动机构磨损机理分析与预测模型

彭志凌， 张 毅， 丁明军， 郭 华

(1. 中北大学 机电工程学院， 山西 太原 030051； 2. 淮海工业集团有限公司， 山西 长治 046012)

0 引 言

高速传动机构在军民领域有着非常广泛的应用， 最典型的就是应用于射速很高的供弹系统之中[1]. 供弹系统高速传动机构作为一种精密的复杂产品， 其运动精度的可靠性是制约供弹系统能否完成任务的关键. 在高射速发射时， 传动机构运动副会由于磨损逐渐改变零部件的尺寸和形状. 磨损是相互接触并相对运动的两摩擦表面由于接触应力过大而导致表层材料不断损耗的现象[2-3]. 赵海鸣等[4]结合试验验证了基于磨粒磨损机理的滚刀磨损量预测模型. 中科院院士温诗铸[5]研究了载荷、 速度、 润滑和磨料硬度等因素对磨损影响规律， 总结出了二体磨粒磨损的规律. 吴俊等[6]利用偏最小二乘法建立了掘进参数与刀具磨损量关系的模型. 在磨损预测模型方面， 科罗拉多矿业大学建立了CSM模型[7]， 挪威科技大学建立了NTNU模型[8]. 赵河明等[9]进行了基于 ADAMS 的齿轮传动机构最大允许磨损量分析. 刘创等[10]采用神经网络的断路器传动机构进行了磨损预测. 张国伟等[11]针对某型通风隔离阀传动机构铰链副进行了磨损可靠性分析. 目前还未发现有文献专门针对供弹机构开展磨损研究. 为了确保供弹速度并提高供弹系统的可靠性， 供弹系统传动机构采用无链传输方式. 例如当某舰炮的射速从每分钟850发提高到每分钟6 000发， 由于其内部各个部件相对运动速度较大， 使供弹机构的磨损很明显， 严重的将导致卡弹、 供弹速度降低和停射等故障. 因此， 在高速传动机构磨损机理分析基础上构建磨损预测模型具有一定的理论意义和工程价值.

1 磨损可靠度

磨损可靠度(PS)是指在规定的时间和使用条件下， 运动机构磨损量在最大允许磨损范围内的概率[12-14]， 由最大允许磨损量和磨损速度决定.

不计润滑时， 滑动速度、 材料硬度和载荷等3个因素决定了材料的磨损速率. 累积的运动机构磨损量超过允许的最大磨损量时， 判为失效. 令最大允许磨损量与累积磨损量的差值为磨损安全裕量MW， 则磨损可靠度可表示为

PS=P(MW>0),(1)

MW=Wmax-Wt,(2)

式中：Wt为累积磨损量；Wmax为最大允许磨损量.

2 某供弹系统高速运动机构有限元仿真

某供弹系统传动机构中大模数齿轮材料为30CrNi2MoVA， 弹性模量P=2.1×109， 泊松比σ=0.25～0.3.

大模数齿轮的各项参数见表 1 所示.

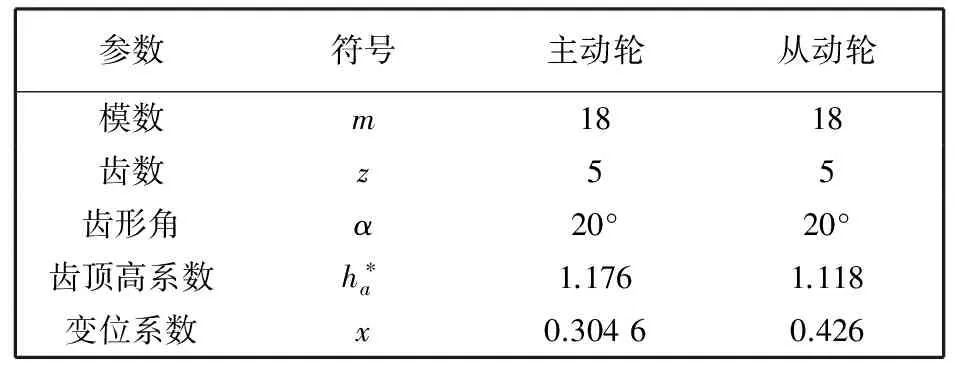
表 1 大模数齿轮的主要参数

在Pro/E中建立齿轮模型， 如图 1 所示.

图 1 齿轮模型Fig.1 Gear model

通过动力学仿真可得齿轮受力与时间的历程曲线， 如图 2 所示. 由图可知， 应力集中发生在齿廓和齿根部， 受力均值为1 923.548 N.

图 2 齿轮受力时间历程曲线Fig.2 Force curve of gear with time

3 高速传动机构摩擦磨损试验

为了获得不同影响因素下的磨损量， 开展了高速运动机构摩擦磨损试验.

根据某供弹系统高速传动机构实际情况， 本试验选用的磨损试件材料为45#钢， 试验材料的热处理工艺如表 2 所示. 对磨环结构如图 3 所示.

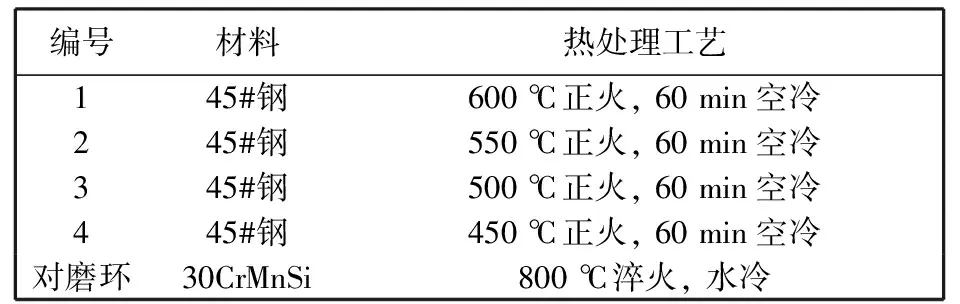
表 2 试件的热处理工艺

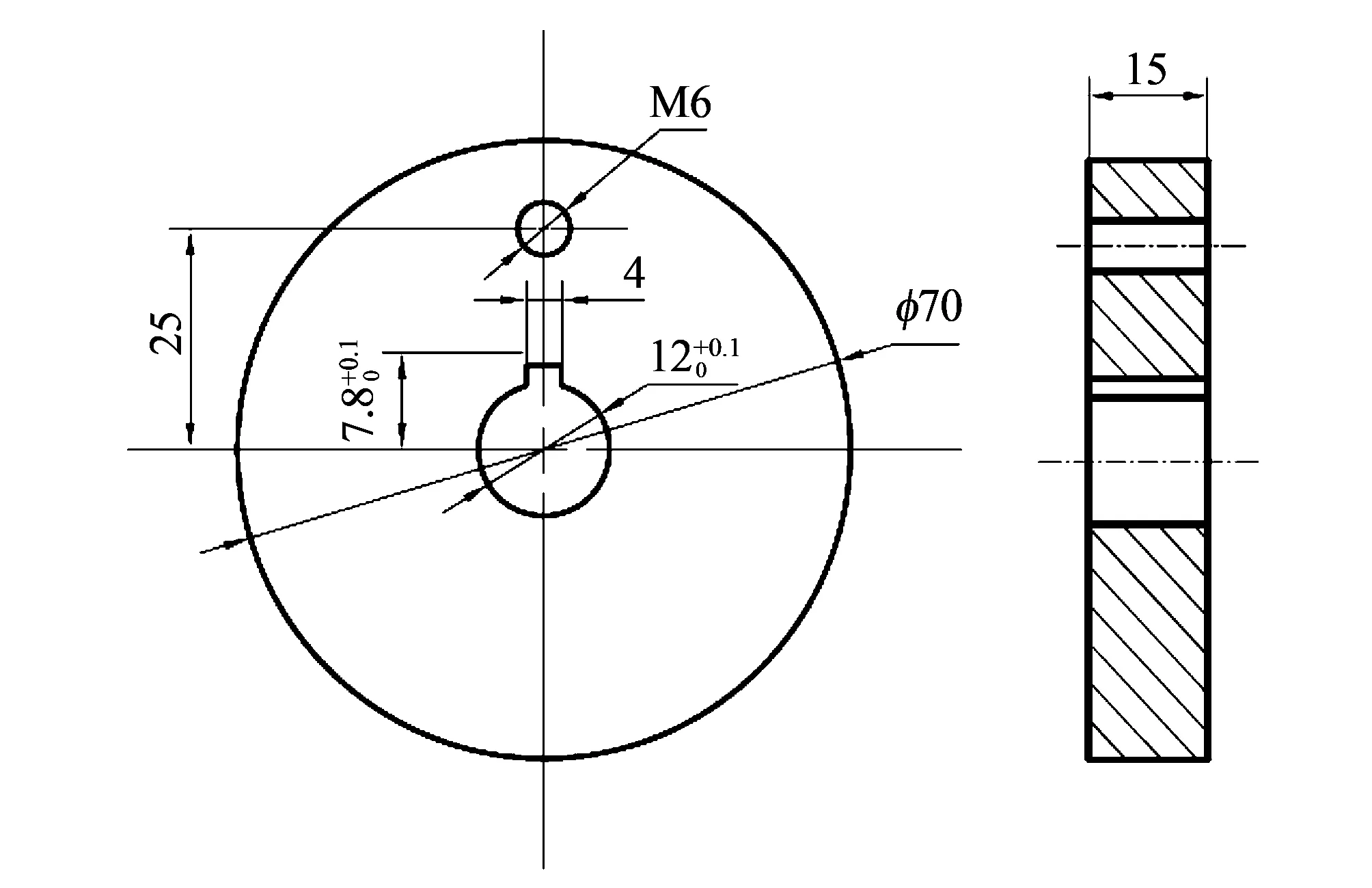
图 3 对磨环Fig.3 The grinding ring

根据某供弹系统高速传动系统中磨损副的材料、 接触力和滑动速度， 确定试验因素及其水平数如下： 表面硬度： 241, 282, 314, 366 HV等4个水平数； 载荷： 100～430 N， 分12个水平数； 转速： 50～380 r/min， 分12个水平数； 时间： 30 min. 试验方案见表 3.

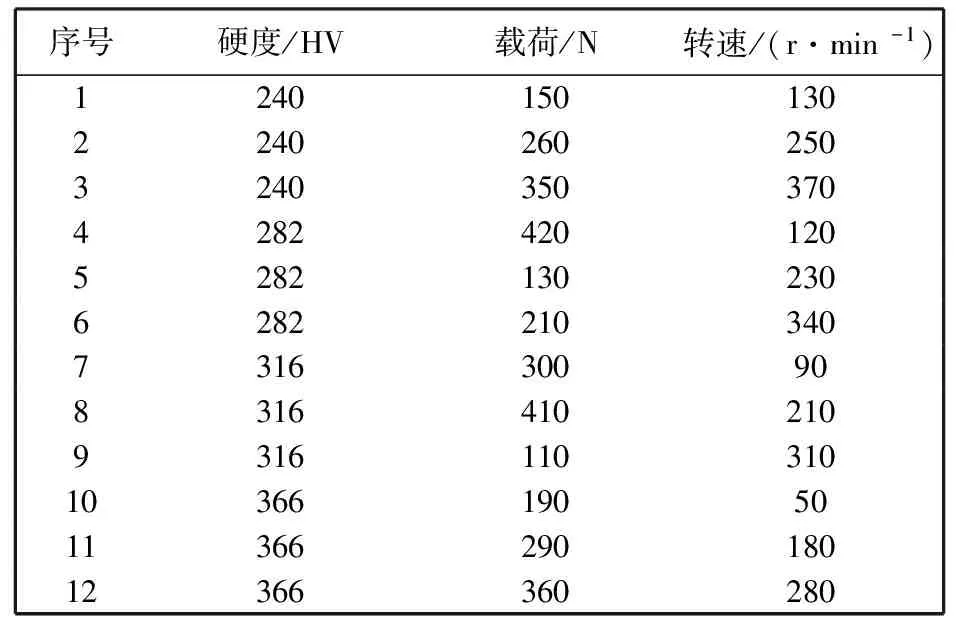
表 3 摩擦磨损方案

试验后利用显微镜观察各试件表面， 发现塑性变形较为严重， 且存在较多的磨屑， 符合粘着磨损特征， 如图 4 所示(选取载荷130 N、 转速230 r/min、 硬度282 HV为例).

图 4 磨损试验后表面微观图(N=130 N, n=230 r/min, HV=282 HV)Fig.4 Surface micrograph after wear test (N=130 N, n=230 r/min, HV=282 HV)

同时， 还观察到各试件表面有较多明显的磨痕和沟槽， 符合磨粒磨损特征， 如图 5 所示(选取载荷190 N、 转速50 r/min、 硬度366 HV为例).

图 5 磨损试验后表面微观图(N=190 N, n=50 r/min, HV=366 HV)Fig.5 Surface micrograph after wear test (N=190 N, n=50 r/min, HV=366 HV)

由此可知， 所研究的某供弹系统高速传动机构磨损是粘着磨损和磨粒磨损共同作用的结果.

4 高速传动机构磨损预测模型

鉴于磨损过程的随机性且试验数据随机误差较大， 采用均匀试验法， 并利用逐步回归法分析试验数据， 选用偏最小二乘法建立磨损量预测模型[15-19].

在建立磨损量预测模型时， 分别用x1，x2，x3表示影响磨损量的3个主要因素： 材料表面硬度、 载荷、 滑动速度.

根据均匀实验设计建立二次多项式模型

(3)

式中：a0,ai,aii,aij为回归系数；ε为随机误差；i为影响因素个数.

通过数据处理， 得到偏最小二乘法回归的二次多项式模型为

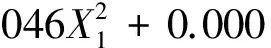
其残差平方和为4.527 8， 满足精度要求. 利用式(4)获得的磨损量预测值与试验值进行比较， 结果如表 4 所示.

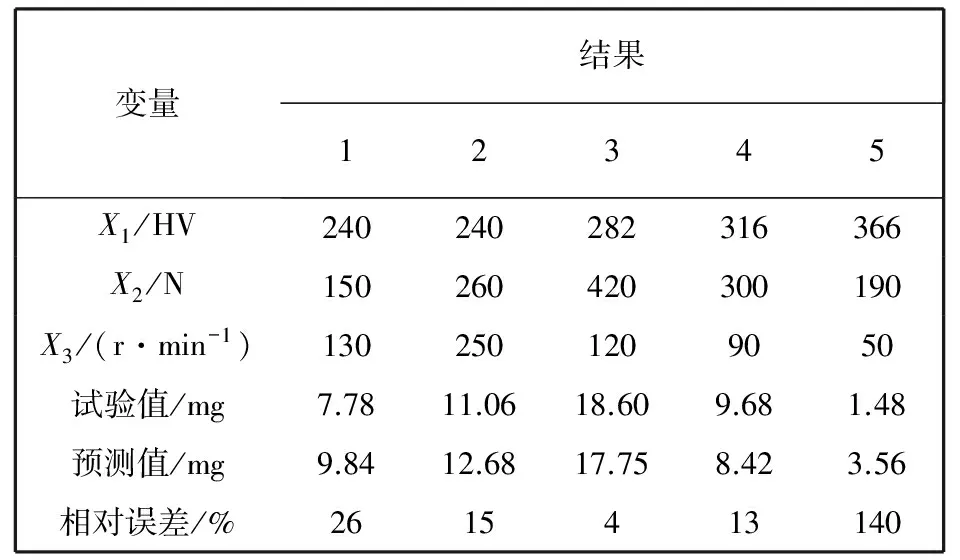
表 4 试验与预测结果

根据表 4 可知， 在该试验范围内磨损量预测的结果误差较小， 说明该磨损模型精度较好.

5 结 论

本文在分析磨损可靠度的基础上， 对某供弹系统高速传动机构进行了有限元仿真， 确定了应力集中区域及其应力平均值， 分析得出了薄弱部件. 采用均匀设计法确定试验方案， 开展不同条件下的试验， 确定了影响磨损预测模型的因素. 利用偏最小二乘法得出由材料表面硬度、 载荷、 滑动速度三因素预测磨损量的数学模型. 经与试验对比， 磨损量预测误差小， 精确度较高. 本文所采用的方法对预测磨损可靠性和寿命具有一定的理论意义和工程价值.

参考文献：

[1] 王平. 无链供弹输弹导引结构与特性分析[D]. 南京： 南京理工大学， 2009.

[2] 孙伟春. 磨粒磨损研究的现状和发展趋势[J]. 技术创新与应用， 2008(2)： 71-72.

Sun Weichun. The present situation and development trend of abrasive wear research[J]. Technical Innovation and Application, 2008(2)： 71-72. (in Chinese)

[3] 关长辉. 船用柴油机气缸套摩擦磨损机理及减磨措施分析[J]. 科技创新与应用, 2017(13)： 69-70.

Guan Changhui. The mechanism of friction and wear of cylinder liner of marine diesel engine and the analysis of wear reduction measures[J]. Technology Innovation and Application, 2017(13)： 69-70. (in Chinese)

[4] 赵海鸣, 舒标, 夏毅敏, 等. 基于磨料磨损的TBM滚刀磨损预测研究[J]. 铁道科学与工程学报, 2014, 11(4): 152-158.

Zhao Haiming, Shu Biao, Xia Yimin, et al. Study of wear prediction for TBM cutter based on abrasive wear model[J]. Journal of Railway Science and Enginerring, 2014, 11(4): 152-158. (in Chinese)

[5] 诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 1990.

[6] 吴俊, 袁大军. 大连极硬岩地层复合盾构刀具磨损的分析与预测[J]. 土木工程学报, 2015, 48(增1): 250-255.

Wu Jun, Yuan Dajun. Analysis and prediction on composite shield cutters wear in extremely hard rock in Dalian metro[J]. China Civil Engineering Journal, 2015, 48(S1): 250-255. (in Chinese)

[7] Rostami J. Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure[D]. Golden: Colorado School of Mines, 1997.

[8] Zare S, Bruland A. Applications of NTNU/SINTEF drillability indices in hard rock tunneling[J]. Rock Mechanics and Rock Engineering, 2013, 46(1): 179-187.

[9] 赵河明， 张毅， 赵意鹏. 基于 ADAMS 的齿轮传动机构最大允许磨损量分析[J]. 煤矿机械， 2015， 36(11)： 137-139.

Zhao Heming, Zhang Yi, Zhao Yipeng. Maximum allowed to wear for gear transmission mechanism based on ADAMS[J]. Coal Mine Machinery, 2015， 36(11)： 137-139. (in Chinese)

[10] 刘创， 刘宏昭. 采用神经网络的断路器传动机构磨损预测[J]. 机械科学与技术， 2017, 36(6)： 869-876.

Liu Chuang, Liu Hongzhao. Wear prediction of circuit breaker transmission mechanism based on neural network[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(6)： 869-876.(in Chinese)

[11] 张国伟， 何雪浤， 谢里阳. 某型通风隔离阀传动机构铰链副磨损可靠性分析[J]. 机械设计， 2017, 34(8)： 55-60.

Zhang Guowei, He Xuehong, Xie Liyang. Wear reliability assessment calculation of hinge pairs in the ventilation isolation value transmission mechanism[J]. Journal of Machine Design, 2017, 34(8): 55-60. (in Chinese)

[12] 吴耀庆. 树脂基复合摩擦材料摩擦磨损机理研究及有限元模拟[D]. 北京： 中国地质大学， 2013.

[13] Xu H Y. Velocity ratio theory and design principles on solid-liquid pump[C]. International Conference of Pump and Systems, Beijing, 1992： 527.

[14] 王超. 基于磨损理论的滑动导轨精度保持性预测模型研究[D]. 天津： 天津理工大学, 2015.

[15] Lubas J. Assessment and application of Ti B2coating in sliding pair under lubricationconditions [J]. Wear, 2012, 296(1)： 504-509.

[16] Lubas J. Tribological properties of surface layer with boron in friction pairs[J]. Surface Review and Letters, 2009, 16(5)： 767-773.

[17] Wang X, Kwon P Y, Schrock D, et al. Friction coefficient and sliding wear of AlTiN coating under various lubrication conditions [J]. Wear, 2013, 304(1)： 67-76.

[18] Okonkwo P C, Kelly G, Rolfe B F. The effect of temperature on sliding wear of steel-tool steel pairs [J]. Wear, 2012, 282-283(8)： 22-30.

[19] Chassaing G, Faure L, Philippon S, et al. Adhesive wear of a Ti6Al4V tribopair for a fast friction contact [J]. Wear, 2014, 320(1/2): 25-33.