不规则区域平面弹性问题的正则区域重心插值配点法

， ， ，

(1.山东建筑大学 工程力学研究所，济南 250101； 2.山东建筑大学 理学院，济南 250101)

1 引 言

求解弹性力学平面问题的主要方法有解析解法[1]和数值分析方法。对于不规则平面弹性问题，很难得到其解析解，因此需要借助数值方法进行求解。求解不规则区域平面弹性问题的数值方法计算中，有限元法[2,3]、边界元法[4]、有限差分法[5]和无网格法[6,7]是应用最广泛的方法。有限元法有其不足之处，需要进行大量网格划分，影响了有限单元法的计算精度和实际应用范围。边界元法可只对不规则边界进行离散，离散化误差仅仅来源于不规则边界，但边界元法依赖于所求问题的基本解，需要进行奇异积分计算。对于不规则问题，采用有限差分法计算，需要构造特殊的差分格式。近年来兴起的无网格法有效弥补了有限单元法、边界元法和有限差分法的不足之处。基于径向基函数法的数值方法[7]将径向基函数引入未知函数近似过程，该方法不需要划分网格,局限性在于计算精度非常依赖形状参数的选取。

配点法是一种真正意义上的无网格方法，该方法是基于微分方程强形式的离散方法，程序实施方便，无需进行网格划分。常用的配点法有拟谱法[8]和微分求积法(DQM)[9]。拟谱法是基于谱函数近似展开，数值求解微分方程的配点法。通过微分矩阵来表达未知函数的各阶导数，微分矩阵通过对未知函数的近似函数求导得到。为了提高计算精度，在拟谱法中的节点一般采用谱多项式的零点来求解。微分求积法是由Bellman和Casti在20世纪70年代提出的求解偏微分方程的一种数值计算方法，其本质是通过在全域节点的函数值加权近似得到未知函数的导数值。微分求积法的权一般通过Lagrange插值计算。拟谱方法和微分求积法不能直接应用于不规则问题的数值分析。

Lagrange插值是函数近似的重要方法，随着插值节点数量的增加，Lagrange插值表现出极大的数值不稳定性。将Lagrange插值公式改写成重心公式的形式，可以显著降低插值的数值不稳定性和改善计算精度。采用重心Lagrange插值近似未知函数的配点型方法即重心Lagrange插值配点法具有不需要划分网格、程序实施方便和计算精度高的优点，已广泛应用于求解线性和非线性微分方程的初值问题、边值问题和初边值问题[10-16]。

本文采用重心插值配点法求解不规则区域弹性平面问题。将不规则区域嵌入到规则的矩形区域，实现区域正则化。与有限单胞法相比[17]，本文方法为全局配点方法，不需要划分计算单元。在规则区域上，通过重心插值离散和施加边界条件得到规则区域上的位移数值解，利用重心插值得到不规则区域内任意节点的位移解。提出了一种研究不规则区域弹性平面问题的正则区域法，为求解不规则弹性平面问题提供了一种高精度的数值算法，通过数值算例验证了方法的有效性和计算精度。

2 重心Lagrange插值及其微分矩阵

2.1 一维重心Lagrange插值函数及其微分矩阵

对于区间[a,b]上的节点a=x1,x2,…,xn=b,函数p(x)在节点处的函数值为pj=p(xj),j= 1,2,…,n,则函数p(x)的重心Lagrange型插值函数为[16]

(j= 1,2,…,n) (1)

(m= 1,2,…)

(2)

写成矩阵的形式为

p(m)=D(m)p

(3)

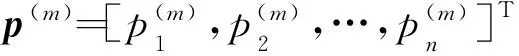
2.2 二维重心Lagrange插值函数及其偏微分矩阵

假设函数p(x,y)在定义的矩形区域Ω0= [a,b]×[c,d]上，由节点a=x1,x2,…,xm=b,c=y1,y2,…,yn=d构成Ω0上张量积型节点(xi,yj),对应的函数值pi j=p(xi,yj)。函数p(x,y)的重心Lagrange插值为[16]

(4)

式中Li(x)和Mj(y)是一维重心Lagrange插值基函数。由式(4)，函数p(x,y)的(l+k)阶偏微分可以写为

(5)

未知函数p(x,y)在节点(xi,yj),i= 1,2,…,m,j= 1,2,…,n处的(l+k)阶偏微分值为

(p= 1,2,…,m,q= 1,2,…,n)

(6)

式(8)可以用矩阵形式表示为

P(l,k)= (C(l)⊗D(k))P

(7)

式中C(l)为节点{xi}处l阶重心Lagrange插值微分矩阵，⊗为矩阵的Kronecker积，D(k) 为节点{yj}处k阶重心Lagrange插值微分矩阵。定义C(0)=Im和D(0)=In,Im和In分别为m阶和n阶单位矩阵。向量P和P(l,k)分别为函数值及其(l+k)阶偏微分值构成的列向量。

3 不规则区域弹性平面问题的正则区域重心Lagrange插值配点法

3.1 直角坐标系下弹性力学的基本方程

在直角坐标系下，平面问题的位移表达控制方程为

(8)

位移边界条件

(9)

位移形式表达的力边界条件为

(10)

3.2 不规则区域弹性平面的正则区域法

正则区域法是将任意不规则物理区域Ω嵌入到一个规则的矩形计算区域Ω0= [a,b]×[c,d],将规则区域Ω0的几何边界条件记作Γ0,不规则区域Ω的几何边界条件记作Γ。在Ω0的x方向布置m个节点x1,x2,…,xm,y方向布置n个点y1,y2,…,yn,从而可以布置成m×n的张量型数值计算节点(xi,yj),i= 1,2,…,m,j= 1,2,…,n。如图1所示，·为区域Ω内的节点，°为区域Ω0外的节点，构成计算节点。

利用插值式(4)近似位移函数u(x,y)和v(x,y),并将其代入位移控制方程(8),利用偏导数的微分矩阵表达式(7),位移控制方程(8)的重心插值配点法离散方程可写作如下矩阵形式。

(11)

引进记号

方程组(11)可化简为

LU=F

(12)

式中u,v,fx和fy分别为位移和体力函数在计算节点处函数值构成列向量。

3.3 边界条件的离散及施加

(13)

式(13)的矩阵形式为

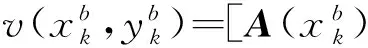
(14)

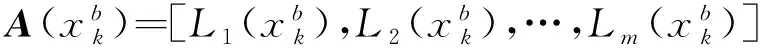
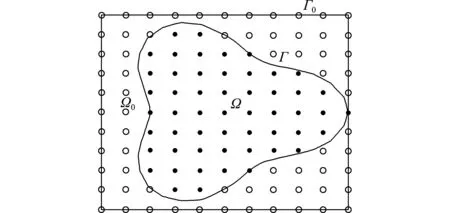
图1 不规则区域Ω嵌入一个矩形区域Ω0

Fig.1 Irregular domain Ω embedded into a rectangular regionΩ0

力边界条件(10)可采用类似的方式离散。将位移和力边界条件的离散方程，简记为

B0U=g,B1U=h

(15)

采用附加法[15,16]施加边界条件(15)，即将方程(15)附加到方程(12)，得到

(16)

方程组(16)为过约束线性方程组，采用最小二乘法求解。在数值算例实施过程中，采用MATLAB的反斜杠命令求解方程组(16)。为确保方程组(16)解的唯一性，选取的边界节点数量应大于正则区域边界点的数量。

4 数值算例

本文数值算例，采用MATLAB进行数值算例程序的编写，计算节点采用与Chebyshev节点同分布的点。不同数量节点计算的绝对误差和相对误差分别定义为Ea=‖Uc-Ue‖2,Er=‖Uc-Ue‖2/‖Ue‖2。Uc和Ue为计算值和解析解值列向量；‖•‖2表示向量的2范数。

算例1拱形区域Ω,三条直角边固支，拱顶承受面力作用，各点坐标分别为O(-1,0),B(1,0),C(1,1),D(-1,1),如图2所示。拱顶曲线函数为抛物线y= 2-x2。拱顶上的面力和体力分量由位移解析解u(x,y) =y(x2-1)和v(x,y) =y(x2-1)确定。

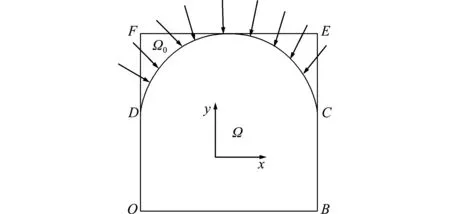
图2 拱形区域嵌入矩形区域

Fig.2 Arch domain embedded rectangular region

在本文的数值算例中，不规则区域内的插值节点采用结构化的布置方式，这有利于计算结果的可视化绘图。不同数量计算节点的计算误差列入 表1。由表1可知，采用5×5个计算节点即可达到极高的计算精度，随着计算节点数量的增加，计算精度有所降低。这是因为本算例的解为二次多项式，重心Lagrange插值为多项式插值，采用高次多项式近似低阶多项式的误差，随着近似多项式的次数增加而增大。

exp(x)(xcosy+sinx)

表1 拱形区域的位移绝对和相对误差

Tab.1 Computational errors of displacement by barycentric interpolation collocation method under different numbers of nodes in example 1

计算节点数m=n绝对误差Ea相对误差Er52.3750×10-131.0065×10-14113.4157×10-121.4476×10-13151.5458×10-106.5509×10-12212.5137×10-91.0653×10-10

表2 花瓣型区域的位移绝对和相对误差

Tab.2 Computational errors of displacement by barycentric interpolation collocation method under different numbers of nodes in example 2

计算节点数m=n绝对误差Ea相对误差Er91.3919×10-31.1896×10-5131.3971×10-71.1941×10-9171.1323×10-109.6777×10-13217.4544×10-106.3709×10-12

图3 拱形区域插值节点分布图

Fig.3 Interpolated nodes in arch domain

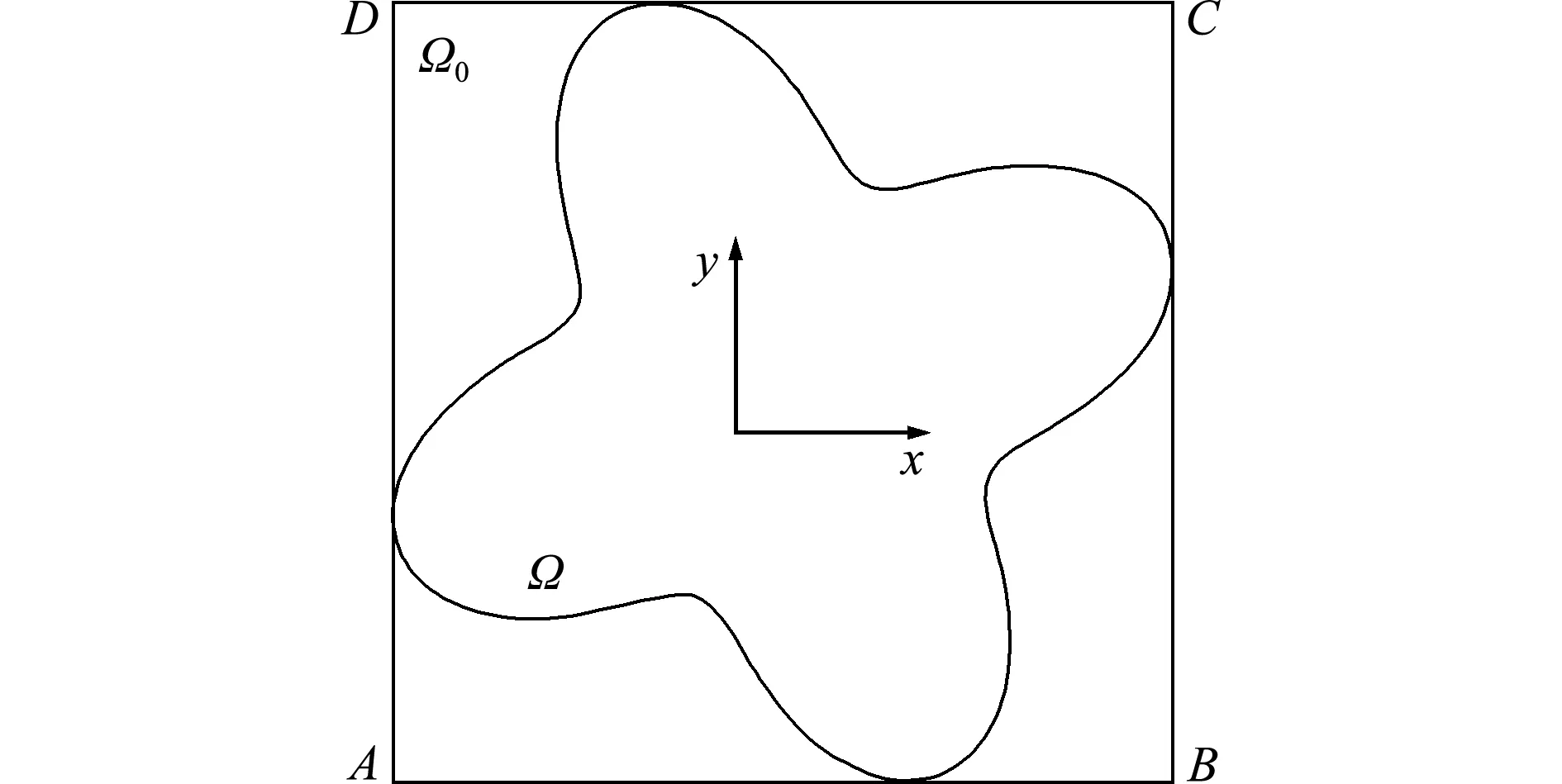
图4 花瓣型区域嵌入矩形区域

Fig.4 Petals domain embedded rectangular region

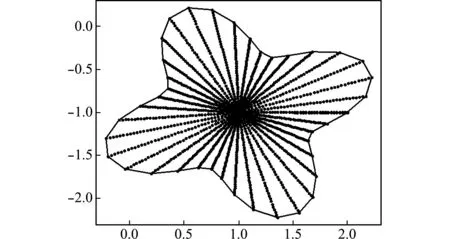
图5 花瓣型区域插值节点分布图

Fig.5 Interpolated nodes in petals domain

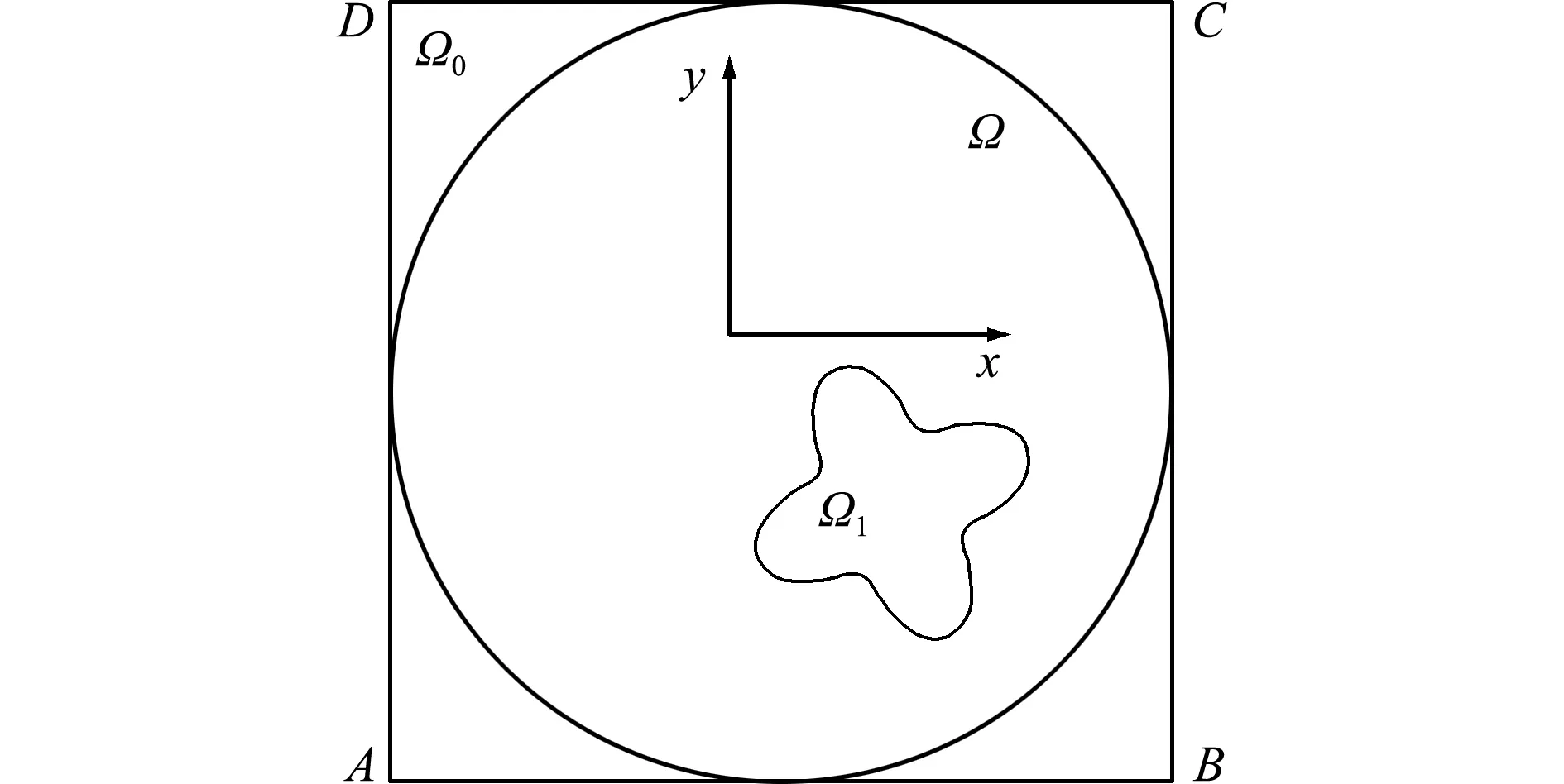
图6 含有花瓣形孔洞的圆形域嵌入矩形区域

Fig.6 Circular domain with a petal-shaped holes embedded rectangular region

算例3圆域含有花瓣型孔洞的多连通区域Ω=Ω2Ω1,如图6所示，花瓣型孔洞区域Ω1的边界曲线参数方程为

x= 1+(1+0.3sin(4θ))cosθ

y=-1+(1+0.3sin(4θ))cosθ(0≤θ≤2π)

圆形区域Ω2的边界曲线方程为x2+y2= 3.52。位移边界条件和体力分量由位移解析解确定[18]

u(x,y) = -y(2x+y)-exp(y)sin(x)+

v(x,y) = exp(y)cos(x)-xexp(x)cos(y)+

表3 圆域含有花瓣型孔洞的位移绝对和相对误差

Tab.3 Computational error of displacement by barycentric interpolation collocation method under different types and numbers of nodes in example 3

计算节点数m=n绝对误差Ea相对误差Er174.6793×10-75.8865×10-10212.5344×10-103.1883×10-13274.9887×10-106.2758×10-13295.2532×10-106.6085×10-13

图7 带有花瓣形孔洞的圆形域计算节点分布图

Fig.7 Interpolated nodes in circular domain with a petal-shaped hole

图8 含有花瓣形空洞的圆形域x方向位移数值计算等值线图

Fig.8 Contours of displacement inxdirection for circular domain with a petal-shaped hole

图9 含有花瓣形空洞的圆形域y方向位移数值计算等值线图

Fig.9 Contours of displacement in y direction for circular domain with a petal-shaped hole

5 结 论

重心插值配点法求解不规则区域上的弹性问题，具有类似谱方法的高精度。采用较少数量的节点进行计算，即可实现极高的计算精度。重心插值配点法是一种真正意义下的无网格方法，计算过程不需要背景网格的数值积分。重心插值配点法既可以求解简单的单连通区域问题，也可以求解多连通区域问题。

矩阵-向量形式表达的计算公式，极大地简化了编写计算程序的复杂性。附加法施加边界条件，就是组合离散控制方程和边界条件为过约束代数方程，该方法可以实现任意边界条件的施加。

采用正则区域法计算时，应选取包含物理区域的最小的正则区域作为计算区域。数值试验表明，采用最小的正则区域，可以提高计算精度。对于多连通域上的弹性问题，也可以采用极坐标下的正则区域法求解[13,14]。应当注意的是，在极坐标系下的正则区域为圆、扇形或环形区域。

参考文献(References):

[1] 侯祥林,李 琦,郑夕健.按位移求解弹性力学平面问题的解析构造解研究[J].计算力学学报,2015,32(3):411-417.(HOU Xiang-lin,LI Qi,ZHENG Xi-jian.Study on analytic construction solutions about solving elasticity plane problems by displacement method[J].ChineseJournalofComputationalMechanics,2015,32(3):411-417.(in Chinese))

[2] 卞正宁,杜世森,罗建辉.弹性力学问题的一阶有限元解法[J].计算力学学报,2015,32(4):544-547.(BIAN Zheng-ning,DU Shi-sen,LUO Jian-hui.First-order finite element method for elasticity[J].ChineseJournalofComputationalMechanics,2015,32(4):544-547.(in Chinese))

[3] 方锡武,贾丙辉.非匹配结点的有限单元等参插值方法及其应用研究[J].计算力学学报,2017,34(1):43-48.(FANG Xi-wu,JIA Bing-hui.Research on isoparametric interpolation for finite element with non-matching nodes and its application[J].ChineseJournalofComputationalMechanics,2017,34(1):43-48.(in Chinese))

[4] Zhang J,Qin X,Han X,et al.A boundary face method for potential problems in three dimensions[J].InternationalJournalforNumericalMethodsinEngineering,2009,80(3):320-337.

[5] Opršal I,Zahradník J.Elastic finite -difference method for irregular grids[J].Geophysics,1999,64(1):240-250.

[6] 张 雄,刘 岩,马 上.无网格法的理论及应用[J].力学进展,2009,39(1):1-36.(ZHANG Xiong,LIU Yan,MA Shang.Meshfree methods and their applications [J].AdvancesinMechanics,2009,39(1):1-36.(in Chinese))

[7] Kee B B T,Liu G R,Lu C.A least-square radial point collocation method for adaptive analysis in linear elasticity[J].EngineeringAnalysiswithBoundaryElements,2008,32(6):440-460.

[8] Weideman J A C,Reddy S C.A MATLAB differentiation matrix suite[J].ACMTransactionsonMathematicalSoftware,2000,26(4):465-519.

[9] Ma H,Qin Q H.An interpolation-based local differential quadrature method to solve partial differential equations using irregularly distributed nodes[J].CommunicationsinNumericalMethodsinEngineering,2008,24(7):573-584.

[10] Jiang J,Wang Z Q,Wang J H,et al.Barycentric rational interpolation iteration collocation method for solving nonlinear vibration problems[J].JournalofComputationalandNonlinearDynamics,2016,11(2),021001(1-13).

[11] 王兆清,庄美玲,姜 剑.非线性MEMS微梁的重心有理插值迭代配点法分析[J].固体力学学报,2015,36(5):453-459.(WANG Zhao-qing,ZHUANG Mei-ling,JIANG Jian.Nonlinear MEMS microbeam analysis by barycentric rational interpolation iteration collocation method[J].ChineseJournalofSolidMechanics,2015,36(5):453-459.(in Chinese))

[12] 王兆清,綦甲帅,唐炳涛.奇异源项问题的重心插值数值解[J].计算物理,2011,28(6):883-888.(WANG Zhao-qing,QI Jia-shuai,TANG Bing-tao.Numerical solution of singular source problems with barycentric interpolation[J].ChineseJournalofComputationalPhysics,2011,28(6):883-888.(in Chinese))

[13] 李树忱,王兆清,袁 超.极坐标系下弹性问题的重心插值配点法[J].中南大学学报(自然科学版),2013,44(5):2031-2040.(LI Shu-chen,WANG Zhao-qing，YUAN Chao.Barycentric interpolation collocation method for solving elastic problems[J].JournalofCentralSouthUniversity(ScienceandTechnology),2013,44(5):2031-2040.(in Chinese))

[14] Wang Z Q,Li S C,Ping Y,et al.A highly accurate regular domain collocation method for solving potential problems in the irregular doubly connected domains[J].MathematicalProblemsinEngineering,2014:397327.

[15] 王兆清，李淑萍.非线性问题的重心插值配点法[M].北京：国防工业出版社，2015.(WANG Zhao -qing,LI Shu-ping.BarycentricInterpolationCollocationMethodforNonlinearProblems[M].Beijing:National Defense Industry Press,2015.(in Chinese))

[16] 李树忱，王兆清.高精度无网格重心插值配点法[M].北京:科学出版社，2012.(LI Shu-chen,WANG Zhao -qing.HighAccuracyMeshlessCenterofAtta-chingMethod[M].Beijing:Science Press,2012.(in Chinese))

[17] Schillinger D,Ruess,M,Zander,N,et al.Small and large deformation analysis with the p-and B-spline versions of the finite cell method[J].ComputationalMechanics,2012,50(4),445-478.

[18] Martins N F,Rebelo M.A meshfree method for elasticity problems with interfaces[J].AppliedMathematicsandComputation,2013,219(22):10732-10745.