基于牛顿-拉夫逊的拉压不同模量问题的数值求解

*，，，

(沈阳工业大学 机械工程学院，沈阳 110178)

1 引 言

经典弹性理论的主要研究对象是具有相同拉伸和压缩弹性行为的问题。然而，在实际工程中，许多材料与结构都在不同程度上表现出拉压不同的弹性性质。材料方面，如混凝土、石墨、玻璃钢和一些高分子聚合物[1-4]等，均具有拉压不同模量；除了材料本身具有拉压不同模量的特性外，某些结构自身的构型特征决定了即便使用拉压相同模量的材料，也会具有不同拉压性质，如已经在土建及航天航空等领域得到了广泛应用的索和膜结构[5-7]。当这类问题的拉压性质相差大到一定程度时，若仍采用经典的弹性理论和有限元方法进行分析计算，会产生误差甚至是错误。综上所述，针对这类典型问题进行准确计算分析及其精密设计时，迫切需要发展基于有限元的高效数值求解方法。

Ambartsumyan[8]将拉压不同模量材料的本构关系总结为双直线模型，系统地介绍了该问题的初始假定与基本方程，在此基础上提出了拉压不同模量的弹性理论[8,9]。近年来，由于工程问题求解以及理论发展的需要，不仅解析法[1,10-13]成功地应用到某些典型问题中，而且基于有限元法的数值求解技术也得到了相应的发展。其中，杨海天等[14，15]提出了基于初应力技术的有限元迭代格式，并建立了基于连续域蚁群算法的二维拉压不同模量反问题的数值求解模型；He等[16]利用一个平面应力数值算例，测试了一种针对拉压双模量问题的加速收敛方法；张洪武等[5，17]基于参变量变分原理与共旋法，建立一种高效的求解策略，用于双模量桁架结构与张拉整体结构几何非线性行为的分析。Ding等[6,7]同样基于参变量变分原理，分析了薄膜起褶这一现象。

拉压不同模量问题究其根本为材料本构方程的不连续性，从而导致此问题具有强非线性。牛顿-拉夫逊格式因其具有收敛速度快、收敛稳定及编程简单等优点，已在ANSYS和ABQUS等大型有限元软件中成功地应用于很多非线性问题的求解，无论在理论研究还是工程应用方面，均取得很好的效果。因此，本文为了快速准确地求解拉压不同模量问题，借鉴文献[18]的策略，采用改进的Heaviside函数将材料本构方程连续光滑化，并推导连续化后的切线刚度矩阵，最后基于牛顿-拉夫逊格式进行求解，并将相应的算法应用于大规模计算问题的分析与设计中。

2 拉压不同模量问题的数值求解

2.1 拉压不同模量问题的介绍

拉压不同弹性模量问题中，主应力和主应变的关系矩阵可表示为

(1)

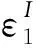
根据拉压不同模量的基本原理，柔度矩阵A的元素可表示

(2)

式中Et,μt，Ec和μc分别代表拉压弹性模量和相应的泊松比，下标t代表拉，c代表压，且假设μt/Et=μc/Ec。不难看出,拉压不同模量问题的本构方程实质是一个非连续阶梯函数,为了便于采用牛顿-拉夫逊格式进行求解，本文采用如下改进的Heaviside函数来光滑连续化这一阶梯函数。

(3)

(4)

图1 采用改进Heaviside函数近似本构方程

Fig.1 Approximated material behavior using the modified Heaviside function

式中 全应力矩阵σM可表示为

(5)

式中 相应的特征向量{l1,l2,l3}T,{n1,n2,n3}T和{m1,m2,m3}T分别为三个主方向角{α,β,γ}与初始笛卡尔直角坐标轴{x,y,z}的余弦。

与应力矩阵相对应的全应力向量为

σ= {σx x,σy y,σz z,σx y,σy z,σz x} =

{σ1,σ2,σ3,σ4,σ5,σ6}

(6)

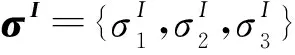
σ=TσI

(7)

相应地，全应变向量可表示为

ε= {εx x,εy y,εz z,εx y,εy z,εz x} =

{ε1,ε2,ε3,ε4,ε5,ε6}

(8)

εI=TTε

(9)

因此，将式(1,9)代入式(7)可得，全应力向量和全应变向量之间的关系为

σ=TD0TTε=D(σI)ε

(10)

式(7,9)的转轴矩阵T定义为

(11)

式中li,mi和ni(i=1,2,3)分别为式(4)特征向量的元素。

2.2 切向刚度矩阵

拉压不同模量情况下，应力的计算式(10)的张量形式为

(12)

式中 自由指标i=1,2,…,6，哑指标j=1,2,…,6，k,l=1,2,3。推导切线刚度张量，即推导式(12)关于应变张量的导数，结果如下，

(13)

第一项∂D0k l/∂εm可表示为

(14)

第二项∂Tli/∂εm可表示为

(15)

(i= 1,2,…,6) (16)

2.3 牛顿-拉夫逊求解格式

基于有限元方法的基本原理，拉压不同模量问题的非线性方程组可表示为

K(U)U=F

(17)

式中K(U)为结构整体非线性刚度矩阵，U为位移向量，F为外载荷向量。

根据牛顿-拉夫逊迭代格式，方程(17)的求解格式可表示为

ΔU=-K-1t(P-F)

(18)

式中 ΔU为节点位移增量向量，P为结构整体节点内力向量，Kt为结构整体的切线刚度矩阵。整体切线刚度阵与整体节点内力向量分别由单元切线刚度阵与单元节点内力矢量组集而成，具体计算列式如下，

(19)

式中Ket为单元切线刚度矩阵，Pe表示单元节点内力矢量，B为单元应变矩阵，ΔD为当前材料切线刚度矩阵。ΔD可依据式(13～16)进行计算，D为当前材料刚度矩阵，D可依据式(10)进行计算。

牛顿-拉夫逊迭代格式为

(2) 计算结构整体刚度矩阵K，形成结构外载荷向量F，求解KU=F。

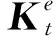
(4) 判断‖ΔU‖ <κ是否成立，成立则进行步骤(5)；否则，U=U+ΔU，回到步骤(3)。

3 算 例

算例1受水平载荷的平面应力问题

选取文献[17]的经典算例以验证本文方法的有效性。该算例属于平面应力问题，且本文均采用二维平面问题作为算例。本文所有计算公式均以三维空间问题为研究对象，只需将计算式中三维问题的矩阵与向量更换为二维问题的矩阵与向量即可。

为了形成鲜明的对比，本文采用与文献[16]相同的几何和物理参数以及有限元网格参数设置等，如图2所示，抗拉模量Et=2.2 GPa，抗压模量Ec=3.32 GPa，相应的泊松比分别为μt=0.22与μc=0.332，以满足μt/Et=-μc/Ec。

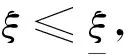
图2 受水平载荷的平面应力问题

Fig.2 Plane -stress problem under the horizontal load

分别采用文献[17]与本文方法求解图2所示有限元模型，两个方向的位移和各单元主应力的计算结果分别列入表3和表4。可以看出，本文所得解与文献[17]吻合，从而证明了本文方法的正确性。表5 给出了在选取不同控制误差时，文献[17]中所述的求解策略和本文方法所需的迭代次数。可以看出，本文方法具有良好的收敛性，且效率较高。虽然采用本文方法求解此算例所需迭代终止步数稍多于文献[17]的方法，但本文方法每一迭代步只需求解线性方程组即可，而文献[17]需要求解计算规模较大的线性互补问题，因此本文方法更加适用于大规模问题的求解。

ξ-迭代次数ux(本文)ux(文献[17])1×10-12-0.283981×1021×10-23-0.324754×1021×10-33-0.376413×102-0.425152×1021×10-44-0.406229×1021×10-55-0.415338×1021×10-66-0.425147×102

表2 迭代参数

Tab.2 Iteration parameters

ξ(初始)ξ-Z11×10-620

表3 节点位移Tab.3 Displacements of nodes

表4 单元主应力和主方向Tab.4 Principal stress and principal direction of elements

表5 不同控制误差下求解所需迭代次数

Tab.5 Iterative numbers for different control error

κ迭代次数文献[17]本文κ迭代次数文献[17]本文1×10-1361×10-711155×10-2461×10-813151×10-2581×10-914165×10-36101×10-1016161×10-36111×10-1117181×10-59141×10-1218191×10-610141×10-132022

算例2拓扑优化设计(单纯受压)

以计算规模最大拓扑优化设计问题为例，验证本文方法计算效率高和求解速率快的特性。

如图3所示，60 m×71 m的矩形结构作为初始设计区域，4个角点均约束固定。根据结构几何形式、载荷分布情况以及边界条件的对称性，本文设计时只取右半边作为设计域，中间一层单元作为非设计区域，用于承受均布的压力载荷1 kN/m。设计目标函数采用结构柔顺性最小化，以获得刚度最大化的设计，材料用量不超过整个设计域15%；抗压模量Ec=210 GPa，泊松比μc=0.3，为了避免数值奇异性，令Ec=Et/106，因此μc=μt/106，且迭代求解参数仍选用表2的数据。

如图4所示，单纯受压结构的拓扑在设计过程中的演化，仅需45步即可得到非常清晰的拓扑形式。可以看出，由于采用了单纯受压的材料模型，在整个设计过程中承载面之上的区域材料基本为空，几乎所有的材料都布置在承载面之下来承受压力。最优的拓扑形式如图5所示，设计结果为经典的下承式拱桥结构，与文献[20]中设计结果的拓扑形式基本相同。且根据表6的数据对比可知，本文所提出的方法很大程度上提高了计算效率与求解精度。

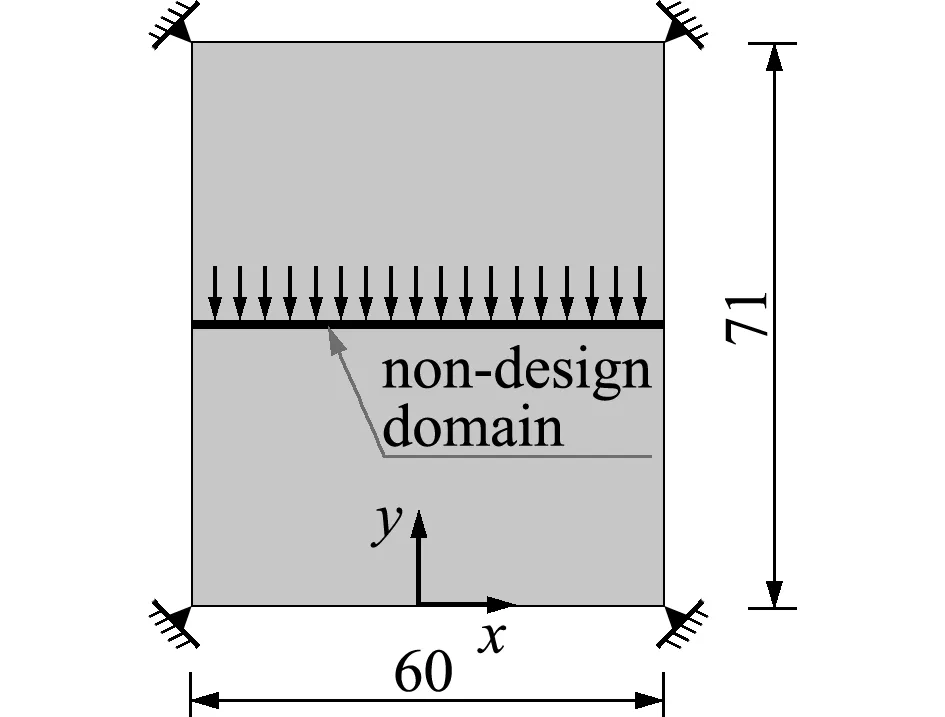
图3 初始设计区域

Fig.3 Initial design domain

图4 单纯受压结构拓扑随迭代步演化过程

Fig.4 Iteration histories of structural topology with compression-only material

图5 单纯受压结构最优拓扑

Fig.5 Optimal topologies of the structure with compression-only material obtained by using different methods

表6 不同方法所获得的计算结果

Tab.6 Results obtained by different method

方法迭代次数单步运算时间/s目标函数本文452816.84e-2文献604267.27e-2

4 结 论

本文基于牛顿-拉夫逊求解格式，提出了拉压不同模量有限元求解方法，主要策略在于光滑连续化了本构方程，在此基础上利用特征值与特征向量的求导方法推导了切线刚度矩阵的列式。数值算例证明了本文方法的正确性，并采用拓扑优化设计算例进一步验证了本文方法在稳定性和效率上的优势。

参考文献(References):

[1] Yang Q,Zheng B L,Zhang K,et al.Elastic solutions of a functionally graded cantilever beam with different modulus in tension and compression under bending loads[J].AppliedMathematicalModelling,2014,38(4):1403-1416.

[2] Khan A H,Patel B P.Nonlinear forced vibration response of bimodular laminated composite plates[J].CompositeStructures,2014,108:524-537.

[3] 魏 靖，石多奇，孙燕涛，等.拉压不同模量的缝合三明治夹芯结构梁弯曲性能[J].复合材料学报,2015,32(1):160-166.(WEI Jing,SHI Duo -qi,SUN Yan-tao,et al.Flexural properties of stitched sandwich structure beam with different modulus in tension and compression[J].ActaMateriaeCompositaeSinica,2015,32(1):160-166.(in Chinese))

[4] Iraola B,Cabrero J M.An algorithm to model wood accounting for different tension and compression elastic and failure behaviors[J].EngineeringStructures,2016,117:332-343.

[5] Zhang L,Gao Q,Zhang H W.An efficient algorithm for mechanical analysis of bimodular truss and tensegrity structures[J].InternationalJournalofMechanicalSciences,2013,70:57-68.

[6] Ding H L,Yang B G,Lou M,et al.New numerical method for two -dimensional partially wrinkled membranes [J].AIAAJournal,2003,41(1)：125-132.

[7] Ding H L,Yang B G.The modeling and numerical analysis of wrinkled membranes [J].InternationalJournalforNumericalMethodsinEngineering,2003,58：1785-1801.

[8] 阿姆巴尔楚米杨.不同模量弹性理论[M].张允真，译.北京：中国铁道出版社,1986.(Ambartsumyan S A.DifferentModulusofElasticityTheory[M].ZHANG Yun-zhen,translated.Beijing:China Railway Publishing House,1986.(in Chinese))

[9] Sun J Y,Zhu H Q,Qin S H,et al.A review on the research of mechanical problems with different moduli in tension and compression[J].JournalofMechanicalScienceandTechnology,2010,24(9):1845-1854.

[10] 赵慧玲,叶志明.拉压不同模量弹性问题[J].上海大学学报(自然科学版)，2014,20(5):550-558.(ZHAO Hui-ling,YE Zhi-ming.Elastic Bodies with different modules in tension and compression[J].JournalofShanghaiUniversity(NaturalScience)，2014,20(5):550-558.(in Chinese))

[11] He X T,Chen S L,Sun J Y.Applying the equivalent section method to solve beam subjected to lateral force and bending-compression column with different moduli [J].InternationalJournalofMechanicalSciences,2007,49(7):919-924.

[12] 吴 晓，杨立军.拉压弹性模量不同曲梁的弹性理论解[J].工程力学,2013,30(1):76-80.(WU Xiao,YANG Li-jun.The elastic theory solution for curved beam with difference elastic modulus in tension and compression[J].EngineeringMechanics,2013,30(1):76-80.(in Chinese))

[13] 张良飞,姚文娟.拉压不同模量矩形板双向弯曲问题[J].上海大学学报(自然科学版)，2017,23(1):128-137.(ZHANG Liang-fei,YAO Wen-juan.Biaxial bending of rectangular plates with different modulus[J].JournalofShanghaiUniversity(NaturalScience)，2017,23(1):128-137.(in Chinese))

[14] 杨海天,邬瑞锋,杨克俭,等.初应力法解拉压双弹性模量问题[J].大连理工大学学报,1992,32(1):35-39.(YANG Hai-tian,WU Rui-feng,YANG Ke -jian,et al.Solution to problem of dual extension-compre -ssion elastic modulus with initial stress method[J].JournalofDalianUniversityofTechnology,1992,32(1):35-39.(in Chinese))

[15] 张国庆，杨海天.蚁群算法求解二维拉压不同模量反问题[J].计算力学学报,2014,31(6):687-693.(ZHANG Guo -qing,YANG Hai-tian.Ant colony algorithm based numerical solution for inverse bimodular problems[J].ChineseJournalofComputationalMechanics,2014,31(6):687-693.(in Chinese))

[16] He X T,Zheng Z L,Sun J Y,et al.Convergence an-alysis of a finite element method based on different moduli in tension and compression[J].InternationalJournalofSolidsandStructures,2009,46(20):3734-3740.

[17] Zhang H W,Zhang L,Gao Q.An efficient computational method for mechanical analysis of bimodular structures based on parametric variational principle[J].Computers&Structures,2011,89(23)：2352-2360.

[18] 杨海天，朱应利.光滑函数法求解拉压不同弹性模量问题[J].计算力学学报，2006，23(1)：19-23.(YANG Hai-tian,ZHU Ying-li.Solving elasticity problems with bi-modulus via a smoothing technique[J].ChineseJournalofComputationalMechanics，2006，23(1)：19-23.(in Chinese))

[19] Lee I W,Jung G H.An efficient algebraic method for the computation of natural frequency and mode shape sensitivities(part I):distinct natural frequencies[J].Computers&Structures,1997,62(3):429-435.

[20] Cai K.A simple approach to find optimal topology of a continuum with tension-only or compression-only material[J].StructuralandMultidisciplinaryOptimization,2011,43(6):827-835.