非均匀Winkler弹性地基上变厚度矩形板自由振动的DTM求解

， ，

(兰州理工大学 理学院，兰州 730050)

1 引 言

变厚度板作为一种承载结构元件，在土木、海洋、机械、核工业和航空航天等工程中具有较为广泛的应用。变厚度板与等厚度板相比的优势是其能改善板结构元件的承载能力，减小其重量和几何尺寸，同时也可以改变其振动的固有频率[1]。因此，变厚度板或弹性地基上变厚度板振动问题的研究一直得到关注，已有许多研究成果[2-6]。工程实际中通常见到的弹性地基大多是均匀的[7]，但也会遇到非均匀弹性地基的情况，例如高层建筑筏基和含填充物弹性地基等。因此，对非均匀弹性地基上构件的静动力学行为进行研究是必要的。

无论是变厚度板还是非均匀弹性地基上的板，其自由振动问题的控制微分方程均是变系数偏微分方程，一般边界条件下很难求得其解析解，故目前大多采用近似方法求解，如有限元法[8]、Levy解法[9]、模态约束法[10]和Ritz法[11]等。但是上述方法中，有些需要较多的网格和较大的计算量才能达到需要的精度，有些则对边界的适用性较差。微分变换法DTM(Differential Transform Method)是一种有效的将线性或非线性微分方程变换成代数方程求解的半解析方法，最初用于对电路问题的分析[12]，近年来DTM也逐渐用于结构的静动力学响应求解，且具有较高的计算精度和计算效率，所得结果完全能满足工程方面的要求。Attarnejad等[13]采用DTM研究了转动变截面Euler-Bernoulli梁的自由振动，并给出了转速参数和锥度比对梁固有频率的影响。Kaya等[14]采用DTM分析了轴向载荷作用下闭截面复合材料Timoshenko梁弯扭耦合的振动特性，考察了弯扭耦合效应、轴向力和梁的细长比对固有频率的影响。Kaya[15]推导了旋转Timoshenko梁自由振动问题的运动控制微分方程，并用DTM进行求解，给出了轮毂半径、转动惯量、剪切变形和转速对梁固有频率的影响。滕兆春等[16]用DTM研究了弹性地基上变截面梁的自由振动。Yalcin等[17]用DTM研究了在简支、夹紧和自由边界条件下圆薄板的自由振动，并给出了具有较高精度的无量纲固有频率。Kumar[18,19]采用DTM分别分析了Winkler弹性地基上各向同性矩形板和晶体矩形板的自由振动，得出了前三阶无量纲固有频率。

本文采用DTM研究非均匀Winkle弹性地基上变厚度矩形板的自由振动特性。首先，通过经典薄板理论，推导非均匀Winkle弹性地基上变厚度矩形板自由振动的控制微分方程，并进行无量纲化。其次，通过DTM将无量纲化的控制微分方程及其边界条件转换为等价的代数方程，进行其代数方程的数值求解，并将退化后的数值结果与已有文献进行比较，验证DTM的正确性。最后，在不同边界条件下，分析地基变化参数、厚度变化参数和长宽比对矩形板无量纲固有频率的影响，并给出了非均匀Winkler弹性地基上对边简支对边固定变厚度矩形板的前六阶振型。

2 控制微分方程及参数的无量纲化

如图1所示，考虑一放置在非均匀Winkler弹性地基上的变厚度矩形板，并建立笛卡尔直角坐标系，板的长度和宽度分别为a和b，厚度为h，本文用k表示地基弹性刚度系数。

为了简化计算，该地基弹性刚度系数和矩形板的厚度只沿x方向线性变化，即

k(x) =k0[1+α(x/a)]

(1)

h(x) =h0[1+β(x/a)]

(2)

式中k0为x= 0处地基弹性刚度系数，α为地基变化参数,h0为x= 0处矩形板的初始厚度，β为厚度变化参数。

根据经典薄板理论，变厚度矩形板在非均匀弹性地基上的小振幅横向自由振动的控制微分方程为

(3)

(4)

图1 非均匀Winkler弹性地基上变厚度矩形板

Fig.1 Rectangular plates with variable thickness resting on a non-uniform Winkler elastic foundation

(5)

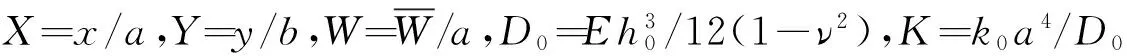
K(1+αX)W= (1+βX)Ω2W

(6)

已知，在Y= 0，Y= 1处为简支边界条件(S),于是振型函数为

W=F(X)sin(mπY)

(7)

运用式(7)，控制微分方程(6)可简化为常微分方程

K(1+αX)F=(1+βX)Ω2F

(8)

在边界X= 0，X= 1处，可为固定边界条件(C)、简支边界条件(S)或自由边界条件(F)，其无量纲边界条件分别如下。

固定(C)边界条件：

F= 0， dF/dX= 0

(9)

简支(S)边界条件：

F= 0， d2F/dX2 = 0

(10)

自由(F)边界条件：

d2F/dX2-νλ2m2π2F= 0

(11)

3 无量纲控制微分方程及边界

条件的DTM变换

本文运用DTM对非均匀弹性地基上变厚度矩形板的自由振动进行求解，首先需要将其控制微分方程和边界条件转化为等价的代数方程，具体变换规则可参考文献[12]。

运用DTM，控制微分方程(8)可变换为

(12)

式中

A0= (k+1)(k+2)(k+3)(k+4)

A1= 3β(k+1)(k+2)2(k+3)

A2= [3β2(k-1)k-2λ2m2π2+12β2k+6β2]×

(k+1)(k+2)

A3= [β3(k- 2)(k- 1)k-6βλ2m2π2k+6β3(k- 1)k-

6βλ2m2π2+6β3](k+1)

A4= [-6β2λ2m2π2(k-1)k+λ4m4π4+K-Ω2-

12β2λ2m2π2k-6νβ2λ2m2π2]

A5=- 2β3λ2m2π2(k-2)(k-1)+3βλ4m4π4-

6β3λ2m2π2(k- 1)-6νβ3λ2m2π2+αK-βΩ2

A6= 3β2λ4m4π4，A7=β3λ4m4π4

(13)

运用DTM，边界条件变换如下，

在X= 0处，

简支(S)边界条件：

(14)

固定(C)边界条件：

(15)

自由(F)边界条件：

(16)

在X= 1处，

简支(S)边界条件：

(17)

固定(C)边界条件：

(18)

自由(F)边界条件：

(19)

将式(13)分别代入边界条件式(14,17)、式(14,18)和式(14,19)，分别求解SSSS，SSCS和SSFS边界条件下的无量纲固有频率，则

(20)

式中X(n)11，X(n)12，X(n)21和X(n)22为迭代n次得到的含有未知量无量纲固有频率Ω的多项式，写成矩阵的形式为

(21)

要使式(21)有非零解，则

(22)

通过式(22)，可求得无量纲固有频率Ω。

在CSCS，CSSS和CSFS边界条件下，同理可得含有未知量无量纲固有频率Ω的特征方程，写成矩阵的形式为

(23)

在FSCS，FSSS和FSFS边界条件下，同理可得

(24)

式中

要使式(23，24)有非零解，必须有

(25)

为了控制求出的无量纲固有频率Ω的精度，有

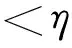
(26)

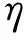
4 计算结果及分析

通过编写MATLAB程序，可获得由DTM求解非均匀Winkler弹性地基上变厚度矩形板自由振动特征值问题的无量纲频率。首先，为了验证计算方法的正确性和精度，给出了两个算例，一是Winkler 地基上矩形板的自由振动(α= 0，β= 0)；二是变厚度矩形板的自由振动(K= 0，α= 0)。然后，分析地基变化参数α、厚度变化参数β以及长宽比λ对无量纲固有基频Ω的影响。

表1 Winkler弹性地基上等厚度矩形板的无量纲基频Ω1(α =0,β =0,λ=1)Tab.1 Dimensionless fundamental frequency Ω1 for rectangular plates with constant thickness on Winkler foundations (α =0,β =0,λ=1)

表2 变厚度矩形板的前六阶无量纲固有频率Ω(K=0,α =0,λ=1)Tab.2 First six dimensionless natural frequencies Ω for rectangular plates with variable thickness (K=0, α=0,λ=1)

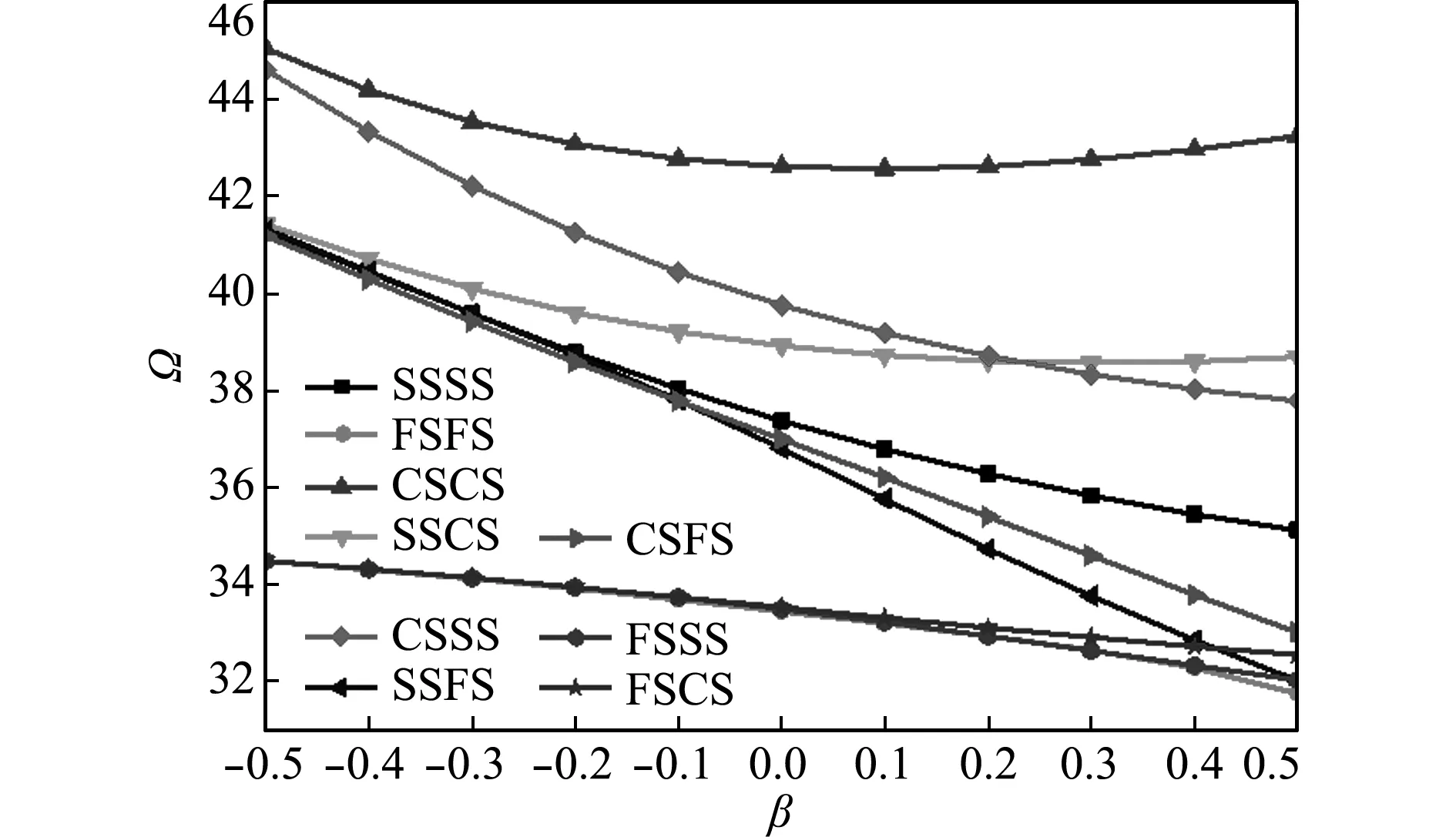
图2 不同边界条件下厚度变化参数β与无量纲固有基频Ω的关系曲线(λ=0.5，α=0.5，K=1000)

Fig.2 Dimensionless fundamental frequenciesΩversus the varied thickness parameterβfor different boundary conditions(λ=0.5，α=0.5，K=1000)

图2给出了λ=0.5，α=0.5，K=1000时，四边简支(SSSS)、对边自由对边简支(FSFS)、对边固定对边简支(CSCS)、一边固定三边简支(CSSS或SSCS)、一边自由三边简支(FSSS或SSFS) 以及一边固定一边自由对边简支(CSFS或FSCS)边界条件下，无量纲固有基频Ω与厚度变化参数β的关系曲线。可以看出，在相同参数条件下，对边固定对边简支(CSCS)的无量纲固有基频Ω最大；对边自由对边简支(FSFS) 的无量纲固有基频Ω最小；不同边界条件下无量纲基频随厚度变化参数的下降趋势越来越缓慢，但是对边固定对边简支(CSCS)和一边固定三边简支(SSCS)的无量纲固有基频随β的增大在下降后又有上升的趋势。图3分别给出了在K=1000，λ=0.5和不同α时，四边简支(SSSS)、一边固定三边简支(CSSS或SSCS)以及对边固定对边简支(CSCS)边界条件下，厚度变化参数β与无量纲基频Ω的关系曲线。可以看出，四边简支(SSSS)和一边固定三边简支(CSSS)的无量纲固有基频Ω呈现下降趋势，且随β的增大，下降趋势越来越缓慢；一边固定三边简支(SSCS)和对边固定对边简支(CSCS)的无量纲基频Ω随β的增大先下降然后缓慢上升；当K，λ和β不变时，所有边界条件下的无量纲基频Ω均随α的增大而增大。图4分别给出了在K=1000，β=0.5和不同λ时，四边简支(SSSS)、一边固定三边简支(CSSS或SSCS)以及对边固定对边简支(CSCS)边界条件下地基变化参数α与无量纲基频Ω的关系曲线。可以看出，当K，β和λ不变时，无量纲基频Ω随α的增大而增大；当K，β和α不变时，无量纲基频Ω也随λ的增大而增大。

图3 不同边界条件下厚度变化参数β与无量纲基频Ω之间的关系曲线(K=1000，λ=0.5)

Fig.3 Dimensionless fundamental frequenciesΩversus the varied thickness parameterβfor different boundary conditions (K=1000，λ=0.5)

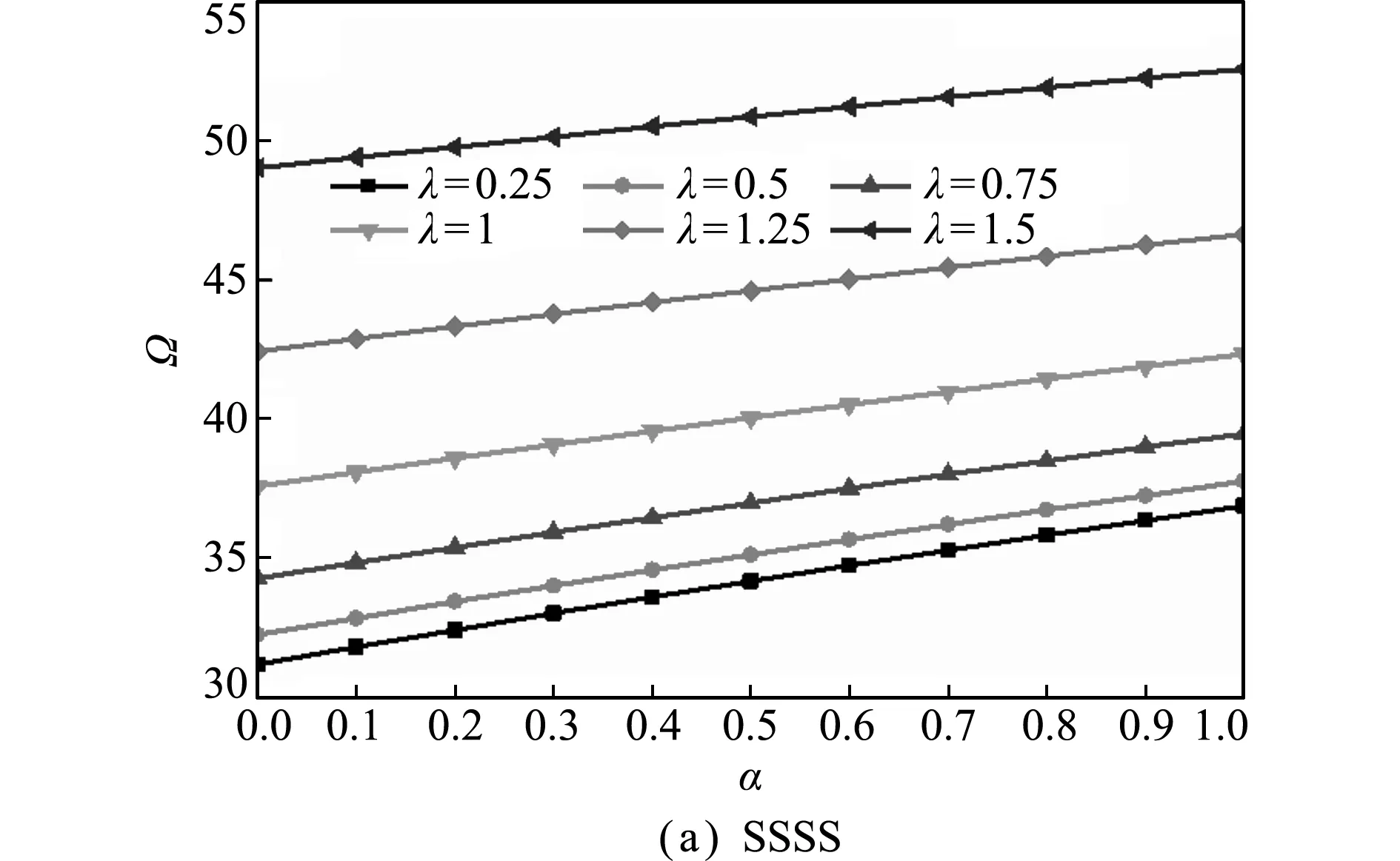
图4 不同边界条件下地基变化参数α与无量纲基频Ω之间的关系曲线(K=1000，β=0.5)

Fig.4 Dimensionless fundamental frequenciesΩversus the variable foundation parametersαfor different boundary conditions(K=1000，β=0.5)

在计算出非均匀Winkler弹性地基上变厚度矩形板的各阶无量纲固有频率Ω后，可根据无量纲固有频率Ω运用DTM反求出板的振型函数W(X,Y)=F(X)sin(mπY)。图5给出了在K=1000，ν=0.3，α=0.5，β=0.4和λ=1时，对边简支对边固定(CSCS)边界条件下非均匀Winkler弹性地基上变厚度矩形板的前六阶振型。

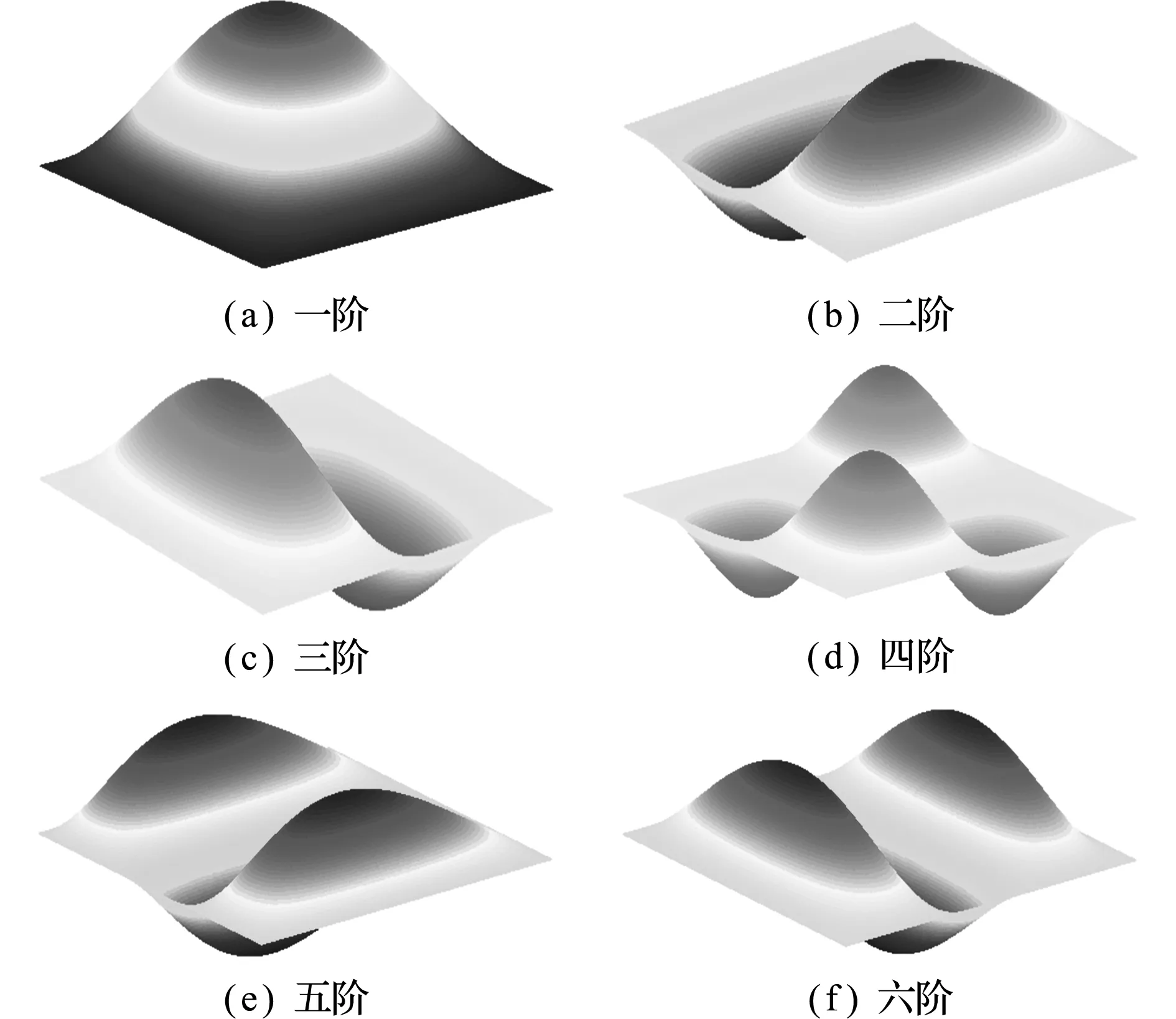
图5 对边简支对边固定板的前六阶振型

Fig.5 First six mode shapes for CSCS plates

5 结 论

本文通过运用微分变换法(DTM)研究非均匀Winkler弹性地基上变厚度矩形板的自由振动特性，并通过MATLAB编程计算出无量纲固有频率Ω。当地基变化参数α=0或厚度变化参数β=0时，将数值结果与已有文献结果进行对比，证明本文方法研究该问题可行并能达到较高的计算精度。最后，计算并分析了不同边界条件下地基变化参数α、厚度变化参数β和长宽比λ对矩形板无量纲固有频率的影响，并给出了非均匀Winkler弹性地基上对边简支对边固定(CSCS)变厚度矩形板的前六阶振型。得到以下主要结论。

(1) DTM求解非均匀Winkler弹性地基上变厚度矩形板的自由振动具有较强的适用性，又由于计算过程为代数方程的迭代求解且所选迭代误差限η值很小，故DTM的计算效率和计算结果的精度相对较高。

(2) 当无量纲地基刚度系数K、矩形板长宽比λ和地基变化参数α一定时，对边固定对边简支板(CSCS)的无量纲固有基频Ω最大；对边自由对边简支(FSFS) 的无量纲固有基频Ω最小。不同边界条件下无量纲固有频率基频Ω一般随厚度变化参数β增大而下降，且趋势越来越缓慢，但是对边固定对边简支(CSCS)和一边固定三边简支(SSCS)的无量纲基频在下降后又有上升的趋势。

(3) 四边简支(SSSS)、一边固定三边简支(CSSS或SSCS)和对边固定对边简支(CSCS)边界条件下，当无量纲地基刚度系数K和厚度变化参数β一定时，地基变化参数α越大，无量纲基频Ω越大；矩形板长宽比λ越大，无量纲基频Ω越大。

(4) 本文虽然只考虑了地基刚度系数线性变化的Winkler弹性地基上板的厚度沿单向线性变化的情况，但求解过程能完全推广用于各种边界条件下地基刚度系数任意变化的Winkler地基上厚度任意变化矩形板的自由振动问题或双参数等弹性地基上变厚度矩形板的自由振动问题，为矩形板的工程应用提供依据。

参考文献(References):

[1] 滕兆春，丁树声，郑鹏君.弹性地基上变厚度矩形板自由振动的GDQ法求解[J].应用力学学报,2014,31(2):236-241.(TENG Zhao-chun,DING Shu-sheng，ZHENG Peng-jun.Free vibration analysis of rectangular plates with variable thickness on elastic foundation by using GDQ method [J].ChineseJournalofAppliedMechanics，2014,31(2):236-241.(in Chinese))

[2] Gupta U S,Lal R.Transverse vibrations of a non-uniform rectangular plate on an elastic foundation [J].JournalofSoundandVibration,1978,61(1)：127-133.

[3] 周 叮.两对边简支变厚度矩形板横向自振频率的渐近解法[J].强度与环境,1990,2:19-25.(ZHOU Ding.The asymptotic method on natural frequencies of transverse vibration of rectangular plates with two opposite edges simply supported and varying thickness [J].Structure&EnvironmentEngineering,1990,2:19-25.(in Chinese))

[4] 王忠民,冯振宇.线性变厚度矩形薄板自由振动的精确解[J].应用力学学报,1997,14(2):114-120.(WANG Zhong-min,FENG Zhen-yu.Exact solutions for the free vibration of rectangular plates with linearly varying thickness [J].ChineseJournalofAppliedMechanics,1997,14(2):114-120.(in Chinese))

[5] Akiyama K,Kuroda M.Fundamental frequencies of rectangular plates with linearly varying thickness [J].JournalofSoundandVibration,1997,205(3):380-384.

[6] Sakiyama T,Huang M.Free vibration analysis of rectangular plates with variable thickness [J].JournalofSoundandVibration,1998,216(3):379-397.

[7] 蒲 育,滕兆春.Winkler-Pasternak弹性地基梁自由振动的二维弹性分析[J].计算力学学报，2016,33(2):182-187,201.(PU Yu，TENG Zhao -chun.Two-dimensional elastic analysis for free vibration of beams set on winkler-pasternak elastic foundations [J].ChineseJournalofComputationalMechanics,2016,33(2):182-187,201.(in Chinese))

[8] Ju F,Lee H P,Lee K H.Free vibration of plates with stepped variations in thickness on non-homogeneous elastic foundations [J].JournalofSoundandVibration,1995,183(3):533-545.

[9] Xiang Y.Vibration of rectangular Mindlin plates res-ting on non-homogenous elastic foundations [J].InternationalJournalofMechanicalSciences,2003,45(6-7):1229-1244.

[10] Horenberg J A G,Kerstens J G M.Transverse vibrations of rectangular plates on inhomogeneous foundations,part II:modal constraint method [J].JournalofSoundandVibration,1985,101(3):317-324.

[11] Laura P A A,Gutiérrez R H.Vibration of plates elastically supported on a non-homogeneous foundation [J].JournalofSoundandVibration,1984,95(4)：531-536.

[12] 赵家奎.微分变换及其在电路中的应用[M].武汉：华中理工大学出版社,1988.(ZHAO Jia-kui.DifferentialTransformationandItsApplicationforElectricalCircuits[M].Wuhan：Huazhong University of Science and Technology Press,1988.(in Chinese))

[13] Attarnejad R,Shahba A.Application of differential transform method in free vibration analysis of rotating non-prismatic beams [J].WorldAppliedSciencesJournal,2008,5(4):441-448.

[14] Kaya M O,Ozgumus O O.Flexural-torsional-coupled vibration analysis of axially loaded closed-section composite Timoshenko beam by using DTM [J].JournalofSoundandVibration,2007,306(3-5)：495-506.

[15] Kaya M O.Free vibration analysis of a rotating Timoshenko beam by differential transform method [J].AircraftEngineeringandAerospaceTechnology,2006,78(3):194-203.

[16] 滕兆春,王晓婕,付小华.弹性地基上变截面梁自由振动的DTM分析[J].兰州理工大学学报,2016,42(1):166-169.(TENG Zhao-chun，WANG Xiao -jie，FU Xiao-hua.Free vibration analysis of variable-area beams on elastic foundation by using DTM [J].JournalofLanzhouUniversityofTechnology,2016,42(1)：166-169.(in Chinese))

[17] Yalcin H S,Arikoglu A,Ozkol I.Free vibration ana-lysis of circular plates by differential transformation method [J].AppliedMathematicsandComputation,2009,212(2):377-386.

[18] Kumar Y.Free vibration analysis of isotropic rectangular plates on Winkler foundation using differential transform method [J].InternationalJournalofAppliedMechanicsandEngineering,2013,18(2):589-597.

[19] Kumar Y.Differential transform method to study free transverse vibration of monoclinic rectangular plates resting on Winkler foundation [J].AppliedandComputationalMechanics,2013,7(2):145-154.

[20] Lam K Y,Wang C M,He X Q.Canonical exact solutions for Levy-plates on two-parameter foundation using Green’s functions [J].EngineeringStructures,2000,22(4):364-378.

[21] Bhat R B,Laura P A A,Gutierrez R G,et al.Numerical experiments on the determination of natural frequencies of transverse vibrations of rectangular plates of non-uniform thickness [J].JournalofSoundandVibration,1990,138(2):205-219.