基于IGA-SIMP法的连续体结构应力约束拓扑优化
,
(大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116023)
1 引 言
拓扑优化是一种概念性的结构设计工具,通过确定设计域内孔洞的连通性、形状和位置,从而获得具有创新性的结构设计方案[1]。目前,随着制造技术的成熟,结构拓扑优化得到了快速的发展和广泛的应用,已经建立了各种不同的拓扑优化方法[2-6]。在工程结构设计中,需要考虑和关注应力水平的限制,以避免应力集中或高应力值所引起的结构断裂和疲劳破坏等现象。因此,应力相关的结构拓扑优化研究具有重要的实际意义和理论价值[7-10]。
最近,考虑应力约束的连续体结构拓扑优化问题受到了较多的关注[1]。一方面,单纯给定材料体积约束的柔顺度最小化设计已不能满足工程实际需要。另一方面,应力约束拓扑优化通常存在与应力约束函数相关的三个求解难题,即奇异最优解现象、应力约束的局部性质和应力行为的高度非线性。有关应力约束拓扑优化困难的论述以及解决方法的介绍参考文献[1,9]。
值得指出,应力约束拓扑优化问题的研究大多采用有限元分析方法(FEA)和密度法SIMP(Solid Isotropic Material with Penalization),基于双线性(Q4)有限单元密度变量的FEA-SIMP成为最常用的数值求解技术。然而,这种双线性单元并不能保证应力计算的精度,会影响优化结果的可信性。为了提高应力分析的精度,一些研究工作将扩展有限元方法和有限胞元法等与水平集优化方法相结合,有效地求解应力约束拓扑优化问题[10-12]。另一方面,等几何分析(IGA)作为一种新型的数值方法,为紧密地结合CAD和CAE开启了一条新途径[13,14]。相比于传统有限元方法,等几何分析具有几何精确性和基函数高阶连续性的特点,提高了结构分析的精度。而且,将等几何分析与结构优化设计结合,两者采用相同的NURBS函数,可提升结构分析与设计效率。
近年来,等几何分析方法已应用于拓扑优化问题的研究,通过与不同的拓扑优化方法结合,发展了各种等几何设计框架[15]。然而,除了文献[16]利用了等几何水平集方法以外,很少涉及应力约束的拓扑优化设计。为此,基于SIMP法简便且高效的特点,本文建立了一种IGA-SIMP框架下的连续体结构应力约束拓扑优化方法,实现了几何建模、结构分析和优化设计过程的集成。为有效地克服应力约束引起的拓扑优化困难,发展了一种基于稳定转换法修正的P-norm应力约束策略。给出了基于IGA-SIMP方法的两种应力约束拓扑优化列式,并采用梯度类优化算法——移动渐近线法MMA(Method of Moving Asymptotes)[17]更新设计变量。最后,通过几个典型平面应力问题的拓扑优化算例证明了本文方法的有效性和精确性。
2 结构等几何分析和设计参数化
等几何分析方法是基于等参思想,用表示几何模型的非均匀有理B样条(NURBS)基函数和控制点,代替有限元分析中的单元形函数和节点。具体而言,采用NURBS基函数对待求的物理场进行离散,如二维平面应力问题的位移函数可表示为
(1)

通常,等几何分析采用二次及以上的NURBS基函数(单元间至少具有C1连续性)。因此,高阶连续的等几何单元对于应力场的分析具有更高的计算精度。
其中,应力矩阵的计算表达式为
σ=DBu
(2)
式中B为应变位移矩阵,D为弹性矩阵。单元刚度矩阵为
(3)
此外,NURBS基函数用于描述拓扑优化设计密度法中材料的密度场,因此材料的密度分布可表示为
(4)
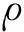
(5)

基于SIMP模型[3],单元的弹性矩阵计算表达式为
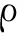
(6)
式中D0为实体材料的弹性矩阵,k取建议值3。
因此,由式(1,5),结构的几何建模、力学分析和设计参数化采用相同的NURBS函数,双线性和双二次NURBS单元分别对应N4和N9 IGA-SIMP。需要指出,双线性NURBS单元等价于传统的四节点拉格朗日单元。当采用更高阶次的NURBS单元时,相应地有N16和N25 IGA-SIMP。
3 IGA-SIMP法的应力约束拓扑优化列式
3.1 两种应力约束拓扑优化问题列式
本文考虑两种应力约束拓扑优化问题,即应力约束下的材料体积最小化设计以及体积和应力约束下的柔顺度最小化设计。相应的数学列式分别为
s. t.Ku=f

(7)
s. t.Ku=f
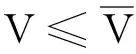

(8)
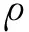
另外,对于具有中间相对密度的材料点的应力计算,需要定义另一种插值方案,其实质是为了克服奇异最优解的放松方法

(9)
式中Ba为应力计算点处的应变位移矩阵,s为应力惩罚系数,本文取文献[9]建议值s=0.5。因此,应力约束点a处的von Mises应力值为
(10)
式中 矩阵V的表达式为
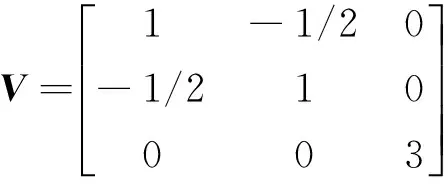
(11)
3.2 修正的P-norm应力约束
考虑应力约束的拓扑优化列式存在局部约束引起的较大计算量等问题。通常采用全局的 P-norm 或者Kreisselmeier-Steinhauser(K-S)凝聚函数来处理局部应力约束。然而,这两种近似的应力凝聚函数与最大应力之间具有一定的误差。针对这一问题,本文发展一种基于P-norm应力修正的约束方法,可以精确地实施最大应力约束,提高优化解的精度。同时,在精确应力修正的基础上引入稳定转换法(STM)的应力约束迭代格式,以避免迭代振荡和收敛困难。
基于P-norm的应力凝聚函数可表示为
(12)
式中p为凝聚参数。由式(12)可知
(13)
因此,采用应力函数表达式(12)施加最大应力约束会产生一定的误差,不利于保证解的精度,对于小的p值尤其如此。同时,这种误差可能使得优化算法找不到合适的解。另一方面,随着p值的增大,应力函数的近似误差会减小。然而,较大的p值将引起约束函数的高度非线性,产生迭代振荡问题和数值计算困难。
基于此,与文献[9]类似,利用一种修正的P -norm应力函数约束方法,即
(14)
式中cp为应力修正参数。在优化迭代步n≥1时,
(15)
因此,优化问题列式(7,8)的约束函数可表示为
(16)
值得指出的是,在优化迭代过程中,cp是一个变化的值。某些情况下,这种不连续的应力修正方法会引起迭代振荡和收敛困难。
针对迭代计算不稳定问题,本文发展一种基于稳定转换法的应力修正列式。原来用于解决迭代算法数值失稳和实现收敛控制的稳定转换法[18]可表达为
xk +1=xk+qC[g(xk)-xk]
(17)
式中 0 xk +1=xk+q[g(xk)-xk] (18) 将其拓展应用于应力修正式(15),可得到基于稳定转换法的应力修正参数: (19) 当q=1时,式(19)退化为式(15),即实施精确的P-norm应力修正。而当优化过程中发生迭代振荡引起收敛困难时,采用式(19),且0 本文发展的应力修正策略与文献[9,19]的P-norm 应力度量的不同,后者的应力规格化系数用前面迭代步的信息来近似最大应力。比较而言,本文的约束策略是基于精确的应力修正思想,与稳定转换法结合,以抑制优化迭代振荡和收敛困难。此外,建立了IGA-SIMP框架下的伴随灵敏度分析列式,设计变量为NURBS控制点所对应的密度变量。 考虑经典的L形梁体积最小化设计,即优化问题(7)。设计域和边界条件如图1所示,结构分析采用单片NURBS剪裁等几何分析方法。为了与文献[19]的Q4 FEA-SIMP优化结果进行对比,本节采用N4 IGA-SIMP结合P-norm应力修正约束策略。结构的设计域由6400个双线性单元离散,正方形单元的边长为1 mm。外荷载F=500 N分配到相邻的5个单元上。 图2和图3分别展示了凝聚参数p取6和8时的优化结果,其中应力约束采用修正式(15),即式(19)中令q=1。可以看出,这两个优化结果均可以避免高度的应力集中,p=8时的材料用量更少。然而,图4所示的迭代历史表明,p=6时的迭代曲线具有更好的收敛性,135步可以满足收敛准则。而p=8时的迭代过程存在振荡现象,且不能自动满足本文的收敛准则,优化结果由最大迭代数决定。并且,这种振荡行为对于其他的最大迭代数情况可能得不到满足要求的设计。 图1 L形梁的设计域和边界条件 Fig.1 Design domain and boundary condition of L-shaped beam 图2 L形梁的优化结果 (p=6,q=1,V/V0=27.4%,σmax=357.9 MPa) Fig.2 Optimized results of L-shaped beam (p=6,q=1,V/V0=27.4%,σmax=357.9 MPa) 图3 L形梁的优化结果 (p=8,q=1,V/V0=26.1%,σmax=357.8 MPa) Fig.3 Optimized results of L-shaped beam (p=8,q=1,V/V0=26.1%,σmax=357.8 MPa) 图4 材料体积和最大应力的迭代历史 Fig.4 Iterative histories of material volume and maximum stress 图5 L形梁的优化结果 (p=8,q=0.5,V/V0=26.5%,σmax=357.8 MPa) Fig.5 Optimized results of L-shaped beam (p=8,q=0.5,V/V0=26.5%,σmax=357.8 MPa) 图6 L形梁的优化结果 (p=8,q=0.1,V/V0=26.3%,σmax=357.2 MPa) Fig.6 Optimized results of L-shaped beam (p=8,q=0.1,V/V0=26.3%,σmax=357.2 MPa) 图7 材料体积和最大应力的迭代历史 Fig.7 Iterative histories of material volume and maximum stress 因此,应采用基于稳定转换法的应力修正式(19),且0 考虑图1所示L形梁的柔顺度最小设计问题。体积限制不小于4.1节的体积最小化结果。算例同时采用N4和N9 IGA-SIMP,单元的细分水平及荷载的分配方式同4.1节。需要指出,结构分析中采用不同的单元类型对计算的应力水平会有影响。如本文用N4和N9两种单元对图1所示L形梁初始分析的最大应力分别为388.5 MPa和481.9 MPa。相比于双线性的N4单元,N9单元的应力计算精度更高。 图9和图10分别为N4和N9 IGA-SIMP方法的柔顺度最小化结果,采用的应力修正式(19)的参数q=1,凝聚参数p值分别设为8和12。由于初始最大应力水平的不同,图9和图10的体积约束分别设为V≤2000 mm3和V≤2300 mm3。可以看出,本文方法可以获得满足应力约束要求的设计。相比N4 IGA-SIMP,N9 IGA-SIMP方法可以提高应力及其灵敏度的计算精度,加强优化结果的可信性。另外,图11分别展示了相应的迭代历史。相比体积最小化设计的迭代历史(图4(b)),图11呈现了更加稳定的迭代过程和较好的收敛性。因此,无稳定转换法控制的P-norm应力修正策略适合于求解最小柔顺度的拓扑优化问题(8)。 图8 FEA-SIMP方法的优化结果[19] (V/V0=29.3%,σmax=357.7 MPa) Fig.8 Optimized result of FEA-SIMP method (V/V0=29.3%,σmax=357.7 MPa) 图9 L形梁的优化结果 (p=8,q=1,σmax=357.5 MPa) Fig.9 Optimized results of L-shaped beam (p=8,q=1,σmax=357.5 MPa) 与4.1节优化结果对比,两种优化列式的L形梁设计均可以通过改进图1的90°拐角处的材料分布,实现消除应力集中的作用。然而,由于优化问题列式的不同,所得到的拓扑构型和应力分布(其中图6的σmax=357.2 MPa,图9的σmax=357.5 MPa)存在差异。体积最小化设计可以充分利用材料,其优化结果的不同区域应力水平更加接近,即更加趋近于满应力的设计。而柔顺度最小化设计在满足应力和体积限制的条件下,更关心目标柔顺度的降低,可以得到兼顾结构的刚度和强度性能的优化解。 图10 L形梁的优化结果 (p=12,q=1,σmax=357.9 MPa) Fig.10 Optimized results of L-shaped beam (p=12,q=1,σmax=357.9 MPa) 图11 平均柔顺度和最大应力的迭代历史 Fig.11 Iterative histories of mean compliance and maximum stress 考虑1/4圆环结构的应力约束拓扑优化设计,如图12所示。采用N9 IGA-SIMP,同时考虑优化问题(7,8)。其中,NURBS单元的细分水平为120×80,集中载荷F=2000 N施加到相邻的10个单元上,凝聚参数p=10。 根据4.1节的算例讨论,基于稳定转换法的应力修正策略适合于求解优化问题(7)。因此,将式(19)的q取为0.1,可以得到应力约束的体积最小化设计解,如图13所示。然后,根据优化结果中的材料体积比,采用本文方法求解优化问题(8)。其中,体积限制为V≤11000 mm3,相应的优化结果如图14所示。结果表明,IGA-SIMP方法可以获得满足约束要求的最优拓扑设计。图13优化解的高应力区域分布得更加均匀,而图14是同时考虑结构刚度和强度性能的设计方案。 图12 1/4圆环结构的设计域和边界条件 Fig.12 Design domain and boundary condition of the quarter annulus structure 图13 体积最小化设计结果 (p=10,q=0.1,V/V0=41.7%,σmax=357.3 MPa) Fig.13 Optimized results of volume minimization design (p=10,q=0.1,V/V0=41.7%,σmax=357.3 MPa) 提取图14中柔顺度最小化拓扑优化结果的结构边界,然后在Abaqus通用软件中建模并分析(单元类型为CPS4),两种有限元网格尺寸的应力分析结果如图15所示。可以看出,随着网格的加密,结构右下端固定处的最大应力值由335.5 MPa增加至352.8 MPa;而图14中该区域的最大应力值为356.9 MPa。因此,本文等几何应力分析与加密后的有限元应力分析结果接近,表明等几何分析的应力计算是准确的。理论上,由于等几何分析的精确几何建模和单元之间高阶连续的优点,其比有限元框架具有更高的应力计算精度。图16展现了平稳的优化迭代过程,表明基于稳定转换法修正的约束方法可以克服应力约束的求解困难和迭代振荡,获得高精度的优化解。 图14 柔顺度最小化设计结果 (p=10,q=1,σmax=356.9 MPa) Fig.14 Optimized results of compliance minimization design (p=10,q=1,σmax=356.9 MPa) 图15 图14优化结果的有限元分析应力分布 Fig.15 Stress distribution of FEA for optimized results in Fig.14 图16 圆环结构的优化迭代历史 Fig.16 Iterative histories of topology optimization of the annulus structure 本文建立了连续体结构应力约束拓扑优化的IGA-SIMP方法,实现了几何建模、结构分析和优化设计过程的紧密结合。为了处理局部应力约束,同时保证凝聚函数的近似精度,提出了基于稳定转换法修正的P-norm应力约束策略。典型的平面应力问题拓扑优化算例证明了本文方法的有效性和精确性,主要结论如下。 (1) 相比于传统的FEA-SIMP方法,IGA-SIMP促进了结构分析与优化设计的集成统一,且结合P-norm应力修正策略的拓扑优化解的质量更高。 (2) 由于几何精确性和单元之间高阶连续性的优点,等几何分析可提高应力及其灵敏度的计算精度,从而加强了拓扑优化结果的可信性。 (3) 对于体积最小化问题,稳定转换法修正的应力约束策略可以抑制迭代振荡,获得稳定收敛的优化解;而对于柔顺度最小化问题,其迭代过程相对稳健,采用精确修正的应力约束策略即可获得满足约束条件的拓扑优化方案。 (4) 体积最小化列式可实现趋近于满应力的拓扑优化设计,而柔顺度最小化列式可获得兼顾结构刚度和强度性能的设计方案。 参考文献(References): [1] Deaton J D,Grandhi R V.A survey of structural and multidisciplinary continuum topology optimization:post 2000[J].StructuralandMultidisciplinaryOptimization,2014,49(1):1-38. [2] Sigmund O,Maute K.Topology optimization approaches [J].StructuralandMultidisciplinaryOptimization,2013,48(6):1031-1055. [3] Bendsoe M P,Sigmund O.TopologyOptimization:Theory,Methods,andApplications[M].Berlin:Sprin-ger Science & Business Media,2003. [4] 王 选,祝雪峰,胡 平,等.基于NURBS插值的三维渐进结构优化方法[J].计算力学学报,2016,33(4):536-542.(WANG Xuan,ZHU Xue -feng,HU Ping,et al.Bi-directional evolutionary method using NURBS interpolation for optimal design of 3D continuum structures [J].ChineseJournalofComputationalMechanics, 2016,33(4):536-542(in Chinese)) [5] 仝立勇,骆泉添.用拓扑优化设计多体分比蜂窝状结构 [J].计算力学学报,2016,33(4):516-521.(TONG Li-yong,LUO Quan-tian.Design of cellular structures with multi-volume fractions using topology optimization [J].ChineseJournalofComputationalMechanics,2016,33(4):516-521.(in Chinese)) [6] 周海涛,张大可,杨毅超,等.基于虚拟材料的T-B梁拓扑优化ESO方法 [J].计算力学学报,2017,34(2):143-147.(ZHOU Hai-tao,ZHANG Da-ke,YANG Yi-chao,et al.Study of ESO on Tie-beam problem using virtual material [J].ChineseJournalofComputationalMechanics,2017,34(2):143-147.(in Chinese)) [7] 隋允康,叶红玲,彭细荣.应力约束全局化策略下的连续体结构拓扑优化 [J].力学学报,2006,38(3):364-370.(SUI Yun-kang,YE Hong-ling,PENG Xi-rong.Topological optimization of continuum structure under the strategy of globalization of stress constraints [J].ChineseJournalofTheoreticalandAppliedMechanics,2006,38(3):364-370.(in Chinese)) [8] 荣见华,葛 森,邓 果,等.基于位移和应力灵敏度的结构拓扑优化设计 [J].力学学报,2009,41(4):518-529.(RONG Jian-hua,GE Sen,DENG Guo,et al.Structural topological optimization based on displacement and stress sensitivity analysis [J].ChineseJournalofTheoreticalandAppliedMechanics,2009,41(4):518-529.(in Chinese)) [9] Le C,Norato J,Bruns T,et al.Stress-based topology optimization for continua [J].StructuralandMultidisciplinaryOptimization,2010,41(4):605-620. [10] Guo X,Zhang W S,Wang M Y,et al.Stress-related topology optimization via level set approach [J].ComputerMethodsinAppliedMechanicsandEngineering,2011,200(47-48):3439-3452. [11] Wang M Y,Li L.Shape equilibrium constraint:a strategy for stress-constrained structural topology optimization [J].StructuralandMultidisciplinaryOptimization,2013,47(3):335-352. [12] Cai S Y,Zhang W H,Zhu J H,et al.Stress constrained shape and topology optimization with fixed mesh:a B-spline finite cell method combined with level set function [J].ComputerMethodsinAppliedMecha-nicsandEngineering,2014,278:361-387. [13] Hughes T J R,Cottrell J A,Bazilevs Y.Isogeometric analysis:CAD,finite elements,NURBS,exact geometry and mesh refinement [J].ComputerMethodsinAppliedMechanicsandEngineering,2005,194(39):4135-4195. [14] Cottrell J A,Hughes T J R,Bazilevs Y.IsogeometricAnalysis:TowardIntegrationofCADandFEA[M].New York:John Wiley & Sons,2009. [15] Nguyen V P,Anitescu C,Bordas S P A,et al.Isogeometric analysis:an overview and computer implementation aspects [J].MathematicsandComputersinSimulation,2015,117:89-116. [16] Jahangiry H A,Tavakkoli S M.An isogeometrical approach to structural level set topology optimization [J].ComputerMethodsinAppliedMechanicsandEngineering,2017,319:240-257. [17] Svanberg K.The method of moving asymptotes—a new method for structural optimization [J].InternationalJournalforNumericalMethodsinEngine-ering,1987,24(2):359-373. [18] Yang D X,Yang P X.Numerical instabilities and convergence control for convex approximation methods [J].NonlinearDynamics,2010,61(4):605-622. [19] Jeong S H,Yoon G H,Takezawa A,et al.Development of a novel phase-field method for local stress-based shape and topology optimization [J].Compu-ters&Structures,2014,132:84-98.4 应力约束下结构拓扑优化算例
4.1 L形梁的体积最小化设计








4.2 L形梁的柔顺度最小化设计
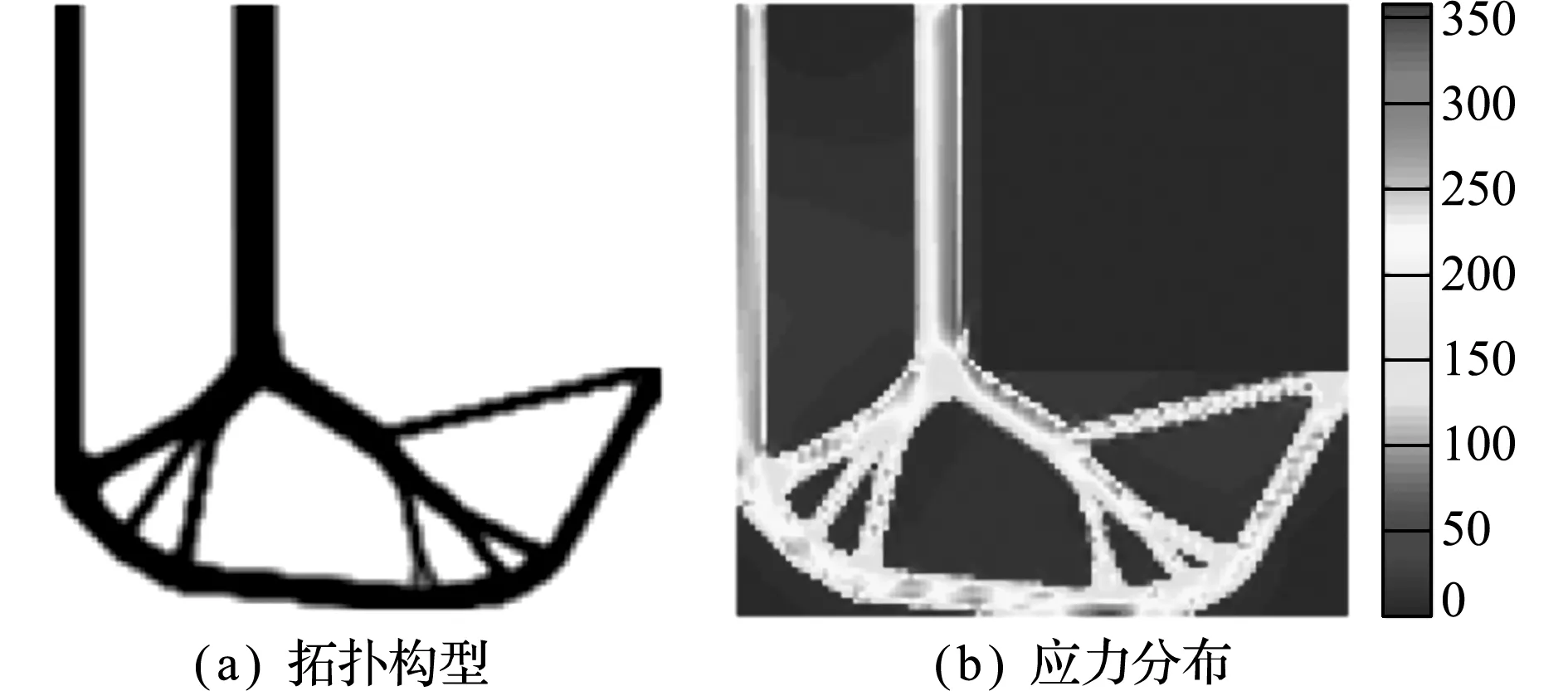
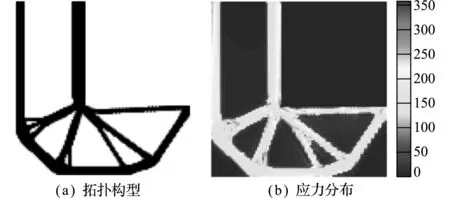

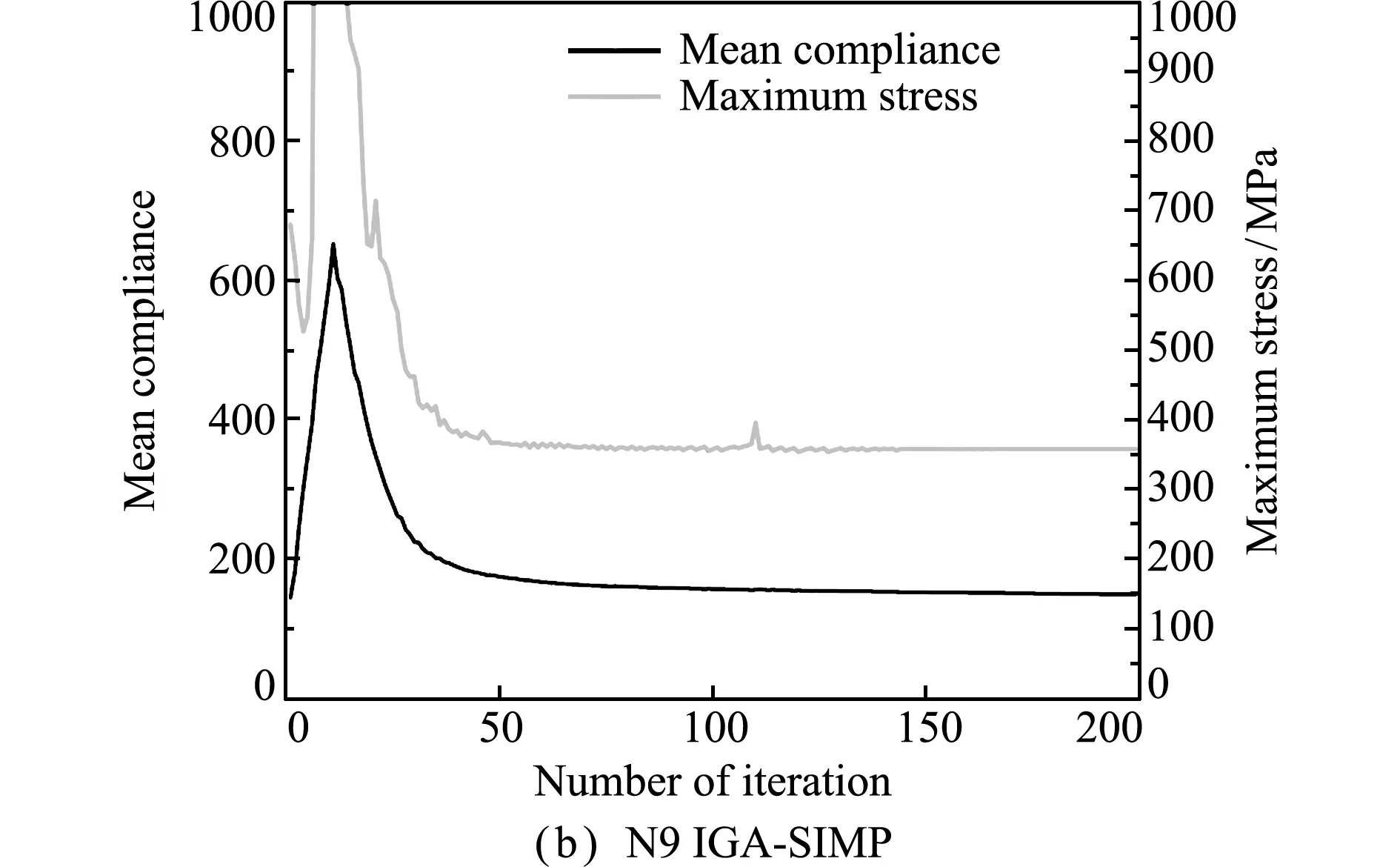
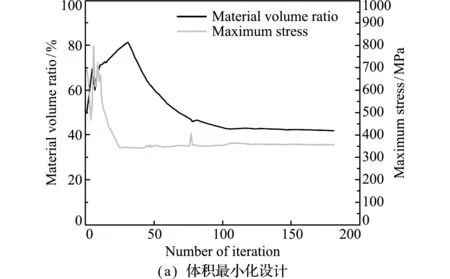
4.3 1/4圆环结构的拓扑优化设计
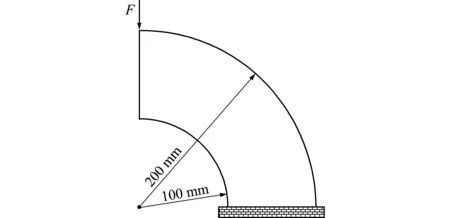





5 结 论

