气体吸附方程和解吸方程的推导及应用

陈元千 傅礼兵 郝明强

(中国石油勘探开发研究院 北京 100083)

非常规的页岩吸附气和煤层吸附气是国家资源的重要组成部分，在我国拥有丰富的资源潜力和开发利用前景，仅在2016年页岩气和煤层气的产量已超过120亿m3，约占全国天然气总产量的10%。在对页岩吸附气和煤层吸附气的资源评价和开发利用评价时，累积吸附量方程和吸附量方程具有重要的地位,因而引起了国内外专家学者的高度重视，并开展了多年的室内实验研究工作，取得了大量的吸附实验数据，发表了许多相关的论文,但所使用的基础理论方法均为Langmuir(兰格苗尔)的吸附方程[1]。本文基于页岩气和煤层气的大量吸附实验数据，利用油气藏工程的原理和方法，推导得到了页岩气和煤层气的累积吸附量方程和吸附量方程，以及累积解吸量方程和解吸量方程。同时，基于Langmuir的累积吸附量经验方程，推导得到了兰氏的吸附量方程、累积解吸量方程和解吸量方程。

1 吸附量方程和解吸量方程的推导

1.1 吸附量方程的推导

图1是康永尚 等[2]根据煤层气的等温吸附实验数据绘成的等温累积吸附量曲线。由图1看出，在初期累积吸附量随压力快速增加，而后逐步变缓，最后趋近一个饱和累积吸附量。本文基于Arps[3]的产量随时间下降的递减率概念，提出了页岩吸附气量或煤层吸附气量随吸附压力变化的递减率为

(1)

图1 煤层气等温吸附实验累积吸附量与吸附压力关系图[2]

若吸附量随吸附压力变化的递减率B为常数时，对式(1)分离变量，并代入积分上下限得

(2)

由式(2)的积分得气体的吸附量方程为

q=qsce-B(p-psc)

(3)

累积吸附量表示为

(4)

将式(3)代入式(4)积分后,得气体的累积吸附量方程为

-e-B(p-psc)]

(5)

由于式(5)中的qsc和B都是常数，可用下面的一个新的常数表示为

A=qsc/B

(6)

将式(6)代入式(5),得本文的等温累积吸附量方程为

v=A[1-e-B(p-psc)]

(7)

将式(7)对压力求导,可得吸附量方程为

q=ABe-B(p-psc)

(8)

由式(3)和式(8)对比看出，qsc=AB，因此，qsc是一个不需要测定的重要物理量。根据累积吸附量实验数据，为了确定式(7)中常数A和B的数值，先将式(7)改写为下式：

(9)

再将式(9)等号两端取自然对数,可得如下的直线关系式：

-psc)

(10)

由式(10)看出，这是一个半对数的直线关系。当给定不同的A值，由式(10)进行线性迭代试差得到的最佳直线(相关系数最大)的A值，就是要求的正确A值。最后，再由式(10)的线性回归确定B的数值。

1.2 解吸量方程的推导

当压力从饱和吸附压力ps，即初始解吸压力降到压力p时，累积解吸量表示为

v*=vs-v

(11)

由式(7)可写出饱和累积吸附量为

vs=A[1-e-B(ps-psc)]

(12)

将式(7)和式(12)代入式(11)得，当压力从ps降到p时的累积解吸量为

v*=A[e-B(p-psc)-e-B(ps-psc)]

(13)

式(13)对压力求导,得解吸量方程为

q*=ABe-B(p-psc)

(14)

由式(8)和式(14)对比看出，吸附量方程和解吸量方程是相同的，也可以说两者是可逆的。

2 兰氏累积吸附量经验方程及有关推导

2.1 兰氏的累积吸附量经验方程

美国的物理和化学家Langmuir(兰格苗尔)根据室内大量气体累积吸附量实验数据的变化分析，于1918年提出了著名的兰氏累积吸附量经验方程,这是当今评价页岩气和煤层气资源和开发利用时的重要基础。图2是利用兰氏的实验数据[1]绘成的CH4、N2和CO2在90 K下的累积吸附量曲线。

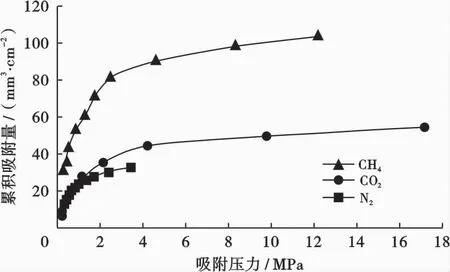
图2 兰氏的累积吸附量和吸附压力的实验数据曲线

兰氏提出，累积吸附量随压力的变化，开始呈近乎直线的增加，而后变得缓慢，最后趋于一个饱和值。正基于此，兰氏直接提出了如下的累积吸附量经验方程[1]：

(15)

式(15)中的a和b是2个与吸附气的物理性质和温度等因素有关的常数。

将式(15)对压力求导,得兰氏的吸附量方程为

(16)

根据实验测试数据，为了确定兰氏经验方程中常数a和b的数值，将式(15)改为如下的直线关系式[4-6]：

(17)

由式(17)看出，a是直线的截距，-b是直线斜率的倒数。

Ahamed等[4]提出的兰氏体积常数和兰氏压力常数分别表示为vL=a和pL=1/b，由式(15)可得我国许多文献[2,5-15]所引用的兰氏累积吸附量经验方程为

(18)

将式(18)对压力求导,得Ahamed的兰氏吸附量经验方程为

(19)

2.2 兰氏累积解吸量方程和解吸量方程的推导

在饱和吸附压力ps下兰氏的饱和累积吸附量，由式(15)可写为

(20)

当压力由ps降到压力p时的累积解吸量表示为v*=vs-v，即式(11)。

将式(15)和式(20)代入式(11),得兰氏的累积解吸量方程为

(21)

将式(21)对压力求导,得兰氏的解吸量方程为

(22)

3 实例应用与对比

表1列出了美国San Juan盆地煤样吸附测试取得的累积吸附量与吸附压力数据[4]。

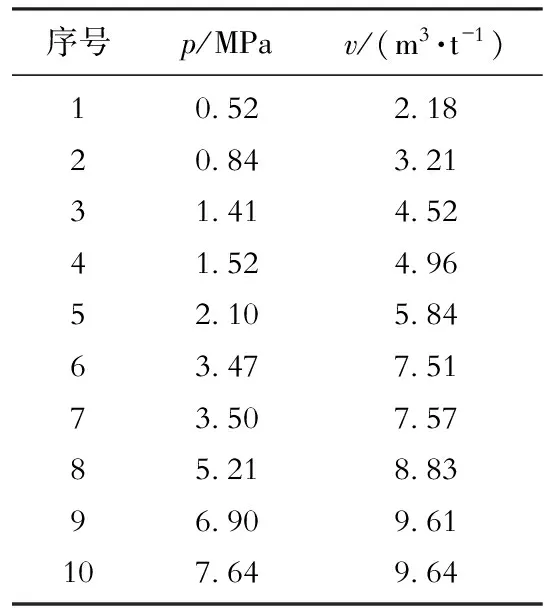
表1 San Juan 盆地煤样的吸附气测试数据[4]

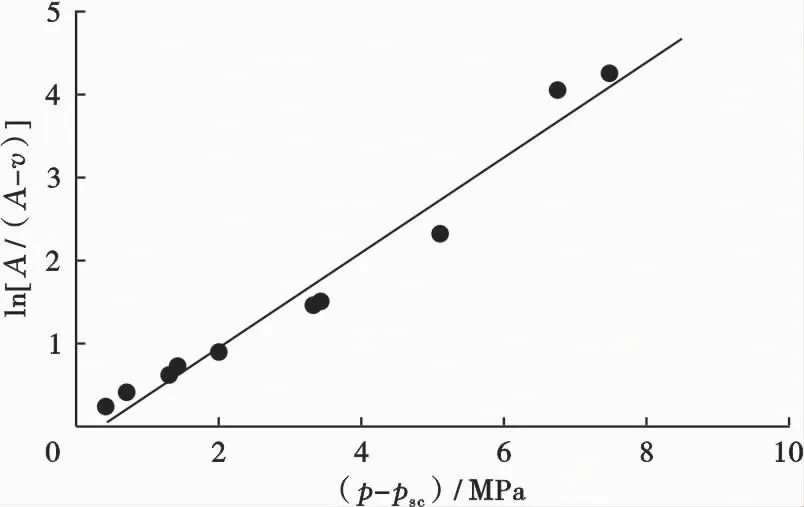
图3 式(10)的最佳直线关系图

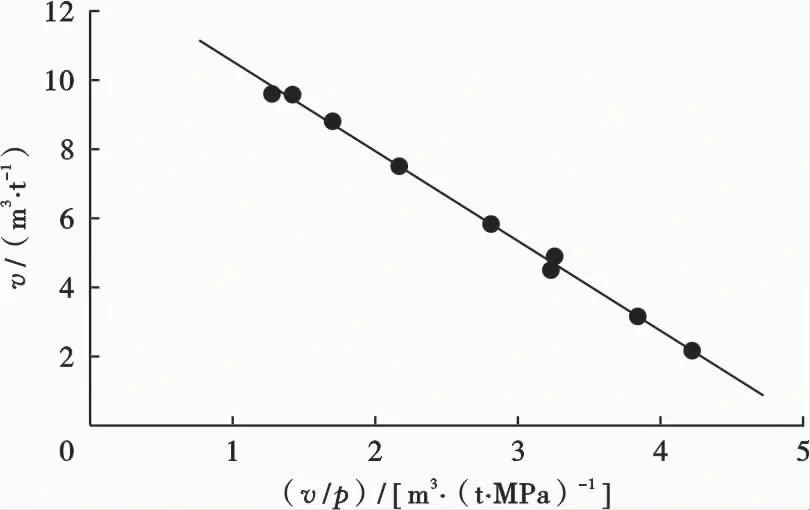
图4 式(17)的最佳直线关系图

利用表1中的数据，根据式(10)和式(17)，分别绘成的线性关系图见图3和图4，由图3线性回归求得本文方法的A为9.778 m3/t、B为0.473 8 MPa，线性相关系数为0.9983。由图4线性回归求得兰氏方法的a为12.61 m3/t、b为0.446 4 MPa，线性相关系数为0.999 3。

将A和B的值分别代入式(7)、(8)，可得本文方法预测累积吸附量和吸附量的关系式为

v=9.778[1-e-0.473 8(p-psc)]

(23)

q=4.633e-0.473 8(p-psc)

(24)

同样，将a和b的值分别代入式(15)、(16)，可得兰氏法预测累积吸附量和吸附量的关系式为

(25)

(26)

将由式(23)、(24)预测的结果以及由式(25)、(26)预测的结果绘于图5。由图5看出，本文方程与兰氏经验方程预测的结果基本一致,这对2种方程的正确性也起到了相互佐证的作用。

将A和B的值分别代入式(13)、(14)，可得本文方法预测累积解吸量和解吸量的关系式为

v*=9.778[e-0.473 8(p-psc)-e-0.473 8(ps-psc)]

(27)

q*=4.633e-0.473 8(p-psc)

(28)

图5 2种方法的预测值与实测值对比

将a和b的值分别代入式(21)、(22)，可得兰氏法预测累积解吸量和解吸量的关系式为

(29)

(30)

若设ps=10 MPa，并知psc=0.101 MPa，由本文的式(27)、(28)以及由兰氏方法的式(29)、(30)分别预测的累积解吸量和解吸量绘于图6。由图6看出，兰氏方法预测的结果偏高。

图6 2种方法等温累积解吸量和解吸量的预测结果对比

4 结论

基于室内大量的吸附气实验数据，应用油气藏工程的原理和方法，提出了气体吸附量随吸附压力的递减率的定义，经推导得到了页岩气和煤层气的累积吸附量方程和吸附量方程，以及累积解吸量方程和解吸量方程。同时，在研究兰氏的累积吸附量经验方程的基础上，经推导得到了兰氏的吸附量方程、累积解吸量方程和解吸量方程。实例应用表明，本文方程和兰氏方程预测结果基本一致，但兰氏的偏高，两者可以起到相互佐证的作用。

应当指出，Ahamed变换的兰氏累积吸附量经验方程在我国许多文献应用时,采用经验取值法确定兰氏体积常数vL和兰氏压力常数pL的数值是不正确的,该方法是将实例的最大累积吸附量vmax作为vL值，再将vmax/2所对应的压力作为pL值。确定vL和pL的正确方法应当是采用本文的式(17)。

符号注释

v—等温累积吸附量，m3/t；

vs—饱和累积吸附量，m3/t；

vL—兰氏体积常数；

v*—等温累积解吸量，m3/t；

q—等温吸附量，m3/(t·MPa)；

q*—等温解吸量，m3/(t·MPa)；

qsc—等温吸附条件psc压力下的吸附量，m3/(t·MPa)；

p—吸附压力或解吸压力，MPa；

ps—饱和吸附压力，MPa；

pL—兰氏压力常数；

psc—地面标准条件压力(0.101 MPa)，MPa；

R—相关系数；

A和B—本文吸附量方程常数；

a和b—兰氏吸附量经验方程常数。

[1] LANGMUIR I.The adsorption of gases on plane surfaces of glass,mica and platinum[J].J.Am.Chem.Soc.,1918:1361-1402.

[2] 康永尚，王金，姜杉钰，等.量化指标在煤层气开发潜力定量评价中的应用[J].石油学报，2017，38(6)：677-686.

KANG Yongshang，WANG Jin,JIANG Shanyu,et al.Application of quantitative indexes in quantitative evaluation of coalbed methane development potential[J].Acta Petrolei Sinica,2017,38(6):677-686.

[3] ARPS J J.Analysis of decline curves[J].Trans.AIME,1945,160:228-247.

[4] AHAMED T H，MCKINNEY P D.Advanced reservoir engineering[M].Gulf Publishing Company,Houston,Texas,2004,3:217-232.

[5] 陈元千，郭二鹏，齐亚东.关于确定兰氏体积和兰氏压力的方法[J].断块油气田，2015，22(1):67-69.

CHEN Yuanqian,GUO Erpeng,QI Yadong.A method for determining Langmuir’s volume and Langmuir’s pressure[J].Fault-Block Oil & Gas Field,2015,22(1):67-69.

[6] 陈元千，胡建国.确定饱和型煤层气藏地质储量、可采储量和采收率方法的推导及应用[J].石油与天然气地质，2008，29(1)：151-156.

CHEN Yuanqian,HU Jianguo.Derivation of methods for estimating OGIP and recoverable reserves and recovery ratio of saturated coal-seam gas reservoirs[J].Oil & Gas Geology,2008,29(1):151-156.

[7] 陈元千，李剑，齐亚东，等.页岩气藏地质资源量、可采资源量和井控可采储量的确定方法[J].新疆石油地质，2014，35(5):547-551.

CHEN Yuanqian,LI Jian,QI Yadong,et al.Determination methods of geological resources,recoverable resources and well controlled recoverable reserves in shale gas reservoir[J].Xinjiang Petroleum Geology,2014,35(5):547-551.

[8] 熊伟，郭为，刘洪林.页岩的储层特征以及等温吸附特征[J].天然气工业，2012，32(1)：113-116.

XIONG Wei,GUO Wei,LIU Honglin.Shale reservoir characteristics and isothermal adsorption properties[J].Natural Gas Industry,2012,32(1):113-116.

[9] 武瑾，王红岩，拜文华,等.渝东南龙马溪组页岩储层特征及吸附影响因素分析[J].断块油气田，2013，20(6)：713-718.

WU Jin,WANG Hongyan,BAI Wenhua,et al.Analysis on characteristics of Longmaxi Formation shale reservoir in southeast district of Chongqing and adsorption influence factor[J].Fault-Block Oil & Gas Field,2013,20(6):713-718.

[10] 倪小明，苏现波，张小东.煤层气开发地质学[M].北京：化学工业出版社，2010：126-128.

[11] 张卫东，王瑞和.煤层气开发概论[M].北京：石油工业出版社，2013：45-46.

[12] 张新民，庄军，张遂安.中国煤层气地质与资源评价[M].北京：科学出版社，2002：33-35.

[13] 中国煤田地质总局.中国煤层气资源[M].北京：中国矿业大学出版社，1999：101-102.

[14] 苏现波，陈江峰，孙俊民.煤层气地质学与勘探开发[M].北京：科学出版社，2001：47-49.

[15] 李武广，杨胜来，徐晶.考虑地层温度和压力的页岩吸附气含量计算新模型[J].天然气地球科学，2012，23(4)：791-796.

LI Wuguang,YANG Shenglai,XU Jing.A new model for shale adsorptive gas amount under a certain geological conditions of temperature and pressure[J].Natural Gas Geoscience,2012,23(4):791-796.