基于信息熵和Lempel-Ziv的生产线复杂性测度与线平衡
范国良, 李爱平, 刘雪梅, 徐立云
(同济大学 机械与能源工程学院,上海 201804)
随着制造系统复杂程度的不断加深,制造环境中大量不确定因素增加了生产线规划和决策的难度[1].操作人员疲劳、设备维护不及时,零部件缺陷等会引起作业时间波动,并影响生产线平衡方案执行的有效性[2].因此,必须对系统运行过程中的不确定因素进行定量化评价,对生产线平衡方案进行多目标优化,提高制造系统应对内外部环境动态变化的鲁棒性.
生产线平衡是一种实现劳动生产率、设备利用率和满足市场需求三者间平衡的过程[3].在实际生产过程中,以作业时间确定为假设得到的平衡方案会受诸多不确定因素的干扰,作业时间出现波动,导致制造系统难以维持稳定有序的生产过程.国内外学者针对此问题进行了一系列研究.目前,主要的研究方法有概率论方法(正态分布为代表)、复杂性方法(信息熵为代表)、基于仿真的方法等.Saif等[2],Dong等[4],Özcan等[5],Nazarian等[6]都针对作业时间波动的随机型装配线,假设实际作业时间服从正态分布,以分布函数的相关参数描述作业时间受不确定因素的影响程度,得到的平衡方案具有较高的鲁棒性.另外,诸多学者在概率论方法的基础上,将生产成本、物流稳定性和生产效率等过程指标作为优化目标或约束,以降低不确定因素对系统运行过程的影响.Cakir等考虑作业时间波动因素,建立了以最小平滑指数和最小化设计成本为目标的优化模型[7].刘俨后等提出描述工位在给定完工率下最小投产间隔的完工率节拍的概念,并建立装配线平衡模型[8].唐秋华等为减少因操作工时波动引起的生产效率损失或生产秩序中断,提出基于物流运输特性的U型装配优先关系约束条件,以保证入口和出口线上的物流顺行[9].复杂性理论作为测度不确定性的有效方法,被广泛应用于衡量制造系统设计、规划和运行过程中的多种不确定因素[10].Efthymiou等应用Lempel-Ziv方法度量制造过程中的不可预测性因素,通过分析产出量的波动测度制造系统的复杂度[11].何非、饶运清等提出了装配关系复杂性的度量方法,并应用到装配线动态平衡中,以最小装配关系复杂性差异度为优化目标,降低了各工作站的错误发生率和总完工时间[12].
综上所述,现有针对作业时间不确定的生产线平衡研究在一定程度上降低了作业时间不确定对平衡方案的影响.但是,仍存在以下问题需要深入研究:①将作业时间波动假设为服从正态分布具有一定的局限.不同类型工位服从的分布不同,所以,这一类方法的通用性仍需完善.②制造系统的复杂性研究缺乏作业时间不确定性的度量方法.从操作和工位状态角度定量评价不确定因素对作业时间波动的影响程度,才能建立生产工艺与平衡方案有效性之间的联系,进而指导随机型生产线的优化.
本文基于信息熵提出作业元素、工作站复杂性测度方法,基于Lempel-Ziv算法测度整线复杂度.进而建立以平衡率最高、复杂度均衡指数最小和整线复杂度最小的平衡优化模型.平衡生产线节拍保证效率的前提下,均衡各工作站复杂度来控制作业时间波动在系统内部的影响范围.同时,通过降低系统整线复杂度,减少不确定因素对生产线生产流程的影响,最终达到优化系统运行的目的.
1 考虑复杂性的生产线平衡模型
1.1 作业时间波动的不确定因素分析
生产线平衡是指对给定的传输速度和作业总量,如何尽可能均衡地将装配作业分配给沿线各工作站,而又不违反各作业元素执行先后顺序的限制,并保证各工作站的总作业时间不超过规定的周期[13].即以各工作站的工作时间为出发点进行研究,目的是最大化生产线的生产效率[14],所以平衡率高是生产线平衡优化首先要保证的前提.
然而,实际的生产环境中,生产操作会受产品缺陷、设备故障和人员疲劳等不确定因素的影响,继而出现操作失误及作业时间波动等问题.如果同一工作站出现失误的几率偏大,将引起后续工作站操作延迟的连锁反应.复杂度高的工作站作业时间波动程度更高,若干复杂的作业元素分配到同一工作站时,尽管节拍平衡,但该工作站负荷仍然很重.那么,需要从操作失误率出发,量化作业元素复杂度和工作站复杂度,进一步以工作站复杂度均衡为指标建立优化目标,以避免因复杂度累积出现瓶颈工作站.
另外,工作站状态的波动将影响生产过程的稳定性,直接关系到产品生产过程中的偏差累积.需要从系统角度定量评价工作站状态差异对整线运行状态的影响程度,进一步优化和控制系统整线复杂度,才能够降低工作站常见突发事件和生产扰动对正常生产流程的影响.
因此,生产线平衡优化模型需同时考虑以下3个优化目标:①平衡率最高,保证生产效率;②复杂度均衡指数最小,降低各工作站操作的复杂度差异;③整线复杂度最小,控制工作站状态波动对整线运行状态的影响,确保生产线整体生产过程的稳定有序.综上分析,可按图1所示流程建立生产线平衡优化模型,求解平衡率最高,各工作站复杂度最均衡和整线复杂度最低的作业元素最优划分方案.

图1 复杂性测度及生产线平衡流程图Fig.1 Complexity measurement and balancingflow chart of production line
1.2 基于信息熵的过程复杂性测度
确定系统复杂程度的通用测度是难以实现的,不同复杂性特征影响系统复杂度的机制不同,所以对于确定的问题要给出具有针对性的测度方法.目前,复杂性测度主要利用信息论及熵度量等方法对制造系统中的复杂性特征进行分解和定量化分析.信息论认为信息的概念与概率是紧密联系的,概率小的事件提供的信息比概率较大事件发生时提供的信息价值要大.将这一概念定量化也可以表述为信息消除的不确定性越大,所包含的信息量也越大[15].在生产过程中,操作失误等小概率的不确定因素包含的信息量比正常生产过程包含的信息量大,将增大工作站复杂度和整线复杂度.基于此可以通过测得各作业元素的状态及失误率,定义作业元素复杂度,并进一步定义工作站复杂度,来定量化评价各工作站的复杂程度,为生产线平衡实现各工位复杂度均衡化奠定基础.
测得各作业元素的失误率P(xi),根据信息熵定义作业元素复杂度hi为
hi=-P(xi)logrP(xi)
(1)
工作站复杂度的表达式为
(2)
式中:i为作业元素编号;hi为第i个作业元素的复杂度;P(xi)为第i个作业元素的失误率;xi为第i个作业元素;r为复杂度单位,当r=2时,复杂度的单位为比特(bit);Hm为第m个工作站的复杂度,m为工作站编号;km为第m个工作站包含的作业元素.
从复杂性测度的角度,以操作失误转化的信息量来描述系统复杂度可直接反映系统受多种不确定因素影响的程度.适用于不同类型操作,具有一定的通用性.以此对过程复杂度和整线复杂度进行研究,并应用于生产线平衡中,能够提高生产系统的适应能力和抗干扰能力.
1.3 基于Lempel-Ziv算法的整线复杂性测度
产品经过一系列的工作站进行生产操作最终成为成品,每个工作站的状态直接影响产品的生产质量,而产品依次流经各工作站可以等同为一段时间序列.待作业元素分配至各工作站后,由作业元素的失误率核算各工作站的可用度.通过各工作站的可用度计算得到的整线复杂度可以表示产品自上线到下线过程保持完全正确状态的复杂程度,也能够反映生产线整线的稳健状态和可靠程度,所以应用针对时间序列的Lempel-Ziv算法测度整线复杂度.
1.3.1工作站可用度计算
工作站可用度表示任一时刻工作站处于正常工作状态的概率,由工作站可用度测度得到的整线复杂度可以评价整线状态.由作业元素失误率计算各工作站可用度为
(3)
式中:Pm为第m工作站的可用度.
1.3.2粗粒化
设工作站可用度为序列P={P1,P2,…,PM},M为工作站总数,粗粒化就是将其重构为[0,1]序列S={s1,s2,…,sM},以便计算相应复杂度.
首先,求得序列P的平均值为
(4)

1.3.3整线Lempel-Ziv复杂度求解
计算序列S={s1,s2,…,sM}的复杂度,具体流程如图2所示.
(1) 初始化c(M)=1构造S、Q、SQ、SQP序列,S和Q代表两个子序列,SQ为Q排在S后由S和Q组成的序列,SQP为SQ去掉最后一个元素后的序列;
(2) 设S=s1,s2,…,sl,Q=sl+1,SQP=s1,s2,…,sl,判断Q是否为SQP的子串,若是,则S不变;
(3) 更新Q=sl+1,sl+2,SQP=s1,s2,…,sl+1,若否,则S=SQ,Q=sl+3,且c(M)=c(M)+1;
(4) 按步骤(2)和步骤(3)循环至S的最后一位为止,输出c(M)整线Lempel-Ziv复杂度.

图2 Lempel-Ziv复杂度计算流程Fig.2 The flow chart of Lempel-Ziv complexitycalculation
1.3.4整线复杂度归一化
为使整线复杂度具有可比性,对复杂度进行归一化处理.Lempel等证明了对属于[0,1]的序列几乎所有的c(M)都会趋向于一定值[16].序列S的长度为M,序列中不同元素的种类为α,则
(5)
式中:M→∞,εM→0,c(M)取上限.
(6)
计算归一化复杂度有
(7)
式中:cLZ(M)为反映生产线整线复杂程度的归一化度量.绝对简单系统的复杂度应该为0,随机系统的复杂度最大,定义为1.
信息熵是与状态和概率紧密联系的,适用于描述作业时间波动,又不局限于特定的分布,对不同类型工作站有一定通用性.Lempel-Ziv算法则侧重于反映状态之间的变化速率,即各工作站状态的无序程度,可以反馈生产线在当前性能状态下的稳定保持能力.两者是相得益彰的复杂性测度方法,能更准确刻画不确定因素对生产线性能的影响程度.
1.4 生产线平衡模型的建立
设一生产任务由n个作业元素组成,待分配到M个工作站,作业元素之间遵循优先关系约束.为提高生产效率,均衡各工作站复杂度和降低整线复杂度,以平衡率最大、复杂度均衡指数最小和整线复杂度最小为目标建立平衡优化模型,即
(8)
(9)
Minw(x)=MincLZ(M)
(10)
约束条件为
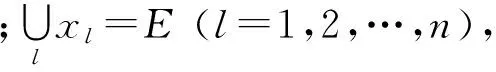
式中:f(x)为平衡率;g(x)为工作站复杂度均衡指数;cLZ(M)为整线复杂度;ti为第i个作业元素的作业时间;n为作业元素总个数;M为工作站总数;Tm为第m个工作站分配的作业元素作业时间之和;C为生产线预设工作节拍;j、l、y、z为作业元素的编号,xj、xl、xy、xz为第j、l、y和z个作业元素;E为作业元素集;N为优先矩阵.
2 算法设计
为求解优化模型,采用遗传算法并对优化策略进行改进,图3所示为遗传算法求解流程图.

图3 改进的遗传算法流程图Fig.3 The flow chart of improved genetic algorithm
具体优化策略如下:
(1) 将优先关系转化为优先矩阵,并定义初始参数,如初始种群规模、交叉概率、变异概率等,以实数编码方式生成染色体.
(2) 采用考虑作业元素优先关系和约束条件的种群初始化策略.生成优先级别最高的作业元素集,并随机排序放入染色体,删掉已分配作业元素,再次选取待分配元素中优先级别最高的作业元素集,随机排序放入染色体后部,如此反复直至所有作业元素分配完,生成一条染色体,循环生成一定数量的初始种群.
(3) 分配作业元素至工作站.首先从初始种群中选取染色体,并按基因顺序依次分配作业元素至工作站,当工作站满,则开启新工作站,继续按基因顺序分配染色体中未分配的作业元素至新工作站,如此循环依次将所有作业元素分配完毕,最终输出作业元素划分.
(4) 采用预先判别约束条件的交叉变异策略.交叉操作首先选取父染色体和母染色体,随机生成小于n的随机数d,则从第d位开始,父染色体的后半部分基因按母染色体中的基因顺序排列,母染色体的后半部分基因按父染色体中的基因顺序排列.变异操作首先选取父代染色体,随机生成小于n的随机数e,从第e位开始,后半部分采用初始化种群方法生成.交叉操作后子代的顺序继承了父代和母代顺序,所以仍然满足约束条件.变异操作按初始化方法生成,子代也满足约束条件.
(5) 建立适应度函数,编制计算机程序进行迭代求解多目标优化模型,最终得到满足适应度函数收敛精度的解,即平衡率最大,复杂度均衡指数最小和整线复杂度最小的作业元素最优划分.
适应度函数的表达式为
(11)
3 实例验证
某车企的发动机装配线包含109项作业元素、相应作业时间及失误率如表1所示.目标是根据生产计划将整线节拍控制在22 s以内,寻求最大平衡率、均衡各工作站的复杂度并降低整线复杂度.

表1 作业元素的作业时间及失误率Tab.1 Operating time and failure rate of operations
作业元素遵循的优先关系约束由优先关系图表示,如图4所示.数字表示作业元素序号,箭头连接两个作业元素,箭头所指作业元素为紧后作业元素,箭头之前的作业元素为紧前作业元素.根据优先关系图生成优先矩阵,可以读入到可执行程序进行运算.
3.1 求解作业元素最优划分
在MATLAB2013a中编制求解程序,以适应度值收敛至0.000 1的精度为终止条件,输出作业元素最优划分及各工作站复杂度,输出最优解,见表2.整线平衡率为0.931 5,复杂度均衡指数为0.137 1.
归一化过程序列长度应为无限大,实际采集的序列不可能为无限大.所以,有限序列的复杂度会被高估,甚至出现大于1的情况[17].本文采用的归一化过程是对两个等长序列进行比较,两个序列的评价尺度是相同的,所以计算结果不作为绝对复杂度来评价,而作为相对复杂度来比较序列复杂度的大小是正确可靠的.优化后整线复杂度为1.25 bit.
根据求解结果,各工作站的作业时间具备较均衡的分布,整线节拍控制在22 s以内.各工作站复杂度分布较均匀,总体在保证整线具有最高平衡率的情况下,各工作站的复杂度得到了平衡.能够避免由于工作站复杂程度不均,导致某些工作站失误率较高,频繁出现产品不合格下线的情况,最终提高了装配线的鲁棒性和稳定性,达到维持装配线稳定有序生产,有效应对装配过程中的干扰因素和突发状况的目的.

图4 优先关系Fig.4 Precedence relations表2 优化后作业元素划分方案Tab.2 Allocation results after optimization

m包含作业元素t(s)Hm11-2-3-4-5-6-7-819.70.17952919.40.1532310-11-12-13-1422.00.1782415-16-17-18-19-20-21-2221.30.1738523-24-25-26-27-28-29-3019.40.1659631-32-33-34-35-36-37-38-39-40-41-4221.00.1894743-44-45-46-47-48-49-50-5221.10.2036851-53-54-55-56-57-5817.80.1680959-60-61-62-6421.40.19971063-65-66-6719.60.15461168-69-70-71-72-73-7421.90.21011275-76-77-78-79-80-81-82-83-84-86-8719.30.18301385-88-89-90-91-9220.50.19751493-94-95-96-9721.30.18021598-99-100-101-102-103-104-10521.60.180916106-107-108-10919.10.1621
3.2 生产线平衡方案的对比
在不考虑复杂度的情况下,以平衡率最高为目标进行平衡,得到的作业元素划分方案如表3所示.
计算得到平衡方案的整线平衡率为0.931 5,复杂度均衡指数为0.382 8,整线复杂度为1.5 bit.
3.3 结果分析与讨论
优化前后各工作站作业时间分布对比如图5所示.优化前后各工作站复杂度分布对比如图6所示.表4为优化前后平衡方案的整线平衡率、复杂度均衡指数和整线复杂度.
生产线平衡通常以提高生产效率为目标,未考虑复杂度影响的平衡能够实现较高的平衡率.考虑复杂度进行的生产线平衡在寻求复杂度均衡指数最小和整线复杂度最小的同时,也能够保证平衡率不降低,平衡率达到0.931 5.

表3 优化前作业元素划分Tab.3 Allocation result of operations beforeoptimization

图5 各工作站作业时间分布对比Fig.5 Comparison of the workstations operation time

图6 各工作站复杂度分布对比Fig.6 Comparison of the workstations complexity表4 优化前后效果对比Tab.4 Comparison of the optimization performance

优化效果对比整线平衡率复杂度均衡指数整线复杂度/bit优化前0.93150.38281.50优化后0.93150.13711.25优化效果064.18%16.67%
优化前未考虑复杂度的影响,虽然平衡方案具有较高平衡率,第12、13工位复杂度偏离整线平均水平较大,复杂度均衡指数为0.382 8,表明各工作站负荷严重不均.优化后各工作站复杂度较均衡,复杂度均衡指数为0.137 1,优化效果明显,降低64.18%.
基于所提整线复杂性测度方法计算优化前后的整线复杂度.优化后整线复杂度为1.25 bit,比优化前降低16.67%,明显降低了装配线的整线复杂度.
针对作业时间波动的随机型装配线,基于信息熵的过程复杂性测度和基于Lempel-Ziv算法的整线复杂性测度应用到生产线平衡中,同时以平衡率最高、复杂度均衡指数最小和整线复杂度最小为目标进行的生产线平衡优化,能够输出同时具备生产效率较高、各工位负荷差异最小和整线复杂度最小的平衡方案,对生产线生产决策具有很好的指导作用.
4 结论
(1) 针对生产线生产过程中的不确定因素,提出了过程和整线复杂性测度方法.基于信息熵理论对作业元素复杂度和工作站复杂度进行定义,基于Lempel-Ziv算法测度了生产线整线复杂度.以平衡率最大、复杂度均衡指数最小和整线复杂度最小为目标构建多目标优化模型,通过改进遗传算法求解得到了作业元素最优划分方案.
(2) 实例验证表明,与未考虑复杂性的平衡方案进行对比,本文方法得到的平衡方案保证最高平衡率的同时,均衡了各工作站复杂度,整线复杂度明显降低.该方法从操作失误率角度出发,不同于以概率分布形式描述作业时间波动状况,可适用于不同类型工作站.另外,从系统角度降低了工作站状态差异对正常生产流程的干扰.
参考文献:
[1] 郑力, 江平宇, 乔立红,等. 制造系统研究的挑战和前沿[J]. 机械工程学报, 2010, 46(21):124.
ZHENG Li, JIANG Pingyu, QIAO Lihong,etal. Challenges and frontiers of manufacturing systems[J]. Journal of Mechanical Engineering, 2010,46(21):124.
[2] SAIF U, GUAN Z, LIU W,etal. Pareto based artificial bee colony algorithm for multi objective single model assembly line balancing with uncertain task times[J]. Computers & Industrial Engineering, 2014, 76(C):1.
[3] BATTAÏA O, DOLGUI A. A taxonomy of line balancing problems and their solution approaches[J]. International Journal of Production Economics, 2013,142(2):259
[4] DONG J, ZHANG L, XIAO T. A hybrid PSO/SA algorithm for bi-criteria stochastic line balancing with flexible task times and zoning constraints[J]. Journal of Intelligent Manufacturing, 2015, 92(6):1.
[5] ÖZCAN, U, KELLEGÖZ T, TOKLU, B. A genetic algorithm for the stochastic mixed-model U-line balancing and sequencing problem[J]. International Journal of Production Research, 2011, 49(6):1605.
[6] NAZARIAN E, KO J. Robust manufacturing line design with controlled moderate robustness in bottleneck buffer time to manage stochastic inter-task times[J]. Journal of Manufacturing Systems, 2013, 32(2):382.
[7] CAKIR B, ALTIPARMAK F, DENGIZ B. Multi-objective optimization of a stochastic assembly line balancing: a hybrid simulated annealing algorithm[J]. Computers & Industrial Engineering, 2011,60(3):376.
[8] 刘俨后, 左敦稳, 张丹. 随机作业时间的装配线平衡问题[J]. 计算机集成制造系统, 2014, 20(6):1372.
LIU Yanhou, ZUO Dunwen, ZHANG Dan. Assembly line balancing with stochastic operation times[J]. International Journal of Computer Integrated Manufacturing, 2014, 20(6):1372.
[9] 唐秋华, 林斌, 何晓霞,等. 基于随机机会约束规划的U型装配线平衡优化[J]. 计算机集成制造系统, 2016, 22(4):955.
TANG Qiuhua, LIN Bin, HE Xiaoxia,etal. Balancing optimization of U-shaped assembly lines based on stochastic chance constrained programming[J]. International Journal of Computer Integrated Manufacturing, 2016, 22(4):955.
[10] ELMARAGHY W, ELMARAGHY H, TOMIYAMA T,etal. Complexity in engineering design and manufacturing[J]. CIRP Annals—Manufacturing Technology, 2012, 61(2): 793.
[11] EFTHYMIOU K, PAGOROPOULOS A, PAPAKOSTAS N,etal. Manufacturing systems complexity: an assessment of manufacturing performance indicators unpredictability[J]. CIRP Journal of Manufacturing Science & Technology, 2014, 7(4):324.
[12] 何非, 饶运清, 邵新宇. 基于装配关系复杂性的装配线动态平衡问题[J]. 计算机集成制造系统, 2013, 19(1):29.
HE Fei, RAO Yunqing, SHAO Xinyu. Assembly line dynamic balancing problem based on assembly relationship complexity[J]. Computer Integrated Manufacturing Systems, 2013,19(1):29.
[13] SALVESON M E. The assembly line balancing problem[J]. Journal of Industrial Engineering, 1955,6(3):18.
[14] 刘雪梅, 贾勇琪, 兰琳琳,等. 基于多目标遗传算法的柔性加工线平衡优化[J]. 同济大学学报(自然科学版), 2016, 44(12):1910.
LIU Xuemei, JIA Yongqi, LAN Linlin,etal. Optimization of line balancing for flexible machining lines based on multi-objective genetic algorithm[J]. Journal of Tongji University (Natural Science), 2016, 44(12):1910.
[15] EFTHYMIOU K, MOURTZIS D, PAGOROPOULOS A,etal. Manufacturing systems complexity analysis methods review[J]. International Journal of Computer Integrated Manufacturing, 2016, 29(9):1025.
[16] LEMPEL A, ZIV J. On the complexity of finite sequences[J]. IEEE Transactions on Information Theory, 1976, 22(1):75.
[17] 刘峰涛. 宏微观交通运输系统的复杂性测度及其管控应用[D].天津:天津大学, 2007.
LIU Fengtao. Complexity measure of macroscopical & microcosmic transportation systems and its application to management & control[D]. Tianjin: Tianjin University, 2007.

