500 MPa箍筋混凝土梁间接荷载作用下的受剪性能
周建民, 蔡惠菊, 刘 东, 陈 阳
(1.同济大学 土木工程学院,上海 200092;2.同济大学建筑设计研究院(集团)有限公司,上海 200092)
对于混凝土梁的抗剪承载力计算,《混凝土结构设计规范》(GB 50010-2010)[1](下文称《规范》)的编制依据主要是普通强度钢筋混凝土梁在直接加载作用下的试验结果.但是在一般现浇混凝土结构中,荷载并不是直接加载在主梁上,而是通过次梁或板间接加载在主梁上,因而实际结构中的加载模式与试验中一般采用的直接加载模式有一定差别.目前,我国对于实际工程中混凝土梁受剪性能的研究还不充分,以往的研究主要集中在对低强钢筋混凝土梁的研究,没有关于高强箍筋混凝土梁在间接加载作用下的受剪性能的试验研究.应用500 MPa钢筋作为抗剪箍筋,降低用钢量,从而获得显著的直接和间接经济效益,具有重大意义.在对低强钢筋混凝土梁的研究过程中,Taylor的试验得出无腹筋梁间接加载的抗剪强度比直接加载降低0~70%[2].我国研究人员也得出在间接加载作用下钢筋混凝土梁抗剪承载力要低于直接加载作用下钢筋混凝土梁抗剪承载力,其降低程度为0~63.4%[3~5].同时,《规范》抗剪承载力计算公式并没有考虑直接加载梁与间接加载梁抗剪承载力的差别,对于间接加载梁,只是作了在集中力处附加横向钢筋的规定,并且是基于过去低强度箍筋混凝土梁试验研究成果.
在对配有500 MPa高强箍筋混凝土梁直接加载条件下抗剪性能研究的基础上[6],课题组另外进行了3根配有500 MPa高强箍筋混凝土梁的间接加载试验.试验目的在于分析配有500 MPa高强箍筋混凝土梁受力性能在间接加载作用下与直接加载作用下的异同;研究配有高强箍筋混凝土梁在间接加载作用下与直接加载作用下抗剪承载力的差别,并验证《规范》抗剪承载力计算公式对配有高强箍筋的混凝土梁在间接加载作用下抗剪承载力计算的适用性,以及《规范》中附加横向钢筋的构造措施能否适用于间接加载作用下高强箍筋混凝土梁.
1 试验概况
1.1 试件设计
参考以往研究人员进行的钢筋混凝土梁间接加载试验[3~4],本次试验设计了3根矩形梁,试验梁的具体参数如表1所示.B1~B3进行间接加载,B1-1~B1-3为同等条件下的直接加载混凝土梁[6],混凝土强度等级为C50,混凝土梁跨度为4 000 mm,两组梁纵向钢筋和箍筋强度均为500 MPa,截面尺寸为200 mm×400 mm,保护层厚度为25 mm.试件的截面尺寸(单位:mm)和配筋如图1所示,图中a为加载点至构件端部间的距离.
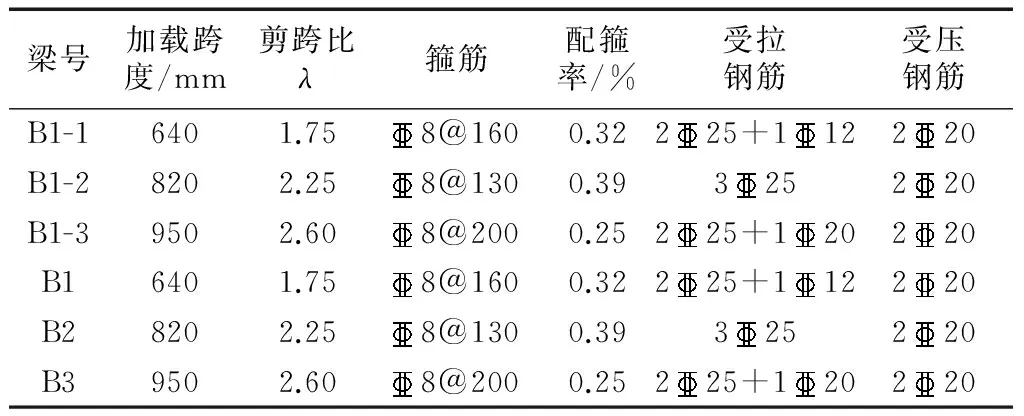
表1 试件参数Tab.1 The details of specimens
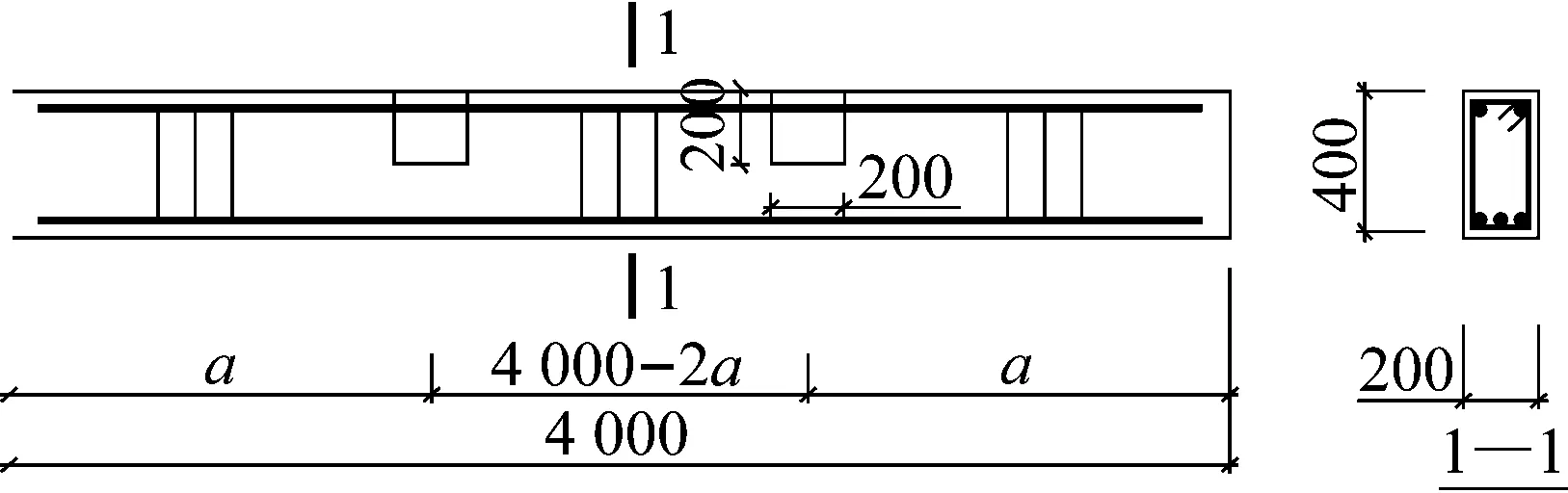
图1 试件尺寸(单位:mm)Fig.1 Dimension of specimens (unit: mm)
1.2 试验装置及加载制度
间接加载试验装置如图2所示,图中a′为加载点至支座间的距离.

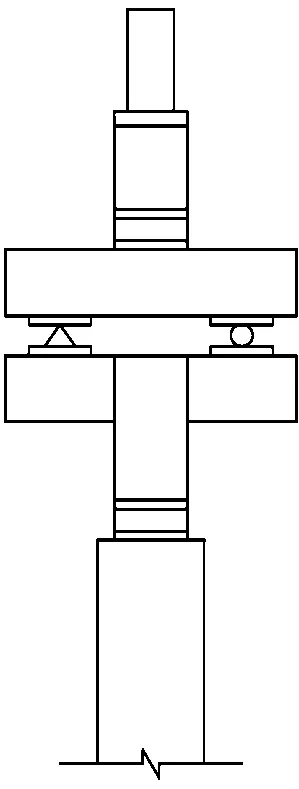
图2 间接加载试验装置(单位:mm)Fig.2 Test setup of indirect load (unit: mm)
本试验为单调静力加载,参照《混凝土结构试验方法标准》(GB50152—2012)[7]的相关规定.试验开始前先进行预加载.试验开始后,根据预估的极限荷载进行单调分级加载.间接加载矩形梁每级荷载约为预估极限承载力的7%.每级加载完毕持荷10min,使梁的变形趋于稳定,裂缝充分开展以及便于观测人员测量裂缝宽度.加载过程中注意捕捉斜裂缝的出现及发展趋势,当箍筋屈服后不再观测,并缓慢加载至梁破坏,并记录极限荷载.
1.3 试验测试内容
对于受剪构件,由于斜裂缝的出现位置具有随机性,因此为了量测斜裂缝处箍筋的点应变,于斜裂缝可能出现的位置所对应箍筋上布置电阻应变片.其可能出现斜裂缝的位置以加载点和支座的连线为准,如图3所示.因此,在梁前后左右共4个面布置箍筋应变测点.试验中,主要测量内容有:箍筋应变、试验梁极限荷载、纵向钢筋应变(分为跨中和剪弯段两个部分)以及试验梁挠度等.

图3 箍筋应变测点(单位:mm)Fig.3 The measuring points arrangement ofstirrup strain (unit: mm)
2 试验现象及结果分析
2.1 试验现象描述
高强箍筋混凝土梁,加载初期,试验梁表现为弹性.当加载到极限荷载的10%~20%时,梁出现正截面裂缝.当加载到极限荷载的20%~30%时,在剪弯段开始出现裂缝.一般说来,第一条裂缝大多在加载点对应的梁底附近出现.继续进行加载,斜裂缝稳定发展,从支座处一点点延伸到加载点处,并且裂缝宽度也逐渐增大,但正截面裂缝却发展缓慢.当加载到极限荷载的70%左右时,间接加载矩形梁,箍筋先于纵筋屈服并最终发生脆性的剪切破坏,而直接加载矩形梁在箍筋屈服的同时纵筋也开始屈服[6],最后纵筋与箍筋同时屈服,发生弯剪破坏或弯曲延性破坏.3根间接加载试验梁剪切破坏如图4所示.

aB1bB2

c B3图4 试验梁剪切破坏图Fig.4 Shear failure of test beam
2.2 试验梁荷载-跨中位移曲线
采用位移计测量梁在加载过程中的挠度变化,共有5个挠度测点,其中支座处两个,加载点两个,跨中一个.考虑支座沉降的影响,将跨中位移减去支座沉降得到梁跨中实际位移,结合既有试验整理试验结果[6],得到试验梁的荷载-跨中位移曲线如图5所示.

图5 试验梁荷载-跨中位移曲线图Fig.5 Curve of load mid-span displacementof test beam
2.3 试验梁抗剪承载力
计算结果采用《规范》中钢筋混凝土梁受剪承载力计算公式值[1].抗剪承载力理论计算结果与实测结果如表2所示.其中V1、P1分别为梁的理论计算承载力以及实际破坏荷载;降低程度为间接加载梁与同条件下直接加载梁试验对比结果.
由表2结果并结合计算可知,对于间接加载矩形梁,由《规范》公式所计算出来的抗剪承载力要高于实际的抗剪承载力,规范公式偏于不安全.这种偏差在小剪跨比时尤为明显,偏差达10%以上.随着剪跨比的增大,间接加载梁的破坏荷载与计算值的偏差逐渐减小.间接加载矩形梁极限承载力低于同等条件下直接加载梁,在小剪跨比时这种偏差会达到15%以上.间接加载矩形梁与直接加载矩形梁的偏差随着剪跨比的增大而逐渐减小.当剪跨比为λ=1.75或2.25时,间接加载梁的破坏荷载明显低于直接加载梁.当剪跨比为2.6时,间接加载梁与直接加载梁的破坏荷载大体相同.
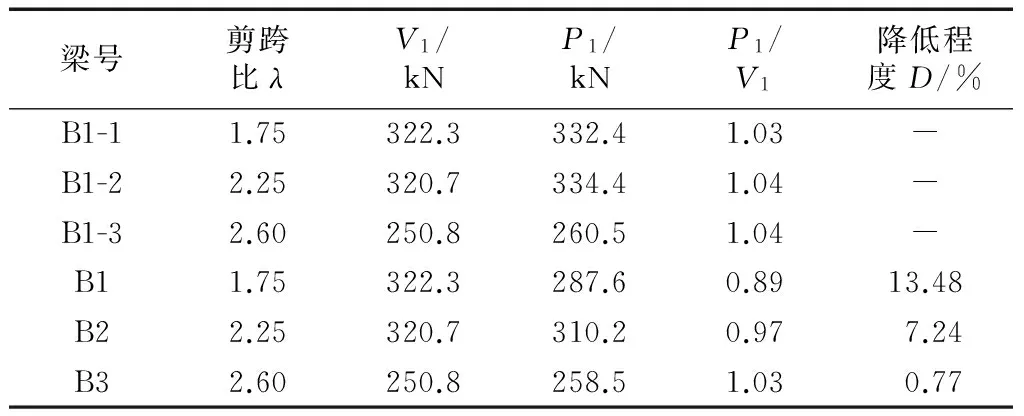
表2 理论计算与实际抗剪承载力对比Tab.2 Comparison between theoretical calculationand actual shear bearing capacity
3 间接加载下梁抗剪承载力分析
3.1 混凝土梁ABAQUS有限元模拟
为明确剪跨比与配箍率对间接加载混凝土梁抗剪承载力降低的影响,考虑对现有试验梁进行ABAQUS有限元模拟计算[8],明确适用本次试验的材料的本构关系及模型参数,以便代替试验来模拟不同剪跨比及配箍率情况的梁在直接加载和间接加载作用下的差别.
混凝土本构模型采用塑性损伤模型,钢筋混凝土采用分离式模型,且假定钢筋与混凝土之间黏结良好,变形连续,不考虑钢筋和混凝土之间的黏结滑移关系,以便得到比较准确的结果.本次有限元模拟采用位移加载方式,对有限元模型的加载点处施加一个比较大的位移,模拟结果容易收敛,且容易获得有下降段的稳定的荷载-位移曲线.有限元计算结果的极限荷载与对应的挠度与实测结果的对比如表3所示.
由表3可以看到,计算结果与实测结果极为接近,破坏荷载的计算结果与实测结果的误差基本在2%以内,构件达到破坏时加载点挠度的计算结果与实测值的误差也在4%以内,说明本文建立的有限元模型能很好地模拟实际加载情况,适用于高强箍筋混凝土矩形梁间接加载的斜截面受剪性能分析.
表3间接加载梁有限元计算结果与实测结果对比
Tab.3ComparisonbetweenFEMcalculationandactualshearbearingcapacityofbeamunderindirectload

梁号破坏荷载加载点挠度实测值Pu模拟值Pcs实测值Su模拟值ScsPcs/PuScs/SuB1576.9575.211.8912.130.9971.020B2620.3627.617.4518.041.0121.034B3517.1507.518.1417.940.9810.989平均值0.9971.014变异系数0.0120.019
3.2 间接加载下梁抗剪承载力分析
另外拓展了6种剪跨比下不同配箍率共18根高强箍筋混凝土梁,对这18根梁分别进行直接加载和间接加载模拟计算,矩形梁发生箍筋与纵筋屈服,剪弯段的斜截面混凝土先于纯弯段梁顶混凝土达到极限承载力时认为发生剪切破坏,结果如表4所示.其中,梁尺寸为200 mm×400 mm;λ为剪跨比;s为箍筋间距;ρst为箍筋配箍率;Pu1为间接加载梁破坏荷载;Pu2为直接加载梁破坏荷载;D为间接加载梁相对直接加载梁承载力降低程度,D=(Pu2-Pu1)/Pu2;De为平均降低程度.
表4模拟梁直接加载和间接加载破坏荷载对比
Tab.4Comparisonaboutfailureloadofsimulationbeamunderdirectloadandindirectload
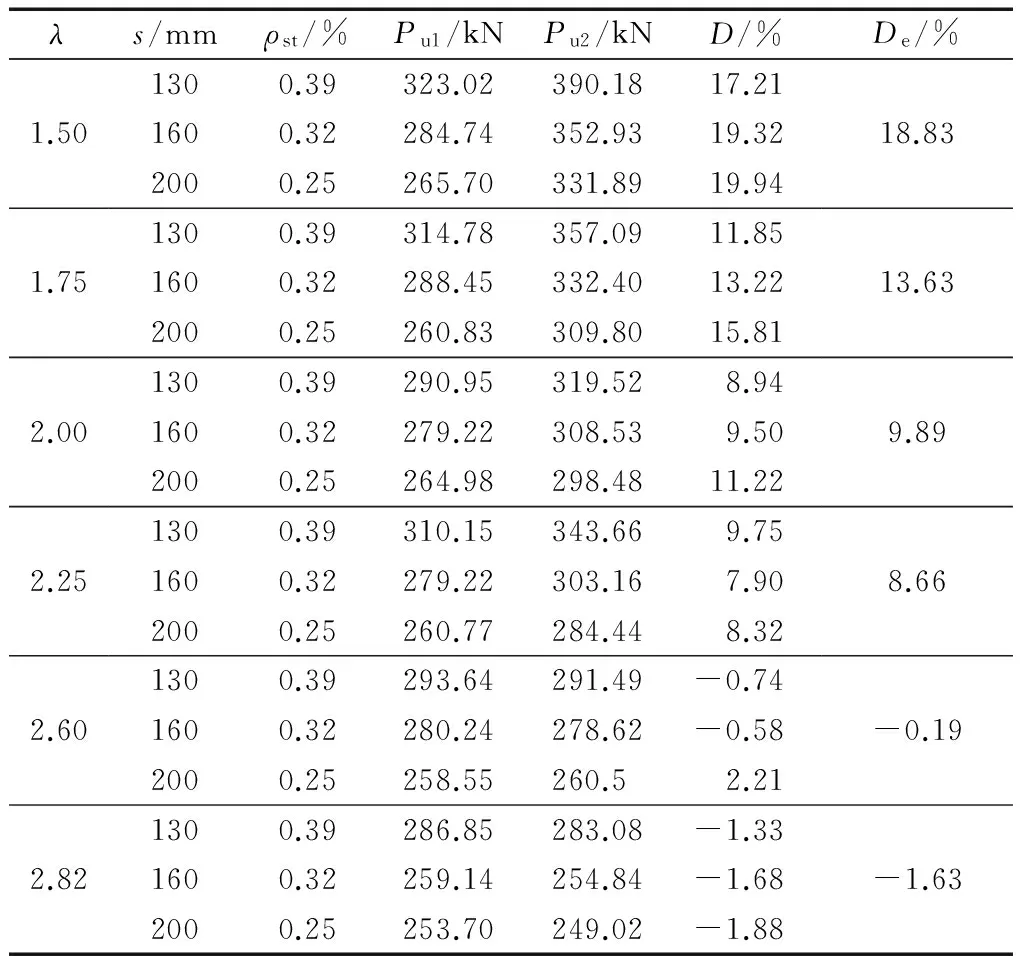
λs/mmρst/%Pu1/kNPu2/kND/%De/%1.501.752.002.252.602.821300.39323.02390.1817.211600.32284.74352.9319.322000.25265.70331.8919.941300.39314.78357.0911.851600.32288.45332.4013.222000.25260.83309.8015.811300.39290.95319.528.941600.32279.22308.539.502000.25264.98298.4811.221300.39310.15343.669.751600.32279.22303.167.902000.25260.77284.448.321300.39293.64291.49-0.741600.32280.24278.62-0.582000.25258.55260.52.211300.39286.85283.08-1.331600.32259.14254.84-1.682000.25253.70249.02-1.8818.8313.639.898.66-0.19-1.63
由表4可知,随着剪跨比的增大,间接加载矩形梁抗剪承载力相对于直接加载的降低程度逐渐减小.当剪跨比大于2.6时,间接加载矩形梁的抗剪承载力与直接加载梁基本相同.另外,相同剪跨比下,随着配箍率的增大,间接加载承载力降低程度也会逐渐减小.
在直接荷载的作用下,对于剪压破坏的梁,临界斜裂缝开展到荷载垫板下部时,由于受到集中力产生的局部垂直压应力的约束作用而趋于稳定.随着荷载的增加,斜裂缝末端上部的混凝土由于受到双向压应力(弯曲压应力和局部垂直压应力)和剪应力的作用,最后导致剪压区混凝土在双向压应力作用下被压破坏.梁顶单元体受力状态及破坏现象如图6所示.

a单元体受力状态b破坏现象
图6直接加载矩形梁梁顶单元体受力状态及破坏现象
Fig.6Forcestateofbeamtopunitunderdirectloadandphenomenonofdestruction
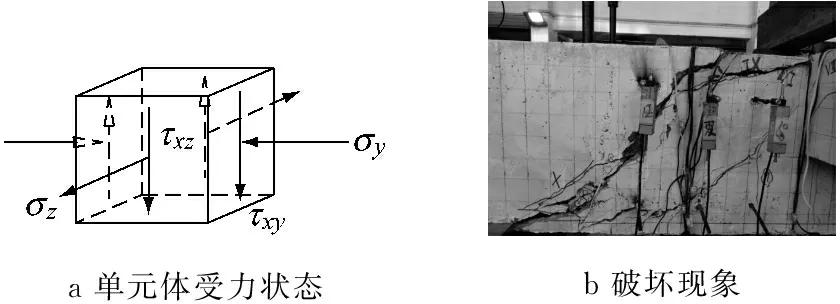
而在间接加载的情况下,由于荷载通过横向构件加于梁侧,而不是直接加于梁顶,因此就没有上述局部垂直压应力的约束,或者约束作用较小,甚至受到垂直拉应力的作用.混凝土的强度理论指出,混凝土双向受压比单向受压时的抗压强度高;而在拉压应力复合作用下,极限拉应力和压应力均比单向受力时大为降低.从强度理论的观点出发,可以说明间接加载的抗剪强度应低于直接加载的梁,试验研究结果也证实了这一点.而在间接加载时,因在原来的“斜压杆”范围内增加了局部垂直拉应力,不仅抗剪强度有所降低,而且破坏形态也有改变,梁顶混凝土由于少了垂直方向上的压应力而没有明显的压碎现象,斜裂缝大多会贯穿混凝土梁而发生破坏.梁顶单元体受力状态及破坏现象如图7所示.
a单元体受力状态b破坏现象
图7间接加载矩形梁梁顶单元体受力状态及破坏现象
Fig.7Forcestateofbeamtopunitunderindirectloadandphenomenonofdestruction
3.3 间接加载抗剪承载力折减系数
对于配箍率较大的梁,由于箍筋分担了更多的剪力,在剪跨比相同的条件下提高了加载梁的抗剪承载力,且能增加对混凝土的约束作用,所以间接加载梁的破坏荷载相对于直接加载梁降低程度更小.
王祖华也得出了类似的结论.王祖华通过对41根普通钢筋混凝土简支梁的对比试验研究发现[3],间接加载梁在小剪跨比下抗剪承载力降低较多,在大剪跨比下基本没有降低.研究发现,间接加载梁位于受拉区时最为不利,其承载力降低最多,相对于直接加载其承载力降低程度为50%~60%.分析其原因可能是由于破坏处单元体受双向垂直拉应力导致其承载力大大降低.并提出了加载梁位于受拉区时抗剪承载力降低公式如下:
(1)
式中:D为承载力降低程度;μRg/Ra为配箍特征,μRg/Ra=100ρst,ρst为配箍率;a/h0为计算剪跨比.
对于18根有限元模拟配有高强箍筋混凝土间接加载矩形梁相对于直接加载矩形梁承载力的降低程度,采用式(1)进行计算,得到公式与理论值对比如图8所示(式(1)适用于剪跨比小于2.6的混凝土梁).
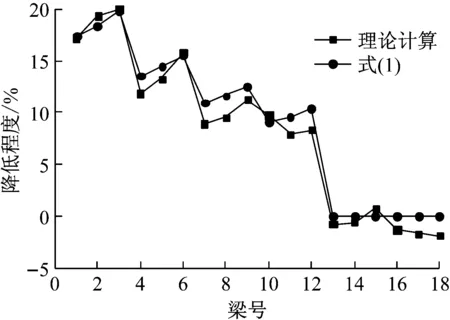
图8 公式与理论降低程度对比Fig.8 Comparison of reduction degree betweenformula and theoretical values
经研究发现,与普通箍筋混凝土梁相比,配有高强箍筋的混凝土梁在间接加载作用下加剧了抗剪承载力的降低状况,建议在计算配有高强箍筋混凝土梁在集中荷载间接加载状态下的抗剪承载力时对规范提出的公式乘以一个承载力降低系数,即
(2)
式中:D为承载力降低系数,D按式(1)计算取值;ft为混凝土抗拉强度设计值;b为梁的宽度;h0为梁的有效高度;fyv为箍筋抗拉强度设计值;Asv为梁配置在同一截面内箍筋各肢的全部截面面积;s为箍筋间距.
4 《规范》附加横向箍筋构造要求
我国《规范》用构造要求来处理低强钢筋混凝土梁间接加载问题.《规范》9.2.11条规定:位于梁下部或梁截面高度范围内的集中荷载,应全部由附加横向钢筋承担;附加横向钢筋宜采用箍筋[1],附加横向钢筋的总截面面积计算公式为:
(3)
式中:Asv为承受集中荷载所需的附加横向钢筋总截面面积;F为作用在梁的下部或梁截面高度范围内的集中荷载设计值;α为附加横向钢筋与梁轴线间的夹角.
按规范要求,在2h1+3b范围内进行附加箍筋布置,如图9所示.

图9 附加箍筋布置图Fig.9 Additional stirrup layout
当集中荷载在梁高范围内或梁下部传入时,《规范》从为防止集中荷载影响区下部混凝土的撕裂角度出发,规定应在集中荷载影响区2h1+3b范围内配置附加横向箍筋,用以弥补间接加载导致的梁斜截面受剪承载力的降低.集中荷载影响区2h1+3b范围内附加横向箍筋的配置,可以限制斜裂缝以及局部受拉裂缝的展开,能较好地发挥承剪作用.
为探究此构造要求能否弥补间接加载作用下配置高强箍筋混凝土梁斜截面抗剪承载力的降低,本文选取箍筋间距为200 mm,剪跨比为1.5、 1.75和2的3组梁进行验证,对加密后的梁用有限元程序进行验证,结果如表5所示.其中,箍筋直径为8 mm;箍筋补偿根数均为6根;箍筋为500 MPa钢筋,屈服强度为537.03 MPa.表中λ为剪跨比;Pu1为间接加载梁破坏荷载;Pu2为直接加载梁破坏荷载;Pu3补偿后承载力;D为间接加载梁相对直接加载梁承载力降低程度,D=(Pu2-Pu1)/Pu2;D1为间接加载梁相对补偿后承载力降低程度,D1=(Pu2-Pu3)/Pu2.
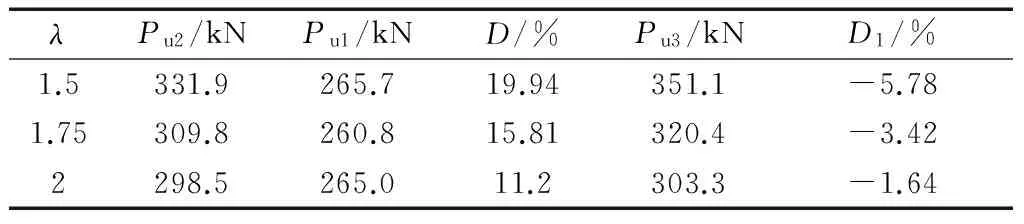
表5 箍筋补偿后混凝土梁的间接加载抗剪承载力Tab.5 The bearing capacity of beam under indirectload after stirrup compensation
前文有限元模拟发现,同等条件下的高强箍筋混凝土梁随着剪跨比的增加,间接加载相对于直接加载的折减系数逐渐减小.分析表明,随着剪跨比的增加,虽然梁的抗剪承载力较小,但梁的弯矩增长更快,故梁更倾向于发生弯曲破坏,梁的斜截面抗剪承载力降低程度D变小.
剪跨比小的情况下,剪力对抗剪承载力的影响较大,间接加载降低较多,附加横向箍筋作用大.由上表可以发现,按《规范》要求进行附加横向箍筋的补偿后,能明显提高间接加载梁的斜截面抗剪承载力.剪跨比大的情况下,剪力对抗剪承载力的影响较小,间接加载降低较少,附加横向箍筋作用减小.上述分析表明,当剪跨比大于2.6时,间接加载下高强箍筋混凝土梁的斜截面抗剪承载力与直接加载相比不再降低.故本文建议在对间接加载状态下配置500 MPa高强箍筋混凝土梁进行斜截面抗剪承载力设计时,可按《规范》构造要求进行附加横向箍筋的补偿.
5 结论
(1) 配置500 MPa钢筋的混凝土矩形梁在间接加载作用下与直接加载梁的抗剪破坏形式大体一致但也有所差别.当荷载达到极限荷载后,试验梁将以一种非常突然的方式发生破坏,箍筋的应力继续迅速增大,斜裂缝经过的箍筋甚至会出现颈缩现象,箍筋拉断,架立筋受压屈服.但是直接加载下的混凝土梁梁顶由于有垂直作用的压应力,剪压区混凝土会出现压碎现象.而间接加载梁的梁顶由于没有垂直压应力,甚至存在拉应力,所以破坏时梁顶混凝土受复杂应力开裂,没有混凝土被压碎的现象,斜裂缝会贯穿整个混凝土梁;
(2) 间接加载作用下高强箍筋混凝土矩形的梁抗剪承载力低于同等条件下直接加载的抗剪承载能力,抗承载力的降低程度主要受剪跨比和配箍率的影响,剪跨比越大,配箍率越大,承载力降低的越少.当剪跨比大于2.6时,间接加载矩形梁的抗剪承载力与直接加载梁相比基本没有降低;
(3) 配有500 MPa高强箍筋的混凝土矩形梁在间接加载作用下承载力会降低.按规范要求进行附加横向配筋补偿后,能够弥补间接加载下抗剪承载力的降低.
参考文献:
[1] 中国建筑科学研究院. 混凝土结构设计规范:GB 50010—2010 [S]. 北京:中国建筑工业出版社, 2010.
China Academy of Building Research. Code for design of concrete structures:GB 50010—2010 [S]. Beijing: China Architecture & Building Press, 2010.
[2] TAYLOR R. Some shear tests on reinforced concrete beams without shear reinforcement [J]. Magazine of Concrete Research, 1960, 12(36):145.
[3] 王祖华. 间接加载钢筋混凝土梁的抗剪强度[J]. 重庆建筑工程学院学报,1981(1):57.
WANG Zuhua. Shear strength of RC beams under indirect load [J]. Journal of Chongqing Institute of Architecture Engineering, 1981(1):57.
[4] 舒传谦,韦明辉. 间接加载钢筋混凝土悬臂梁抗剪强度探讨[J]. 贵州工业大学学报(自然科学版),1985(3):77.
SHU Chuanqian, WEI Minghui. Discussion on shear strength of RC cantilever beam under indirect load [J]. Journal of Guizhou University of Technology (Natural Science Edition), 1985(3):77.
[5] 王祖华,李阳明,张纪贵,等.钢筋混凝土梁的局部抗拉强度[C]//中国建筑科学研究院结构所.约束与普通混凝土强度理论及应用学术讨论会论文集. 北京:中国科学院出版社, 1987:438-446.
WANG Zuhua, LI Yangming, ZHANG Jigui ,etal. Local tensile strength of RC beams[C]// Structural Institute of China Academy of Building Research. Paper Compilation Academic Symposium on the Confinement and Ordinary Concrete Strength Theory and Application. Beijing: Chinese Academy of Sciences Press, 1987:438-446.
[6] 周建民,司远,王眺,等. 配置500 MPa箍筋的混凝土梁抗剪性能试验研究[J]. 同济大学学报(自然科学版),2016,44(1):45.
ZHOU Jianmin, SI Yuan, WANG Tiao,etal. Experimental study on shear behavior of concrete beam reinforced with 500 MPa stirrup[J]. Journal of Tongji University (Natural Science), 2016,44(1):45.
[7] 中国建筑科学研究院. 混凝土结构试验方法标准:GB 50552—2012 [S]. 北京:中国建筑工业出版社, 2012.
China Academy of Building Research. Standard for test method of concrete structures: GB 50552—2012[S]. Beijing: China Architecture & Building Press, 2012.
[8] 陈阳. 高强箍筋混凝土梁间接加载受剪性能试验研究及有限元分析[D]. 上海:同济大学,2014.
CHEN Yang. Experimental study on shear behavior and finite element analysis of concrete beam with high-strength stirrup under indirect load[D]. Shanghai: Tongji University, 2014.

