基于描述函数法的直线增程器动力学模型极限环分析
王 哲, 林炼炼, 臧鹏飞, 孙晨乐
(同济大学 新能源汽车工程中心, 上海 201804)
近年来,由于环保法规的日趋严苛以及化石能源危机,直线増程器(又称自由活塞直线发电机)的高效、环保、高能量密度以及燃料适用性等优势逐渐得到众多科研机构的关注.美国西弗吉尼亚大学、德国宇航中心、丰田汽车研发中心、纽卡斯尔大学、北京理工大学、同济大学等科研机构都对直线増程器进行了深入研究.多数机构通过数值仿真和试验方法来验证直线増程器动力学模型极限环的存在性,研究系统的运行状况与系统参数的关系[1-6],以及利用经验公式或者偏微分方程对进排气流动特性、燃烧特性、电磁特性等进行探究[7-9].少数机构通过能量平衡原理对直线増程器动力学模型的极限环进行分析[10].但是,数值仿真方法和能量平衡原理都无法在理论上对极限环的存在性和数量进行判断[11],而且由于这两种方法都是时域分析方法,对系统内部结构的分析略显不足.此外,能量平衡原理等解析方法具有较大局限性.
极限环为系统方程的相平面中闭合的孤立曲线,是非线性系统的特有性态.直线増程器的动力学方程为复杂的非线性方程,正是由于该方程具有极限环[10],所以直线増程器的活塞组件能够持续振荡进而带动直线发电机发电.复杂的非线性方程可能存在多个极限环.极限环分为3类:稳定极限环,不稳定极限环和半稳定极限环,其特性相当复杂[12].所以,深入分析直线増程器动力学系统极限环的特性至关重要.然而,到目前为止,相关的研究还较少.
本文采用描述函数法[12],在频域对系统的简化模型进行描述,并基于一试验样机参数,在复平面分析其极限环的存在性、数量以及稳定性,进而研究系统关键运行参数对极限环频率、幅值和相对稳定性的影响.分析结果能够为直线増程器的实际设计提供理论参考.
1 直线増程器动力学模型
直线増程器取消了曲柄连杆机构,将活塞连杆与电机动子同轴刚性固连.本文研究的直线増程器为点燃式的,其结构形式为双活塞式,如图1所示.其工作原理是通过左右两个燃烧室交替燃烧产生的高温高压气体推动活塞组件往复运动,进而带动直线发电机的动子切割磁感线输出电能.
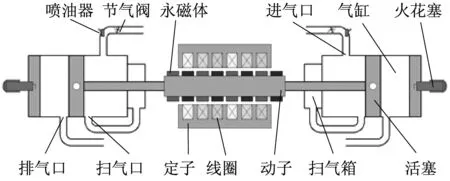
图1 直线増程器结构Fig.1 Configuration of linear range extender
将活塞组件视为质点P,取活塞组件在行程中点时其几何中心的位置为原点,将活塞组件的轴向视为x轴方向,令图1中的右方向为正方向,建立如图2所示的一维坐标系.质点P在x轴坐标系中的位置用坐标x表示.

图2直线増程器动力学模型坐标系
Fig.2Coordinateofdynamicmodeloflinear
rangeextender
根据直线増程器的系统结构和工作原理[1],忽略两端扫气箱的压力差,系统处于稳态发电时的动力学微分方程为
(1)
式中:m为活塞组件质量;Fs为库伦摩擦力;Fc为黏性摩擦力;Fp为左右两端气缸压力差;Fm为电磁力负载.
1.1 左右两端气缸压力差
由直线増程器的结构和工作原理可知
Fp=S(pl-pr)
(2)
式中:pl为左缸缸压;pr为右缸缸压;S为活塞横截面积.
当直线増程器处于稳态发电状态时,左右两缸的缸压pl和pr的模型是分段的.为了方便分析左右两端的缸压,做如下假设:
(1)左右两侧气缸燃烧室内的工质为理想气体,在整个热力学过程中工质的比热容为常数,不随温度变化,且无工质泄漏.
(2)直线増程器的压缩及膨胀过程均忽略传热损失,且将其简化为多变指数恒定的多变过程.
(3)直线増程器的燃烧过程忽略点火延迟,由于左右两缸的可燃混合气是使用火花塞点燃的,所以将燃烧过程视为瞬时的定容加热.
(4)直线増程器的扫气和排气过程为一个理想过程,忽略发动机的扫气和排气过程能量损失,认为气缸的压力始终与扫气压力相等.
(5)考虑了热量损失后,热量转化为有效功的过程视为可逆过程.
直线増程器的热力学过程可分为扫气过程、压缩过程、燃烧过程以及膨胀过程.根据发动机的热力学原理,现对每一过程的缸压模型进行详细分析.
1.1.1压缩过程缸压模型
由热力学的多变过程方程可得压缩过程的缸压计算公式为
(3)
式中:Vsc为压缩过程开始时刻气缸的容积;V为气缸的瞬时容积;n1为压缩过程的平均多变指数;pa为扫气压力.
Vsc=Vs+S(Xe+Xexh)
(4)
V=Vs+S(Xe+x)
(5)
式中:Vs为质点P的坐标x=-Xe时,左端活塞顶部与左缸顶部之间的间隙的体积;当x=Xe时,右端活塞顶部与右缸顶部之间的间隙的体积也为Vs.
将式(4)和式(5)代入式(3)可得,左缸在压缩过程的缸压为
(6)
(7)
1.1.2燃烧过程缸压模型

由式(6)可得
(8)
由热力学相关理论,最终可以得到prf的计算公式如下[13]:
(9)
式中:γ为可燃混合气的比热容比;Vi为燃烧时刻的左缸体积,可表示为
Vi=Vs+S(Xe-Xign)
(10)
Qin为燃烧的燃油释放的热量,可表示为
Qin=ξHμmf
(11)
式中:mf为喷油量;ξ为有效燃烧系数;Hμ为燃油的低热值.

由于直线増程器的结构左右对称,且左右两缸的喷油量相同,故可得
pl0=pr0
(12)
plf=prf
(13)
1.1.3膨胀过程缸压模型
由热力学的多变过程方程可得膨胀过程缸压的计算公式为
(14)
式中:Vse为膨胀过程开始时刻气缸的容积;V为气缸的瞬时容积;n2为压缩过程的平均多变指数.
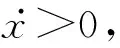
Vse=Vs+S(Xe-Xign)
(15)
V=Vs+S(Xe+x)
(16)
将式(15)和式(16)代入式(14)可得,左缸处于膨胀过程的缸压为
(17)
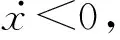
(18)
1.1.4扫气过程缸压模型
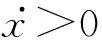
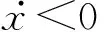
当x>Xexh时,左缸排气口开启,处于扫气和排气过程,这时左缸的缸压为
pl=pa
(19)
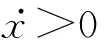
当x<-Xexh时,右缸排气口开启,处于扫气和排气过程,这时右缸的缸压为
pr=pa
(20)
综上,由式(2)~(20)可知,左右两端气缸压力差的公式是分段的,其图像大致如图3所示.由图3可判断其图像是关于原点对称的,所以只需列出图3

图3 Fp的图像Fig.3 Image of Fp
中实线部分的公式即可表示左右两端气缸压力差的总公式.图3中实线部分的公式如下:
(21)
其中
(22)
(23)
(24)
1.2 库伦摩擦力和黏性摩擦力
由摩擦学相关理论可知[14],库伦摩擦力的方向与速度方向相反,大小为恒定值Fs0,即
(25)
黏性摩擦力的表达式为
(26)
式中:k为黏性摩擦力系数.
1.3 电磁力负载
直线増程器的电磁力负载的可能形式有很多种,不失一般性,假设电磁力负载方向与速度相反,大小为恒定值Fm0[10,15],其表达式为
(27)
1.4 直线増程器动力学模型的拟线性近似
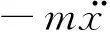
(28)
根据式(28),可以用图4表示系统的动力学模型.其中β为非线性单元的输出,线性单元传递函数G(jω)的表达式为
(29)
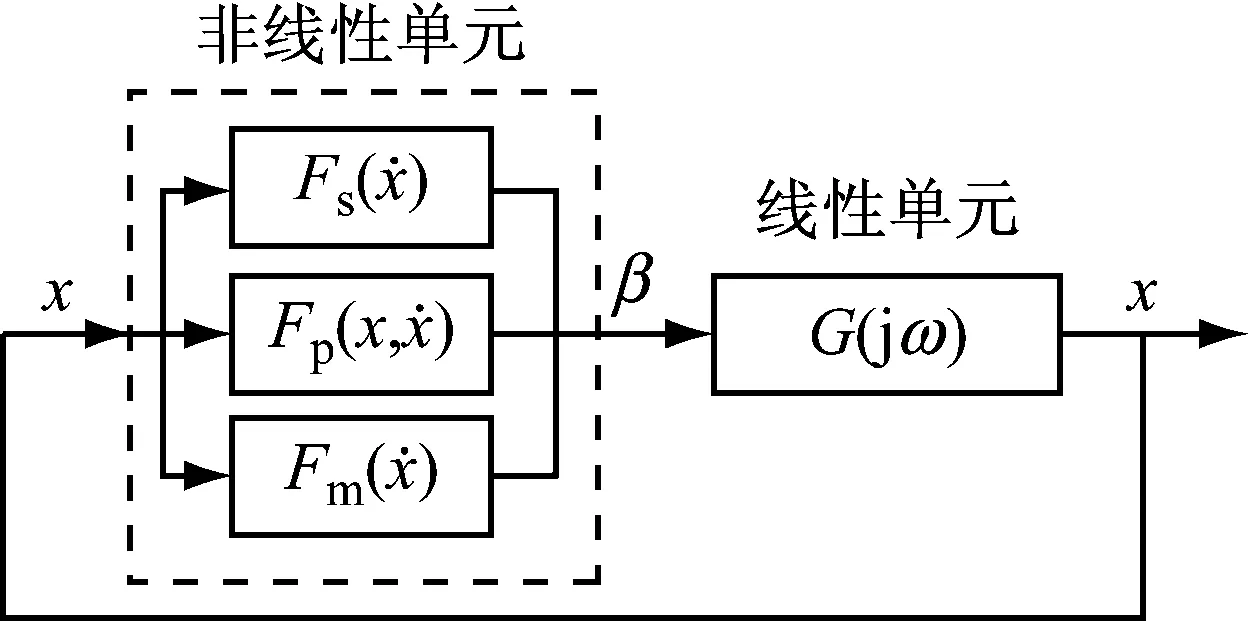
图4 动力学模型的反馈解释Fig.4 Feedback interpretation of dynamic model
由文献[12]可知,应用描述函数方法需要满足以下4个条件:
(1)非线性元件唯一.
(2)非线性元件为时不变.
(3)线性单元具有低通特性.
(4)非线性部分的输入和输出之间的函数的图像是关于原点对称的.
如图4所示,直线増程器动力学系统中虽然有多个非线性单元,但是,它们能够集成为单个非线性函数,因此满足条件(1).由式(21)、式(25)和式(27)可知,左右两端气缸压力差、库伦摩擦力和电磁力负载均为时不变的关于原点对称的函数,因此满足条件(2)和(4).由于实际系统中m>0且k>0,这使得线性单元G(jω)具有低通滤波的特性,而且其频率响应函数不存在共振峰值,因此满足条件(3).
综上,可以用图5中的非线性单元的描述函数N(A,ω)(A为幅值,ω为角频率)来替换该非线性单元,最终可以得到直线増程器动力学系统的拟线性近似,如图5所示.
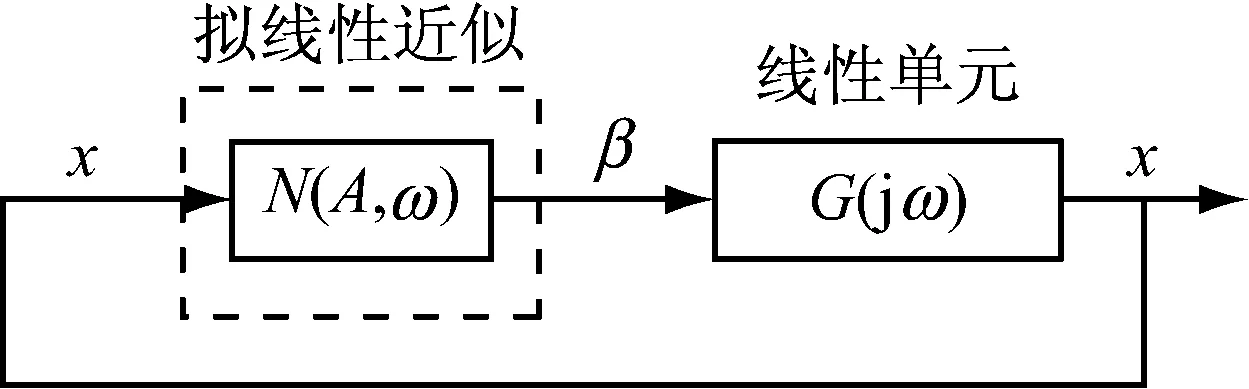
图5 动力学模型的拟线性近似Fig.5 Quasi-linear approximation of dynamic model
2 系统非线性单元描述函数
由式(25)和式(27)可知,Fs和Fm结构相似,可以合并为一项
(30)
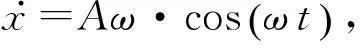
β(t)=βsm(t)+βp(t)
(31)
其中
βsm(t)=Fsm(Aωcos(ωt))
(32)
βp(t)=Fp(Asin(ωt),Aωcos(ωt))
(33)
根据描述函数的定义[12],图4中非线性单元描述函数N(A,ω)的表达式为
(34)
式中:a1和b1为β(t)的傅里叶级数中cos(ωt)项和sin(ωt)项的系数,其表达式为
t)d(ωt)
(35)

(36)
由式(31)可知,a1和b1都由两个分量的和组成
a1=asm1+ap1
(37)
b1=bsm1+bp1
(38)
其中
t)d(ωt)
(39)

(40)
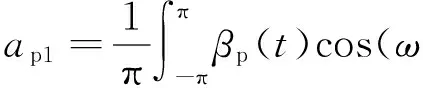
(41)

(42)
由式(30)、式(32)、式(39)和式(40)可以算出,bsm1=0,asm1的计算公式为
(43)
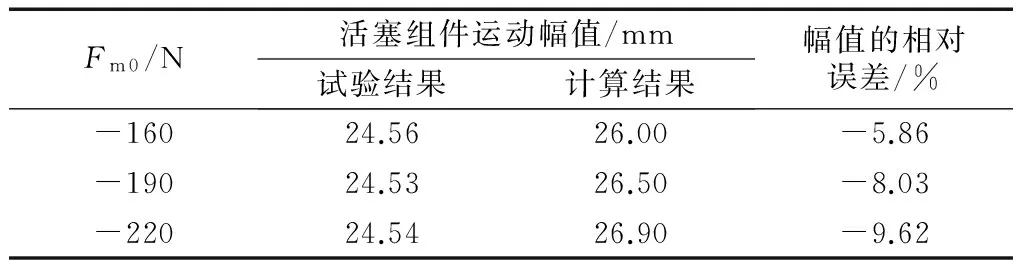
在实际系统中,若A≤Xign,则左右两气缸中的可燃气体都无法点燃;若A≥Xe,则活塞将同气缸盖发生碰撞.因此,A≤Xign和A≥Xe都会使系统无法正常运行,后面的讨论中只考虑Xign 由式(21)和式(33)可知,左右缸压差的输入输出函数图像如图6所示,βp(t)的表达式为 βp(t)= (44) 式中:γ1=arcsin(Xexh/A);γ2=arcsin(Xign/A). 图6 左右缸压差的输入输出函数Fig.6 Input/output function of pressure differencebetween left and right cylinders 将式(44)代入式(41)和式(42)并化简,可得ap1和bp1的计算公式如下: 由式(34)~(40)以及式(45)和式(46)可知,N(A,ω)的解析表达过于复杂,所以,后文将通过G(jω)和N(A,ω)的图像对直线増程器动力学模型的极限环进行分析.此外,由式(43)、式(45)和式(46)可看出,描述函数N(A,ω)只是幅值A的函数,即N(A,ω)=N(A),这为后面分析系统极限环带来了极大的便利. 假设图5所示的系统存在一个幅值为A且频率为ω的正弦振荡,则回路中的变量必须满足以下关系 N(A)G(jω)x=x (47) 等价于 (48) 再考虑实际系统的约束Xign 由文献[13]中的台架参数和试验结果可以得到系统各个固有参数的值如表1所示. 表1 样机参数Tab.1 Prototype parameters 设定Xign=24.7 mm,mf=2.53 mg,Fm0=300 N.根据式(29)和式(34),利用数值计算的方法画出G(jω)和1/N(A)的图像,如图7所示.其中两个箭头分别表示A和ω的增长方向. 图7 极限环的判断Fig.7 Detection of limit cycles 如图7所示,G(jω)和1/N(A)的图像在Xign 由图7可知,1/N(A)的图像是一段长度有限的曲线,且1/N(A)与G(jω)的图像在交点附近的夹角比较小,一旦系统参数发生变化,1/N(A)与G(jω)的图像可能不存在交点,即系统的极限环不存在.因此,需要进一步分析系统极限环存在时,喷油量mf和电磁力负载大小Fm0需要满足的条件.设定喷油量mf和电磁力负载Fm0分别在1.37~3.00 mg和0~450 N的范围内,其他参数与图7对应的参数相同,用同样的方法判断G(jω)和1/N(A)的图像是否存在交点.结果表明:喷油量与电磁力负载处于如图8所示带状阴影区域时,系统的极限环存在. 图8 Fm0mf图中极限环的存在区域 由G(jω)和1/N(A)的图像交点亦可求出极限环的近似频率和近似振幅.极限环的近似频率为G(jω)的图像上交点所对应的ω值,极限环的近似幅值为1/N(A)的图像上交点所对应的A值.因此,可以进一步研究喷油量及电磁力负载对极限环的频率和幅值的影响. 设定喷油量mf为2.43、2.53和2.63 mg,其他参数与图7对应的参数相同,G(jω)和1/N(A)的图像如图9所示.可以看出,随着mf的增大,1/N(A)图像向右下方移动,G(jω)和1/N(A)图像的交点所对应的的ω增大,A增大.同时设定电磁力负载Fm0为270、300和330 N,其他参数与图7对应的参数相同,G(jω)和1/N(A)的图像如图10所示.可以看出,随着Fm0的增大,1/N(A)图像向左上方移动,G(jω)和1/N(A)图像的交点所对应的的ω减小,A减小. 图9 喷油量mf对1/N(A)影响Fig.9 Influence of fuel injection quantitymf on 1/N(A) 图10 电磁力负载Fm0对1/N(A)的影响Fig.10 Influence of electromagnetic loadFm0 on 1/N(A) 设定喷油量mf和电磁力负载Fm0分别在1.37~3.00 mg和0~450 N的范围内,其他参数与图7对应的参数相同,用数值计算的方法计算极限环的近似幅值和近似频率,如图11和图12所示.由图11和图12可知,喷油量mf保持不变时,极限环的幅值和频率随着电磁力负载Fm0的增大而减小;电磁力负载Fm0保持不变时,极限环的幅值和频率随着喷油量mf的增大而增大. 图11 mf和Fm0对极限环幅值的影响 Fig.11InfluenceofmfandFm0onamplitudeoflimitcycle 图12 mf和Fm0对极限环频率的影响 Fig.12InfluenceofmfandFm0onfrequencyoflimitcycle 综上,可以得出如下结论:在极限环存在的情况下,电磁力负载Fm0的大小与系统极限环的频率和振幅均成负相关, 喷油量mf与系统极限环的频率和振幅均成正相关.这与文献[16]中的结论一致,验证了描述函数法的准确性. 如图13所示,记1/N(A)的图像上A=Xe对应的点与G(jω)图像的最短距离为D1,记1/N(A)的图像上A=Xign对应的点与G(jω)图像的最短距离为D2. 图13 极限环的相对稳定性参数Fig.13 Relative stability parameters of limit cycle 由奈奎斯特准则及其扩展可推知,当系统存在稳定的极限环时,若D1与D2同时增大,则系统极限环的相对稳定性提高;若D1或D2减小,则系统极限环的相对稳定性降低. 设定喷油量mf和电磁力负载Fm0分别在1.37~3.00 mg和0~450 N的范围内,其他参数与图7对应的参数一致,采用数值方法计算D1与D2的值.D1与D2的变化情况如图14和图15所示. 图14 mf和Fm0对D1的影响Fig.14 Influence of mf and Fm0 on D1 由图14和图15可知,若喷油量mf增大,则D1减小而D2增大;若电磁力负载Fm0增大,则D1增大而D2减小.这说明D1与D2存在矛盾,无法同时取到最大值.对比图11、图14和图15可得,当幅值大致等于25.2 mm时,D1与D2的值较为接近,此时系统极限环的相对稳定性较好. 对比图11和图14可得,在极限环幅值趋近于极限位置Xe=27.4 mm时,D1的值趋近于0,即极限环相对稳定性变差;对比图11和图15可得,在极限环的幅值趋近于点火位置Xign=24.7 mm时,D2的值趋近于0,极限环相对稳定性也变差.这表明,若极限环幅值接近Xe或者Xign,极限环的相对稳定性较差.在实际系统中一般会对上止点进行闭环控制,避免预定的活塞上止点接近点火位置或者气缸盖. 图15 mf和Fm0对D2的影响Fig.15 Influence of mf and Fm0 on D2 为了验证简化模型和描述函数法的准确性,基于文献[15]中的直线増程器试验台架进行了系统倒拖和燃烧试验.试验台架如图16所示.倒拖和燃烧试验是将直线増程器的电机切换为电动机状态,提供主动力拖动活塞组件运动,在达到燃烧条件后开始交替点燃左右缸中的可燃混合气. 图16 直线増程器试验台架Fig.16 Prototype of linear range extender 倒拖和燃烧试验可以获得直线増程器的活塞组件运动轨迹,将其与简化模型的仿真结果相对比,以此验证简化模型的准确性. 设定直线増程器喷油量为1.85 mg,点火位置为极限位置前3.5 mm,直线电机拖动力设置为160 N.相应地,令简化模型中喷油量mf=1.85 mg,Xign=23.9 mm,Fm0=-160 N.根据试验结果和简化模型仿真得到的数据,绘制活塞组件位移如图17所示.由图17可以看出,位移曲线吻合良好,验证了简化模型的准确性. 图17 试验和仿真结果对比Fig.17 Contrast of test and simulation results 由试验获得的活塞组件运动轨迹可以计算实际极限环的频率和幅值.将其与应用描述函数法计算出的结果相比较,以此验证描述函数法的准确性. 试验中直线电机拖动力分别设置为160、190和220 N;相应地,令简化模型中Fm0分别等于-160、-190和-220 N.保持其他参数与图17对应的参数相同.通过试验和描述函数法得到的极限环的频率和幅值如表2和表3所示. 表2 极限环频率的试验与计算结果对比Tab.2 Comparison of experimental and calculatedresults for limit cycle frequency 表3 极限环幅值的试验与计算结果对比Tab.3 Comparison of experimental and calculatedresults for limit cycle amplitude 由表2可知,试验得到的频率和描述函数法计算所得频率的相对误差在6%以内;由表3可知,试验得到的幅值和描述函数法计算所得幅值之间的相对误差在10%以内.由于活塞运动幅值变化的量级为10-1mm,而系统的测量误差较大且描述函数法为近似方法,所以试验结果中幅值的相对误差较大,变化趋势和计算结果也存在一定的差别.综上,试验结果进一步验证了简化动力学模型和描述函数法的准确性. 基于简化的直线増程器动力学模型,用描述函数表示模型中的非线性单元,在复平面中绘制G(jω)和1/N(A)图像,根据该图像分析了极限环的存在性、数量和稳定性,并研究了喷油量和电磁力负载对极限环的频率、幅值以及相对稳定性的影响.最后,通过试验验证了简化动力学模型和描述函数法的准确性和可靠性.得出的结论如下: (1)当喷油量和电磁力负载处于限制范围内时,直线増程器系统在物理约束的范围内存在唯一的极限环,并且这个极限环是稳定的. (2)直线増程器系统极限环的频率和振幅与喷油量成正相关,与电磁力负载成负相关. (3)在直线増程器稳态发电时,若活塞的上止点过于接近点火位置或者气缸盖,其极限环的相对稳定性变差. 参考文献: [1] 林滨滨,肖进,张磊. 基于Simulink和GT-Power的自由活塞发动机仿真 [J]. 内燃机与动力装置, 2017, 34(1): 17. LIN Binbin, XIAO Jin, ZHANG Lei. Simulation of free piston linear generator based on Simulink and GT-power[J]. Internal Combustion Engine & Power Plant, 2017, 34(1): 17. [2] 邓俊,叶晓倩,尹兆雷,等. 直线发动/发电机启动性能仿真研究 [J]. 同济大学学报(自然科学版), 2013, 41(4): 596. DENG Jun, YE Xiaoqian, YIN Zhaolei,etal. Simulation on starting performance of a linear engine generator[J]. Journal of Tongji University(Natural Science), 2013, 41(4): 596. [3] 尹兆雷,王哲,邓俊,等. 直线发动机起动及怠速燃烧特性仿真与优化 [J]. 同济大学学报(自然科学版), 2012, 40(10): 1554. YIN Zhaolei, WANG Zhe, DENG Jun,etal. Simulation and optimization on combustion characteristics of linear-engine system in starting and idle process[J]. Journal of Tongji University(Natural Science), 2012, 40(10): 1554. [4] SUN C, WANG Z, YIN Z,etal. Investigation of control method for starting of linear internal combustion engine-linear generator integrated system [C]∥SAE Technical Papers. Detroit: SAE International, 2015: 2015-01-1729. [5] GUO C, FENG H, JIA B,etal. Research on the operation characteristics of a free-piston linear generator: numerical model and experimental results [J]. Energy Conversion and Management, 2017, 131: 32. [6] JIA B, TIAN G, FENG H,etal. An experimental investigation into the starting process of free-piston engine generator [J]. Applied Energy, 2015, 157: 798. [7] YUAN C, FENG H, HE Y. An experimental research on the combustion and heat release characteristics of a free-piston diesel engine generator [J]. Fuel, 2017, 188: 390. [8] ZANG P, WANG Z, FU Y,etal. Investigation of scavenging process for steady-state operation of a linear internal combustion engine-linear generator integrated system [C]∥SAE Technical Papers. Detroit: SAE International, 2017: 2017-01-1087. [9] ZANG P, WANG Z, SUN C. Investigation of combustion optimization control strategy for stable operation of linear internal combustion engine-linear generator integrated system [J]. SAE Int J Alt Power, 2016, 5(2): 382. [10] 肖翀,左正兴. 自由活塞发电机动力学过程的非线性模型 [J]. 北京理工大学学报, 2008, 28(11): 966. XIAO Chong, ZUO Zhengxing. Nonlinear model and first order approximate solution of a free piston generator[J]. Beijing Institute of Technology, 2008, 28(11): 966. [11] 褚亦清. 非线性振动分析 [M]. 北京: 北京理工大学出版社, 1996. CHU Yiqing. Analysis of nonlinear vibrations [M]. Beijing: Beijing Institute of Technology Press, 1996. [12] SLOTINE J J E, LI W. Applied nonlinear control [M]. Beijing: China Machine Press, 2004. [13] 顾旺旺. 直线増程器控制仿真技术研究 [D]. 上海: 同济大学, 2016. GU Wangwang. Study on simulation technique of linear range extender control[D]. Shanghai: Tongji University, 2016. [14] GOTO S, MORIYA K, KOSAKA H,etal. Development of free piston engine linear generator system part 2: investigation of control system for generator [C]∥SAE Technical Papers. Detroit: SAE International, 2014: 2014-01-1193. [15] 孙晨乐,王哲,邓俊,等. 直线式增程器用直线ISG电机结构设计与优化 [J]. 汽车工程, 2014, 36(9): 1132. SUN Chenle, WANG Zhe, DENG Jun,etal. Structural design and optimization of linear ISG for linear range extender[J]. Automotive Engineering, 2014, 36(9): 1132. [16] 肖翀,左正兴. 自由活塞式内燃发电机动态仿真与特性分析 [J]. 农业机械学报, 2009, 40(2): 46. XIAO Chong, ZUO Zhengxing. Dynamic simulation and characteristic of free piston generator[J]. Transactions of The Chinese Society of Agricultural Machinery, 2009, 40(2): 46.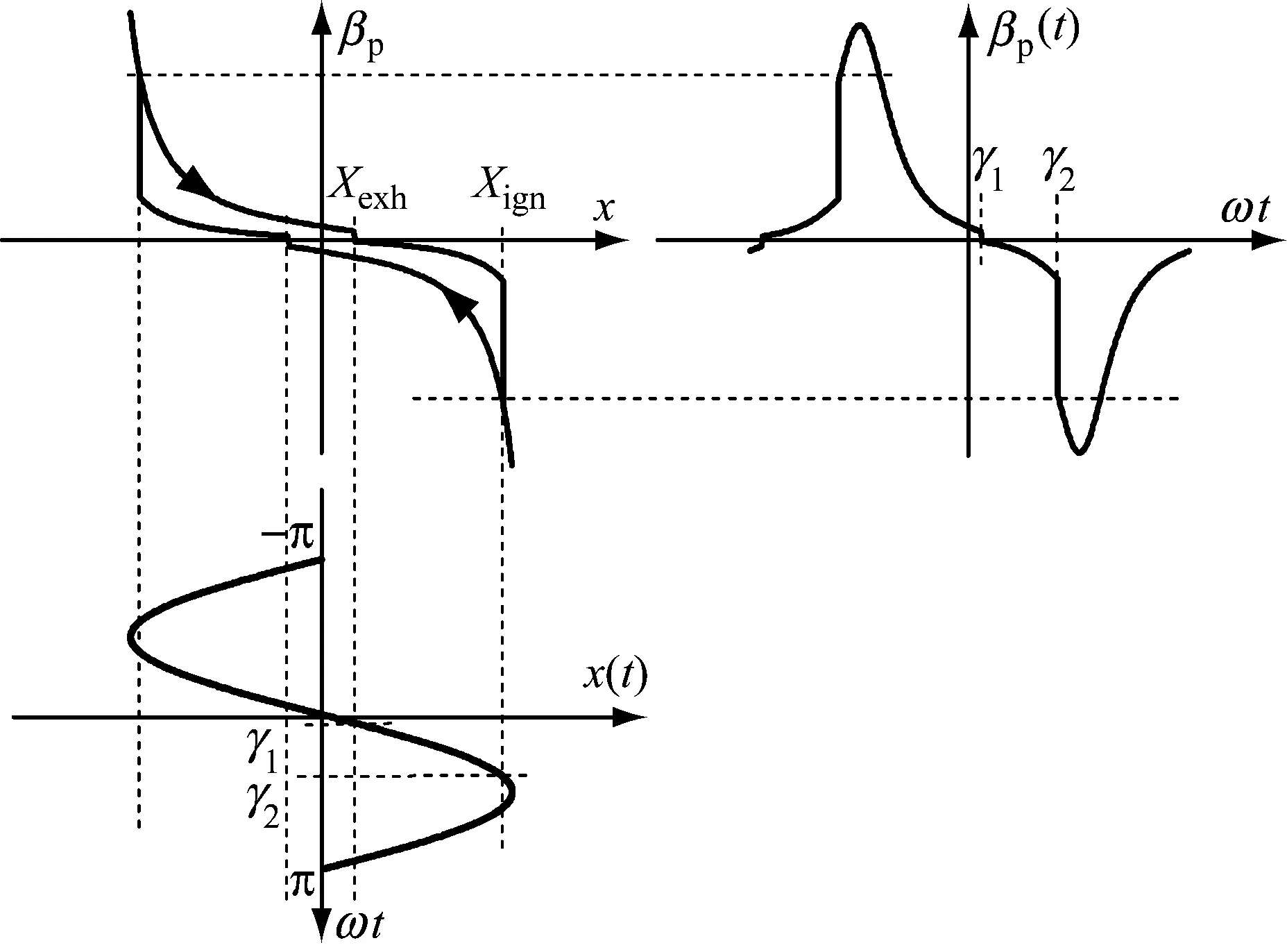
3 直线増程器系统极限环分析
3.1 直线增程器极限环的存在性和稳定性

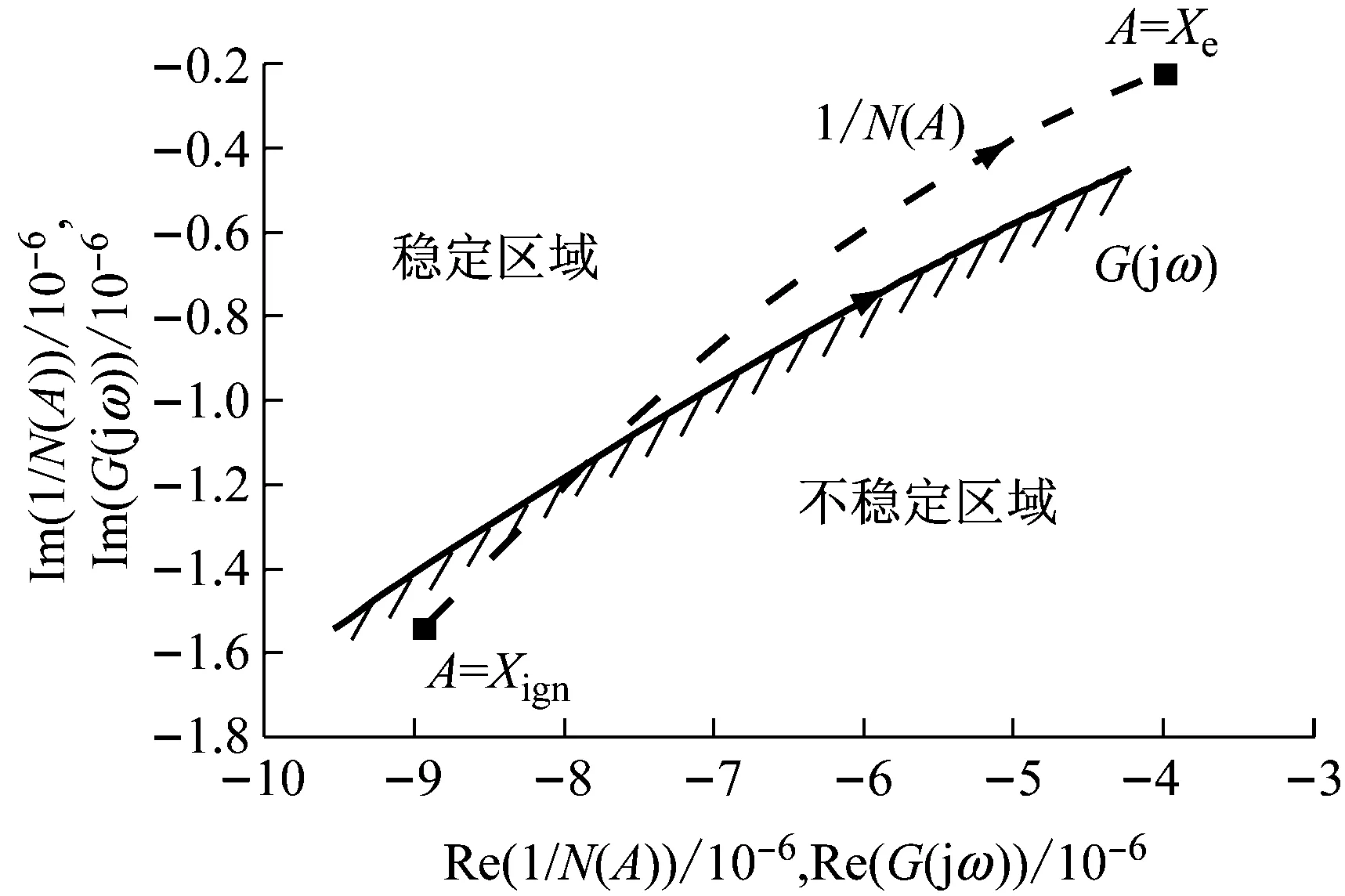


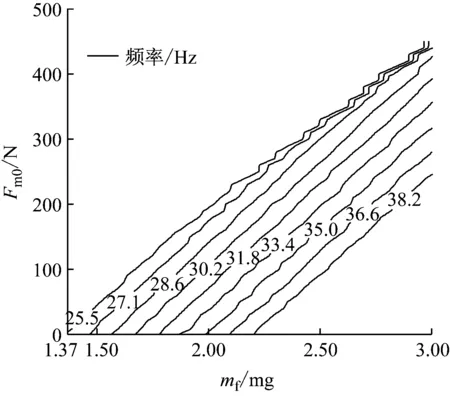
3.2 喷油量和负载对极限环幅值和频率的影响
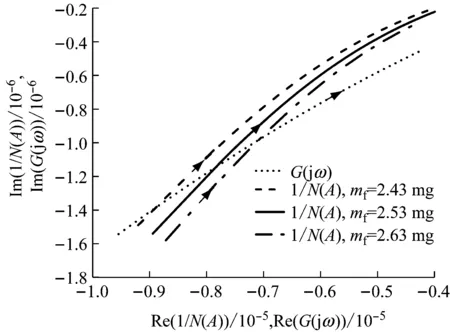
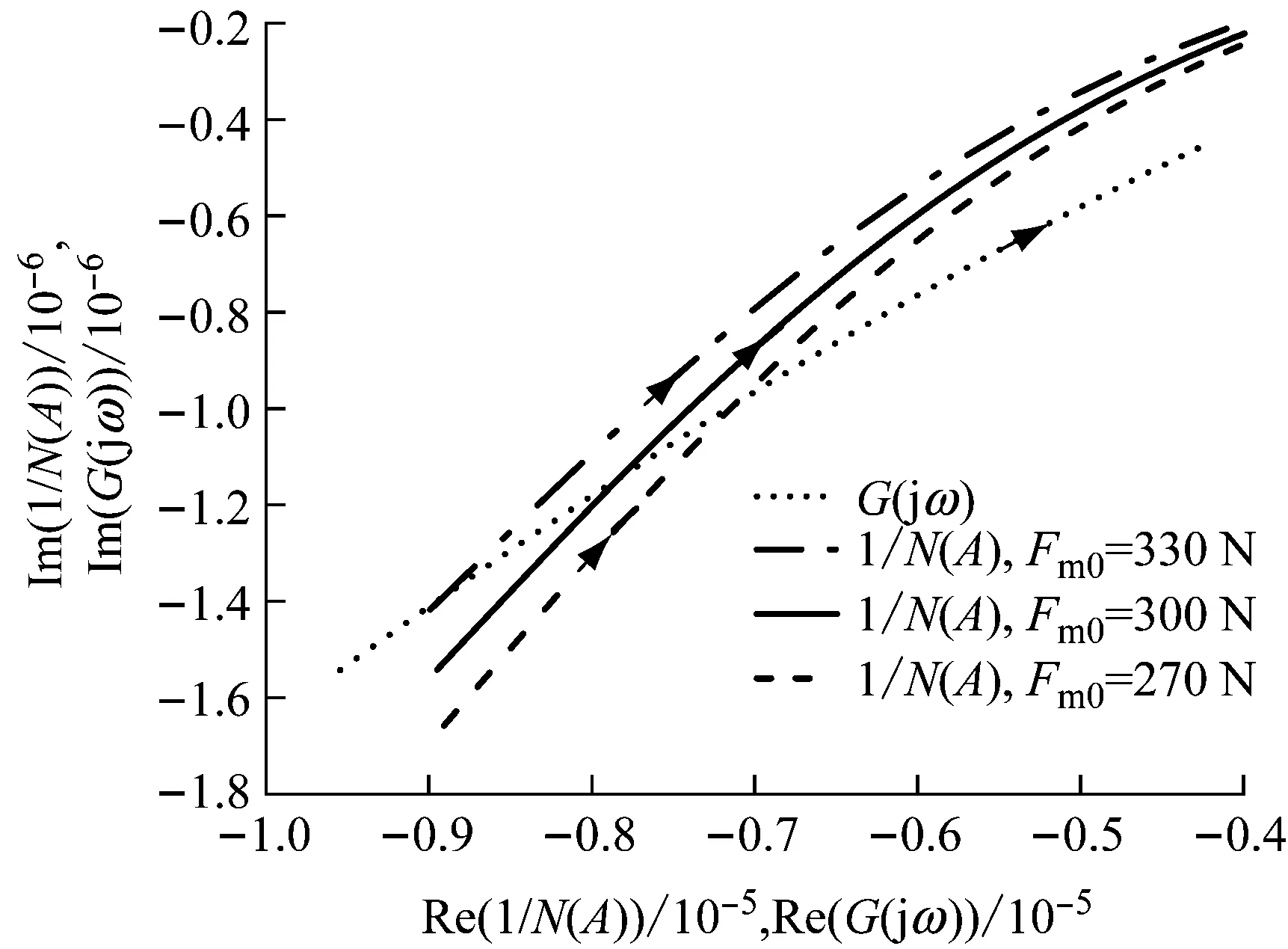
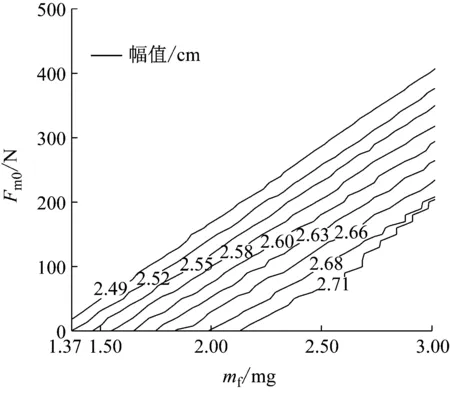
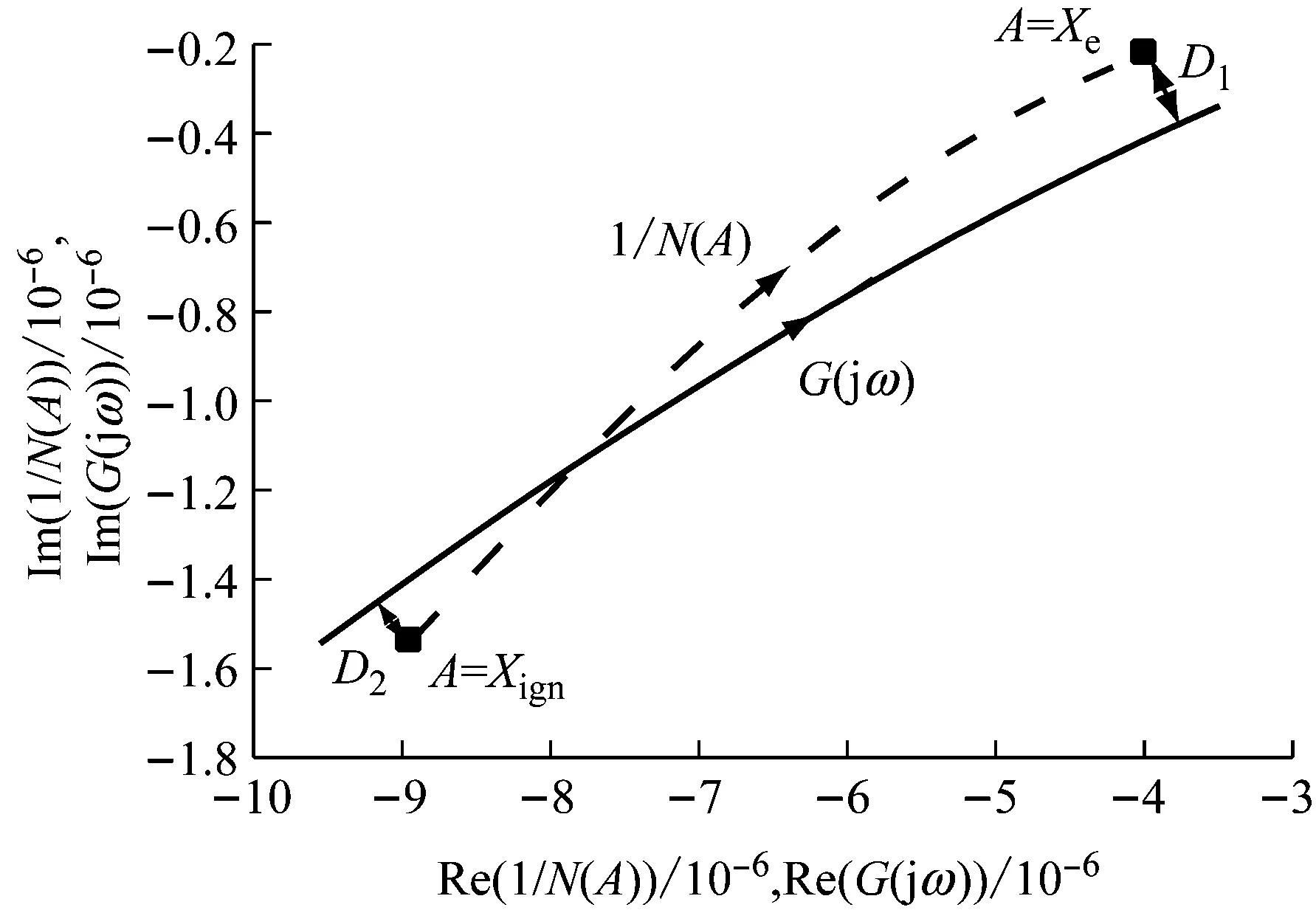
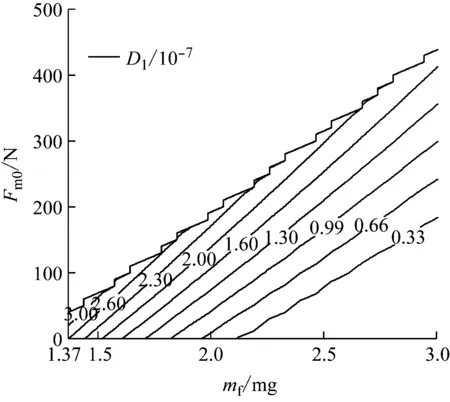
3.3 喷油量和负载对系统极限环相对稳定性的影响

4 试验验证

4.1 简化模型的试验验证

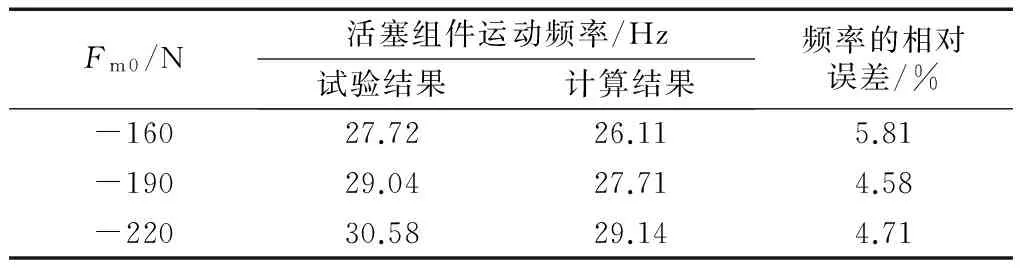
4.2 描述函数法计算结果的试验验证
5 结论

