浅谈对称性在曲线积分计算中的应用
(济源职业技术学院 河南 济源 459000)
曲线积分是微积分计算的一个重要分支,一般的曲线积分繁琐,麻烦,但当我们注意到问题的对称性,在积分计算中灵活运用,可大大简化计算,获得事半功效的成效.所以,很有必要探究对称性在积分计算中的应用,特别是在曲线积分、曲面积分中的应用。接下来本文将从两类曲线积分入手,综合阐述对称性在曲线积分计算中的应用。
1.对弧长的曲线积分
设有一弧形型构件占xOy面上的一段曲线L,设构件的质量分布函数为ρ(x,y),设ρ(x,y)定义在L上且在L上连续,求构件的质量。则有
定义1设L为xOy平面上的一条光滑的简单曲线弧,f(x,y)在L上有界,在L上任意插入一点列M1,M2,…,Mn-1把L分成n个小弧段 ΔLi=Mi-1Mi的长度为 ΔSi,又(ξi,ηi)是 ΔLi上的任一点,作乘积f(ξi,ηi)ΔSi,记 λ=max{ΔSi},ΔSi存在,且极限值与 L 的分法及(ξi,ηi)在 ΔLi的取法无关,那么称极限值为f(x,y)在L上对弧长的曲线积分,记为:
其中f(x,y)叫做被积函数,L叫做积分曲线。
注:
(2)将上述定义推广,可得空间曲线L上的第一型曲线积分:
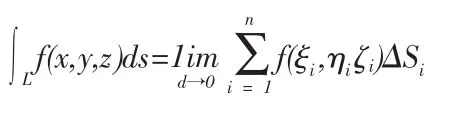
对弧长曲线积分的存在性:设f(x,y)在光滑曲线L上连续,那么(x,y)ds一定存在。
对弧长曲线积分的性质:
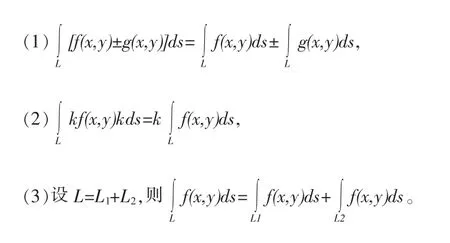
有了上述对弧长的曲线积分的定义,则上面的问题就能够用对弧长的曲线积分表示为
2.对坐标的曲线积分
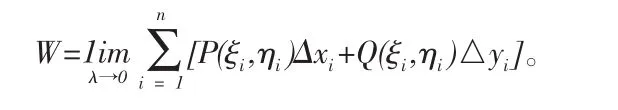
定义2设L=AB是xOy平面上的一条光滑有向曲线弧,P(x,y)、Q(x,y)在 L 上有界,用 L 上的点 M0(x0,y0),M1(x1,y1),…,Mn(xn,yn), 把 L分成 n 个小有向弧段 ΔLi=Mi-1Mi,设 Δxi=xi-xi-1,Δyi=yi-yi-1又(ξi,ηi)是ΔLi上的任一点,作乘积 P(ξi,ηi)Δxi,(i=1,2,···,n),并求和存在,且极限值与 L 的分法及(ξi,ηi)在 ΔLi的取法无关,那么称极限值为 P(x,y)在 L上对坐标 x的曲线积分,记为:
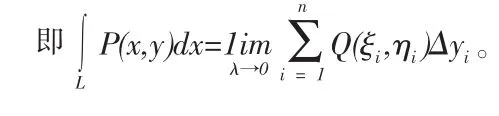
同理定义为 Q(x,y)在 L 上对坐标 y的曲线积分.P(x,y)、Q(x,y)称为被积函数,L叫做积分曲线。
上述定义可推广到空间曲线的情形:
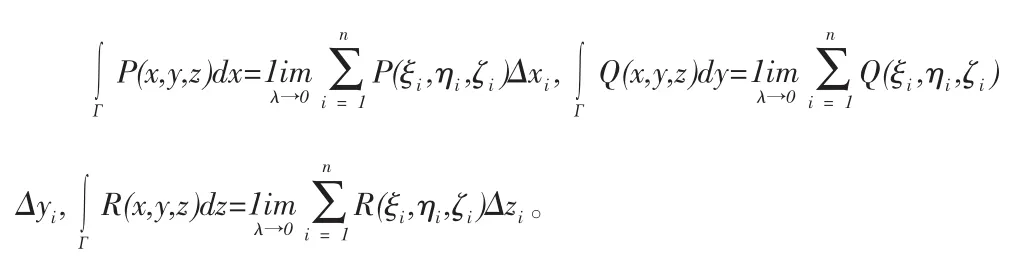
对坐标曲线积分的存在性:设有向曲线L光滑,P(x,y)、Q(x,y)在L上连续,则一定存在。
对坐标曲线积分的性质:
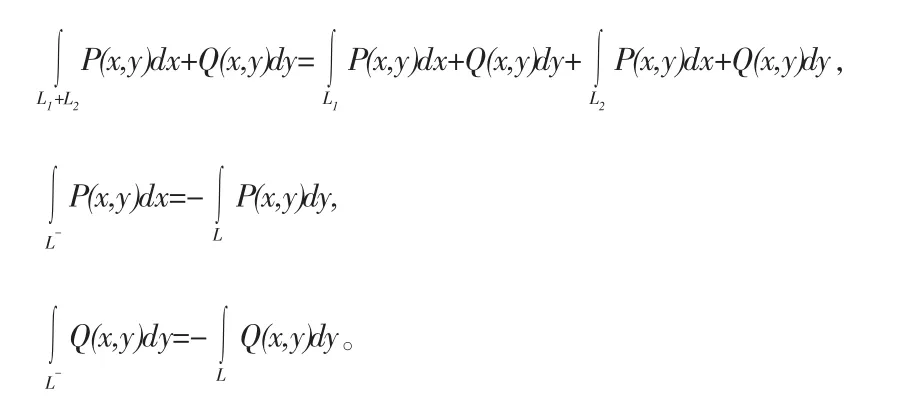
3.第一类曲线积分的对称问题
定义3设函数f(x,y)定义在二维光滑曲线上,
(1)如果 f(x,y)满足关系式 f(-x,y)=f(x,y)或 f(x,-y)=f(x,y),那么称 f(x,y)为关于x的偶函数或关于y的偶函数。
(2)如果 f(x,y)满足关系式 f(-x,y)=-f(x,y)或 f(x,-y)=-f(x,y),那么称 f(x,y)为关于x的奇函数或关于y的奇函数。
定义4设函数f(x,y,z)定义在三维光滑曲线上。
(1)如果 f(x,y,z)满足关系式 f(-x,y,z)=f(x,y,z)或 f(x,-y,z)=f(x,y,z)或 f(x,y,-z)=f(x,y,z),那么称f(x,y,z)为关于x的或y的或z的偶函数。
(2)如果 f(x,y,z)满足关系式 f(-x,y,z)=-f(x,y,z)或 f(x,-y,z)=-f(x,y,z)或f(x,y,-z)=-f(x,y,z),那么称f(x,y,z)为关于x的或y的或z的奇函数。
定理1设函数f(x,y)定义在二维光滑(或分段光滑)曲线L上,且曲线L关于 ox(或 oy)对称,则:
定理2设函数f(x,y,z)在三维光滑或(分段光滑)曲线Γ上可积,且曲线Γ对称于xoy(或yoz或zox)坐标面,则:
(1)当f(x,y,z)为关于z(或x或y)的偶函数时,则有(其中Γ1是Γ位于对称坐标面一侧的部分)。
(2)当f(x,y,z)为关于z(或x或y)奇函数时,则有
推论 设函数f(x,y)定义在二维光滑(或分段光滑)曲线L上,L对称于ox和oy轴,则:
(2)当f(x,y)是关于x和y中至少某一变量的奇函数时,有
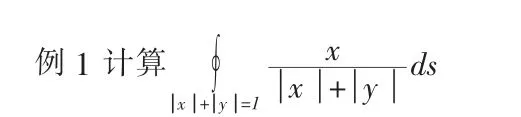
解因为积分曲线既对称于ox轴又对称于oy轴,且被积函数f(x,y)=是x的奇函数,故原式
注 此处除运用对称性之外,还涉及到用积分曲线方程化简被积函数的技巧。
解 注意到L关于x,y,z的对称性,则有:
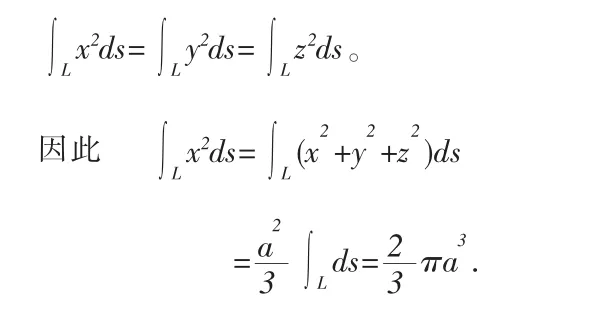
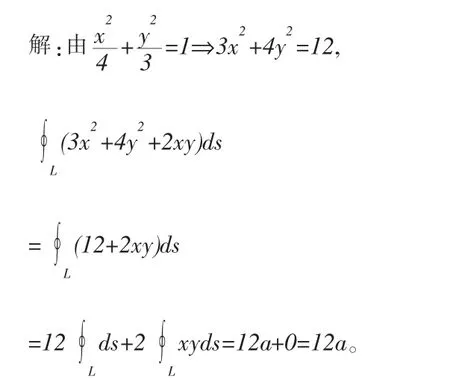
L关于y轴对称,被积函数xy关于x为奇函数。
4.第二类曲线积分的对称问题
定理3若L为xoy平面上关于x轴对称的一条有向光滑曲线弧,其方程是一双值函数,设为y=±y(x),(a≤x≤b).记 L1,L2分别为L位于x轴的上半部分与下半部分,L1,L2在x轴上的投影的方向相反,函数 P(x,y),Q(x,y)在 L 上连续,那么:
教材是教师教学和学生学习最重要的载体,某种程度上说,教材呈现的方式和内容决定了教师怎么教和学生如何学,因此通过对不同教材的比较研究,汲取各个教材的长处,对进一步深化课程与教学改革,落实核心素养目标具有重要意义.
解 经分析可知,此处的曲线积分合乎定理3,因而有:
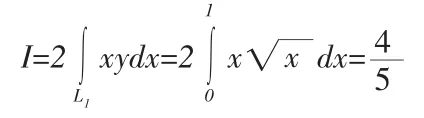
定理4设L为xoy平面上关于y轴对称的一条有向光滑曲线弧,奇方程为 y=y(x),(-a≤x≤a),记 L1,L2分别为 L 处于 y 轴的右半部分与左半部分,L1,L2在 x轴上的投影方向相同,函数 P(x,y),Q(x,y)在L上连续,那么:
定理5设L为xoy平面上关于原点对称的一条有向光滑曲线弧,奇方程为y=y(x),(-a≤x≤a),记 L1为L处于 y轴的右半部分与上半部分,L1,L2在x轴上的投影方向相同,函数P(x,y),Q(x,y)在L上连续,那么:
(1)函数 P(x,y),Q(x,y)关于(x,y)的偶函数 P(x,y)=P(-x,y),Q(x,y)=Q(-x,-y),则:
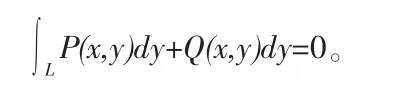
(2)函数 P(x,y),Q(x,y)关于(x,y)的奇函数 P(x,y)=-P(-x,-y),Q(x,y)=-Q(-x,-y)则:
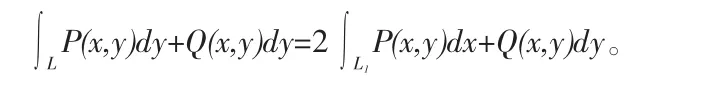
(4)当Q(x,y)关于x为奇函数时,则
定理6设L为xoy平面上具有轮换对称性的一条有向光滑曲线弧,奇方程为 y=y(x),(-a≤x≤a),函数 P(x,y),Q(x,y)在 L 上连续,那么:
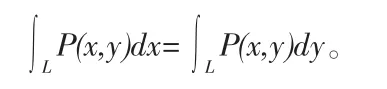
定理7设L为x,y,z上具有轮换对称性的一条有向光滑曲线弧,函数P(x,y,z)在L上连续,那么:
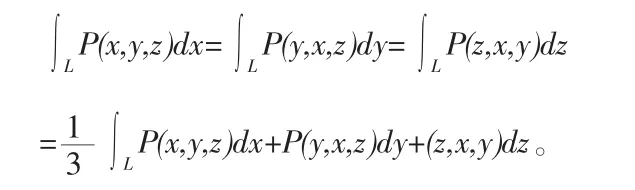
5.结论
通过以上介绍不难看出利用对称性计算曲线积分与曲面积分不仅是可行的,而且有时还可以起到简化计算的作用,在学习中可以充分利用对称性计算曲线积分与曲面积分,提高运算速度和效果,给学习带来很多方便.使得曲线积分更为简便、快捷,同时,也有利于避免因符号处理不当而导致的积分错误。
【参考文献】
[1]刘洁,戴长城.对称性在积分计算中的应用[J].邵阳学院学报:自然科学版,2008:23-27.
[2]刘福贵,鲁凯生.利用对称性计算第二类曲线积分和曲面积分的方法[J].武汉理工大学学报,2006:1069-1072.

