含突发E层的电离层模型建立及其在测高中的应用∗
罗欢肖卉
1)(中国人民解放军空军95519部队,遵义 563000)
2)(空军预警学院空天预警装备系,武汉 430019)
1 引 言
太阳的紫外辐射以及宇宙射线等与高层大气层相互作用,将使得该部分大气分子发生电离,形成一片准中性等离子聚集的区域,这个区域就是电离层.电离层的高度大致在60—1000 km,按照电子浓度的不同,电离层从下至上一般分为D层、E层、F1层和F2层[1],在中纬度地区,还经常出现不规则的突发E层(sporadic-E,Es层),在夏季出现Es层的概率更大[2].因为Es层是“突发”形成的,其很多特性和规律尚未探索清楚,目前对它的认识是:Es层是一片“电子云块”的集合体,电子浓度较高,不同的“电子云块”之间被弱电离气体所隔开,形成了网状的电薄层[3].由于Es层的“突发”特性以及高浓度电子的存在,会对高频射线的传播路径产生影响,引起射线产生反射或者散射现象[4],容易导致正常的高频射线探测任务失败,但正是因为这些特性的存在,又使得利用Es层进行高频射线近距离探测成为可能.中国幅员辽阔,但国土疆域恰好处于中纬度区域,所以Es层具有很高的出现频率,如何避免Es层对高频射线传播的不利影响以及如何有效地利用Es层进行通信和探测,都需要对Es层的规律和特性进行深入研究.
在利用电离层进行高频射线探测的研究领域,一个重要的方向就是估计被探测目标的空中高度.要实现目标的高度估计,需要对电离层建模.目前对电离层的建模方式主要有:卡普曼模型、准抛物模型(quasi-parabolic,QP)[5]和多层准抛物模型(quasi-parabolic segments,QPS)[6,7]、国际参考模型(International Reference Ionosphere,IRI)[8]及改进的IRI模型等[9,10].采用卡普曼模型对F2层模拟时,结果与实际电离层相差很大;IRI模型是根据全球地面观测站测得的电离层数据进行综合统计比对分析,采用计算机建模形成的全球通用电离层模型,但需要庞大的数据库和复杂的计算程序作支撑;QP和QPS模型采用准抛物线理论对电离层进行分层模拟,特别是QPS模型采用了准抛物线和反转抛物线相结合的建模方式,能够确保各层之间的电子浓度连续变化,是研究高频射线测高方法中常使用的模型[11].目前高频测高主要采用匹配域处理(matched-f i eld processing,MFP)方法[11,12],相关研究均只考虑了存在E层、F1层和F2层的情况,并未考虑出现Es层的电离层模型,而在对实测电离层数据统计时发现,Es层在中纬度区域有很高的出现概率,持续时间也较长,若仍采用以前的模型进行高度估计,误差会非常大.另外,在采用MFP方法估计目标高度值时,需要对高度区域进行遍历搜索,搜索时间很长,降低了实时结果的计算效率.
基于以上问题,本文对电离层实测数据进行分析,得到了实际电离层参数范围,基于实际参数,在QPS模型的基础上加入Es层及其连接层,建立了含Es层的电离层模型,并结合该模型提出了一种测量目标高度的快速方法.
2 含Es层的电离层结构及建模方法
2.1 研究含Es层的电离层模型的必要性
Es层一般突发在E层上,高度在90—140 km范围之间,厚度为1—2 km,水平方向的覆盖范围很广,可达几十公里到几百公里不等[13].关于对Es层的认识,普遍认为“风剪切”理论[14]是其形成的物理机理,该理论也得到很多学者的认可和发展[15,16].文献[17]采用地面电离层垂测系统的测量数据,对全球范围内绝大部分地区的电离层结构情况进行了分析,发现中纬度地区的Es层出现概率要明显高于其他地区,特别是北半球的中纬度地区,突发Es层的情况更加频繁.
为了分析中国电离层Es层突发情况,本文采用某型天波超视距雷达配备的电离层垂测站的实测数据,该垂测系统位于中国东部沿海某地,以15 min的间隔周期不间断地垂直探测上空电离层.图1给出的是2013年该系统获得的电离层Es层的截止频率(即该层最大等离子体频率)随季节的变化情况,截止频率的出现代表Es层已经突发形成.在分析数据时,春季为2—4月,夏季为5—7月,秋季为8—10月,冬季为11月—来年1月.从图中可以看出:Es层在全年的出现具有很强的季节性,夏季出现的频率最高,春、秋季次之,冬季出现的概率最小,即使在突发概率最小的冬季,其出现的平均时间也达到每天4 h;另外,Es层在白天的出现概率要高于在夜间的出现概率.
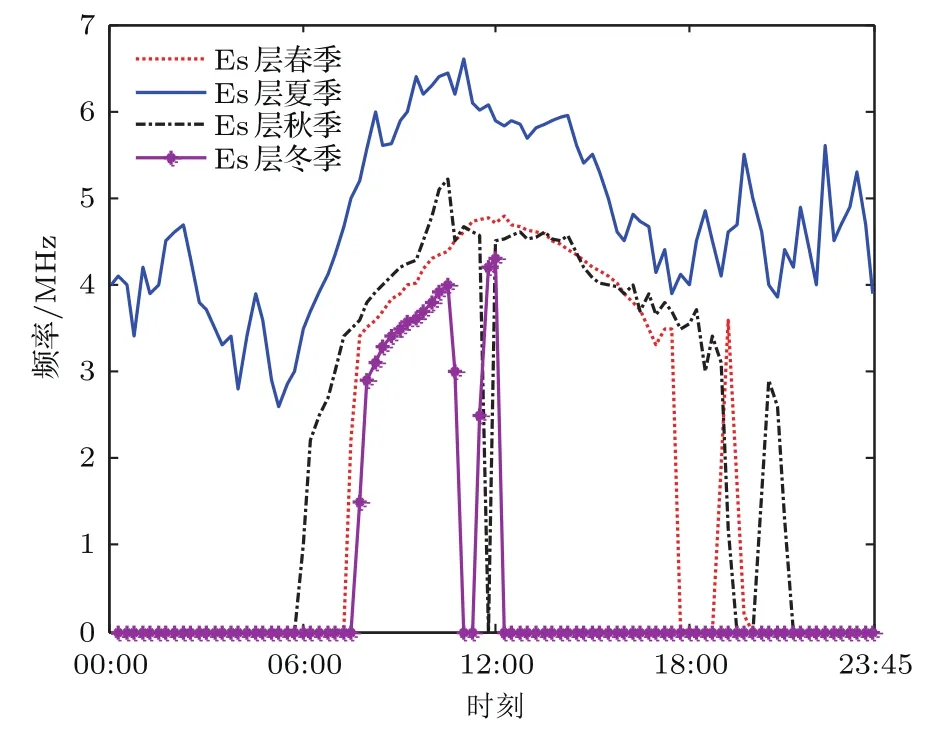
图1 Es层截止频率随季节的变化Fig.1. Seasonal variation curve of the cut-of ffrequency of Es layer.
本文的实测数据分析结果与文献[17]的统计结果一致,说明北半球中纬度地区的电离层Es层的突发情况具有较强的相似性,也说明Es层是北半球中纬度地区电离层研究不得不考虑的问题.同时图1的Es层季节曲线也表明,在夏季高发期,其截止频率最高能够达到6.5 MHz,如此高的截止频率对入射的高频射线具有很强的反射和散射作用,Es层的截止频率越高,对高频射线的反射越显著.若仍将电离层考虑为E层、F1层和F2层三层模型,在应用这个三层模型进行测高研究时就不再适用了,因为当实际突发Es层时,三层模型认为高频射线在某个发射仰角下是经E层反射的,但实际情况是该射线在达到E层前,已经被截止频率更高的Es层反射了,结果就造成了模型失配,最终导致目标高度估测失败.所以,对实测电离层数据进行分析并统计出参数结果,建立一种适用于高频射线测高方法研究的含Es层的电离层模型显得尤为重要.
2.2 含Es层的电离层模型
由于电离层QPS模型能够保证各分层之间的电子浓度连续变化,我们仍然以QPS模型为基础建立含Es层的电离层模型.
利用QPS模型,电离层中的单层电子浓度分布为[6]
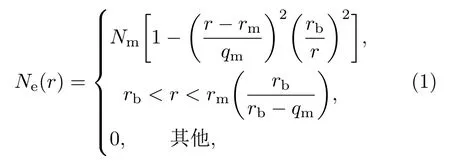
其中Ne(r)是电子浓度,r是电离层高度,电子浓度随r变化;Nm是单层电离层的最大电子浓度;qm代表分层厚度;地球半径为r0,则地心距离电离层的高度为rm,假设电离层到地面的高度为hm,则满足关系rm=hm+r0,rb是电离层的底端到地心的高度,则rb=rm−qm.为了方便模型的描述,采用分层的等离子体频率来描述电离层剖面模型.分层等离子体频率其中C0是常值80.6,电离层每层的截止频率(有时也称作临界频率)等于该层的最大等离子频率.由此,可以得到单层电离层的截止频率为它表示单层电离层最高位置的等离子体频率.
为了建立包含Es层的电离层模型,按照空间位置由下至上将电离层建模为8层,分别为Es层、Es_j1层、Es_j2层、E层、E-F1_j层、F1层、F1-F2_j层、F2层,其中Es_j1层和Es_j2层是Es层和E层之间的过渡连接层,E-F1_j层是E层和F1层之间的过渡连接层,F1-F2_j层是F1层和F2层之间的过渡连接层.不难发现,E层和F1层之间以及F1层和F2层之间都只用了一个过渡层进行连接,而Es层和E层之间却用了两段过渡层进行连接.其主要原因是:1)Es层的截止频率高于E层,所以两层之间存在明显的“脱节”,而且该“脱节”的规律是脱节处由大值陡降为小值,只用一层反转抛物线无法实现平滑连接;2)若只用一层反转抛物线,则连接段所占用的高度区间很大,而连接段的等离子频率均大于与其相接的E层连接点的等离子频率,这样相当于使Es层的厚度明显加大,与实际Es层厚度(1—2 km)不相符.电离层模型的上4层按照文献[6]进行建模,接下来主要给出下4层(Es层、Es_j1层、Es_j2层和E层)的建立过程.
Es层、Es_j1层、Es_j2层和E层的等离子体频率变化为:
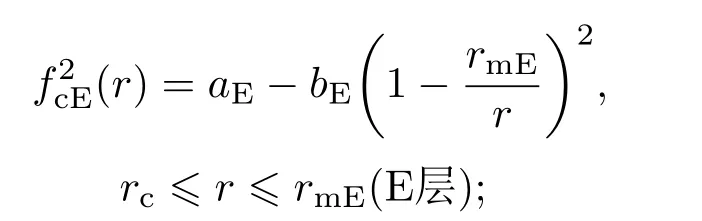
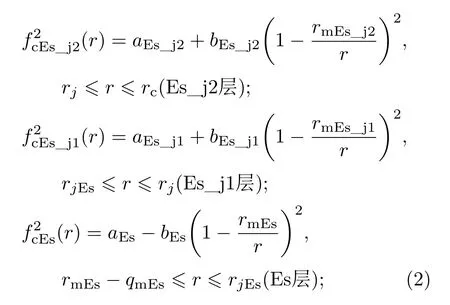
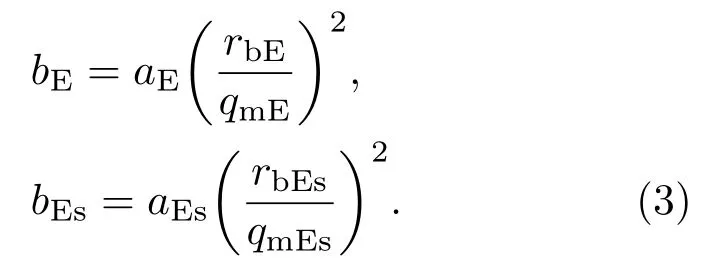
(2)式和(3)式中的参数含义分别为:rmE,rmEs分别表示E层和Es层的高度;rmEs_j1,rmEs_j2和rj均表示两个过渡层之间的连接点高度,则有rj=rmEs_j1=rmEs_j2;rc是Es_j2层和E层的连接高度;rjEs是Es_j1层和Es层的连接高度,qmE,qmEs分别是E层和Es层的层厚度,rbE,rbEs分别是E层和Es层的底层高度.这4层的简易空间位置关系见图2.
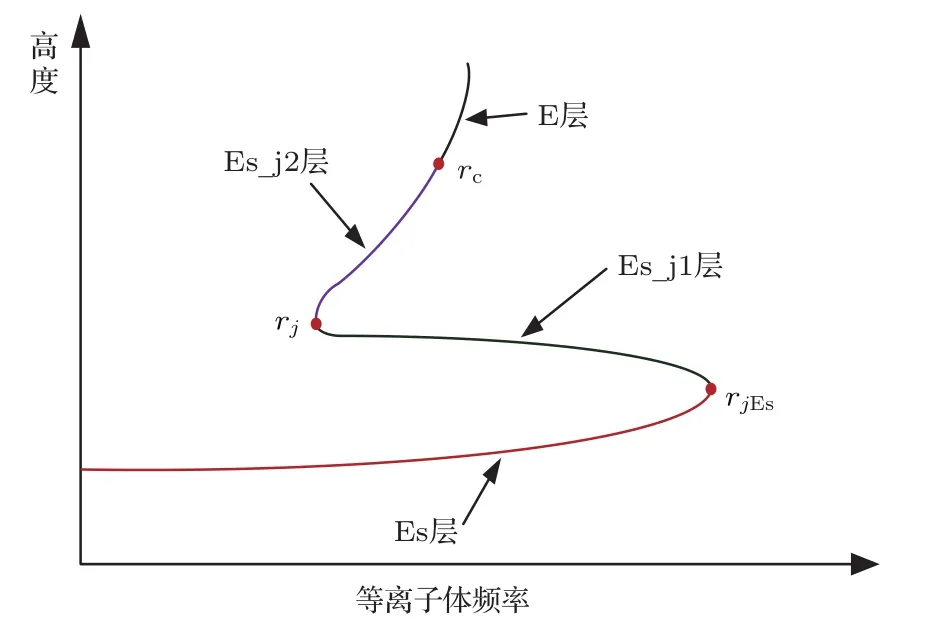
图2 电离层下4层的空间位置关系Fig.2.Spatial position relationship of the lower four layers of the ionosphere.
从(2)式和(3)式可以看出,有几个未知参数需要确定,即rc,rj,rjEs,aEs_j1,aEs_j2,bEs_j1和
bEs_j2.因为aEs_j1和aEs_j2分别表示两个过渡层的截止频率,为保证两个过渡层的反转连接,设置二者的关系为aEs_j1=aEs_j2[18],为了方便后文描述,令它们等于aj,参考实测数据,设置aj=0.3aEs;参考文献[18]的分析,Es_j1层和Es层的连接高度rjEs=rmEs+0.9qmEs.为了保证4个分层的连接处能够平滑过渡,需要满足两个基本条件:一是连接点处的导数值必须相等,二是连接点处的等离子频率(或者电子浓度)必须相等.以E层和Es_j2层为例,它们的等离子频率关于高度的导数表达式为:

根据基本条件一,连接点处的导数应相等,令以上两个导数等式相等,由于rmEs_j2=rj且r=rc(连接点高度),解方程可得bEs_j2:
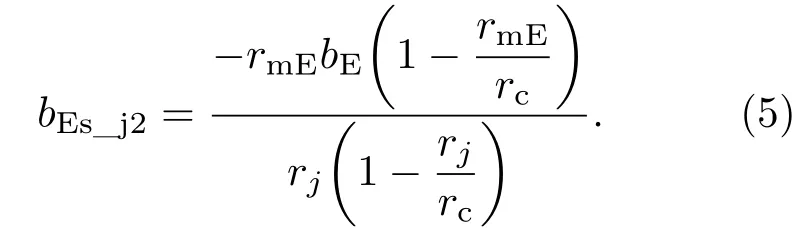
同理,可求得bEs_j1:
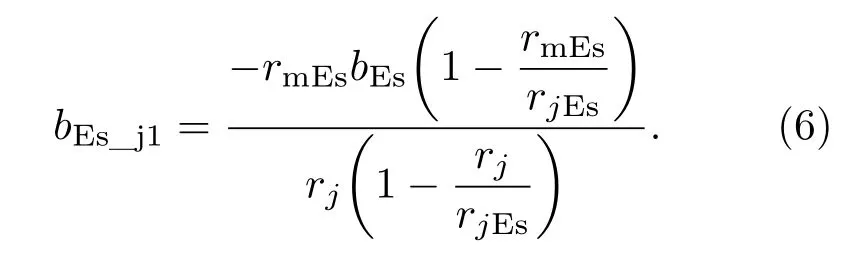
根据基本条件二,连接点处的等离子频率应相等,同样以E层和Es_j2层的连接点为例,根据(2)式,E层和Es_j2层在连接点rc高度的等离子频率应相等,则有
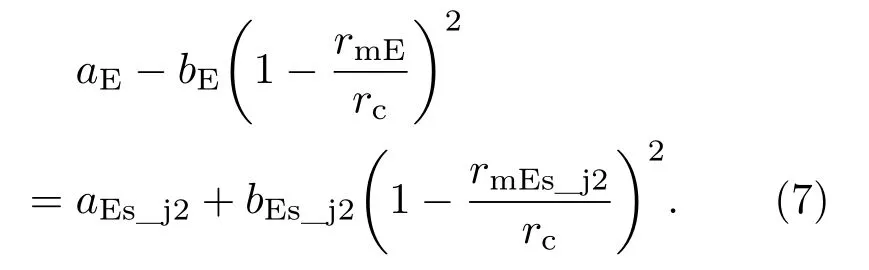
由于aEs_j2=aj,rmEs_j2=rj,且bEs_j2已经由(5)式计算出,所以解(7)式中的等式,可得到rc:
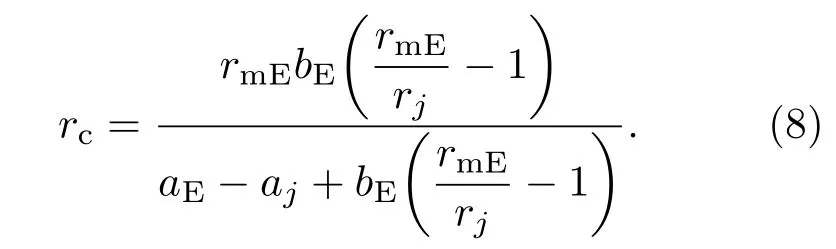
同理,可求得rj:
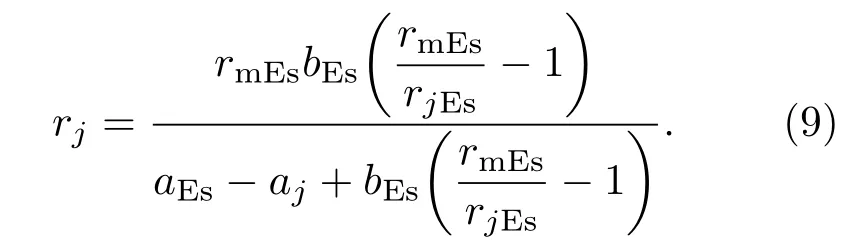
至此,电离层模型下4层的等离子体频率表达式的所有参数均全部解出,加上上面4层(E-F1_j层、F1层、F1-F2_j层和F2层),含Es层的电离层模型建立完毕.
2.3 基于实测数据分析的电离层参数选择与模型比较
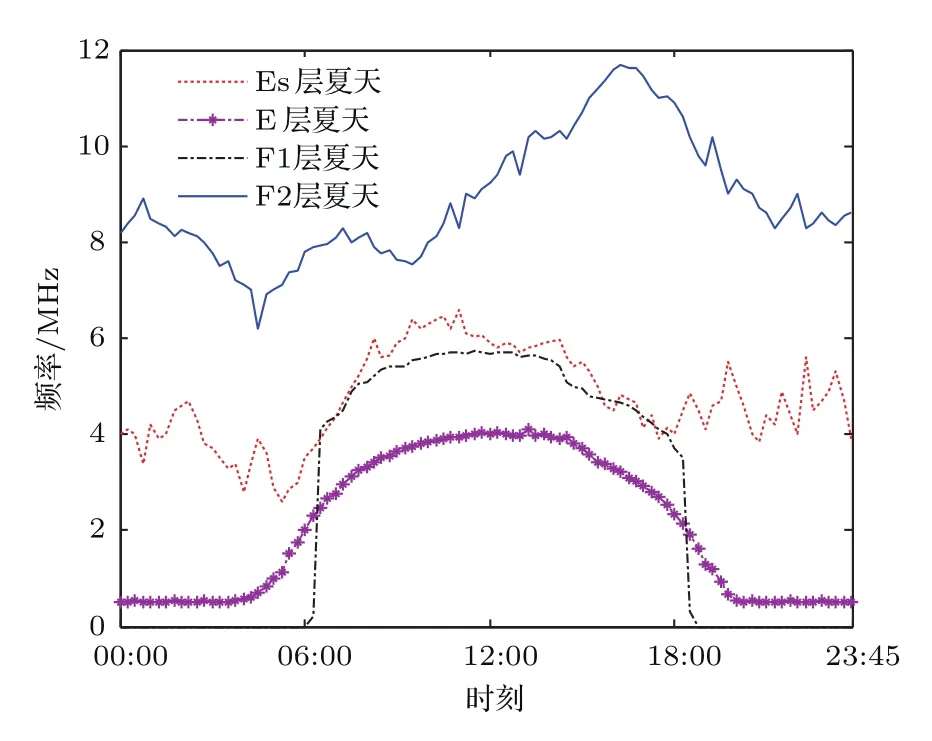
图3 电离层各层夏季的截止频率Fig.3.Cut-of ffrequency of each layer in the ionosphere in summer.
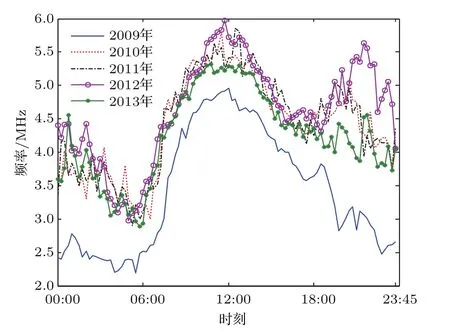
图4 Es层五年夏天截止频率Fig.4.Cut-o fffrequency of Es layer in summer for fi ve years.
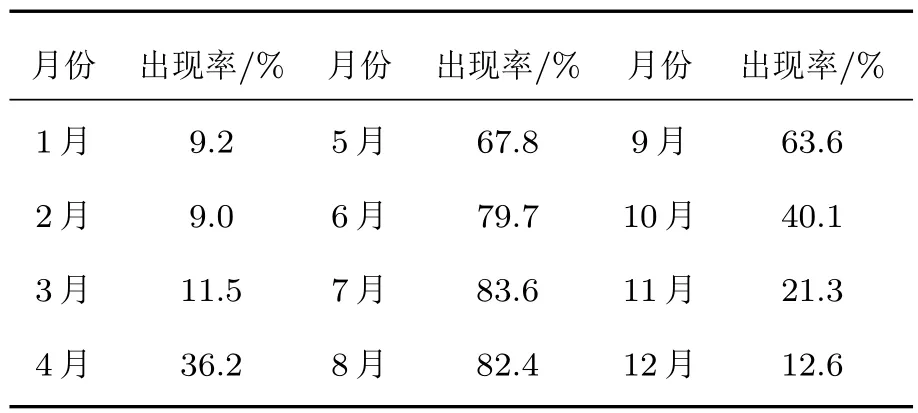
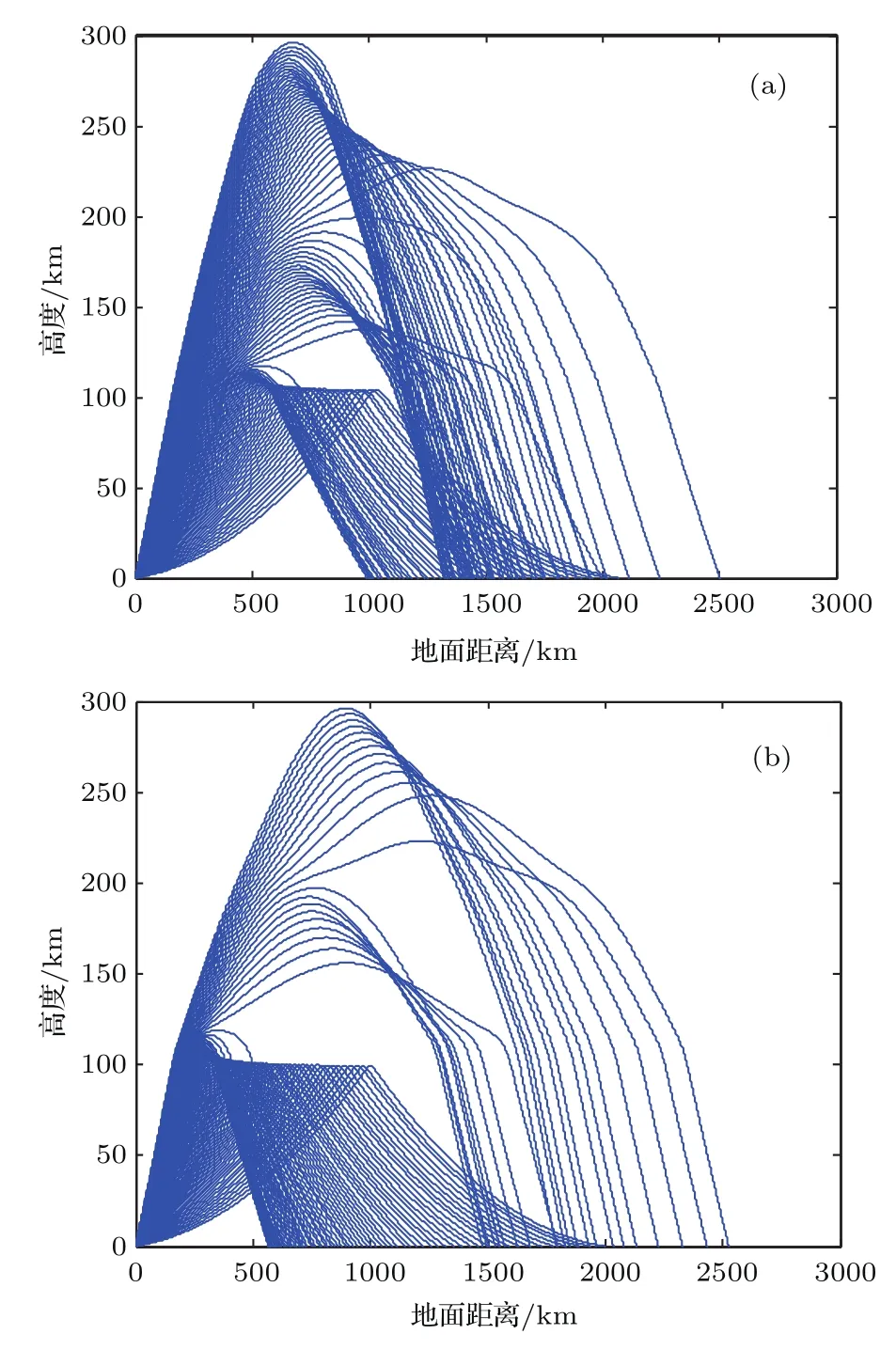
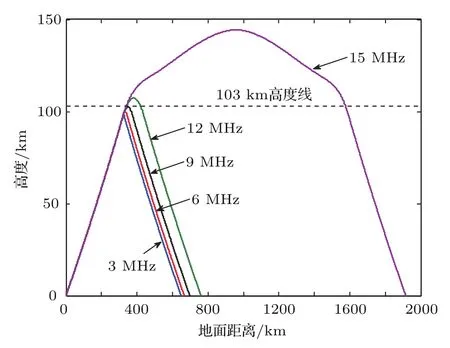
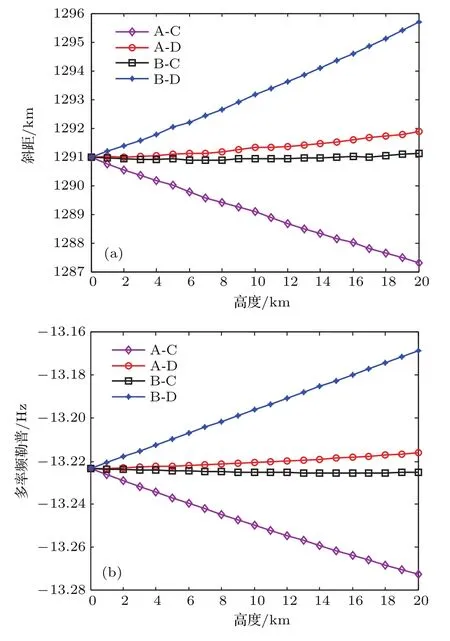
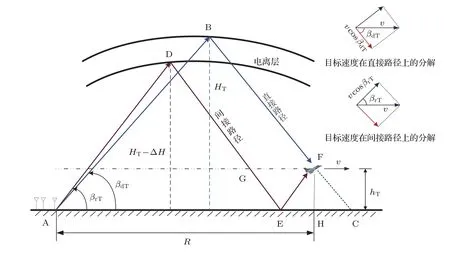
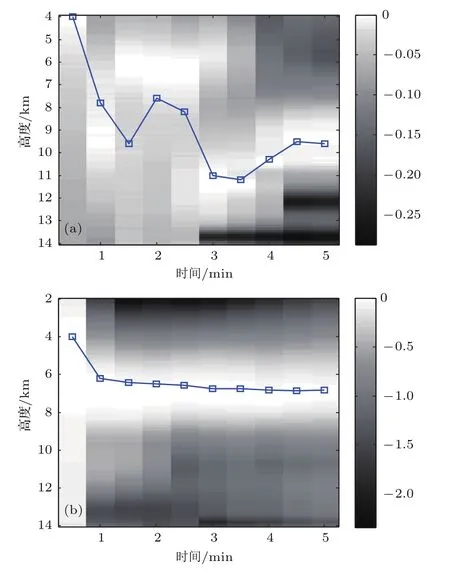
由于在建立电离层模型的过程中需要知道每个分层的截止频率,首先应该对电离层实测数据进行统计分析,获得电离层分层截止频率的范围值.数据仍然来源于某型天波超视距雷达配备的电离层垂测站的实测数据,图3是2013年夏季Es层、E层、F1层和F2层截止频率的全天平均变化情况,图4是2009年—2013年5年间Es层截止频率的全天平均变化情况,需要说明的是,图4中是以出现Es层的时间段进行计算的,没有出现Es层的时间段不参与平均值计算.从图3可以看出,夏季各层的截止频率的大小关系大致为fcE 为了与其他模型进行比较,将文献[12]中使用的不含连接层的三层电离层模型称作模型1,将文献[6]中使用的含连接层的三层电离层模型称作模型2,将本文建立的含Es层的电离层模型称作模型3.电离层参数设置为:参考实测数据,Es,E,F1和F2的截止频率分别为4.2,3.0,4.3和6.1 MHz;Es,E,F1和F2的层厚分别为1,20,87和100 km;Es,E,F1和F2的层高(相对于地面)分别为99.5,120,209.7和320 km.图5(a)—(c)是采用3种电离层模型计算的等离子频率随高度变化的电离层剖面曲线,图5(d)是三种模型的局部放大图,可见:模型1只建立了E,F1和F2三层模型,层与层之间没有加入连接层,导致等离子体频率变化不连续,出现了“断层”现象;模型2在E,F1和F2三层模型之间加入了2个连接层,保证了等离子体频率平滑连续,但该模型没有考虑Es层突发的情况;模型3在模型2的基础上加入了Es层和两个过渡连接层,在高度为99.5 km时Es层的等离子频率为4.2 MHz,达到了该层的截止频率,Es层从98.5 km的高度开始发展,形成的“电子云”薄层厚度为1 km,模拟结果与Arecibo非相干散射雷达在北纬18◦、西经67◦所测得的突发E层的实际电子密度剖面图[19]以及与2008年中国在挪威采用非相干散射雷达得到的电离层电子密度结果[20]是一致的,说明含Es层的电离层模型是合理可用的. 图5 三种电离层模型截止频率随高度的变化曲线 (a)模型1;(b)模型2;(c)模型3;(d)局部放大图Fig.5.Variation of cut-of ffrequency with height in three ionospheric models:(a)Model 1;(b)model 2;(c)model 3;(d)magnif i cation of Es layer. 表1给出了2010年全年的Es层截止频率大于4.5 MHz的出现率,从表中可以看出,Es层不是每天出现,但其具有很强的季节性,在夏季出现的概率远大于春、秋、冬季,所以在建立电离层模型时应该考虑季节性因素,避免发生模型失配.在具体实施中应根据两种情况进行处理:第一种情况,若能实时获取电离层垂测系统的测量结果,则可根据Es层是否出现,建立相应的电离层理论模型;第二种情况,若无法实时获取电离层垂测数据,则可根据历史统计结果建立电离层模型,一般的,在5—9月优先将电离层建立为含Es的模型,在其他月份优先将电离层建立为不含Es的模型,当然这种根据统计概率进行模型选择的方法的效果是低于第一种情况的,在应用中还应根据实际进行调整. 表1 2010年Es截止频率大于4.5 MHz的出现率Table 1.Probability of the cut-of ffrequency of Es is greater than 4.5 MHz in 2010. 在2.2节已经建立了含Es层的电离层模型,得到了电离层等离子体频率(电子浓度)随高度的变化表达式,利用每层的数学模拟公式可以获得高频射线到达地/海面(或者空中目标)时所对应的地面距离R、时延τ与高频射线的发射仰角β之间的关系.在不考虑地球磁场的条件下,电离层折射系数为 其中,fR是高频射线的频率.假设空中目标的高度为rt,则从高频射线发射设备到目标的地面距离可由下式计算[6]: 相对应的时延是 其中c表示光速,rM是射线能够到达的电离层最高点高度.利用QPS模型计算高频射线路径的主要过程是(以本文的含Es层模型为例):高频射线以β仰角进行斜向上发射,首先判断射线从自由空间进入Es层后是否能够穿透Es层,若高频射线未能从Es层穿过,说明射线在Es层发生了折射和反射,应求出射线在Es层的反射点高度(即rM),并采用(11)式和(12)式分别计算出地面距离和时间延迟;若高频射线从Es层穿透了,则继续判断射线进入Es_j1层后是否穿透,后续层(Es_j2,E,E-F1_j,F1,F1-F2_j和F2层)穿透与否的判断流程和前面的操作相同.由于采用QPS模型计算高频射线路径的公式和过程比较繁琐,这里不解释,具体的计算推导过程可参考文献[6].需要说明的是,本文采用的是解析式射线追踪+基于QPS的含Es电离层模型进行模拟计算的,与目前的数字式追踪法或者解析式追踪法(三段QPS模型)的区别在于依赖的电离层模型不相同. 为了分析不同电离层模型在计算高频射线传播路径时的差异,下面重点对电离层模型2和模型3的射线路径进行仿真分析.电离层参数和2.3节的参数设置相同,β取值范围为5◦—35◦,高频射线的发射频率为10 MHz,图6(a)和图6(b)分别是基于模型2和模型3计算的射线传播路径.从图6可得以下结论:1)模型2中的射线集中在E,F1和F2层上反射,模型3中的射线在Es,E,F1和F2层上均有反射,但模型2没有考虑Es层,使得本应该在Es层反射的射线到了E层才反射,另外,射线仰角越大,穿透到高层电离层的概率越大;2)模型3中的Es层截止频率大于E层,由于Es很薄,虽然多数仰角的射线均能穿透Es,但经过Es折射后,大部分都在E层高度范围内产生了反射;3)由于Es层的存在,扩大了高频射线的中近程探测的距离范围,模型2中射线能够探测到的最近地面距离是1000 km,即0—1000 km范围内是探测盲区,而模型3中射线能够探测到的最近地面距离是550 km,减小了中近程探测盲区,这同时也说明可以利用Es层进行中近程通信和探测工作. 图6 两种电离层模型计算的射线传播路径 (a)模型2;(b)模型3Fig.6.Ray Propagation path calculated by two ionospheric models:(a)Model 2;(b)model 3. 图7 射线频率和是否穿透Es层的关系Fig.7.Relationship between ray frequency and penetrating Es or not. 为进一步分析射线频率与射线是否穿透Es层的关系,设定发射仰角固定不变(20◦),高频射线频率分别为3,6,9,12和15 MHz,采用本文电离层模型3计算的射线传播路径如图7所示.从图7可以得到以下结论:1)在发射仰角固定时,射线频率越高,射线穿透Es层的可能性越大,3 MHz的射线在Es发生反射,6 MHz的射线刚刚穿透Es即发生反射,射线频率越高,探测距离也越远;2)当射线频率为9 MHz时,射线完全穿透了Es,图7中的103 km高度线即是9 MHz射线的反射高度,该高度已属E层区域;3)结合图6(b),由于Es很薄,多数的射线均能够穿透Es,但大部分都在E层被反射,其原因是发射仰角较小,高频射线在Es层发生折射后其入射角变得更小,即使穿透了Es,由于入射角变小且能量被削弱,故大部分在99.6—120 km(E层高度)的范围内发生了反射. 在第2节中,对QPS模型进行了完善,增加了Es层及其过渡连接段,利用这个模型就可以研究Es层突发情况下的测高模型和方法.由于电离层出现Es时会影响高频射线在电离层的反射点位置,而反射点高度决定了高频射线的传播路径,进而影响对目标高度的测量结果,所以,本节重点讨论基于高频射线微多径传播的测高理论,这是测高方法的理论基础. 假设高频射线的发射设备是天波超视距雷达,该雷达在远程早期预警中有着非常重要的作用,特别是能探测到弹道导弹等具有重大威胁的目标[21].高频射线发射后经电离层反射有两条路径到达目标,一条是直接发射路径(如图8中的实线A),一条是经海面反射后再到达目标的间接发射路径(如图8中的实线B);同样,目标反射回的射线也有两条路径到达接收天线,一条是直接返回路径(如图8中的虚线C),一条是目标反射到海面再经电离层反射回天线的间接返回路径(如图8中的虚线D).这样,发射和返回各有2条路径,则两两组合共有4条射线路径,分别是:直接发射-直接返回(A-C),直接发射-间接返回(A-D),间接发射-间接返回(B-D),间接发射-直接返回(B-C). 下面对高频射线的微多径模型进行仿真,参数设置为:电离层参数和高频射线频率与前文相同,目标与接收天线的距离为1200 km,目标水平向的飞行速度为−200 m/s,图9给出了目标高度变化时,4条高频射线微多径的变化情况.图9(a)所示为目标高度与微多径斜距的关系,图9(b)所示为目标高度与微多径多普勒频率的关系.可见,当目标高度为0 km时(即处于地面),4条路径是重合的,随着目标高度的增加,4条路径之间的斜距和多普勒频率也是呈增加趋势,但即使在高度为20 km时,4条微多径路径的斜距差异和多普勒频率差异均很小,这对于天波雷达是无法分辨的.但在确定电离层参数和射线传输模式下,时延和地面距离与目标的高度有对应关系,这样就可以惟一确定4条多径路径的多普勒频率和斜距,从而为测高提供了理论依据. 图8 高频射线的微多径反射模型Fig.8.Micro-multipath reflection model of high frequency rays. 图9 目标高度与微多径的关系 (a)高度与微多径斜距的关系;(b)高度与微多径多普勒频率的关系Fig.9.Relationship between target height and micromultipath:(a)Relationship between height and micromultipath slant range;(b)relationship between altitude and micro-multipath Doppler frequency. 图10给出了微多径与目标和电离层之间的几何关系示意图(以发射多径为例进行说明).其中的符号含义为:βdT和βrT分别是射线直接发射和间接发射的仰角,R是地面距离,v是目标水平速度;A,B,D,E和F点分别代表发射天线位置、直接路径电离层反射点、间接路径电离层反射点、间接路径海/地面反射点和目标所在位置;HT,hT和∆H分别代表电离层B点距地面的高度、目标高度以及电离层B点和D点的高度差. 通过对△ADE,△ABC,△FEC,△FHC和△FEG这几个三角形的几何关系进行联合计算,可得直接路径的斜距和仰角 同理,可得间接路径的斜距和仰角 图10的右上角是将目标的水平速度分解到直接路径和间接路径方向上的示意图,由此可得直接路径的多普勒频率为fdT=2vcosβdT/λ,间接路径的多普勒频率为frT=2vcosβrT/λ,λ是高频射线的波长.以上是两条发射多径路径的斜距和发射仰角的推导.同理,两条接收多径的斜距和接收仰角也能够推导出.可以看出,微多径的斜距和多普勒频率与目标的高度、地面距离以及电离层的反射点高度有关,电离层反射点又与电离层参数相关.有了这个结论,通过建立适当的电离层模型,利用微多径射线传输特性可以模拟出多径回波并结合相应测高算法,就可以估计出目标的高度. 图10 微多径的几何模型Fig.10.Geometric model of micro-multipath. 对于雷达探测设备,目标的地面距离是已知量,利用2.4节中射线仰角与地面距离的关系式并结合电离层模型,可以计算出全部多径射线的4个仰角;同时,根据时延与射线仰角的关系,计算出4条多径射线的时延;利用3.2节中目标在多径斜距上的速度分解,可以计算出4条多径射线的多普勒频率.这样,根据4条多径射线的多普勒频率和斜距(通过时延计算),就能够模拟出目标的4条多径回波信号.将模拟仿真出的4条多径回波与实际天波雷达的接收回波进行相关计算,则相关函数达到最大值时所对应的高度就是估计出的目标高度,这就是匹配域测高的基本原理.从测高原理可以看出,建立合理且正确的电离层模型是模拟出4条多径射线的前提,若电离层模型错误,则后续的测高工作无法有效开展. 在匹配域测高原理的基础上,文献[11]提出最大似然估计的高度测量方法,将探测回波的第k个扫描周期数据写成矩阵的形式: 该式是利用距离-多普勒进行表示的,其中Hk矩阵的大小是NM×4,N和M分别是回波多普勒维和距离维的数据点数,Hk的第l列为hk,l=al[k]⊗ bl[k],l=1,………,4,al[k]和bl[k]是目标在距离-多普勒二维面上的距离维和多普勒维数据,⊗是Kronecker积运算,则Hk的一列就对应一条多径数据;θk是随机的回波相位;Dk是维数为4的对角矩阵,[Dk]l,l=exp(jωl,k tk),tk是驻留周期,ωl,k是多普勒频率,与目标高度相关;ck是多径回波幅度,其符合一阶Markov模型;nk是高斯白噪声.(15)式中,Hk和Dk包含了射线电离层反射点位置和目标高度的信息. 将多次扫描回波数据和模拟多径数据进行联合处理,建立目标高度的联合概率密度函数并求解其对数似然函数,函数最大值对应的高度就是估计解[11], 其中,xk是第k个扫描周期数据,h是待验证的目标高度,∆θk=θk −θk−1.通过遍历h的取值范围,当(16)式达到最大值时,此时即得到高度估计值. 实际探测中,要求对目标高度能够快速、连续地测量,但是文献[11]需要利用(16)式对目标高度进行穷尽式遍历搜索,所以测高的时间大部分都消耗在搜索上,搜索步长越小则时间越长.爬山法[22]是一种经典的启发式搜索法,算法简单且搜索速度快,其原理是:目标函数的局部极大值就像一个个山峰,爬山法就是选择最有希望的道路到达最大值,即选择最“陡峭”的道路进行攀登,但是搜索初值对该方法有较大影响,要求落入“最高峰”的范围附近,而且该方法容易陷入局部山峰(局部极大值),最终导致估计的高度值并不是真正的目标高度.为克服这个缺点,采用先对目标高度进行粗估计,再采用分段的爬山搜索法进行精细搜索,能够较大地减少搜索时间.搜索的流程如下. 步骤1从(12)式可见,4条多径的时延τl(l=1,………,4)与目标的高度有很大关系,目标的高度越高,则4条多径的τl差别越大,这样在回波距离域的区别也就越明显.利用微多径的这个特性,首先采用距离域高分辨法[23]估计出目标高度的大致范围,其基本原理是:目标多径回波在距离域的扩展程度与高度相关,利用高分辨技术对扩展的多径距离域信号进行识别,根据距离维的多径个数可以判断目标位于哪个高度范围内,该方法只能初步将目标定位为3个高度范围:低高(0—4 km)、中高(4—12 km)和超高(12 km以上). 步骤2经过步骤1的粗估计后,已经确定了目标高度处于某个高度范围,则h∈[hd,hu],其中hu和hd分别表示该高度范围的最高端和最低端.将该高度范围平均划分为s个子段,这样划分有两个好处:一是即使目标函数存在多个“山峰”,通过分段后,每个“山峰”均落入各自的搜索区间,能够防止搜索收敛到局部极值;二是经过分段细化后,即使搜索初值随机选择,也能保证其落在“山峰”附近.根据(16)式,第i段的目标函数为 其中i=1,2,………,s,hui和hdi限定了第i段的高度区间,对每个区间都采用爬山法进行搜索,并记下每段搜索出的目标函数最大值gimax. 步骤3比较s个子段的gimax,设其中的最大值为gmax,则gmax所对应的高度即为估计出的目标高度值. 可以看出,通过粗估计加分段精细搜索的组合方法,能够避免搜索不必要的高度区间,同时也能避免爬山搜索法收敛到局部极值,真正“攀登”到实际高度.下面对两种搜索方式的时间消耗进行比较,电离层参数与前文相同,高频发射机工作频率为10 MHz,带宽20 kHz,目标飞行高度7 km,水平向速度为200 m/s,相干积累时间2.5 s,信噪比20 dB,表2是一次重访数据平均搜索时间的比较结果.由表2可见,粗估计加分段爬山的组合搜索能够大大节省搜索时间,其时间消耗只有全局穷尽式搜索的十分之一. 表2 一次重访数据的平均搜索时间Table 2.Average search time for one revisited data. 图11 不同电离层模型的测高结果 (a)模型2的测高结果;(b)模型3的测高结果Fig.11.Results of height estimation using different ionospheric models:(a)Model 2;(b)model 3. 仿真参数不变,高频射线重访间隔30 s,进行10次重访(5 min),分别采用电离层模型2和电离层模型3,利用分段爬山搜索的快速匹配域方法进行目标高度计算,结果如图11所示.其中图11(a)和图11(b)分别是采用模型2和模型3的估计结果,灰度图中的每一列对应一次重访数据的高度似然估计值,颜色越浅表示似然函数值越大(将每次重访数据的最大似然值归一化为0 dB),图中曲线点“?”代表每次重访估计的最大似然值对应的高度.图11表明,基于电离层模型3的测高结果与实际高度很接近,从第3次重访数据加入开始,其估计误差就小于0.4 km;而采用模型2的测高结果误差很大,即使10次重访数据全部使用完,误差也达到2.6 km,其主要原因是模型失配导致模拟多径射线的延时和多普勒频率均发生错误,最终无法与扫描回波数据实现真正的匹配. 电离层具有明显的分层结构,其各分层具有不同的截止频率,高频射线根据射线仰角的不同,会在不同的分层发生折射和反射.由于突发的Es层无法忽略,目前高频射线测高研究中的电离层模型均未考虑Es层,当Es层出现时,测高模型将失效.本文在QPS模型的基础上,研究了含Es层的电离层模型,并结合该模型给出了分段爬山搜索的快速匹配域测高方法,主要的结论有: 1)根据电离层垂测站的实测数据统计分析,发现在北半球的中纬度地区,出现Es层的概率很大,特别在夏季,昼夜均能突发形成,Es层的截止频率明显大于与其临近的E层,甚至与F1层的截止频率相当; 2)由于Es层的截止频率大于E层,相同发射仰角下的高频射线,原本应该被E层(或F1层)反射,在Es层突发时,射线会在进入E层前被Es层先反射,结果是减小了高频射线中近程的探测盲区,探测区域约增大了500 km; 3)高频探测射线具有一定的波束宽度,使得从目标反射回来的射线路径不止一条,通过对多条路径的微多径特征进行仿真分析,说明能够利用各路径的时延和多普勒频率差异对回波信号进行模拟,采用模拟的多路径回波数据与实际回波数据进行匹配处理,能够实现目标高度测量; 4)给出的先进行高度粗估计再分段精细搜索的方法,在保证结果准确度的前提下,能够使高度搜索时间减小到全局搜索的十分之一,大大提高了搜索效率. 需要指出的是,当受到地震、磁暴等外界因素影响时,电离层电子密度会出现异常变化,电离层模型需要进行修改;同时,由于缺乏确切已知目标高度的实测数据,文中仅用了仿真数据进行验证,这些方面在今后的研究中均需要进行补充完善. [1]Forbes J M,Palo S E,Zhang X 2000J.Atmosph.Solar-Terr.Phys.62 685 [2]Šauli P,Bourdillon A 2008J.Atmosph.Solar-Terr.Phys.70 1904 [3]Han Y M,Hu J,Kong Q Y,Fan J M 2009Chin.J.Radio Sci.24 929(in Chinese)[韩彦明,胡进,孔庆颜,凡俊梅2009电波科学学报24 929] [4]Hao S J,Zhang W C,Zhang Y B,Yang J T,Ma G L 2017Acta Phys.Sin.66 119401(in Chinese)[郝书吉,张文超,张雅彬,杨巨涛,马广林2017物理学报66 119401] [5]Croft T A,Hoogasian H 1968Radio Sci.3 69 [6]Dyson P L,Bennett J A 1988J.Atmosph.Solar-Terr.Phys.50 251 [7]Norman R J 1997Radio Sci.32 397 [8]Bilitza D 2001Radio Sci.36 261 [9]Reinisch B W,Huang X Q 2000Adv.Space Res.25 81 [10]Scotto C 2009Adv.Space Res.44 756 [11]Papazoglou M,Krolik J L 1999IEEE Trans.Signal Process.47 966 [12]Papazoglou M 1998Ph.D.Dissertation(Durham:Duke University) [13]Smith L G,Mechtly E A 1972Radio Sci.7 367 [14]Whitehead J D 1961Nature20 49 [15]Whitehead J D 1989J.Atmosph.Solar-Terr.Phys.51 401 [16]Nie M,Tang S R,Yang G,Zhang M L,Pei C X 2017Acta Phys.Sin.66 070302(in Chinese)[聂敏,唐守荣,杨光,张美玲,裴昌幸2017物理学报66 070302] [17]Sun L F,Zhao B Q,Yue X A,Mao T 2014Chin.J.Geophys.–CH.57 3625 [18]Norman R J,Dyson P L,Bennett J A 1998S-RAMP Proceedings of the AIP CongressAustralia,September,1998 p147 [19]Tan H 2004Ph.D.Dissertation(Wuhan:Wuhan Institute of Physics and Mathematics Chinese Academy of Sciences)(in Chinese)[谭辉 2004博士学位论文 (武汉:中国科学院武汉物理与数学研究所)] [20]Li H,Che H Q,Wu J,Wu J,Xu B 2011Chin.J.Radio Sci.26 311(in Chinese)[李辉,车海琴,吴健,吴军,徐彬2011电波科学学报26 311] [21]Wu X,Chen J W,Bao Z,Guo D Y 2014Acta Phys.Sin.63 119401(in Chinese)[吴瑕,陈建文,鲍拯,郭德阳2014物理学报63 119401] [22]Hinson J M,Staddon J E R 1983J.Exp.Anal.Behav.40 321 [23]Anderson C W,Green S D,Kingsley S P 1996IEE Proc.-Radar,Sonar Navig.143 281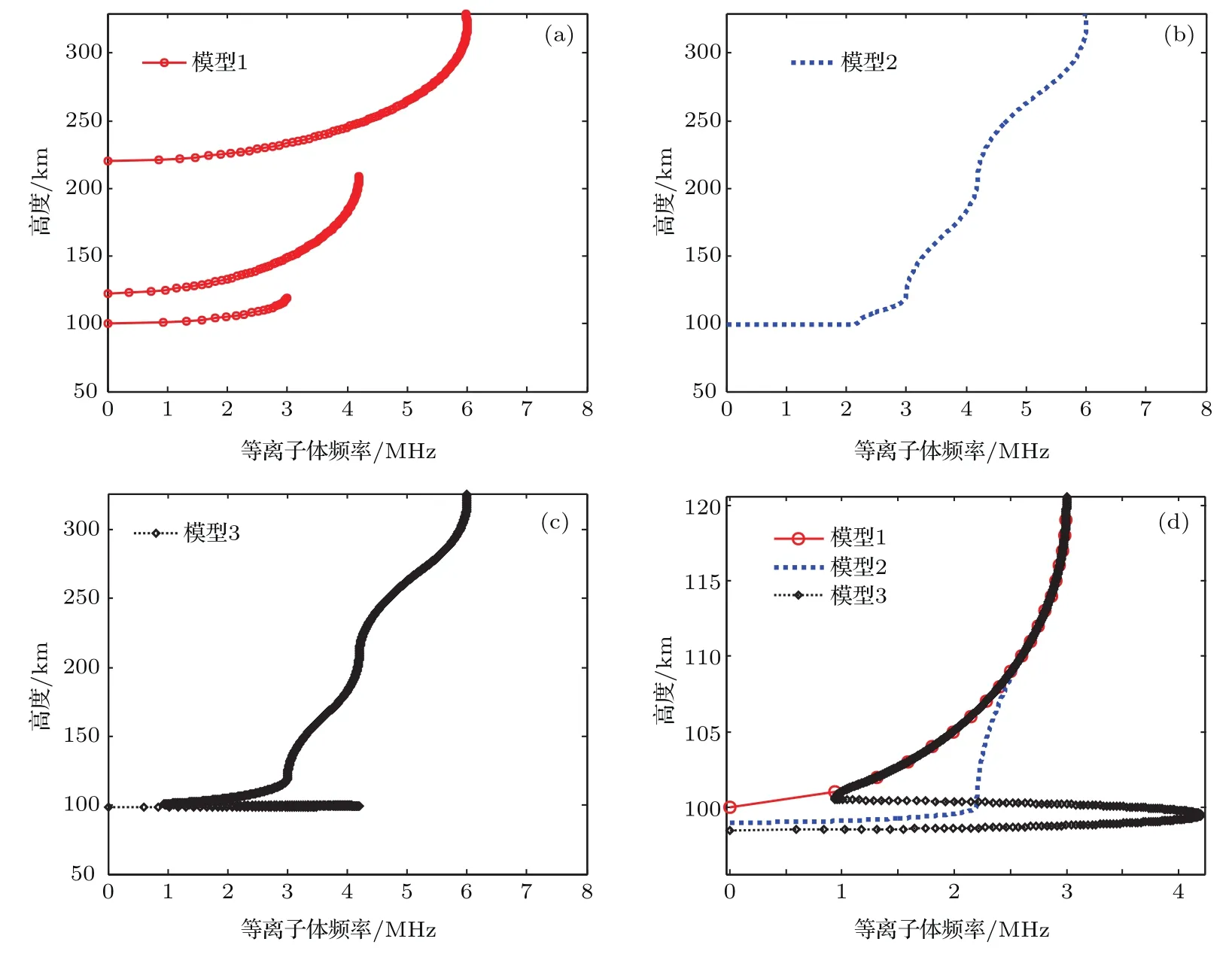
2.4 利用含Es层的电离层模型计算高频射线路径
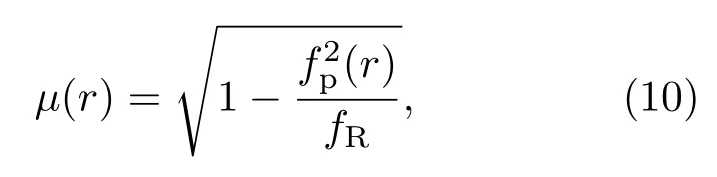
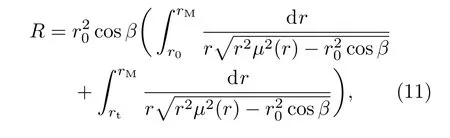
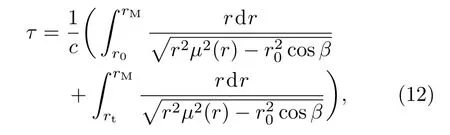
3 高频射线微多径传播与测高模型
3.1 高频射线的微多径模型
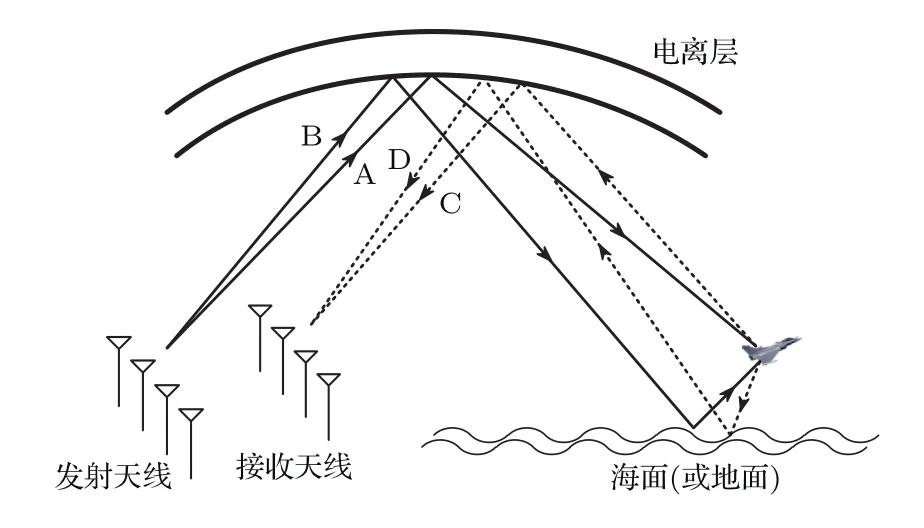
3.2 基于微多径的测高几何模型

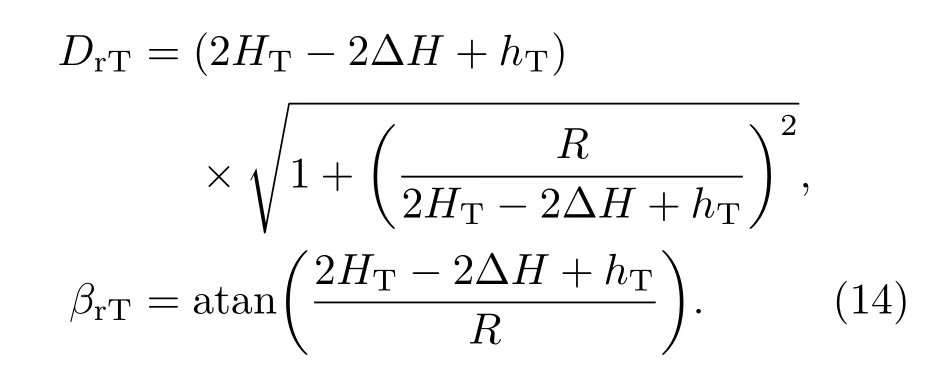
4 基于高频射线微多径的测高方法
4.1 最大似然估计方法
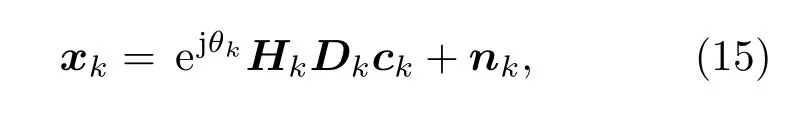
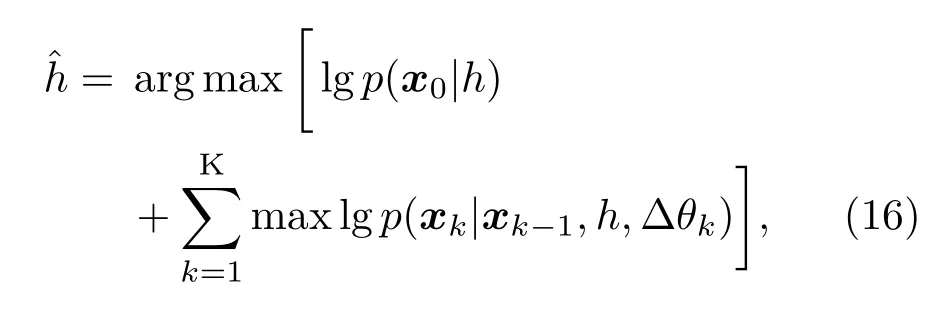
4.2 分段爬山搜索的快速匹配域方法


5 讨论与结论

