窗口声阻抗对锆相变动力学的影响∗

种涛王桂吉谭福利赵剑衡唐志平

1)(中国工程物理研究院流体物理研究所,绵阳 621900)

2)(中国科学技术大学近代力学系,合肥 230027)

1 引 言

磁驱动斜波加载技术是一种可对材料进行平滑上升压缩的新型实验技术,每发实验对应热力学路径中的一条准等熵线.由热力学理论可知,等熵线介于等温线和Hugoniot线之间,因此,斜波加载技术是对准静态和冲击加载技术的补充,具有重要的科学价值.与冲击加载技术相比,斜波加载是一连续过程,应力-应变响应对材料响应的微小变化敏感,能够充分观测到波传播过程中的扰动(材料细微响应),因此斜波压缩技术在相变动力学研究中有明显的优势.

1945年,麻省理工学院的Kaufman和Pomerance发现锆的热中子吸收截面极低,还具有良好的导热、焊接及机械性能,抗核辐射损伤能力很强,在酸碱环境中耐腐蚀性很好,因此,锆是最佳的反应堆结构材料之一[1].另外,锆具有很强的吸氢能力,所以氢化锆是反应堆中优良的慢化剂.锆不仅在核工业中被大量应用,同时也具有很广阔的非核用途.如化工品制造业、医学领域,甚至制造超导体.随着金属锆及其合金在各个领域日益广泛的应用,人们对纯锆的力学性能研究也越来越多.1952年,Bridgman等[2]通过静压研究发现锆在5.9 GPa时出现波阻抗不连续,因此提出这是由于发生了相变.1963年,Jameison[3]通过X射线衍射实验验证了Bridgman实验中新相为ω相.Zilbershteyn等[4]做了锆的静水压压缩实验,发现其平衡相变压力为2 GPa.Xia等[5,6]通过实验发现32 GPa压力以上锆出现β相,且证明了在高温和高压下得到的β相是同一个相.Al’tshuler等[7,8]和McQueen等[9]提出了锆的冲击相变实验,它们发现锆的冲击波速度-粒子速度在26 GPa压力处出现拐点.Kutsar等[10]在实验中得到了锆的多波结构波剖面,通过理论分析指出锆在6.5 GPa左右发生了α-ω相变.2005年,Los Alamos国家实验室[11,12]对不同纯度的锆进行了冲击相变实验,结果表明三种纯度的锆在冲击压缩下相变起始压力不同,此外还发现氧含量对相变压力影响较大.文献[13]从原子结构角度分析了氧含量对冲击相变压力的影响.2009年,Greef f等[14]再次深入地研究了纯度对锆相变的影响,实验中对三种不同纯度的锆分别进行了冲击压缩和准等熵压缩,实验结果与2005年的实验相同:随着氧含量的增加,锆的α-ω相变初始压力提高.而准等熵压缩相变实验发现,氧含量仅影响锆的α-ω相变压力,而对于高压相变(ω-β)起始压力无影响.肖大武[1]利用SHPB装置对锆的本构关系进行了较系统的研究.李英华[15]利用轻气炮装置开展了锆的冲击压缩低压相变和层裂损伤研究.2013年,种涛等[16]基于磁驱动斜波压缩装置CQ-4,开展了不同加载压力和样品尺寸锆的斜波压缩低压相变实验研究.

目前锆的冲击相变实验和理论分析较多,而斜波压缩实验和相应的理论分析很少,本文利用CQ4装置[17]开展了相同加载条件下不同窗口纯锆的斜波压缩相变实验,研究样品后表面窗口特性对带有相变信息的速度波剖面的影响,并利用基于Helmholtz自由能的多相状态方程及非平衡相变速率模型对实验过程进行了数值模拟,计算结果与斜波压缩相变实验结果符合良好,可以较好地模拟锆的弹塑性转变、相变等物理过程.在压力-比容平面,锆的冲击绝热线与准等熵线在相变前差异很小,从相变起始点分离,进入新相后准等熵线在冲击绝热线下方.温度-压力相图中,相变前准等熵线与冲击绝热线差异很小,相变后准等熵线位于Hugoniot线下方,且随着压力的增加两条线偏差越来越大,在20 GPa两者相差约100 K.相变开始后,拉氏声速下降约7.1%,相变完成后又恢复到体波声速.

2 实验加载原理与负载区设计

2.1 磁驱动斜波加载实验原理

实验在磁驱动实验装置CQ-4[17]上进行,该装置主要由储能电容器、电流波形调节的峰化电容器、传输板和负载区等部分组成.当充电电压85 kV时该装置可在负载区输出上升沿约500 ns、峰值约4.2 MA的光滑脉冲电流.当脉冲电流经过平行的U形负载区电极回路时,会在上下电极之间产生强磁场,磁场再和导体中的电流相互作用产生洛伦兹力.由于电流的趋肤效应,该电流沿上下极板的内表面流过,因此形成的洛伦兹力即磁压力也形成于极板的内表面沿极板厚度方向传播,作用于置于极板上的实验样品.两极板内表面受到的磁压力[18]为

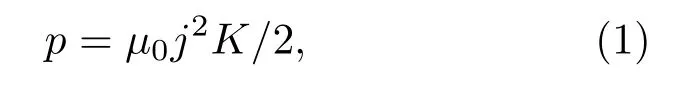
其中j为线电流密度,µ0为真空磁导率,K为实际磁压力与理论磁压力的比,它与极板构型、上下极板间隙和电极材料等相关.

2.2 实验负载区设计

磁驱动斜波加载实验负载区驱动电极和样品设计及尺寸确定,需满足样品一维应变加载,同时在样品中不能形成冲击波.具体的设计方法可参考文献[19].

本实验的负载区布局如图1(a)所示.单发实验四个速度测试点,分别为三个样品和一个极板自由面测速,测速点均在样品中心位置.利用任意反射面速度干涉仪(velocity interferometer system for any reflector,VISAR)进行速度测量.极板材料为铝,窗口分别为LiF和蓝宝石,具体实验条件见表1.为了验证实验电极的加载均匀性,首先进行了不带样品的极板自由面四点测速实验,结果见图1(b),在实验关注的时间段内,四点均匀性优于±1%,满足实验要求.

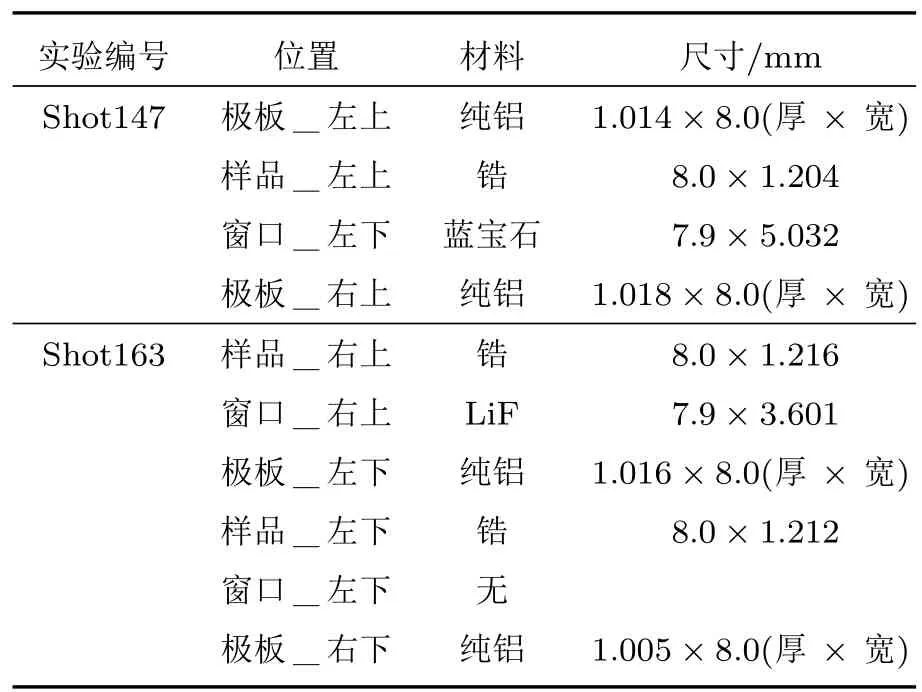
表1 实验条件Table 1.Experimental condition.

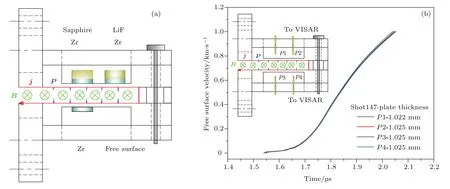
图1 实验负载区示意图及加载均匀性验证 (a)负载区示意图;(b)极板自由面速度Fig.1.Load area schematic and loading consistency results:(a)Loading area schematic;(b)free surface velocities.

3 实验结果

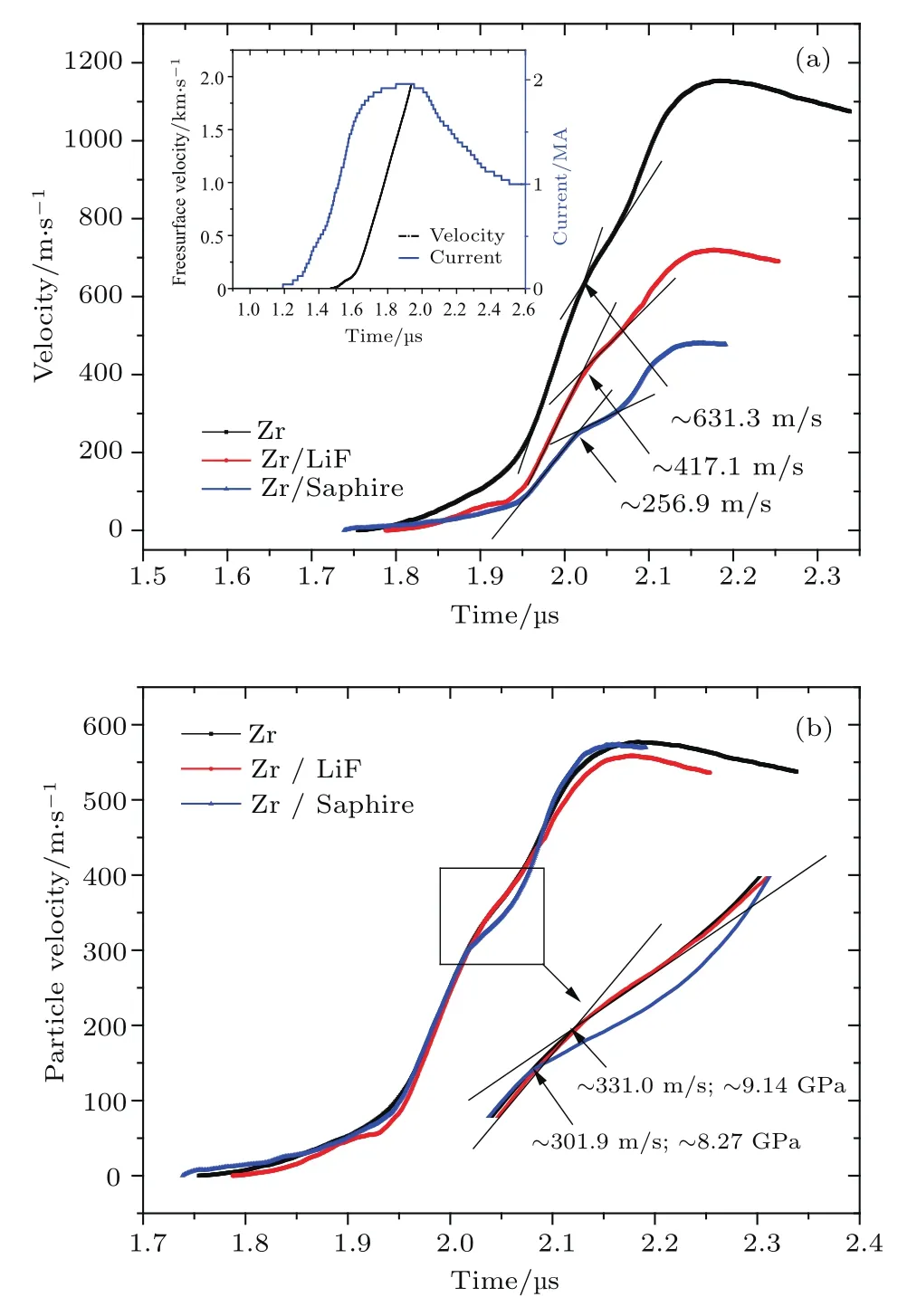
图2 shot163实验结果 (a)实验测量界面速度剖面;(b)粒子速度剖面Fig.2.Experimental results of shot 163:(a)Measured interface velocities;(b)particle velocities.

实验测量结果见图2.图2(a)为样品与窗口界面粒子速度和驱动电极板的自由面速度,图2(a)内插图为实验时装置放电电流曲线和极板自由面速度曲线.从图2(a)看到,加载电流平滑上升,其上升沿约600 ns,峰值约2.0 MA.极板内表面加载应力由极板后表面自由面速度历史结合反积分程序给出,其上升沿约500 ns,峰值约20 GPa.对比三个锆样品的后表面速度波剖面,其波形基本相似,随着加载压力的提高,速度平滑上升,波剖面均出现了相变波结构,加载至峰值压力后速度下降,各物理过程的时序基本一致,整个过程无冲击形成.由于样品后表面阻抗的差异,速度波形和相变压力存在一定差异.自由面和LiF窗口都属于样品后表面低阻抗情况,其速度波剖面相似,在相变对应的速度区间斜率相近;蓝宝石窗口与锆样品是高阻抗匹配,相变对应的速度区间斜率明显减小.利用阻抗匹配法将三种情况的界面速度转化为粒子速度,见图2(b).可以看到三种情况的速度波形基本一致,但是在相变对应的速度平台处波形存在差异,与上面的分析一致.自由面和LiF窗口低阻抗匹配条件下,锆样品相变起始对应的波剖面粒子速度约为331.0 m/s,而蓝宝石窗口高阻抗匹配情况下,锆样品相变起始对应的波剖面粒子速度约为301.9 m/s.锆样品后表面匹配低阻抗窗口(自由面和LiF)时,压缩应力波在后表面反射回稀疏波,锆样品后表面无法相变.蓝宝石窗口声阻抗大于锆样品,加载应力波在样品/窗口界面作用后,反射回压缩波,加载波与反射压缩波叠加,导致样品在界面一侧压力提高,使得锆样品在界面一侧发生相变,且更容易成核,成核密度较高.因此,较低的加载波在界面作用后,使样品达到相变条件,宏观上表现为相变开始时对应的粒子速度较低.相似结果在铁的斜波压缩实验中也有发现[16].由实验和理论分析可知,界面处的速度波形与样品动力学特性、窗口特性和加载条件等多种因素相关,因此,速度波剖面中相变起始对应的速度特征拐点是与多种因素相关的实验信息,不应该将其定义为材料属性参数相变压力.

4 数值模拟与分析

要准确描述包含相变的动力学过程,除了质量、动量和能量守恒方程之外,还需要描述相变过程的相变速率方程和考虑相变的多相状态方程.

相变速率方程采用郭扬波[20]在Hayes[21]基础上提出的模型,其物理背景为:相变速率与相变驱动力、可供其生长的空间成正比,1相向2相转变的演化方程为

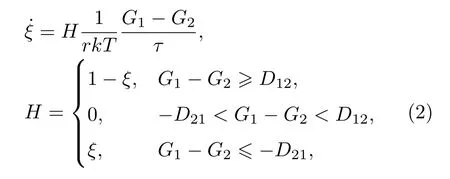
其中ξ为新相的质量分数,H为可供初始相相变的生长空间,G1−G2为相变驱动力,r为单位体积中的原子数,τ是相变弛豫时间(它决定相变建立平衡需要的时间),k为Boltzmann常数,T为当前温度,G为Gibbs自由能,D12为初始相向新相转变的能障,D21为新相向初始相转变的能障.

相变速率方程需要计算各相的Gibbs自由能,而Gibbs自由能也可以由Helmholtz自由能得到.锆在给定比容V和温度T时的Helmholtz自由能[22]为

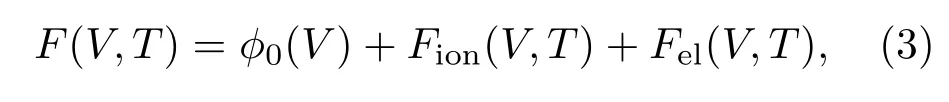
其中第一项为冷能,第二项为离子热振动自由能,第三项为电子热激发自由能,各相具体表达式如下:

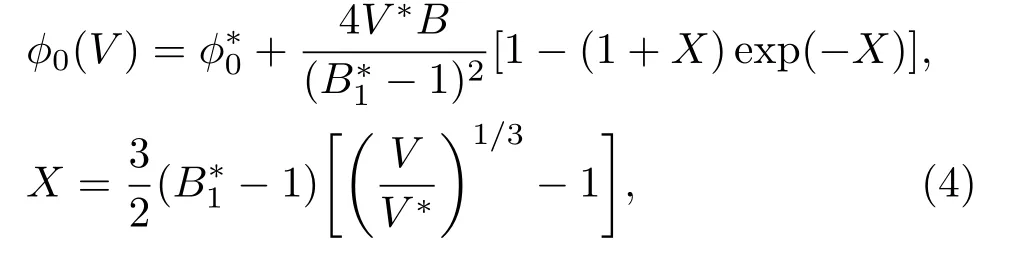
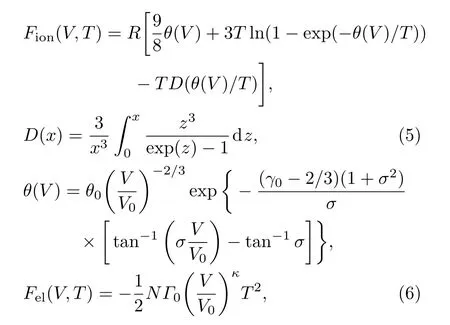
其中ϕ ∗0是在最低能量时的静态的晶格能,V ∗是最低能量时的比容,R是材料常数(锆为0.0911 J/(kg)),V0是参考比容,θ0和γ0是在参考比容V0时的θ(V)和Gruneisen系数,Γ0,κ和σ是模型参数,N是锆单位质量的原子数,B ∗和B ∗1分别是体模量及体模量对压力一阶偏导数的系数.锆的Helmholtz自由能参数见表2.

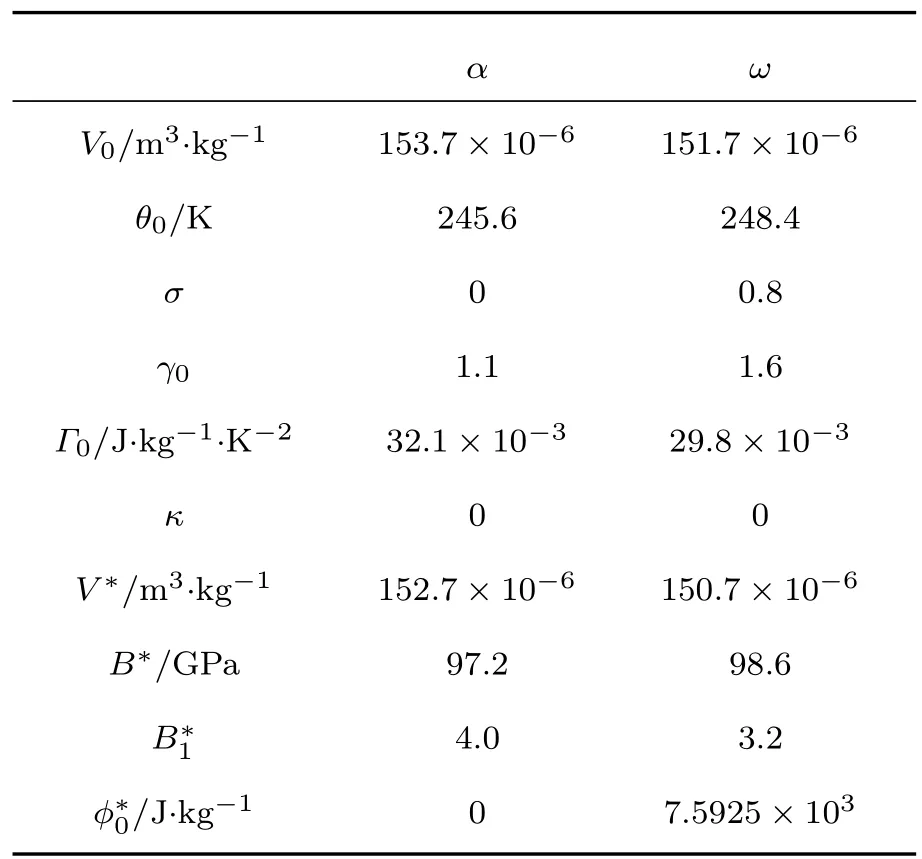
表2 锆的Helmholtz自由能计算参数[13]Table 2.Parameters of the Helmholtz free energy of zirconium.

由热力学关系可知,确定某系统的热力学完全状态方程后,该系统的所有热力学性质和热力学参数都可以被确定[20].热力学完全状态方程(或称热力学势函数)有4种:内能E(V,T),热焓H(V,T),Helmholtz自由能F(V,T)和Gibbs自由能G(V,T).因此,确定锆的两相Helmholtz自由能形式及相应参数后,可以得到对应状态下锆的压力、熵,内能和Gibbs自由能,见(7)式.联立(3)式到(7)式中的压力表达式,可得锆基于Helmholtz自由能的多相状态方程(F-MEOS),具体表达式如下:

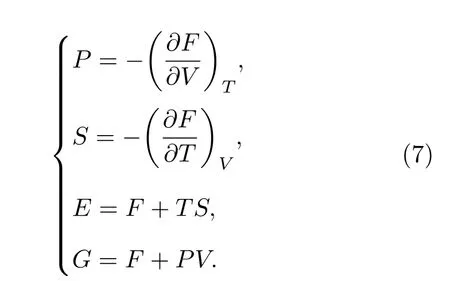
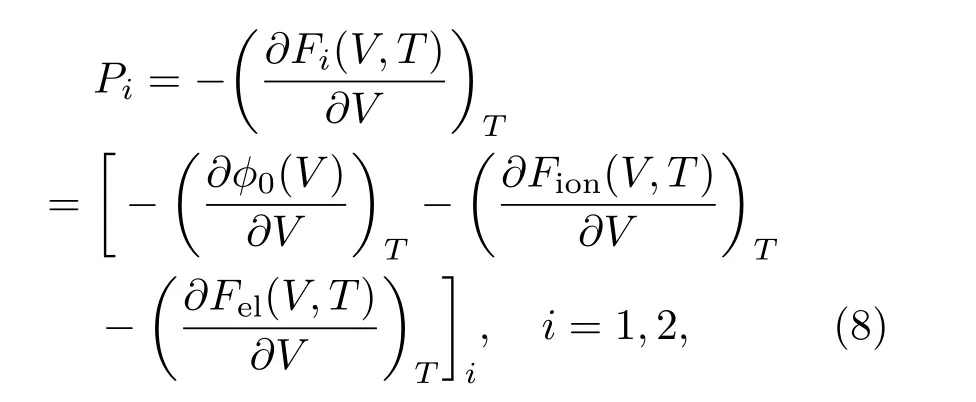
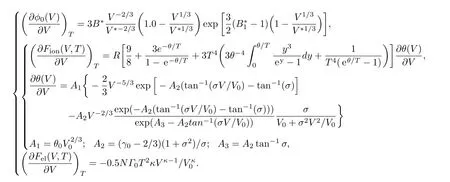
锆的本构关系采用Steinberg模型[23],本文未考虑两相本构参数的差异.对混合相区本文借鉴Hayes[21]模型做出以下假设:各相的混合物在宏观上均匀分布,但在微观上由足够大的纯相区构成,各相表面影响忽略;每个纯相区处于热力学平衡态;所有相区都处于当地的压力和热平衡条件,同一位置处各相压力和温度相同,混合物不必处于热力学平衡态;流动是绝热的.基于以上假设,第2相质量分数为ξ时混合区的比容、内能为

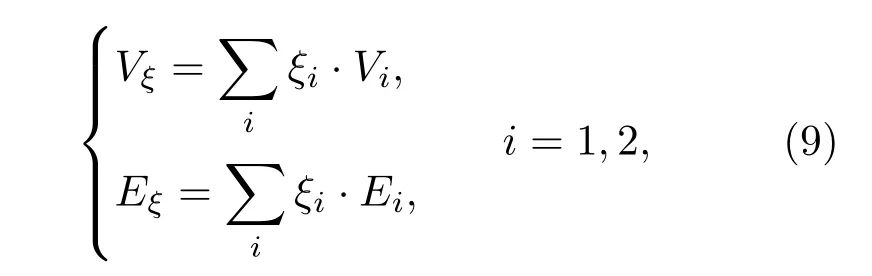
式中ξi,Vi和Ei是第i纯相区的质量分数、比容和内能.

基于上述多相状态方程和相变动力学方程,以加载应力历史为输入边界条件,开展了斜波压缩下锆的相变动力学模拟,与实验结果进行了比较,如图3所示,计算结果很好地再现了锆实验动态响应特性.但从图3(a)可以看出,蓝宝石窗口时,计算相变特征速度拐点略大于实验值,这可能与界面成核相关,本文相变动力学方程(2)暂时无法体现成核分布,下一步将利用其他方法进行深入研究.锆样品中加载面附近某单元两相质量分数历史见图3(b)所示,为自由面锆样品的计算结果,相变弛豫时间τ=30 ns.到达相变临界条件后,相变并非瞬间完成,而是随着压力提高、时间积累,新相质量分数指数增加,相变完成时间约100 ns.

每发斜波压缩实验可得到样品的一条准等熵线,计算得到的压力-相对比容线、温度-压力线和冲击Hugoniot线见图4.在压力-相对比容路径中:首先,在相变前准等熵线与冲击绝热线差异很小,这与理论预估相符;第二,准等熵压缩过程明显存在一个两相混合区域,等熵线平滑地过渡到第二相,不像Hugoniot线在相变附近存在明显的拐折,说明加载时间较长时,相变完成是需要时间的,而不是瞬间完成;第三,相变完成后,准等熵线位于冲击绝热线下方,这是由于斜波过程温升小,相同比容时压力较低.在温度-压力相图中:第一,相变前准等熵线与冲击绝热线差异很小,相变起点与冲击实验给出的相界符合;第二,相变后准等熵线位于Hugoniot线下方,这是由于相对于冲击压缩,斜波压缩过程温升较小,随着压力的增加两条线偏差越来越大,在20 GPa相差约100 K.

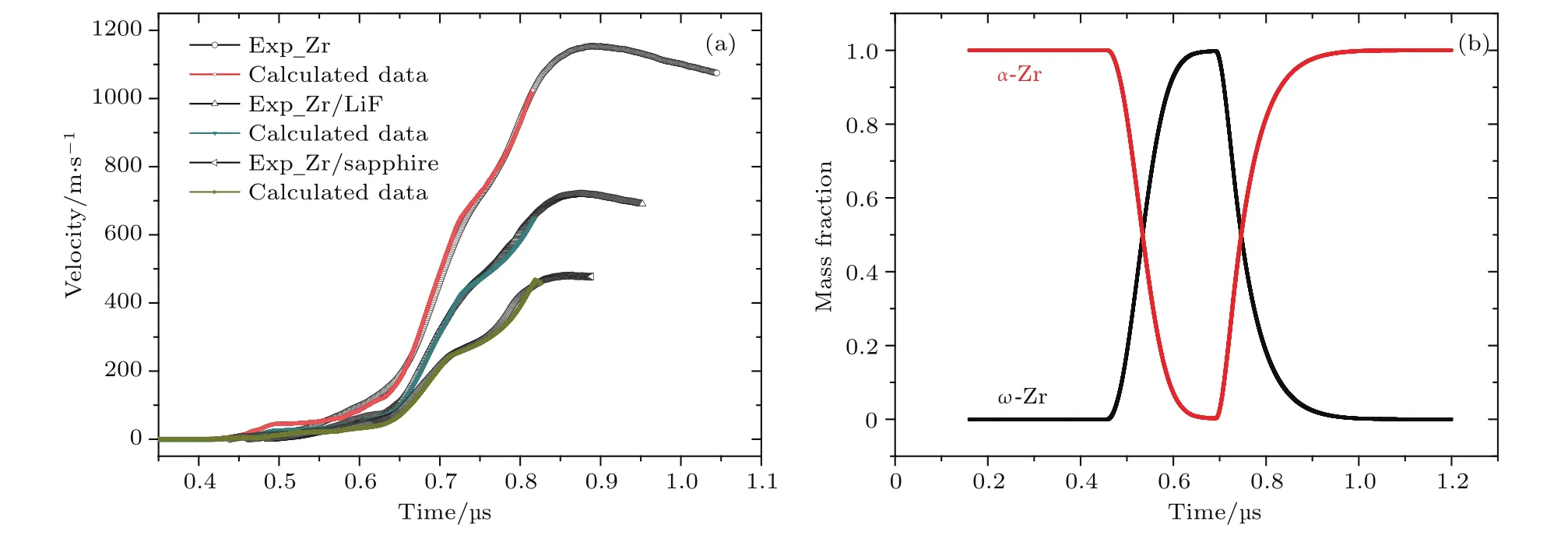
图3 数值模拟结果 (a)界面速度模拟结果;(b)两相质量分数Fig.3.Numerical results:(a)Calculated and experimental interface velocities;(b)mass fraction.

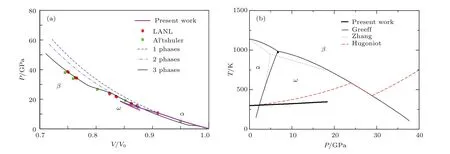
图4 斜波和冲击压缩过程对比 (a)压力-相对比容路径;(b)温度-压力相图Fig.4.Comparison of ramp wave and impact compression:(a)Pressure-relative specif i c volume;(b)temperaturepressure.

图5 声速-压力Fig.5.sound speed-pressure.

利用本文的模型及参数计算的拉氏声速-压力见图5.由图5可知,锆压缩后,首先进行弹塑性转变,声速从4.7 km/s减小到3.9 km/s;进入塑性段后而随着压力的增加声速增加,说明体模量随压力的提高而增加;相变开始后声速迅速减小约7.1%,这是相变引起的比容间断造成的,相变完成后声速恢复.

本文数值模拟以极板内表面应力历史为输入边界,由于电极内表面在电流经过时发生磁扩散、烧蚀等复杂的物理过程,现阶段还无合适的磁流体动力学程序以加载电流为输入计算整个物理过程.本文以电极靶自由面速度结合反积分或阻抗匹配方法获取加载应力历史.由于极板自由面无法反映样品、窗口中卸载阶段的稀疏反射,因此这里只计算了加载段波形.

5 结 论

通过不同声阻抗窗口匹配锆的斜波压缩相变实验和数值模拟分析,得到以下结论:

1)得到了斜波压缩下不同声阻抗窗口时锆样品/窗口含有相变信息的界面速度波剖面,低阻抗匹配时,锆相变起始对应的粒子速度约为331.0 m/s,高阻抗匹配时,该速度约为301.9 m/s;

2)基于Helmholtz自由能为基础的多相物态方程和非平衡相变动力学方程对锆的斜波压缩下相变效应进行了模拟,数值计算可以较好地模拟锆在斜波加载阶段的弹塑性转变、相变等动态响应;

3)在压力-比容平面,锆的冲击绝热线与准等熵线在相变前差异很小,从相变起始点分离,进入新相后准等熵线在冲击绝热线下方;温度-压力相图中,相变前准等熵线与冲击绝热线差异很小,相变后准等熵线位于Hugoniot线下方,且随着压力的增加两条线偏差越来越大;

4)进入相变后声速有明显的下降,这是由于相变引起的比容间断造成的,与已有实验和理论结果符合.

感谢吴刚、税荣杰、胥超、马骁和邓顺益在实验运行、维护和测速方面提供的巨大帮助.

[1]Xiao D W 2008Ph.D.Dissertation(Hefei:University of Science and Technology of China)(in Chinese)[肖大武2008博士学位论文(合肥:中国科学技术大学)]

[2]Bridgman P W 1952Proceedings of the American Academy of Arts&Sciences81 165

[3]Jamieson J C 1963Science140 72

[4]Zilbershtein V A,Nosova G I,Estrin E I 1973Phys.Met.Metallogr.35 29

[5]Xia H,Parthasarathy G,Luo H,Vohra Y K,Ruof fA L 1990Phys.Rev.B42 6736

[6]Xia H,Duclos S J,Ruof fA L,Vohra Y K 1990Phys.Rev.Lett.64 204

[7]Al’Tshuler L V,Bakanova A A,Dudoladov I P 1967Zh.Eksp.Teor.Fiz.53 1967

[8]Al’Tshuler L V,Bakanova A A,Dudoladov I P,Dynin E A,Trunin R F,Chekin B S 1981J.Appl.Mech.Tech.Ph.22 145

[9]McQueen R G,Marsh S P,Taylor J W,Fritz J N,Carter W J 1970High Velocity Impact Phenomena(New York:Academic)pp293–417

[10]Kutsar A R,Pavlovskii M N,Kamissarov V V 1982Jetp.Lett.39 1

[11]Greef fC W 2005Model.Simul.Mater.Sc.13 1015

[12]Cerreta E,Iii G T G,Hixson R S,Rigg P A,Brown D W 2005Acta Mater.53 1751

[13]Gray G T,Bourne N K 2000Shock Compression of Condensed Matter(Vol.505)(American Institute of Physics)p509

[14]Rigg P A,Greef fC W,Knudson M D,Iii G T G,Hixson R S 2009J.Appl.Phys.106 245

[15]Li Y H 2006M.S.Dissertation(Mianyang:China Academy of Engineering Physics)(in Chinese)[李英华2006硕士学位论文(绵阳:中国工程物理研究院)]

[16]Chong T,Wang G J,Tan F L,Luo B Q,Zhang X P,Wu G,Zhao J H 2014Sci.Sin.:Phys.Mech.Astron.44 1(in Chinese)[种涛,王桂吉,谭福利,罗斌强,张旭平,吴刚,赵剑衡2014中国科学:物理学力学天文学44 1]

[17]Wang G J,Luo B Q,Zhang X P,Zhao J H,Sun C W,Tan F L,Chong T,Mo J J,Wu G,Tao Y H 2013Rev.Sci.Instrum.84 015117

[18]Hall C A,Asay J R,Knudson M D,Stygar W A,Hall C A,Asya J R,Knudson M D 2001Rev.Sci.Instrum.72 3587

[19]Chong T 2012M.S.Dissertation(Mianyang:China Academy of Engineering Physics)(in Chinese)[种涛2012硕士学位论文(绵阳:中国工程物理研究院)]

[20]Tang Z P 2008Phase Transition under Shock Compression(Beijing:Science Press)p130(in Chinese)[唐志平2008冲击相变(北京:科学出版社)第130页]

[21]Hayes D B 1975J.Appl.Phys.46 3438

[22]Zuo Q H,Harstad E N,Addessio F L,Greef fC W 2006Model.Simul.Mater.Sci.14 1465

[23]Steinberg D J,Cochran S G,Guinan M W 1980J.Appl.Phys.51 1498