间隙原子H,B,C对LaFe11.5Al1.5化合物磁性和磁热效应的影响∗

杨静洁赵金良许磊张红国岳明刘丹敏蒋毅坚

1)(北京工业大学应用数理学院,北京 100124)

2)(北京工业大学材料科学与工程学院,北京 100124)

3)(北京工业大学固体微结构与性能研究所,北京 100124)

4)(北京工业大学激光工程研究院,北京 100124)

1 引 言

近年来,基于磁热效应(MCE)的磁制冷材料引起了国内外的广泛关注.由于在磁制冷领域具有巨大的应用潜能,许多具有磁热效应的磁致冷材料已被广泛地研究[1−9].在这些材料中,La(Fe,M)13(M=Si,Al等)基化合物以其巨磁熵变、居里温度(TC)可调、价格低廉、无毒害等优势迅速成为最具潜力的高性能磁致冷材料之一[10].由于La(Fe,Si)13基化合物往往具有一级相变的性质,能够产生较大的磁熵变,以往对这类化合物研究的比较多,而另一方面,随之产生的磁滞损耗却造成有效制冷能力的下降.La(Fe,Al)13基化合物一般呈二级相变,通常磁熵变值较La(Fe,Si)13基化合物小,但二级相变材料没有磁滞损耗,有利于这类材料在实际中的应用.

La(Fe,Al)13化合物的空间群为Fm-3c且具有NaZn13型晶体结构[11].在1.04 6x<1.82范围内,LaFe13−xAlx化合物为反铁磁态[12].用Co或Fe替代La能够提高LaFe13−xAlx化合物的居里温度,但会造成最大磁熵变降低[13].引入间隙原子(N,H,C,B)能够使晶格膨胀,使化合物由反铁磁态转变为铁磁态[14−23],同时,TC会随着间隙原子含量的增加而上升,磁性也随之会发生变化[10].

H,B,C等间隙原子分别对LaFe1.5Si1.5,LaFe11.5Al1.5化合物磁性和磁热效应的影响在此前已有报道,本文集中比较了几类间隙原子(H,B,C)对LaFe11.5Al1.5化合物磁性和磁热效应的影响,并分析了造成不同影响的原因.

2 实验方法

将高纯La(99.5 wt.%),Fe(99.99 wt.%),Si(99.99 wt.%),Al(99.6 wt.%)及FeB合金、FeC合金等原料按化学配比称量(考虑到La的烧损,多添加8 wt.%)在氩气气氛中进行电弧熔炼,制备出LaFe11.5Al1.5,LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5)化合物.反复熔炼四次,以确保样品的均匀性.将熔炼好的样品分别密封在充有高纯氩气的石英管中,在1223 K下退火三周,最后将退火后的样品在高温下取出,并快速在冰水中进行淬火处理.采用P-C-T实验仪在623 K和不同氢气压力下对淬火后的LaFe11.5Al1.5化合物样品进行吸氢处理.LaFe11.5Al1.5Hy化合物中H的总含量可以根据理想气体方程(PV=nRT)计算得出,P为氢气压力,V为腔室的体积,n为该腔室中氢气分子的物质的量,R是理想气体常数(R=8.3145 J/mol…K),T为化合物在氢气中的退火温度.分别采用X射线衍射仪(XRD)和振动样品磁强计(VSM)表征样品的晶体结构以及磁性.

3 结果与讨论

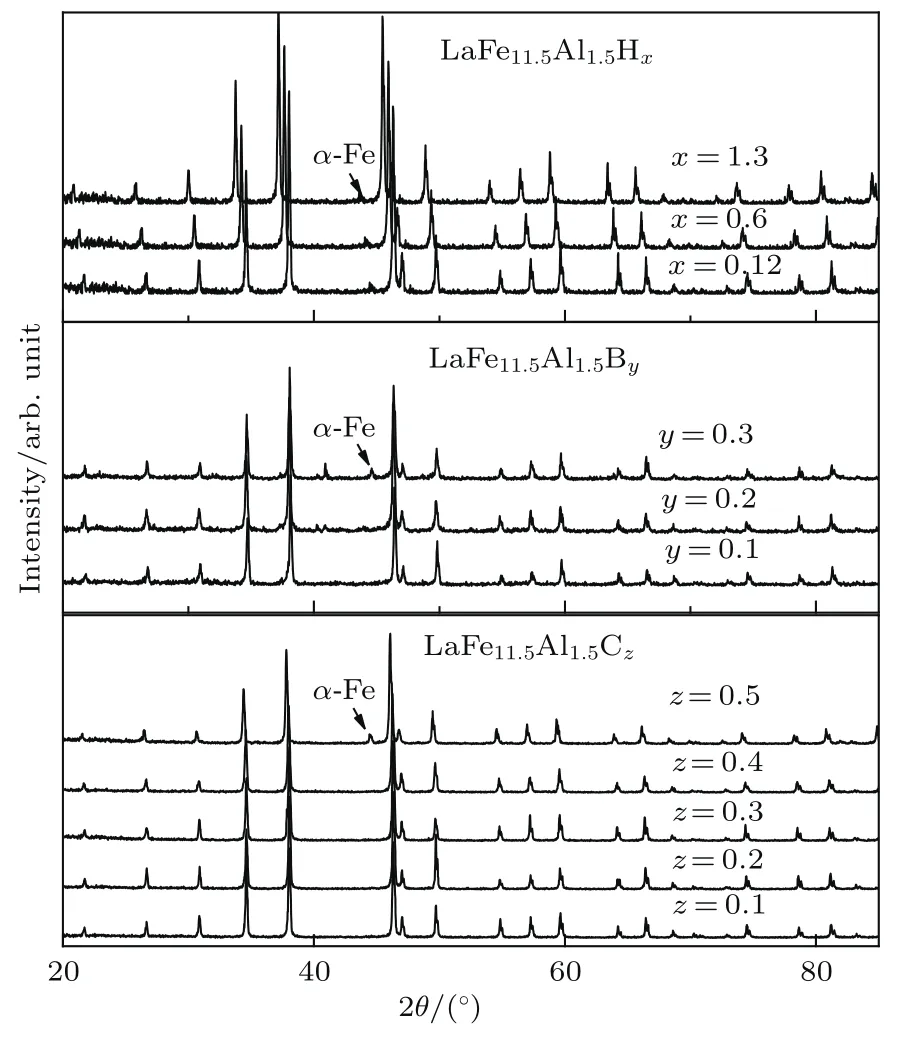
图1 LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5-Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5)化合物的XRD图谱Fig.1.XRD patterns of the LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)and LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5).

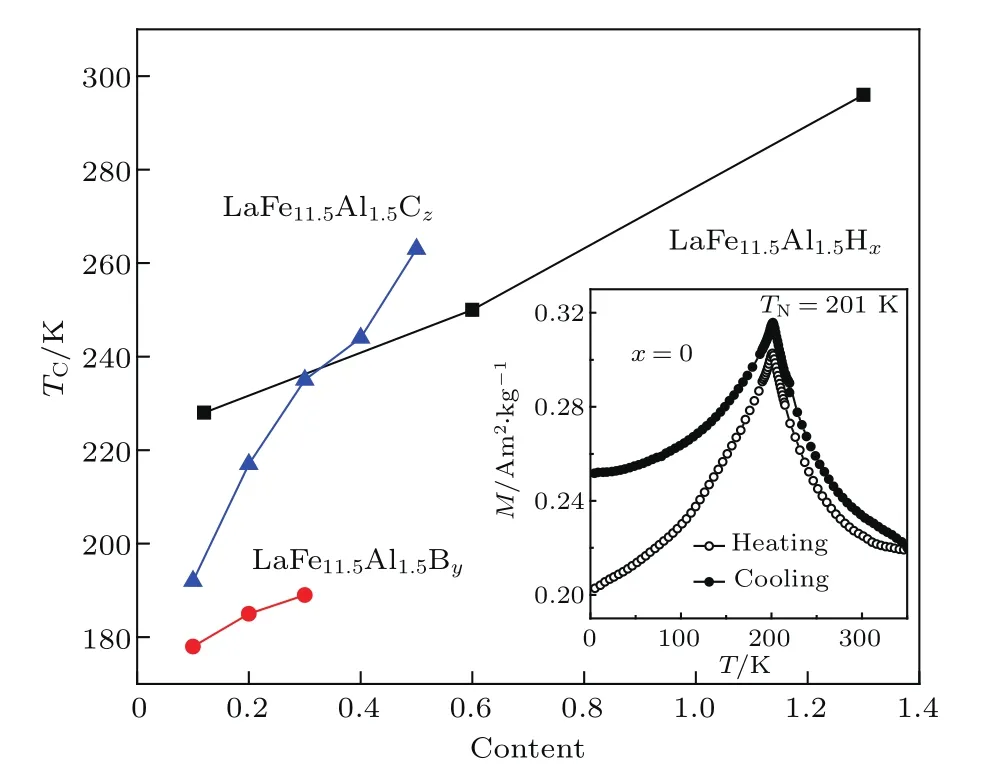
图2 LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5-Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5)化合物中居里温度TC与间隙原子浓度的关系依赖曲线,插图为在0.01 T外磁场下LaFe11.5Al1.5化合物的M-T曲线Fig.2.Curie temperatureTCas a function of interstitial atoms concentration for LaFe11.5Al1.5Hx(x=0.12,0.6 and 1.3),LaFe11.5Al1.5By(y=0.1,0.2 and 0.3)and LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4 and 0.5).The inset plots show temperature dependence of magnetization measured under a f i eld of 0.01 T for LaFe11.5Al1.5.

由图1所示XRD图谱可知,LaFe11.5Al1.5Hx(x=0,0.12,0.6,1.3),LaFe11.5Al1.5By(y=0,0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0,0.1,0.2,0.3,0.4,0.5)化合物均形成了NaZn13型单相晶体结构,其空间群为Fm-3c.间隙原子(H,B,C)的引入仅会使晶格膨胀,而不会改变其晶体结构.

图2为LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),La-Fe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5)化合物居里温度TC与间隙原子浓度的关系曲线,插图为LaFe11.5-Al1.5合金的M-T曲线.由图可知,LaFe11.5Al1.5母合金在奈尔温度TN=201 K时呈现出从反铁磁态(AFM)到顺磁态(PM)的相变.研究表明[24,25],反铁磁-铁磁转变存在Fe—Fe临界键长d∼2.45 Å,当Fe—Fe间距离小于这一临界键长时,交换作用为负,而当超过这一临界键长时,交换作用为正.引入间隙原子后,化合物出现从FM到PM的相变.说明间隙原子的引入能够增加Fe—Fe间的原子间距,从而降低甚至消除从AFM到FM的能量壁垒,使Fe—Fe键长超过临界键长d∼2.45 Å,交换作用由负变正,化合物的初始态磁性实现了从AFM到FM的转变.

居里温度TC可以定义为磁化升温过程中磁化强度对温度导数的最大值[26]. 对于LaFe11.5Al1.5Hx化合物,当H含量x由0.12增加到1.3,TC从178 K逐渐增加到189 K;对于LaFe11.5Al1.5By化合物,当B含量y由0.1增加到0.3,TC从178 K增加到189 K;对于LaFe11.5Al1.5Cz化合物,当C含量z由0.1增加到0.5,TC从191 K增加到262 K.上述间隙化合物居里温度的升高和间隙原子含量的增加基本呈线性关系.间隙原子(H,B,C)的含量和居里温度TC的关系可以分别拟合成以下方程:

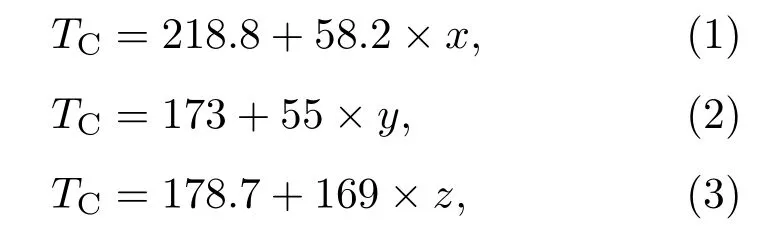
其中,x,y,z分别为H,B,C的原子含量.间隙原子H,B,C对居里温度TC的影响主要包括两个方面.一方面,间隙原子的引入使晶格膨胀,晶胞参数增加,由此导致铁原子3d电子波函数的交叠减小,3d能带带宽变窄,Fe—Fe原子之间的交换作用增强,居里温度TC升高;另一方面,间隙原子和Fe原子之间存在轨道杂化作用,会使TC降低.由图2可以看出,随着间隙原子(H,B,C)含量的增加,间隙化合物居里温度均逐渐升高,这表明晶格膨胀超过轨道杂化对居里温度的影响,起主要作用,H,B,C和Fe原子轨道电子的杂化作用起次要作用[27].B原子半径最大,因此,B原子和Fe原子之间的轨道电子杂化作用最强,造成方程(2)斜率最小.C的原子半径比氢大,C原子和Fe原子之间的轨道电子杂化作用较强,但是C碳原子造成的晶格膨胀又比H原子强,使得方程(1)的斜率比方程(3)的小.

图3为LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5-Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5)化合物中居里温度TC和晶格常数的关系.由图可知,居里温度TC随着晶格常数的增大而升高.图中LaFe11.5Al1.5Cz的TC随晶格常数的增长斜率与LaFe11.5Al1.5By以及LaFe11.5Al1.5Hx的TC随晶格常数的增长斜率基本相同,说明TC的变化主要是由晶格膨胀引起的,受到间隙原子其他因素影响较小.

图3 LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4,0.5)化合物中居里温度TC和晶格常数的关系Fig.3.Curie temperatureTCas a function of lattice constant for LaFe11.5Al1.5Hx(x=0.12,0.6 and 1.3),LaFe11.5Al1.5By(y=0.1,0.2 and 0.3)and LaFe11.5Al1.5Cz(z=0.1,0.2,0.3,0.4 and 0.5).

图4为LaFe11.5Al1.5Hx(x=0,0.12,0.6,1.3),LaFe11.5Al1.5By(y=0,0.1,0.2,0.3)和LaFe11.5-Al1.5Cz(z=0,0.1,0.2,0.3,0.4,0.5)在5 K时的磁化曲线(M-H).由图可知,母合金LaFe11.5Al1.5的磁矩随着外加磁场的增加先缓慢增大,但当外加磁场达到约4.9 T时,磁矩突然大幅度增加,即迅速发生了由外磁场诱发的从AFM到FM的变磁转变.磁场降低过程中,FM一直持续到1.6 T时才转变为AFM,出现大的磁滞现象.与母合金LaFe11.5Al1.5不同,所有的LaFe11.5Al1.5Hx,LaFe11.5Al1.5By和LaFe11.5Al1.5Cz样品均表现为典型的FM,它们在1 T的外加磁场下便能够达到饱和.此外,间隙原子(H,B,C)的引入可以提高饱和磁化强度(Ms).Ms和间隙原子(H,B,C)的含量之间的关系可以拟合成以下方程:

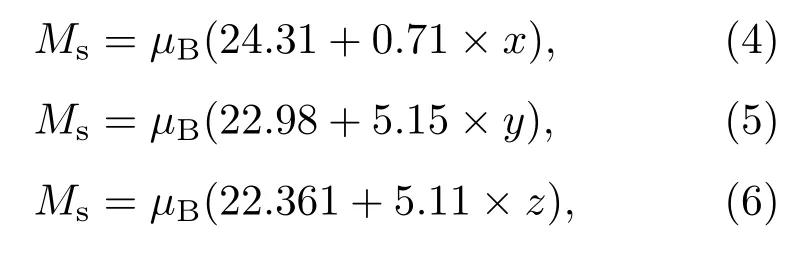
其中x,y,z分别表示间隙原子H,B,C的含量.间隙原子的引入对合金LaFe11.5Al1.5磁化强度的影响也主要表现为两个方面:一方面,间隙原子(H,B,C)的引入会引起晶格膨胀,Ms增加;另一方面,原子之间的轨道电子杂化作用会导致Ms降低.B原子半径最大,B的2p电子和Fe的3d电子间的轨道电子杂化作用最强.图4表明,引入间隙原子后化合物的Ms增加,即晶格体积膨胀效应对Ms的影响超过轨道杂化,起主要作用.因此,LaFe11.5Al1.5化合物的磁性对体积的变化比较敏感.

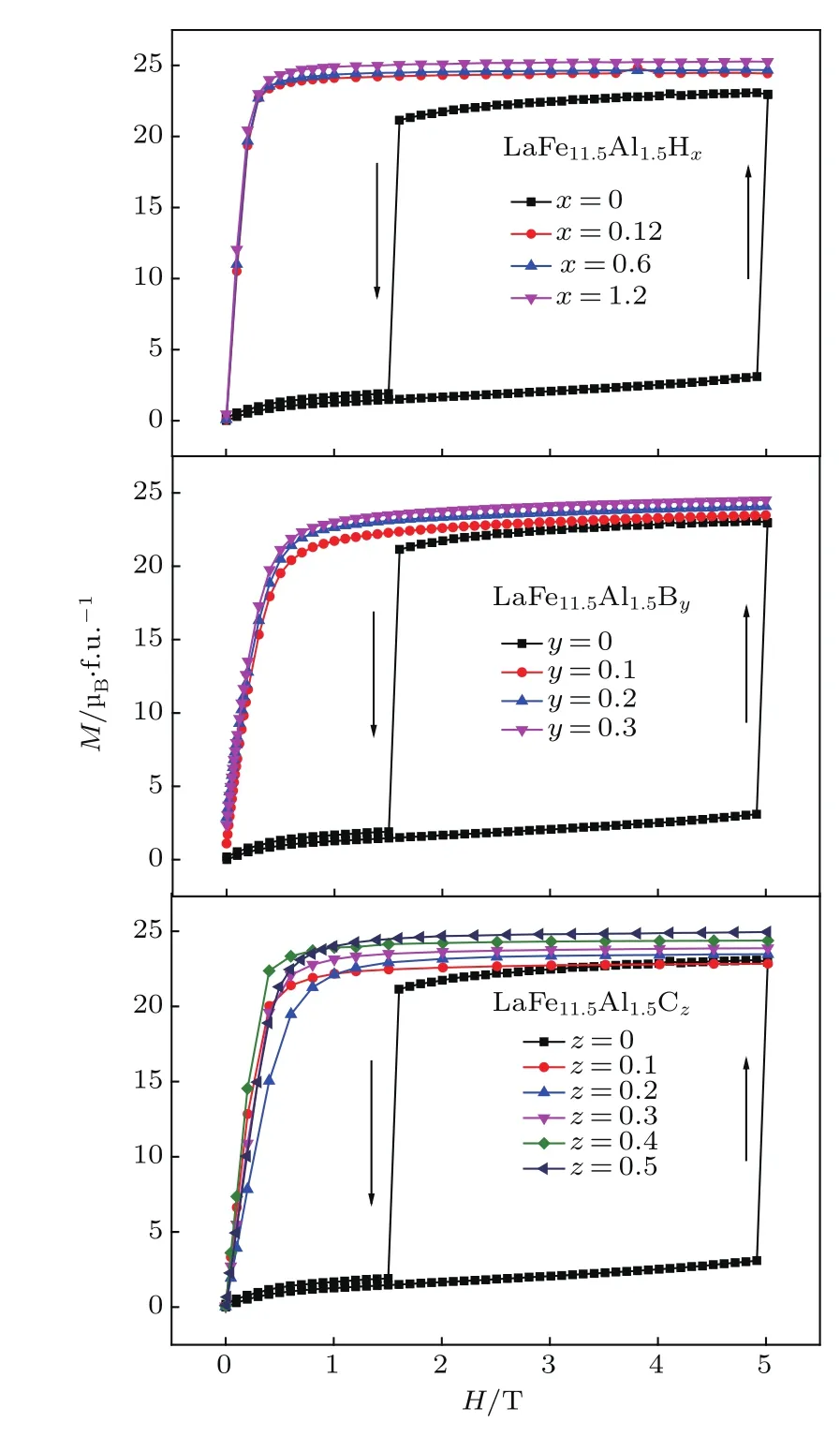
图4 LaFe11.5Al1.5Hx(x=0,0.12,0.6,1.3),LaFe11.5Al1.5-By(y=0,0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0,0.1,0.2,0.3,0.4,0.5)在5 K时的M-H曲线Fig.4.Magnetization dependence of magnetic f i eld measured at 5 K for LaFe11.5Al1.5Hx(x=0,0.12,0.6 and 1.3),LaFe11.5Al1.5By(y=0,0.1,0.2 and 0.3)and LaFe11.5Al1.5Cz(z=0,0.1,0.2,0.3,0.4 and 0.5).

磁性基态的转变由磁相变温度附近自由能与温度和磁场之间的关系决定[28].朗道模型可以用来表征不同间隙原子(H,B,C)对相变产生的影响.在该模型中,自由能F(M,T)、磁化强度M和磁场µ0H三者的关系可以进行如下的朗道展开:

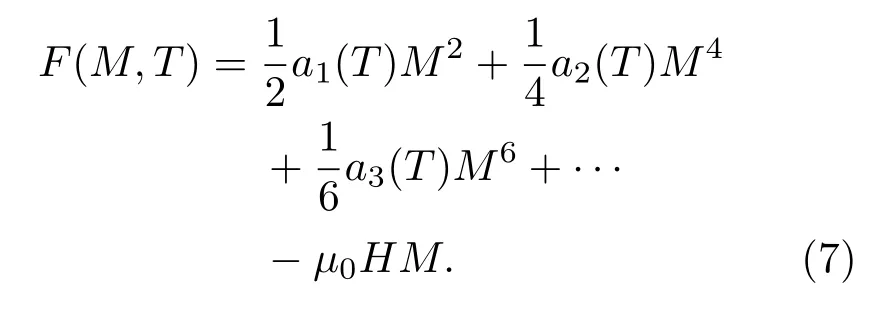
由此得到朗道系数和温度T间的关系式:

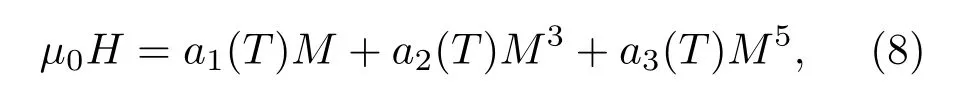
上述系数a1(T),a2(T)和a3(T)可依据方程(7)通过拟合M-H曲线得到.a1(T)是磁化率的倒数,在TC处达到极小值,为正值.a2(T)在TC处的正负决定了相变的级数,当a2(T)>0时对应二级相变,当a2(T)<0时对应一级相变[29].

图5为LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5-Cz(z=0.2,0.4)化合物的朗道系数与温度的关系曲线,可以看出,所有化合物的a1(T)在TC处达到极小值,且均为正值.LaFe11.5Al1.5Hx(x=0.12,0.6,1.3)的朗道系数a2(T)在TC处的值分别为0.12,−0.06和−0.37,说明随着H含量的增加,相变性质从二级相变转变为弱一级相变.与之不同,对LaFe11.5Al1.5By化合物而言,y=0.1,0.2和0.3的三个样品在TC处的朗道系数a2(T)的值分别是−0.83,0.55和0.97,而对于LaFe11.5Al1.5Cz化合物而言,当z为0.2和0.4时,TC处a2(T)的值分别为−0.85和0.15,说明随着B原子和C原子含量的增加,在TC处均发生了由弱一级相变到二级相变的转变.

图6为LaFe11.5Al1.5Hx(x=0.12,0.6,1.3)化合物相变温度附近的M-H曲线,值得注意的是,升场曲线(用“◦”表示)和降场曲线(用“+”表示)基本重合,说明弱一级相变基本没有磁滞后,这有利于获得更大的有效制冷能力.

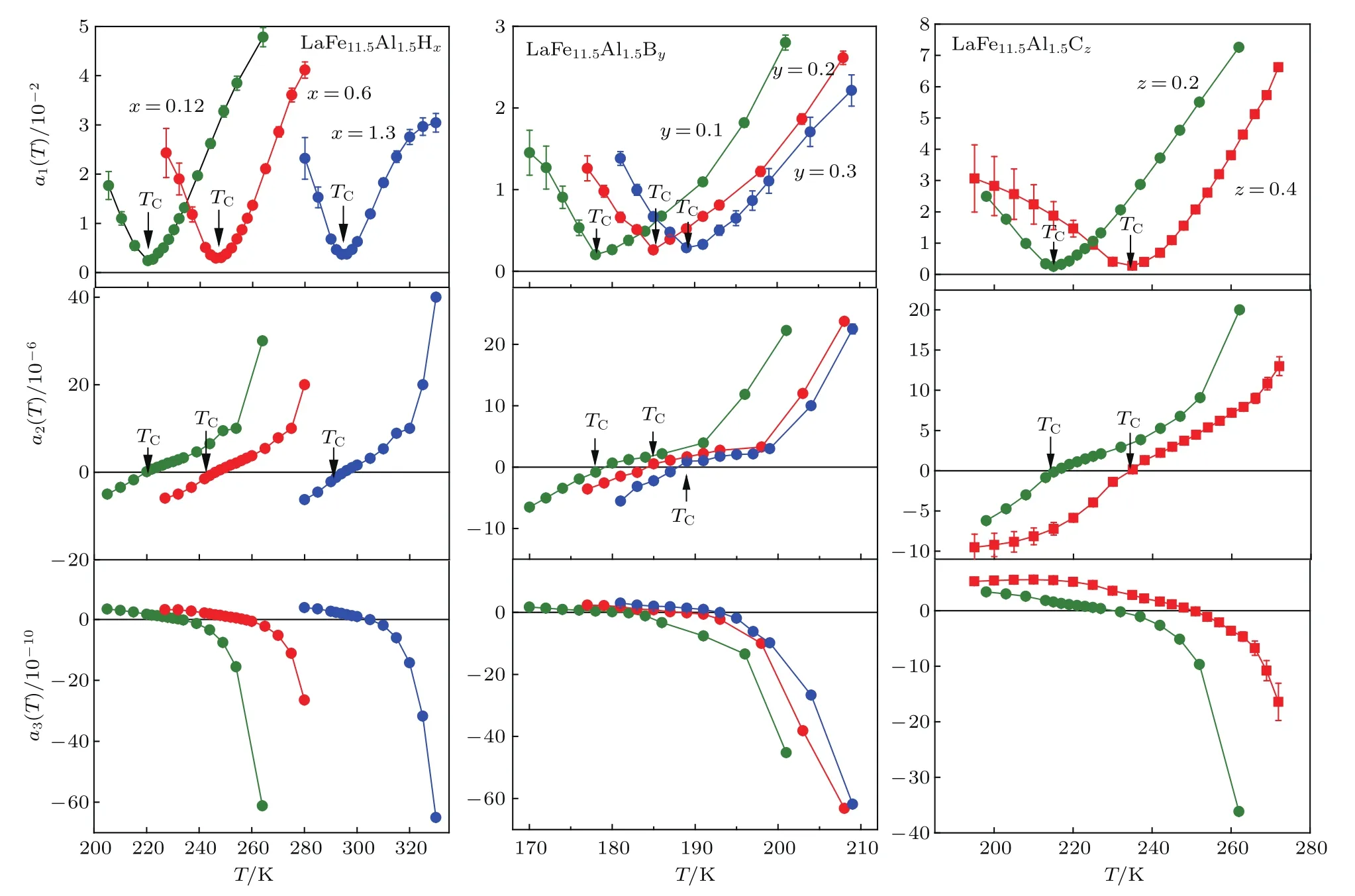
图5 LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.2,0.4)化合物的朗道系数与温度的关系Fig.5.Temperature dependence of Landau coefficients for LaFe11.5Al1.5Hx(x=0.12,0.6 and 1.3),LaFe11.5Al1.5By(y=0.1,0.2 and 0.3)and LaFe11.5Al1.5Cz(z=0.2 and 0.4).

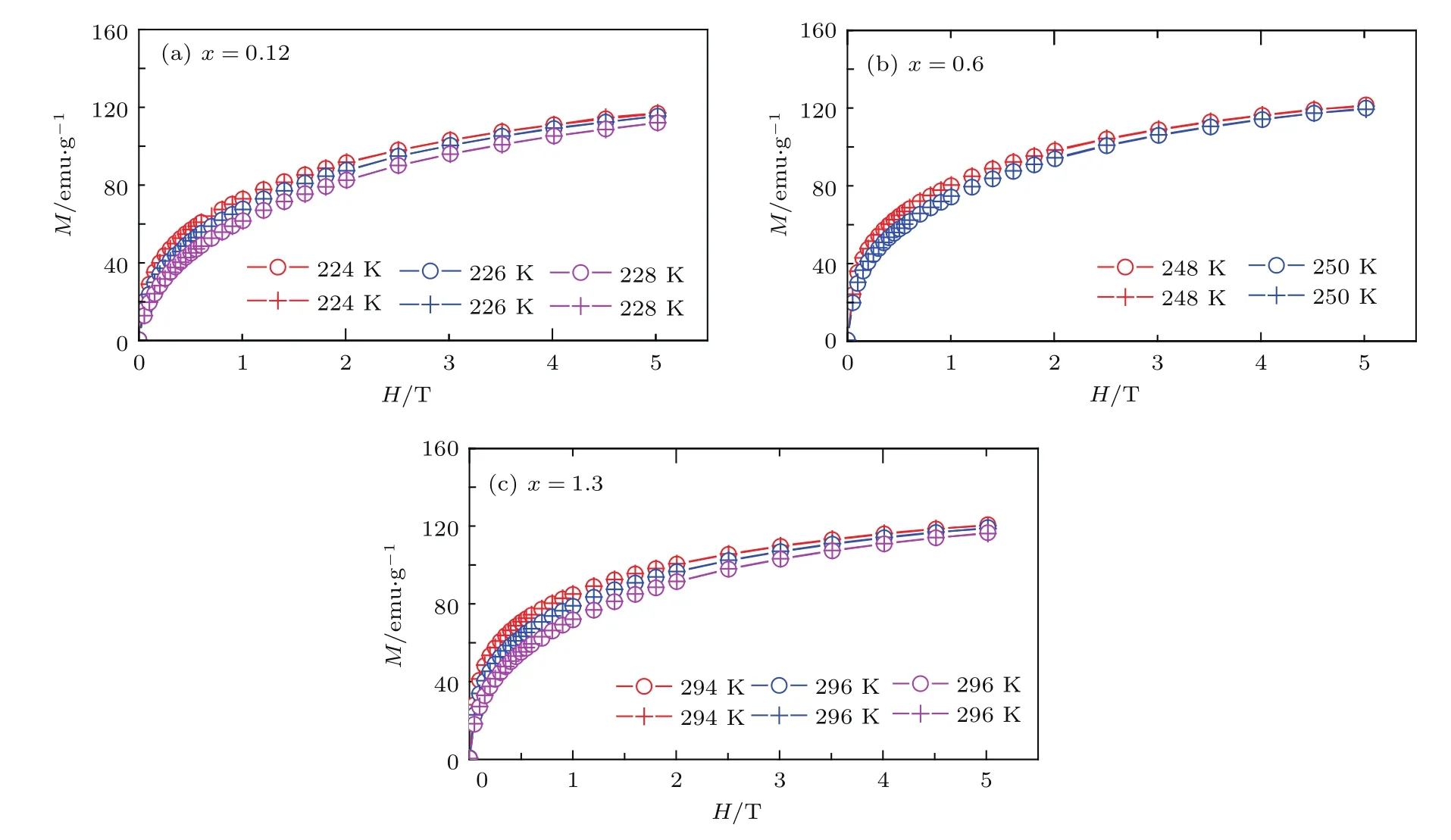
图6 LaFe11.5Al1.5Hx(x=0.12,0.6,1.3)化合物相变温度附近的M-H曲线,其中“◦”表示升场过程,“+”表示降场过程Fig.6.Magnetization isotherms of LaFe11.5Al1.5Hx(x=0.12,0.6 and 1.3)measured in the vicinity of theTCwith increasing and decreasing magnetic f i eld.

利用Maxwell关系[30,31],由M-H曲线,可以计算出LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5-Al1.5Cz(z=0.1,0.2,0.4,0.5)化合物的等温磁熵变.图7为LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5-Al1.5Cz(z=0.1,0.2,0.4,0.5)化合物在0—2 T和0—5 T磁场变化下磁熵变随温度的变化曲线.从图7可以看出,在0—5 T外磁场下,LaFe11.5Al1.5-Hx化合物的最大磁熵变(−∆SM)从x=0.12时的10.1 J/kg…K增加到x=1.3的12.3 J/kg…K.对于LaFe11.5Al1.5Bx化合物而言,x由0.1变到0.3时,−∆SM由9.6 J/kg…K下降到9.2 J/kg…K,对于LaFe11.5Al1.5Cy化合物而言,y由0.1变到0.2时,−∆SM由9.6 J/kg…K升高到10.8 J/kg…K,随后又下降到y=0.5的10.1 J/kg…K.LaFe11.5Al1.5Cz化合物的最大磁熵变值与Gd(TC=293 K,在∆H=5 T时,−∆SM约9.8 J/kg…K,在∆H=2 T时,−∆SM约4.5 J/kg…K)相近,甚至比Gd还要大一些.

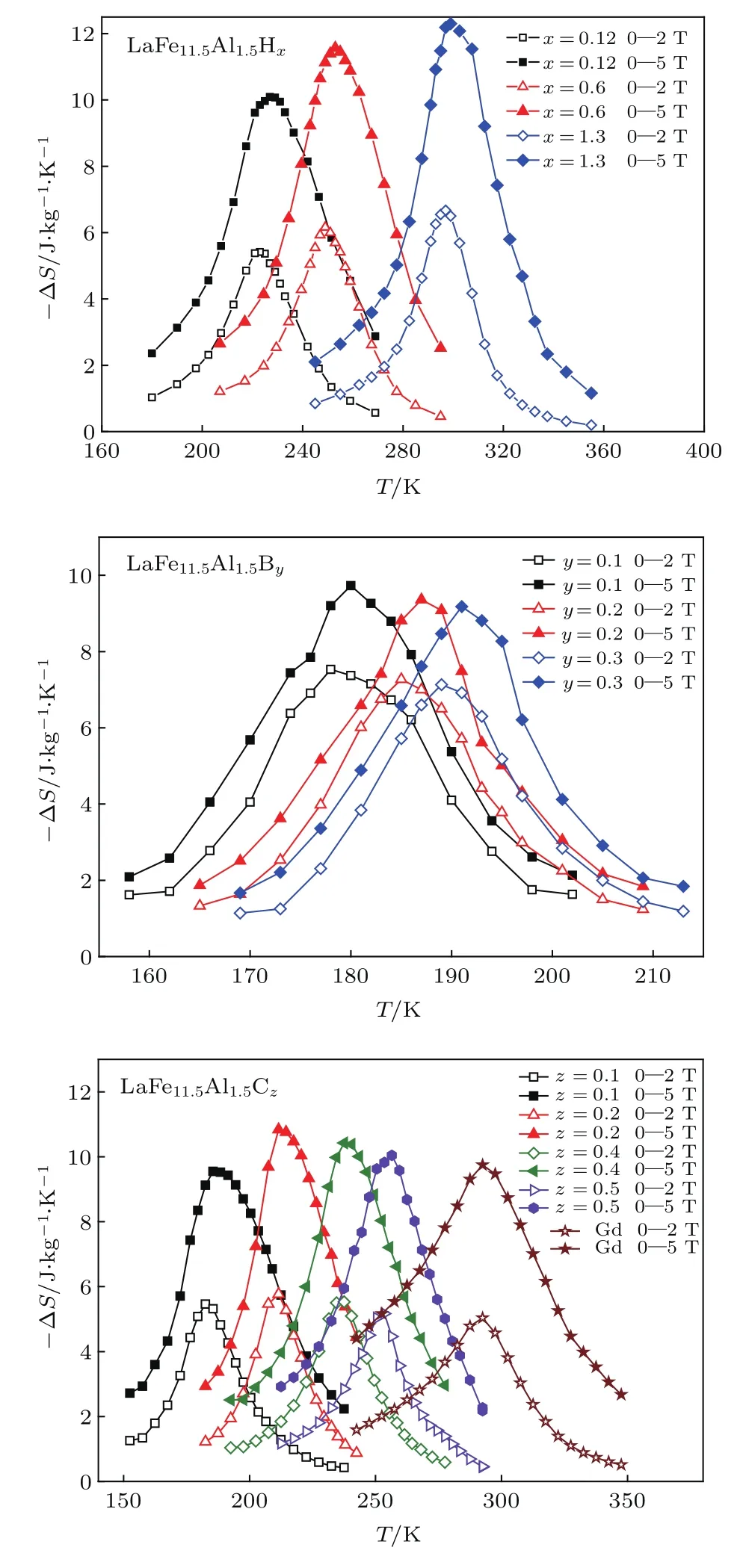
图7 LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和LaFe11.5Al1.5Cz(z=0.1,0.2,0.4,0.5)化合物在0—2 T和0—5 T磁场变化下磁熵变随温度的变化Fig.7.Isothermal magnetic entropy change dependence of temperature under the f i eld changes of 0–2 T and 0–5 T for LaFe11.5Al1.5Hx(x=0.12,0.6 and 1.3),LaFe11.5Al1.5By(y=0.1,0.2 and 0.3)and LaFe11.5Al1.5Cz(z=0.1,0.2,0.4 and 0.5).

根据Gschneidner等[27]提出的方法,计算−∆SM与T之间关系以半峰宽为温度区间所包围的面积,结合(9)式计算了LaFe11.5Al1.5Hx(x=0.12,0.6,1.3),LaFe11.5Al1.5By(y=0.1,0.2,0.3)和 LaFe11.5Al1.5Cz(z=0.1,0.2,0.4,0.5)化合物的制冷能力:

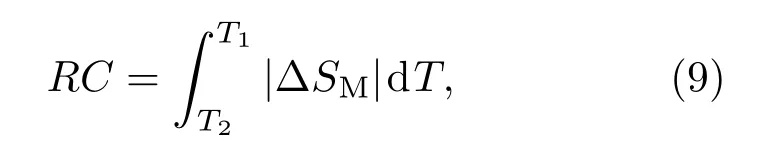
式中,T1和T2分别是半峰宽两端的温度.LaFe11.5Al1.5Hx化合物的制冷能力在x=0.12时为253.5 J/kg,在x=0.6时为259.2 J/kg,在x=1.3时为246 J/kg.LaFe11.5Al1.5By化合物的制冷能力从y=0.1时的116.4 J/kg降低为y=0.3时的91 J/kg.另外,LaFe11.5Al1.5Cz化合物的制冷能力从z=0.1时的230.4 J/kg降为z=0.5时的222.2 J/kg,说明LaFe11.5Al1.5H0.6化合物才是最具潜力的磁制冷材料.

4 总 结

本文研究了LaFe11.5Al1.5化合物引入间隙原子(H,B,C)的磁性和磁热效应.研究表明,引入间隙原子后,化合物的磁基态由反铁磁转变为铁磁,同时伴随TC和Ms的上升.值得注意的是,间隙H原子与间隙B,C原子导致相反的相变过程,即随着H原子含量的增加,相变性质由二级转变为弱一级相变,而增加间隙B原子或C原子,相变性质却从弱一级转变为二级相变.此外,在0—5 T外磁场下,LaFe11.5Al1.5H1.3,LaFe11.5Al1.5B0.1,LaFe11.5Al1.5C0.2化合物的最大磁熵变分别达到12.3,9.6和10.8 J/kg…K.LaFe11.5Al1.5H0.6,LaFe11.5Al1.5B0.1,LaFe11.5Al1.5C0.1化合物的制冷能力分别为259.2,116.4和230.4 J/kg.因此,LaFe11.5Al1.5H0.6化合物是最具潜力的室温磁制冷材料.

[1]Gschneidner Jr K A,Pecharsky V K,Tsokol A O 2005Rep.Prog.Phys.68 1479

[2]Pecharsky V K,Gschneider Jr K A 1997Phys.Rev.Lett.78 4494

[3]Tegus O,Brück E,Buschow K H J,de Boer F R 2002Nature415 150

[4]Hu F X,Shen B G,Sun J R,Cheng Z H,Rao G H,Zhang X X 2001Appl.Phys.Lett.78 3675

[5]Shen B G,Sun J R,Hu F X,Zhang H W,Cheng Z H 2009Adv.Mater.21 4545

[6]Liu D M,Huang Q Z,Yue M,Lynn J W,Liu L J,Chen Y,Wu Z H,Zhang J X 2009Phys.Rev.B80 174415

[7]Wada H,Tanabe Y 2001Appl.Phys.Lett.79 3302

[8]Yue M,Li Z Q,Wang X L,Liu D M,Zhang J X,Liu X B 2009J.Appl.Phys.105 07A915

[9]Zhang D K,Zhao J L,Zhang H G,Xu M F,Yue M 2014J.Supercond.Nov.Magn.27 1899

[10]Shen B G,Hu F X,Dong Q Y,Sun J R 2013Chin.Phys.B22 017502

[11]van der Kraan A M,Buschow K H J,Palstra T T M 1983Hyperf i ne Int.16 717

[12]Palstra T T M,Nieuwenhuys G J,Mydosh J A,Buschow K H J 1985Phys.Rev.B31 4622

[13]Hu F X,Shen B G,Sun J R,Cheng Z H 2001Phys.Rev.B64 012409

[14]Moze O,Kockelmann W,Liu J P,de Boer F R,Buschow K H J 1999J.Magn.Magn.Mater.195 391

[15]Moze O,Kockelmann W,Liu J P,de Boer F R,Buschow K H J 2000J.Appl.Phys.87 5284

[16]Wang F,Chen Y F,Wang G J,Sun J R,Shen B G 2004J.Phys.:Condens.Matter16 2103

[17]Chen J,Zhang H W,Zhang L G,Dong Q Y,Wang R W 2006Chin.Phys.15 845

[18]Zhang D K,Zhao J L,Zhang H G,Xu M F,Yue M 2014J.Alloys Compd.591 143

[19]Zhang D K,Zhao J L,Zhang H G,Yue M 2014Acta Phys.Sin.63 197501(in Chinese)[张登奎,赵金良,张红国,岳明2014物理学报63 197501]

[20]Zhang D K,Zhao J L,Shen J,Zhang H G,Yue M 2014J.Appl.Phys.115 183908

[21]Liu J P,Tang N,de Boer F R,de Chatel P F,Buschow K H J 1995J.Magn.Magn.Mater.140 1035

[22]Irisawa K,Fujita A,Fukamichi K,Yamazaki Y,Iijima Y 2002J.Appl.Phys.91 8882

[23]Irisawa K,Fujita A,Fukamichi K,Yamazaki Y,Iijima Y,Matsubara E 2001J.Alloys Compd.316 70

[24]Jia L,Sun J R,Shen J,Gao B,Zhao T Y,Zhang H W,Hu F X,Shen B G 2011J.Alloys Compd.509 5804

[25]Li Z W,Morrish A H 1997Phys.Rev.B55 3670

[26]Cam Thanh D T,Brück E,Tegus O,Klaasse J C P,Gortenmulder T J,Buschow K H J 2006J.Appl.Phys.99 08Q107

[27]Fujii H,Sun H 1995 in:Buschow K H J ed.Handbook of Magnetic Materials(vol.9)(Amsterdam:Elsevier)pp303–311

[28]Liu X B,Altounian Z,Ryan D H 2004J.Phys.D:Appl.Phys.37 2469

[29]Liu X B,Ryan D H,Altounian Z 2004J.Magn.Magn.Mater.270 305

[30]Sun J R,Hu F X,Shen B G 2000Phys.Rev.Lett.85 4191

[31]Caron L,Ou Z Q,Nguyen T T,Cam Thanh D T,Tegus O,Bruck E 2009J.Magn.Magn.Mater.321 3559