浅谈信息技术展示高中数学知识和发展过程的案例研究

广东省乳源瑶族自治县高级中学 赵明亮

利用现代信息技术手段可以生动地呈现难度较大的教学内容，对知识的形成和发展可以进行直观的展现，能够有效地解决学生在学习中存在的问题，增强学生对数学的学习兴趣，提高学生的数学思维及能力；利用信息技术进行数学实验教学，能促进学生有效探究问题的本质，加深对概念、定理及性质定理的理解；利用信息技术手段，还可以实现学生的学习方式的转变，促进学生之间的交流与合作，培养学生进行自主合作探究性学习。

一、在信息技术的支持下的数学教学方式发生深刻的变化

使用信息技术进行数学教学，可以为学生创造出图文并茂、丰富多彩、即时反馈的学习环境。在这样的环境中，学生对新知识的构建可以在自己观察、实验、猜测、推理、交流、反思等过程中完成。信息技术的引入给学生的刺激是多样性的，既看得见，又听得着，还可以自己动手操作，这有利于调动学生的积极性和求知欲，对数学知识的获取和保持具有重要意义，也是数学教学方式与学习方式转变的具体体现。

案例一.在概率的教学中，书本101页向我们提出这样一个问题：取一个边长为2a的正方形及其内切圆，随机地向正方形丢一粒豆子，求豆子落在圆内的概率。解决本题其实不难，学生基本都知道所求的概率为圆的面积除于正方形的面积，即然而当老师提出可否用此模型求出π的近似值时，很多学生都懵了。有的学生提出疑问：π的值不是已经知道了吗，怎么还要估计。少数学生提出假设，如果能算出豆子落在圆内概率为m，那么利用就可以算出π=4m了。那么这时又出现了一个问题：怎么计算豆子落在圆内的概率呢？这时有学生想到做大量的实验，用频率估计概率。这的确是一个好想法，但是这个大量的实验是多少次？这个大量实验是否会因为人为因素使结果产生偏差呢？而你有这个信心去完成吗？学生都在交头接耳地讨论怎么做。这时我打开几何画板，给学生在电脑中演示这种重复试验（如图1）。虽然制作过程有点复杂，但是操作起来非常方便。

图（1）

当学生看完演示过程后，都恍然大悟，原来用几何画板还能快速地做模拟实验，而且非常直观地体现出实验过程和结果。对于上述思想方法在2017韶关二模文科试题14题中就有所体现。题目是：历史上有人向画有内切圆的正方形纸片上丢芝麻来估计圆周率的值，如果随机地向纸片上撒一把芝麻，1000粒落在正方形上的芝麻有778粒落在正方形的内切圆内，那么通过此模拟实验计算出π的估计值为____。

二、在信息技术支持下有利于探究知识的发生过程，提高学习效率

信息技术在处理数据上有非常大的优势，利用excel可以简化烦琐的数据处理，让学生能轻松地解决问题，提高课堂效率，提高学生的兴趣。

案例二.《线性回归方程》的教学

在必修3统计模块的线性回归方程教学中，在判断两个变量是否具备线性相关关系，要将给出的数据作出散点图进行判断。而人工绘制散点图难度较大，尤其当数据较多和数据以非整数形式出现的时候，人工绘制出的散点图会产生人为的偏差，课堂不但枯燥，而且费时费力。引入信息技术对数据处理能简化烦琐数据带来的负面影响，而且让学生操作，可以提高学生的数据处理能力，提高学生的积极性。下面是本节课的部分教学片段。

请同学们看73页的例题1。下面教同学们利用excel处理数据求线性回归方程的方法，同学们可以体验下用excel处理数据带来的方便。第一步：打开excel表格，将数据分两行对应输入到excel表格中，第二步：选中所输入的数据，点击“插入”中的图表按钮，选择“xy散点图”，这样就呈现出了输入数据所对应的散点图。第三步：根据画出的散点图判断出变量具有线性相关关系，接下来利用excel中函数功能，在空白处点击函数按钮，在选择类别中勾出统计，选择“slope”这个函数，按照提示分别框起y和x对应的数据，点击确定就出现了a的值，再次选择统计中的“intercept”这个函数，按照提示再次框起y和x对应的数据，点击确定就出现了b的值。这时就求出了线性回归方程了。如图（2）

图（2）

当学生看到利用excel表格三步就能解决所有问题，大家都觉得很神奇。当老师提出有哪位同学想利用excel表格处理75练习第二题的时候，学生都跃跃欲试，最后由钟文飘和郑健同学上来展示。展示的情况见图（3）。从这个教学片段中发现，信息技术的运用，很好地解决了统计中烦琐数据带来的问题。信息技术的使用优化了课堂教学，创新了课堂教学模式。通过学生自己的操作，传统的枯燥的数据处理变成了生动的有趣活动课，提高了学生的学习兴趣，也充分体现信息技术支持下的高水平学习过程。

图（3）

三、借助信息技术探究高考题命制过程

信息技术的引入可以让我们通过动画来发现一些结论性的东西，而这些结论也正是命题人命题的方向。通过信息技术可以让我们探究命题人员对高考题的命题思想和命题过程。

案例三.我们一起来猜想2014年全国甲卷（文）第21题这道题命题人的命题思路。题目是：已知函数f（x）=x3-3x2+ax+2，曲线y=f（x）在点（0，2）处的切线与x轴交点的横坐标为-2。

（1）求 a。（2）证明：当 k＜1 时，曲线y=f（x）与直线y=kx-2只有一个交点。

我们先来看第一问，命题人以（0，2）这个点来选择命题是因为这个点是函数y=f（x）图像与y轴的交点，也是函数图像唯一的一个定点。那么为什么选择考查此处的切线呢？我们利用几何画板作出函数y=f（x）在（0，2）处的切线。通过动画我们发现随着a的变化，函数y=f（x）在（0，2）处的切线也是在变化的，但是当a=1时，切线恰好过点（-2，0），所以命题人就用这个特殊的值进行命题，这时第一问的设问就顺理成章了。如图（4）

图（4）

对于第二问的设问就更加巧妙，首先我们来思考下为什么命题人会选择y=kx-2这样一条直线？其实这条直线不是平白无故出现的，而是命题人通过计算精心设计出来的。首先还是找函数 f（x）=x3-3x2+x+2图像上特殊的点，我们发现该函数与x轴的交点恰好是（2，0）。通过计算，我们求出函数y=f（x）在x=2处的切线方程为 y=x-2，刚好过（0，-2）。并且发现过（0，-2）向函数y=f（x）图像作切线巧好只有一条，所以命题人就选择过定点（0，-2）的直线y=kx-2作为命题基础。直线y=kx-2已经设出来了，那么试题的考查就应该围绕参数k来开展，命题的原理还是一样，通过变化找不变的量。通过变化k值命题人发现：当k＞1时，函数y=kx-2与函数y=f（x）交点的个数是2个或3个，交点的个数不确定会加大命题难度。当k=1时，此时的交点有两个，此时命题又太过简单。当k＜1时，通过动画我们发现两曲线交点的个数有且只有一个，符合命题要求。题目命完之后当然还要验证高中生用现有的知识能否解决这个问题。通过论证，第二问的设问学生可以通过已学的知识进行解答，而且体现了数学中一些重要的思想方法，难度适中，完全符合高考题型的要求。如图（5）

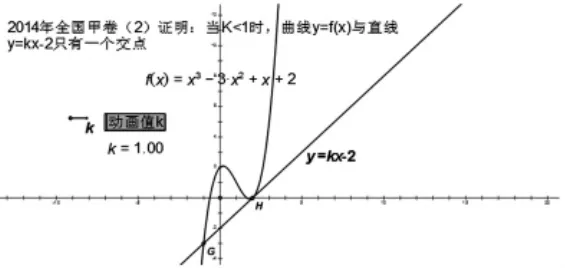
图（5）

这些案例向我们充分地展示了利用信息技术，可以准确地把握命题人的命题思想和方法，也充分地体现了信息技术在命题过程中起到的作用。信息技术的利用不只局限于解决已知的问题，而是深层次地去发现未知的问题。只有充分地去探索未知世界，才能把信息技术的作用发挥到极致。