笛卡尔乘积图Cm×Cn的符号边domatic数

董启启, 陈忠，李向军 (长江大学信息与数学学院，湖北 荆州 434023)

谭来军 (中国石油测井有限公司技术中心，陕西 西安 710077)

记无向图G=(V,E)，V和E分别是图G的顶点集和边集，NG(e)表示图G中与边e相邻边的集合，NG[e]=NG(e)∪{e}，Cn表示阶为n的圈。笛卡尔乘积图Cm×Cn，其顶点集是V(Cm)×V(Cn)，对x1，y1∈V(Cm)，x2,y2∈V(Cn)，顶点(x1，x2)与(y1,y2)相邻当且仅当x1=y1且x2y2∈E(Cn)或x2=y2且x1y1∈E(Cm)。下面笔者考虑Cm×Cn的符号边domatic数，未说明的符号及术语详见文献[1]。

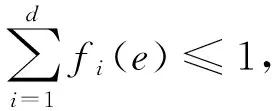
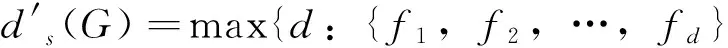
李金强等[4] 确定了笛卡尔乘积图K2×Cn及C3×Cn的符号边domatic数。对于Cm×Cn(n≥m≥4)的符号边domatic数，下面笔者给出其上界及下界。

1 Cm×Cn的符号边domatic数上界

引理1[3] 图G的符号边domatic数是一个奇数。

引理2[3] 令δ′(G)=min{|NG[e]|:e∈E(G)}，则有：

考虑笛卡尔乘积图G=Cm×Cn，为叙述方便，将其顶点看作m×n点阵，记为{xi,j:i∈{0,1,…,m-1},j∈{0,1,…,n-1}}。Cm、Cn分别为第二角标和第一角标相同的点导出子图，第一角标和第二角标的加减法分别为模m和模n运算。

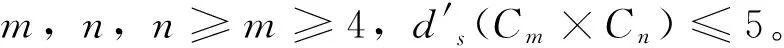
证明令G=Cm×Cn，则：

δ′(G)=min{|NG[e]|:e∈E(G)}=7

因此，对任意边e0，任意f∈F，满足：

(1)

下面对其中一个f进行分析。令E1为所有满足f(e)=-1的边，G1为E1在G=Cm×Cn中的导出子图，即G1=(V(G),E1)。下面分析导出子图G1的结构特征。

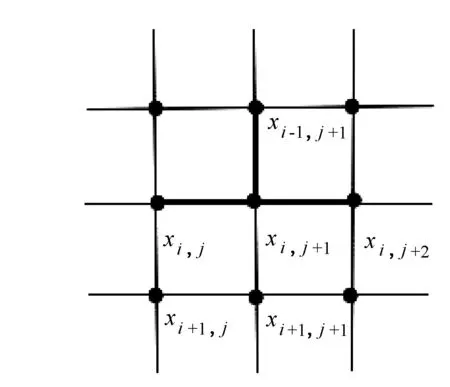
图1 断言2示意图

断言1G1不含度为4的顶点。

若含度为4的顶点，则对度为4的顶点关联的边e0而言有：

与式(1)矛盾。

断言2G1不含度为3的顶点，不含度为0的顶点。

根据对称性，不妨令xi,j+1为度为3的顶点，且该顶点在G1与顶点xi,j,xi,j+2和xi-1,j+1相邻(见图1)。由定义1知：

则xi+1,j+1为度为0的顶点，xi,j为度为1的顶点，从而xi+1,j为度为2的顶点。因此有：

与式(1)矛盾。

假设存在u为度为0的顶点，u与v在G中相邻，对边uv来说，由于：

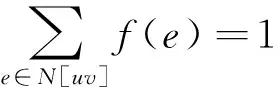
则v是度为3的顶点，矛盾。

断言3G1不含度为1的顶点。

设u为度为1的顶点，u与v在G1中相邻。根据断言1和断言2，v为度为1的顶点或者度为2的顶点，这样对边uv有：

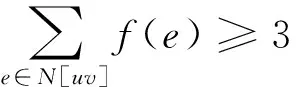
与式(1)矛盾。

综上，G1中所有顶点为度为2的顶点，从而G1为若干圈的并。令e0为非圈上边，则有：

与式(1)矛盾。故G1不存在，所以d≠7，结合引理1，定理1得证。

2 Cm×Cn的符号边domatic数下界

下面笔者通过构造符号边控制集给出Cm×Cn的符号边domatic数的下界，从而给出Cm×Cn的符号边domatic数的取值范围。

证明令:

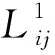
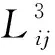
x2i,2jx2i+1,2j,x2i+1,2jx2i+2,2j,x2i+1,2j+1x2i+2,2j+1}

Ri={

x2i,0x2i,n-1,x2i+1,n-1x2i+2,n-1}

1)若m,n均为偶数，对t=1,2,3，构造函数ft：

2)若m+n为奇数，即m与n奇偶性相异。由于Cm×Cn≅Cn×Cm，不妨设m为偶数，n为奇数，构造f1,f2,f3如下：

3)若m,n均为奇数，构造f1,f2,f3如下：

上述3种情况的示意图分别如图2～图4所示。

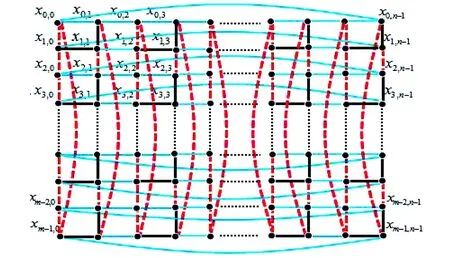
注：黑线、蓝线、红虚线分别代表f1,f2,f3取值-1，下同。图2 情形1)示意图

图3 情形2)示意图

图4 情形3)示意图

3 结语

考虑Cm×Cn的符号边domatic数，给出其取值上下界，得到其符号边domatic数为3 或者5，其确切符号边domatic数的确定是下一步研究的问题。

[参考文献]

[1]Bondy J A, Murty U S R.Graph theory with applications[M].London: Macmillan, 1976.

[2]Xu B.On signed edge domination numbers of graphs[J].Discrete Mathematics, 2001, 239(1-3): 179～189.

[3]Li X J, Xu J M.The signed edge-domatic number of a graph[J].Graphs and Combinatorics, 2013，29(6)：1881～1890.

[4]李金强，朱智博，成纯波，等.笛卡尔乘积图K2×Cn及C3×Cn的符号边domatic数[J].长江大学学报(自科版), 2015, 12(7): 8～10.