山地悬空管道地震作用下的动态响应分析
廖恒,雷震,徐晋东,杜国锋 (长江大学城市建设学院,湖北 荆州 434023)
管道是石油天然气输送的高效途径。20世纪以来,我国已经建成“西气东输”、“川气东送”以及跨国管道工程“中亚管道”、“中缅管道”等天然气长输管道工程,健全了我国复杂的管道系统输送网络。随着能源输送需求的进一步增大,对管道工程建设的需求也会进一步增加。我国幅员辽阔,管道工程难免会穿越地质灾害频发区,管道遭受地震破坏就会导致巨大的经济损失,因此对管道进行抗震研究显得尤为重要[1]。
目前关于埋地管道抗震分析和计算的研究成果较多[2~4],但是考虑地震作用下的悬空管道的研究还不够深入。刘志军[5]研究成果表明,在强震作用下悬空管道的位移反应和应力反应都比较大,管道的悬空长度是影响地震反应的关键因素;黄强兵等[6]认为,埋地管道在地震作用下的反应还与剪切波、管道的夹角、场地剪切波速、管径以及壁厚等因素有关;H.S.Choi[7]通过理论计算得到了悬空管道固有频率的表达式,表明了影响悬空管道固有频率的因素有管道的悬空长度、抗弯刚度、质量和两端的边界条件;郝婷玥等[8]根据Kelvin粘弹性地基模型将土壤的动力特性简化为阻尼器和理想弹塑性弹簧的整体组合,并建立管道的振动微分方程,利用数值解法,得到悬空管道各点的位移及加速度响应;国内学者冉龙飞等[9]、赵林等[10]对悬空长输管道有限元建模方法进行了研究;孙健[11]借助有限元软件对悬空管道进行了模态和地震响应分析,但这些研究中很少对管径等多参数下的悬空管道动力响应进行分析。为了研究山地悬空管道在地震作用下的动态响应,笔者利用有限元软件ABAQUS建立悬空管道有限元模型,并综合考虑了管道的悬空长度、管径和壁厚等因素对其受力性能的影响。
1 有限元模型的建立
ABAQUS包括可模拟任意几何形状的单元库,自动选择相应载荷增量和收敛限度,连续调节参数以保证在分析过程中有效地得到精确解,其附带的管土模型可以有效地进行地震响应分析[7]。为了简化模型,不考虑管内流体作用和管道外层保护层等因素的影响。模型取埋深为2m的钢管,土体模型的厚度和宽度取为10m,根据沉管作业过程中应力应变远程监测数据,管道沉降作业区两侧埋地端受影响区仅为悬空长度的0.4倍,设定土体长度为悬空长度的1/2[12]。土体采用的实体单元为8节点线性缩减单元(C3D8R)。悬空管道壁厚t较小,管道直径R较大,一般情况下((t/R)max≤1/10)属于薄壳,为保证管道单元在计算过程中不至于发生过度变形,综合考虑以上因素,管道采用三维4节点缩减壳单元(S4R),沿管道壁厚的方向设置5个积分节点。悬空管道的模型及网格划分如图1所示。
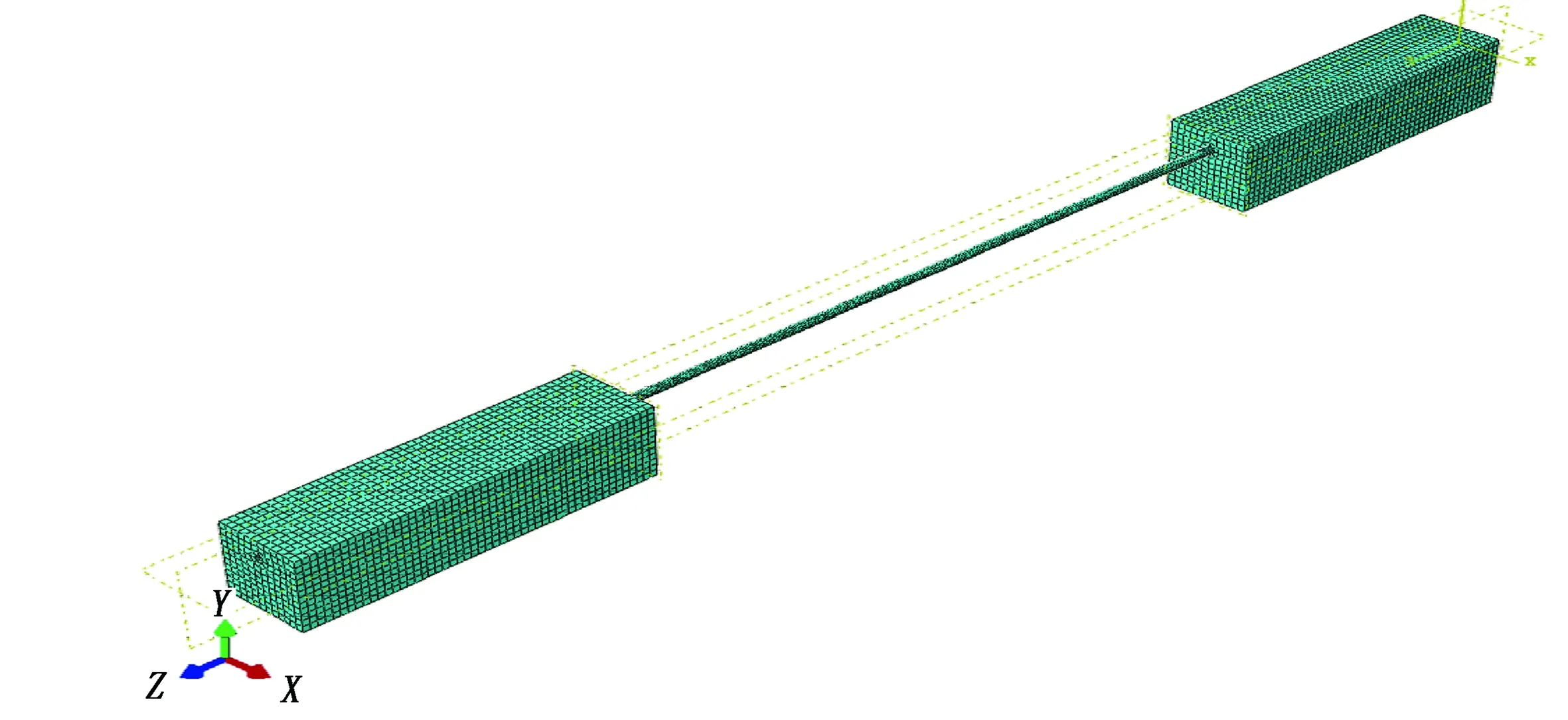
图1 悬空管道的模型及网格划分
模型中管道钢材选取X65钢[13],弹性模量为207GPa,管材密度为8010kg/m3,泊松比为0.3,屈服强度为450MPa。地基土为砂土,管土之间的摩擦系数为0.5[12],在软件中使用接触设置,管道的外表面作为第一表面,土体作为第二表面。土体材料参数取自文献[14],弹性模量为8MPa,重力密度为20.5kN/m3,泊松比为0.3,粘聚力为1kPa,内摩擦角为29°,剪胀角10°,结构阻尼比为0.05[15]。
2 悬空管道的模态分析
模态分析是动力学分析的基础和前提,结构和系统的振动特性决定了结构和系统对其他各种动力荷载的响应情况。利用有限元软件ABAQUS对山地悬空管道进行模态分析,在软件中定义一个线性摄动步的频率提取分析步,采用Lanczos法,设置振型为10阶。通过ABAQUS的模态分析后,得到管道的自振频率。
2.1 悬空长度对模态的影响

表1 管径1040mm、壁厚为10mm的不同悬空长度
表2悬空长度80m、管径1040mm不同壁厚管道的自振频率

振型不同管道壁厚下的自振频率/Hz8mm10mm12mm14mm1阶0.662050.662150.662560.662692阶0.662430.662540.664570.664883阶0.702540.699640.696420.693044阶0.713260.714230.715120.715915阶0.792720.785160.779780.775996阶0.831730.820940.811810.803877阶0.874130.878730.883170.887488阶0.891790.891840.891830.891789阶0.921380.927900.934410.9408210阶1.100201.134701.165201.19240
根据实际工程情况,悬空长度分别取40、60、80m,管径为1040mm、壁厚为10mm。利用有限元软件ABAQUS对模型进行模态分析,得到了不同悬空长度下管道前10阶模态的频率,如表1所示。
由表1可知,管道的悬空长度对管道的自振频率是有影响的,随着管道悬空长度的增加,管道的自振频率有降低的趋势。当管道的悬空长度一定时,管道的自振频率随模态阶数的增加而增大。
2.2 管道壁厚对模态的影响
用上述同样的方法,保持悬空长度为80m,管径为1040mm。得到了壁厚分别为8、10、12和14mm管道的前10阶模态的频率,如表2所示。
由表2可知,管道的壁厚对管道的自振频率是有影响的,随着管道壁厚的增加,管道的自振频率有增加的趋势。当管道的壁厚一定时,管道的自振频率随模态阶数的增加而增大。
2.3 管道直径对模态的影响
当悬空长度为80m,管道壁厚为10mm,可得到管径分别为440、640、840和1040mm管道的前10阶模态的频率,如表3所示。
由表3可知,管径对管道的自振频率是有影响的,随着管径的增加,管道的自振频率有增加的趋势。当管道的管径一定时,管道的自振频率随模态阶数的增加而增大。

表3 悬空长度80m、壁厚10mm不同直径管道
3 地震波的调整与选取
地震波根据地理位置的不同将具有很大的随机性。虽然难以预测管道所处的地理位置,但只要地震的主要参数正确,就可以较准确的模拟管道的受力状态,满足研究的精度要求。正确选择输入的地震波加速度时程曲线,要满足地震动三要素的要求,即频谱特性、有效峰值和持续时间。频谱特性依据所处的场地类别和设计地震分组确定;有效峰值按规范调整;持续时间取为4s,时间间隔取0.02s。在软件中以边界条件的形式在水平方向施加加速度时程曲线。
研究背景是山地悬空管道处于抗震设防烈度为7度(0.10g)、近源地震条件下的地区,该地区场地类别I1类,设计地震分组第1组,特征周期值0.25s。关于地震波的来源,PKPM软件根据特征周期对地震波分好了组。因此,从PKPM地震波库中,按照特征周期选取了4条波,根据多遇地震加速度时程最大值35cm/s2对地震波峰值进行调整。地震波的时程曲线如图2~图5所示。

图2 RH1TG025地震波时程曲线 图3 RH2TG025地震波时程曲线

图4 TH3TG025地震波时程曲线 图5 TH4TG025地震波时程曲线
利用Midas地震数据生成器SGS,将地震波时程曲线生成地震波的加速度谱,并与规范加速度谱进行对比和选择,如图6所示。

图6 地震波生成反应谱
在以往的研究中,许多学者认为只有基频才会对管道的振动产生较大的影响。但为了充分的考虑到高阶频率对管道振动的影响,根据对悬空管道的模态分析,可以发现前10阶模态的自振周期大致在0.7~1.5s,在该时间区间选取与规范反应谱最接近的地震波数据。由图6可知,RH1TG025地震波和RH2TG025地震波比较符合,但RH1TG025地震波在前部分与规范反应谱的拟合程度比RH2TG025地震波更高,且RH2TG025地震波反应谱的平台部分低于规范反应谱,为了保守起见和综合以上分析最终选择RH1TG025地震波用于山地悬空管道的动态响应分析。
4 数值模拟与分析
利用有限元软件ABAQUS把地震波的加速度时程曲线输入到悬空管道模型上,通过软件计算的结果来分析和研究不同管径、悬空长度和壁厚的管道在地震作用下的应力和位移响应。
4.1 不同悬空长度下管径对管道动态响应的影响
不同悬空长度下管径对管道动态响应如图7~图12所示。由图7~图12可知,对于悬空长度是40、60、80m的管道,当悬空长度和壁厚一定时,管道的应力随着管道直径的增大而减小。这是因为管径的增加也使得管道的抗弯刚度增大,而且管径对管道的抗弯刚度影响是显著的,这一点从模态分析中也可以看出,即随着管径的增大管道的自振频率也显著增大,管道的位移亦是如此。在沿着管道纵向方向上,悬空段的跨中和非悬空段的约束中部的应力最大,内外出土端的应力较小。悬空段的跨中竖向位移最大。而且管道的悬空长度对应力和位移影响也是显著的,管道的应力和位移随着悬空长度的增大而增加。

图7 悬空长度40m管道不同管径的应力分布 图8 悬空长度40m管道不同管径的竖向位移分布
4.2 不同悬空长度下壁厚对管道动态响应的影响
不同悬空长度下壁厚对管道动态响应如图13~图18所示。由图13~图18可知,对于悬空长度是40、60、80m的管道 ,当悬空长度和管径一定时,非悬空段的管道应力随着管道壁厚的增大而减小,这一结论与文献[3]相同。相反的是,悬空段的管道应力随着管道壁厚的增大而增大,通过模态分析可知,随着管道壁厚的增加,管道的自振频率在增大,说明管道的抗弯刚度相对于管道的质量是增大的。但在地震作用下,结构刚度加大,地震作用同时也会加大,因此在悬空段会出现这种现象。从具体的数据可知,管道的应力和竖向位移的数值变化幅度并不大,因此壁厚对管道的动态响应影响并不是很大,悬空长度对管道的影响显著。

图9 悬空长度60m管道不同管径的应力分布 图10 悬空长度60m管道不同管径的竖向位移分布

图11 悬空长度80m管道不同管径的应力分布 图12 悬空长度80m管道不同管径的竖向位移分布

图13 悬空长度40m管道不同壁厚的应力分布 图14 悬空长度40m管道不同壁厚的竖向位移分布
5 结论
1)通过对管道的模态分析,管道相邻振型的自振频率相差不大。
2)在地震作用下,山地悬空管道随着悬空长度的增加,管道的应力及位移都会显著的增大,说明管道的悬空长度对管道的地震动态响应有显著的影响,在实际工程中应尽可能减小悬空长度。
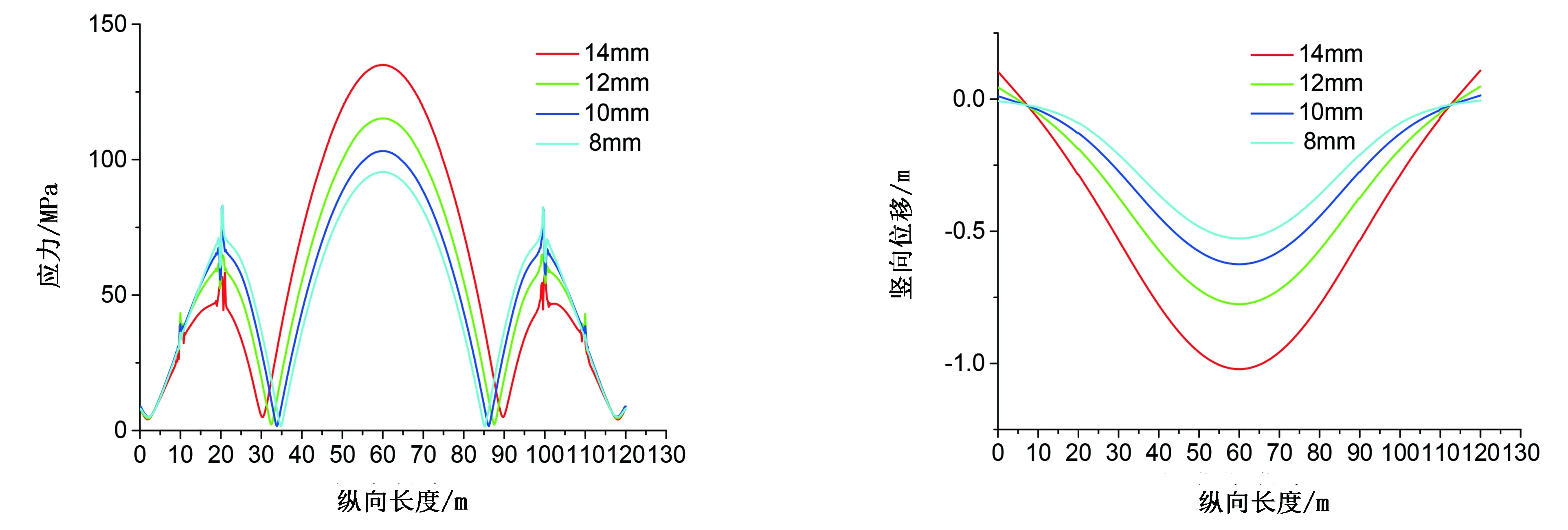
图15 悬空长度60m管道不同壁厚的应力分布 图16 悬空长度60m管道不同壁厚的竖向位移分布
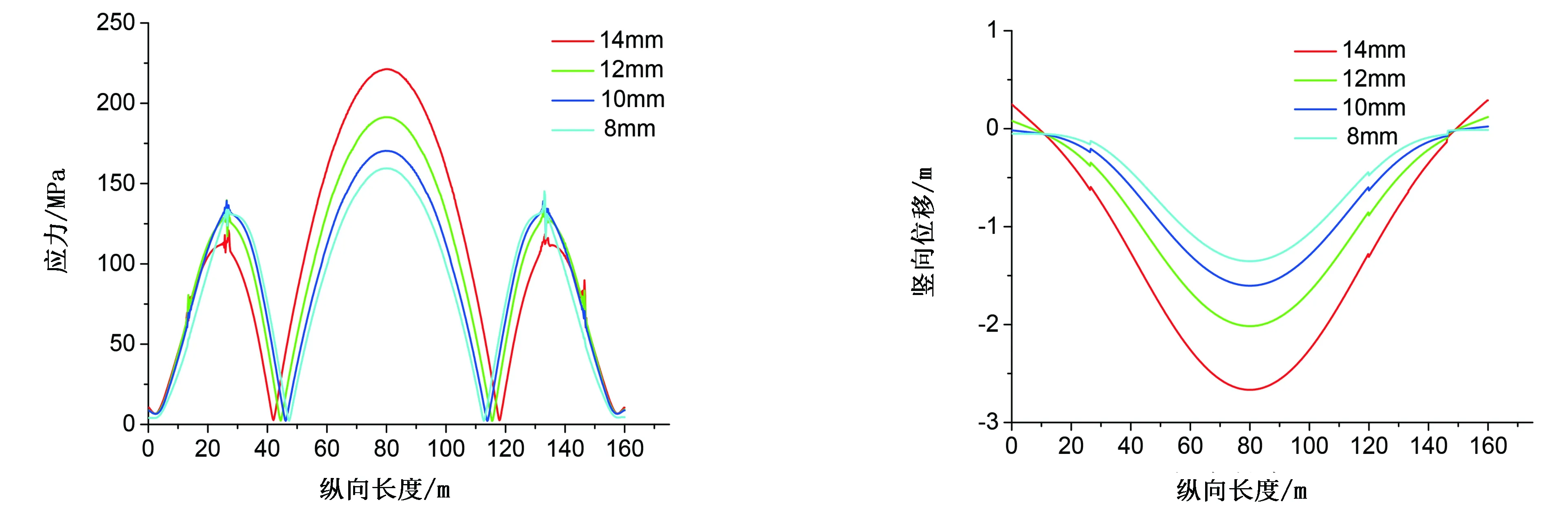
图17 悬空长度80m管道不同壁厚的应力分布 图18 悬空长度80m管道不同壁厚的竖向位移分布
3)随着管径的增加,悬空管道的应力及竖向位移都会显著的减小,大管径有利于减弱管道的动态响应。
4)壁厚对管道的动态响应有一定的影响,但影响的幅度并不大。
5)管道的应力峰值多集中在悬空区的跨中部位和非悬空区的有效约束中间部位,可以采取减震措施,使用补偿器,增加阻尼,提高其抗震性能。
[参考文献]
[1]张陵,郭惠勇,孙清,等.长输管道抗震研究的进展与趋向[J].西安交通大学学报,2001,35(02):203~209.
[2] 刘红丽.长输油气管线工程抗震综合研究[D].哈尔滨:中国地震局工程力学研究所,2004.
[3] 薛景宏,逯广东,李井水. 埋地管道动力反应时程分析结果与规范比较[J]. 油气田地面工程,2005,24(11):11~24.
[4] 赵新威,曾祥国,姚安林,等. 地震载荷作用下埋地输气管道的数值模拟[J]. 石油机械,2014,42(3):104~109.
[5] 刘志军,倪立峰,周星德,等.悬垂管道跨越结构地震反应分析[J].地震工程与工程振动,2004,24(5):123~126.
[6] 黄强兵,彭建兵,杨天亮.埋地管道在地震波作用下的抗震性能分析[J].工程勘察,2004(3):64~67.
[7] Choi H S.Free spanning analysis of offshore pipelines[J].Ocean Engineering,2001,28(10):1325~1338.
[8] 郝婷玥,陈贵清,马卫华.地震作用下埋地管道横向振动分析[J].四川建筑科学研究,2010,36(2):204~207.
[9] 冉龙飞,王晓霖.埋地悬空管道的安全评估影响因素研究[J].化工设备与管道,2016,53(6):81~ 86.
[10] 赵林,冯启民.埋地管线有限元建模方法研究[J].地震工程与工程振动,2001,21(2):53~57.
[11] 孙健.基于ABAQUS的悬空管道地震响应分析[J].石油和化工设备,2014,17(7):30~33.
[12] 武立伟.埋地管道极限悬空长度研究[D].西安:西安石油大学,2015.
[13] 高圣平.管线钢管规范[M].第45版.王慧.北京:石油工业标准化研究所,2012.
[14] 崔春义,孟坤,梁志孟,等.深圳老街地铁车站自由场地地震动力特性数值分析[J].沈阳建筑大学学报(自然科学版),2016,32(6):1008~1016.
[15] 黄宗明,白绍良,赖明.结构地震反应时程分析中的阻尼问题评述[J].地震工程与工程振动,1996(2):95~105.

