单、双层套管-地层完备系统应力变化规律研究

许福东，董立，谭超 (长江大学机械工程学院，湖北 荆州 434023)

随着石油工业的发展，深井、超深井、复杂结构井数量越来越多，套损变形破坏越来越多。套管的损失变形不仅影响油气井的钻采作业，而且造成巨大的经济损失。对于油气井中固井后围岩外挤载荷导致套管损坏已有大量的研究[1～7]，这些研究大多将套管-水泥环-地层作为独立体进行分析，但将其作为整体系统进行考虑和对比分析不多见。为了更加明确多种油气井井身套管结构的受力状况，具体探讨单、双层套管-地层完备系统之间的相互受力情况，笔者运用弹性力学知识，建立了单、双层套管-地层完备系统简化力学模型，并作应力计算,对其应力变化规律进行了对比分析。

1 单、双层套管-地层完备系统简化力学模型

单、双层套管-地层完备系统是指石油钻井过程中使用水泥固井后，水泥固井质量良好，套管无损坏，水泥环不发生开裂，系统各层之间连接紧密，没有相对滑动，交界处径向位移和应力连续的系统[8～11]。对该系统的基本要求和实际条件分析，系统的力学性能研究可简化为平面应变轴对称应力问题[12～15]。单、双层套管-地层完备系统简化力学模型如图1所示，其中双层套管中间环包含水泥-地层完备系统和液体-地层完备系统2种情形。

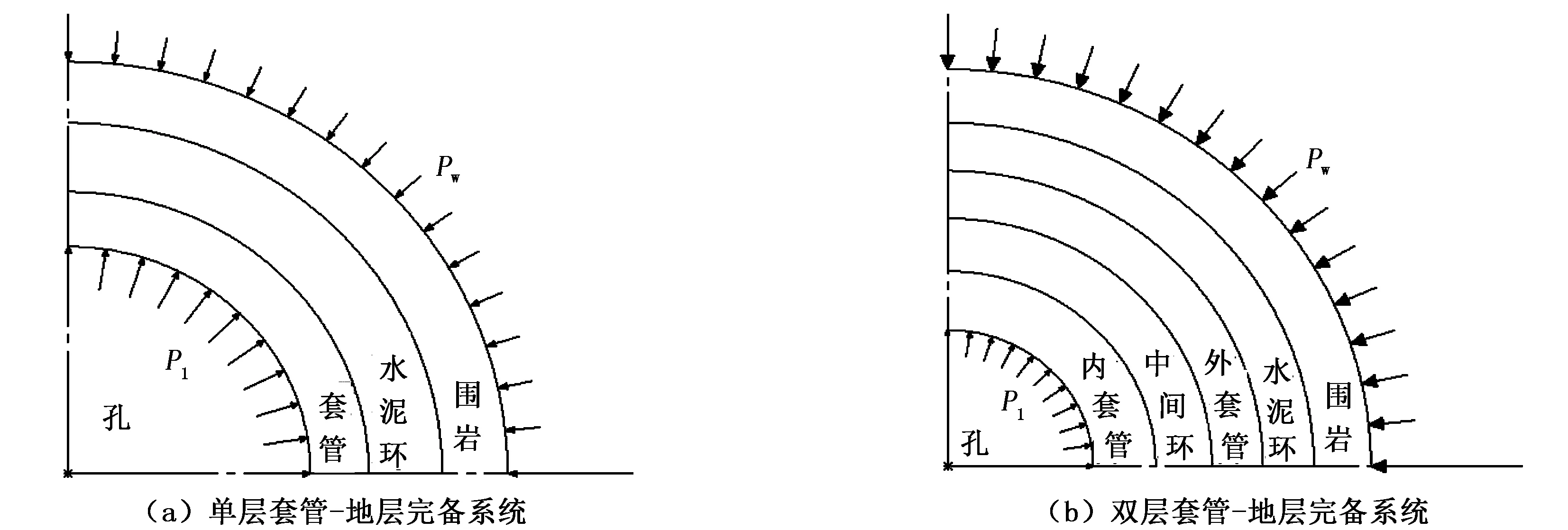
图1 单、双层套管-地层完备系统力学模型

2 套管-地层完备系统轴对称应力分析

设套管受内压力为P1，地层边界作用围压为Pw；套管弹性模量为E1，泊松比为μ1；水泥环弹性模量为E2，泊松比为μ2；地层岩石弹性模量为E3，泊松比为μ3。其中，双层套管中间环为液体-地层完备系统中间环，液体为非腐蚀性不可压缩液体。

套管-地层完备系统可简化为平面应变轴对称应力问题。在轴对称应力状态下，应力函数Φ是标量函数，且只是ρ的函数：

Φ=Φ(ρ)

(1)

在这一特殊情况下，应力公式可以简化为：

(2)

式中，σρ与σφ分别为径向应力与周向应力；τρφ和τφρ为切应力。

相容方程式简化为：

(3)

轴对称问题的拉普拉斯算子可以写为：

(4)

代入相容方程可得：

(5)

式(5)积分4次就得到轴对称应力状态下应力函数的通解：

Φ=Alnρ+Bρ2lnρ+Cρ2+D

(6)

式中，A、B、C、D是待定的常数。

将应力函数代入应力公式，得轴对称应力的一般性解：

(7)

(8)

(9)

将形变分量代入几何方程可得到轴对称应力下对应的径向位移分量：

+Icosφ+Ksinφ

(10)

(11)

(12)

周向应力一般性通解为：

(13)

2.1 单层套管-地层完备系统

对于套管内壁，应力边界条件为：

(σ1ρ)ρ=R1=-P1

(14)

对于套管外壁与水泥环内壁，应力边界条件和位移边界条件为：

(σ1ρ)ρ=R2=(σ2ρ)ρ=R2

(15)

(U1ρ)ρ=R2=(U2ρ)ρ=R2

(16)

对于水泥环外壁与围岩内壁，应力边界条件和位移边界条件为：

(σ2ρ)ρ=R3=(σ3ρ)ρ=R3

5) 用于紧急切断阀及现场操作开关的电缆应采取防火保护措施或采用防火电缆，保护控制信号的传输在发生火灾初期不会立即中断，确保发生火灾时能及时切断紧急切断阀。

(17)

(U2ρ)ρ=R3=(U3ρ)ρ=R3

(18)

对于围岩外壁，应力边界条件为：

(σ3ρ)ρ=R4=-Pw

(19)

将式(14)～(19)代入式(11)～(13)，可以求得对应的应力函数的待定系数。

2.2 双层套管中间环为水泥-地层完备系统

双层套管中间环为水泥-地层完备系统对应的边界条件如表1所示。

表1 双层套管中间环为水泥-地层完备系统对应边界条件

将边界条件分别代入式(11)～(13)，可求得对应的应力函数的待定系数。

2.3 双层套管中间环为液体-地层完备系统

双层套管中间环为液体-地层完备系统对应的边界条件如表2所示。

表2 双层套管中间环为液体-地层完备系统对应边界条件

对于内套管外壁与外套管内壁，除应力边界条件外，内套管的变形量与外套管的变形量也相同，即：

ΔV内=ΔV外

也即：

(20)

将边界条件分别代入式(11)～(13)，并与式(20)联立可求得对应的应力函数的待定系数。

3 现场实例计算

表3为华北油田某井场地层 、水泥以及套管的现场井身结构参数和相应外载荷参数值。代入表3中的具体参数进行计算可得套管-地层完备系统中同一截面的径向和周向应力分布，如图2～图4所示。

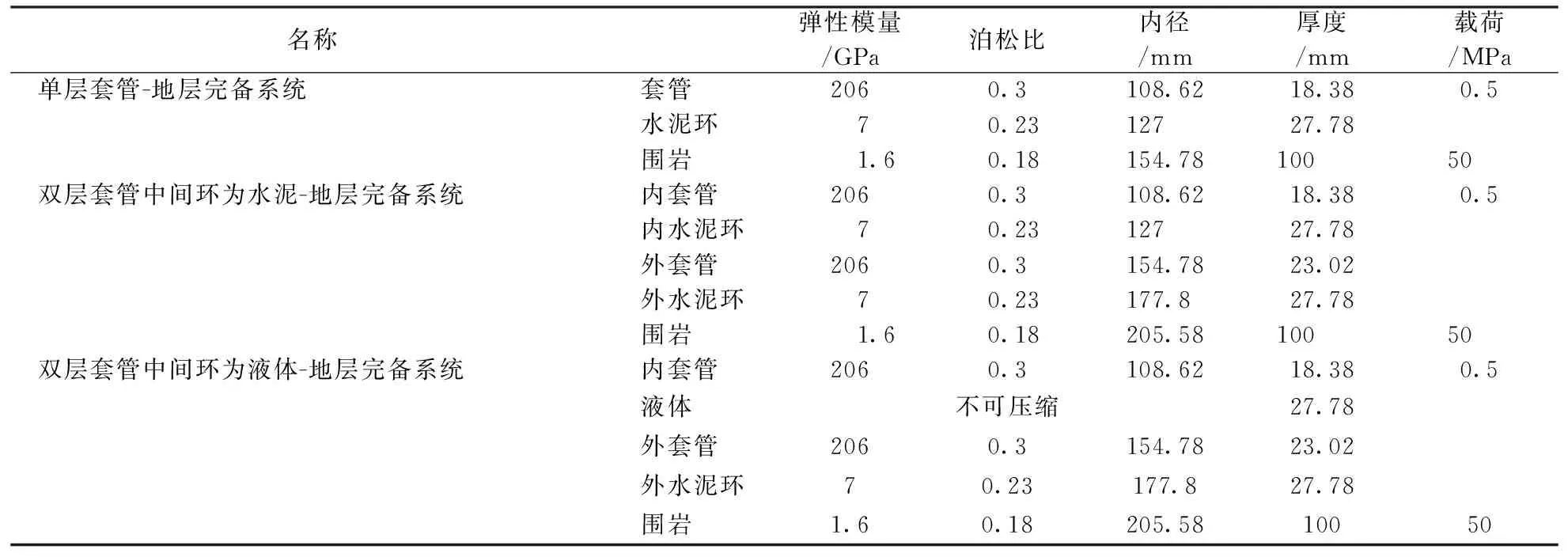
表3 套管-水泥环-地层完备系统井身结构参数

表4 Matlab求解待定系数结果

图2 单层套管-地层完备系统的径向应力和周向应力分布图

3.1 单、双层套管-地层完备系统应力分布规律

单层套管-地层完备系统中径向应力最大处位于套管和水泥环交界处。双层套管中间环为水泥-地层完备系统中径向应力最大处位于外层套管和外层水泥环交界处。双层套管中间环为液体-地层完备系统中径向应力最大处位于外层套管和外层水泥环交界处。

3种系统中随着半径增大，套管径向应力增大，而水泥环和围岩反之，且其径向应力分布是连续的，但周向应力均为不连续,外层套管周向应力大于内层套管周向应力。

3.2 单、双层套管-地层完备系统应力分布结果对比分析

对比图2和图3可以发现，单、双层套管-地层完备系统的应力分布中，各部分应力均发生显著变化，并且各个接触面上径向应力连续，周向应力不连续。但是双层套管的最大径向应力和周向应力要比单层套管的小很多。对比图3和图4可以发现，对于双层套管中间环为液体-地层完备系统和双层套管中间环为水泥-地层完备系统，内层套管的径向应力变化趋势明显较缓，即对内层套管的失效有明显的缓解作用，地层压力传到内层套管外壁的压力大大减小。

图3 双层套管中间环为水泥-地层完备系统的径向应力和周向应力分布图

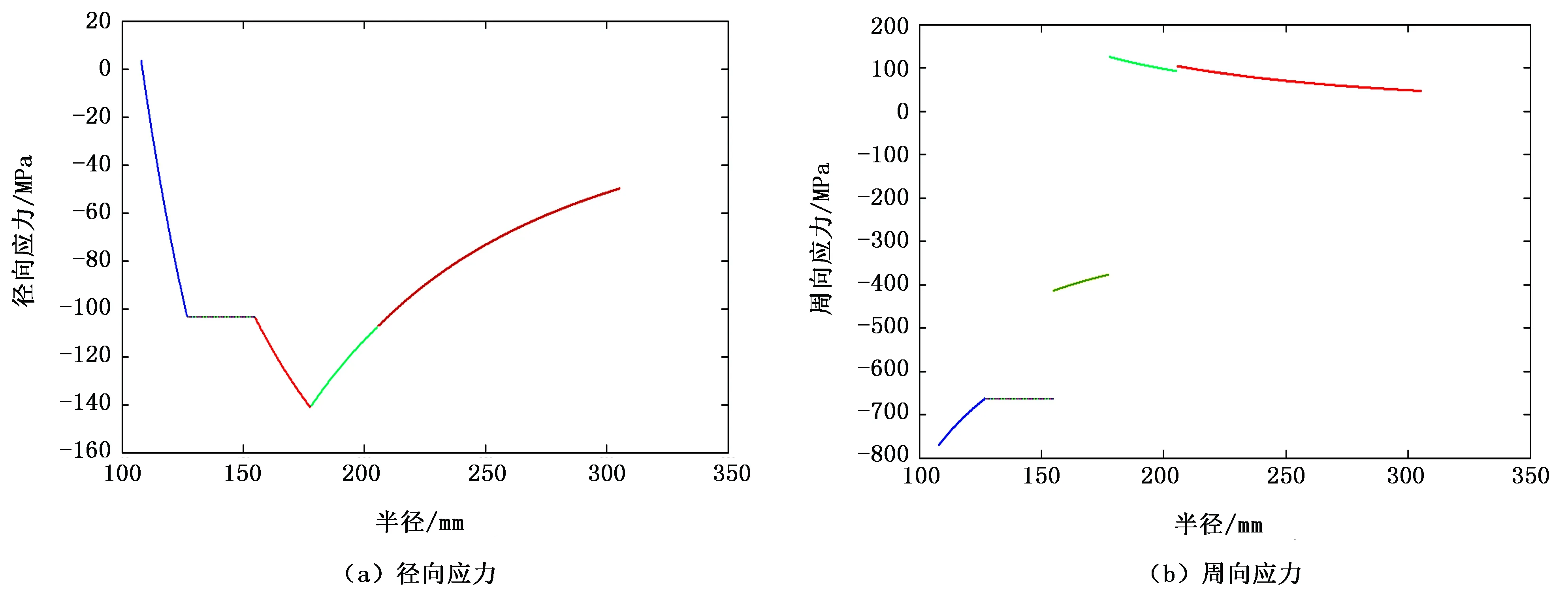
图4 双层套管中间环为液体-地层完备系统的径向应力和周向应力分布图

4 结论

1)建立了单、双层套管-地层完备系统的简化力学模型，并且计算了其径向应力和周向应力，绘制了套管-地层完备系统的应力分布图，对分布结果进行了分析对比。

2)双层套管的最大径向应力和周向应力要比单层套管的小很多，说明双层套管能有效地保护套管、井壁的损失变形破坏。

3)相对于中间环为水泥的套管-地层完备系统，中间环为液体的套管-地层完备系统外层套管内表面和内层套管外表面的受力更加均匀。双层套管中间环为液体-地层完备系统抗挤强度大于中间环为水泥的双层套管的抗挤强度，相对于其他2种系统，有更优地防套变作用。

4)以上这些研究和发现为预防油田开发中大量套变、合理地进行井身套管结构强度设计提供了有力的理论依据。

[参考文献]

[1]李军,李贵川,陈勉，等.双层组合套管设计计算中径向位移公式的确定[J].石油天然气学报(江汉石油学院学报),2005,27(4):517～518.

[2]梅超超.地层和水泥环耦合条件下套管内应力分布研究[D].成都：西南石油大学,2014.

[3]张景富,张德兵,张强,等. 水泥环弹性参数对套管-水泥环-地层固结体结构完整性的影响[J]. 石油钻采工艺,2013,35(5):43～46.

[4]胡光辉. 定向井固井水泥环应力分布研究[D].成都：西南石油大学,2014.

[5]李若莹,谢亚雄,梅超超. 水泥环对套管应力影响的模拟与分析[J]. 石油化工应用,2014,33(10):30～33,39.

[6] Wang Zijian, Wu Liming, Xiong Huan.Analysis of Mechanical Property of Taniguchi Bridges in Mountainous Areas Loaded by Fluctuating Wind[J]. Applied Mechanics and Materials,2011,71～78:3543～3547.

[7]Fan M H，Jiao Y S，Cai Z X.An Analytical Solution for Stress and Displacement in Casing-Cement Combined Cylinder under Non-Uniform Loading[J].Advanced Materials Research,2011,291～294:2133～2138.

[8] 徐芝纶.弹性力学简明教程[M].北京：高等教育出版社,2002.

[9]王宴滨,高德利,房军. 套管-水泥环-地层多层组合系统受力特性分析[J]. 应用力学学报,2014,31(3):387～392,490.

[10]李军,陈勉,柳贡慧,等.套管、水泥环及井壁围岩组合体的弹塑性分析[J]. 石油学报,2005,26(6):99～103.

[11] 赵新波,韩生超,杨秀娟,等. 热固耦合作用下的套管-水泥环-地层多层组合系统应力分析[J]. 中南大学学报(自然科学版),2017,48(3):837～843.

[12]殷有泉,陈朝伟,李平恩. 套管-水泥环-地层应力分布的理论解[J]. 力学学报,2006, 38(6):835～842.

[13]陈朝伟,蔡永恩. 套管-地层系统套管载荷的弹塑性理论分析[J]. 石油勘探与开发,2009,36(2):242～246.

[14]练章华,赵国珍,董范,等. 双层组合套管内填充液体介质的力学分析[J]. 石油钻采工艺,1997,19(5):1～5，111.

[15]王耀锋,李军强,杨小辉. 套管-水泥环-地层系统应力分布规律研究[J]. 石油钻探技术,2008,36(5):7～11.