基于改进遗传算法的大坝参数快速反演工具研究及应用

孙辅庭，张秀丽，王玉洁，沈海尧

(1.国家能源局大坝安全监察中心，浙江杭州311122；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州311122)

0 引 言

获取大坝和坝基的真实力学参数对运行期大坝变形预测、应力控制、工作性态评估而言至关重要。现阶段，获取大坝真实力学参数最有效的方法是通过大坝监测资料结合计算反演得到大坝和坝基的综合参数，该方法类似于对大坝进行1∶1的模型试验[1]。

在大坝参数反演分析研究方面，国内外学者已经做了深入的研究工作。吴相豪[2]、李守巨[3]、Ardito[4]等学者采用单纯形法、最小二乘等传统方法进行大坝参数反演研究。近年来，学者们将智能优化方法与参数反演问题相结合进行了大量研究。Yang[5]对人工鱼群算法在大坝参数反演中的应用开展了研究；练继建等[6]基于BP神经网络对李家峡拱坝材料参数进行了研究；李端有等[7]将均匀设计理论、BP神经网络和遗传算法三者结合进行大坝力学参数的智能反演；徐宝松等[8]基于粒子群算法对陈村大坝的坝体混凝土弹性模量进行反演计算；宋志宇等[9]研究了混沌人工鱼群算法在重力坝材料参数反演中的应用；董威信等[10]采用人工神经网络反演了糯扎渡堆石坝的力学参数。此外，其他学者也在大坝参数反演方面也进行了大量的研究[11-13]。

尽管大坝参数的反演方法研究成果众多，但高效反演工具的研究成果较少。鉴于此，本文利用ANSYS软件以APDL[14]编程语言进行二次开发，将改进遗传算法强大的优化搜索能力和ANSYS软件本身强大的前后处理和计算能力相结合，开发大坝力学参数快速反演工具。

1 遗传算法的改进

1.1 遗传算法

遗传算法(Genetic Algorithm，GA)是由美国的Holland教授[15]于1975年首先提出的一类借鉴生物优胜劣汰的繁殖思想进行随机搜索的智能优化算法。遗传算法优化搜索过程中，解变量对于待定结果的满足程度通过适应度函数判断，监测点i的适应度函数Fi为

(1)

式中，δi_cal为计算效应量；δi_mea为真实效应量。效应量可以是变形、应力、水头、温度等。

遗传算法优化过程中，正是根据适应度函数的大小对求解结果的优劣进行判断，由此决定个体遗传概率以及计算是否终止。然而，传统遗传算法搜索过程中往往会出现早熟(遗传算法初期个别优势个体导致的局部收敛)和停滞(遗传算法后期个体差别小导致的搜索停滞)现象，因此需要对遗传算法进行改造以提高其搜索效率。

1.2 算法改进

参考模拟退火算法以及文献[16]的做法，引入幂函数缩放函数对适应度函数进行重构，重构的新适应度函数f为

(2)

式中，T为缩放系数，类似于模拟退火算法中的温度,T=α·βNG,α、β为常参数，NG为遗传代数。

以缩放处理后新的f替代F作为适应度评价以及繁殖概率选择的依据。改进后，可实现遗传算法初期对适应度值进行压缩而避免早熟，遗传算法后期对适应度值进行拉伸而避免搜索停滞。

2 大坝参数快速反演工具的开发

2.1 参数快速反演工具开发

将大坝监测资料分析、有限元计算以及改进GA相结合，形成一套大坝参数快速反演程序，其基本流程如图1所示。

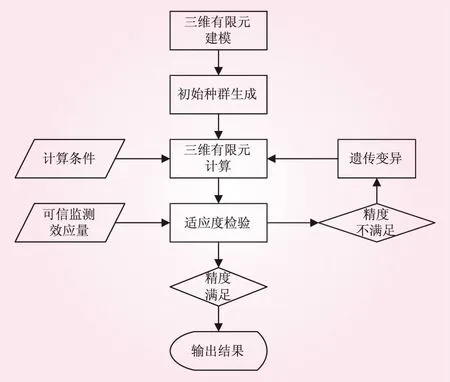
图1 基于GA的大坝参数快速反演流程

根据快速反演流程，ANSYS软件平台下基于改进GA的大坝参数反演基本步骤为：①建立研究对象的三维有限元模型；②根据待定参数范围生成初始种群；③根据输入计算条件进行有限元分析；④根据实测值和计算值进行适应度函数检验。精度满足要求则转步骤⑤，精度不满足，则进入遗传优化模块，并转步骤③；⑤输出大坝参数反演优化结果。

ANSYS自带的参数化编程语言APDL能够对软件进行二次开发，扩充分析功能，从而完成复杂分析过程。利用APDL的宏功能编制相应的程序实现反演流程中不同功能模块化，最后通过主程序调用宏模块实现整个优化计算过程。

2.2 程序验证

为验证反演工具的正确性，通过简单的拱坝参数反演算例进行验证。算例的目的仅仅是验证反演工具的正确性，因此作为反演条件输入的实测信息由有限元正分析结果代替。遗传算法参数设定如下：初始种群数量NP取20，杂交概率p取0.6，变异概率pm取0.05，幂函数缩放参数α取0.3，β取1.2，最大迭代次数NG设为20，迭代终止条件为考察点变形误差均方根低于0.1%。

算例拱坝最大坝高约230 m，有限元模型采用八节点六面体等参单元剖分，见图2。反演计算选取两种水位状态，状态1上游水深227 m，状态2上游水深207 m。反演计算给定混凝土弹性模量初始区间[10，50]GPa，坝基岩体变形模量初始区间[10，40]GPa。图3为拱坝参数反演计算过程中检验点变形输入值和反演优化值之间误差均方根的收敛过程，表1为反演优化得到的变形参数结果。

就参数反演结果而言，对于本次研究的简单拱坝算例，传统的基本遗传算法以及采用本文改进的遗传算法均能计算得到较为精确的变形参数，但改进算法的计算精度相对更高。由此可知，本文开发的参数反演工具是正确的，并且经改进的遗传算法较传统算法能搜索到更为精确的结果。

图2 有限元模型及检验点位置

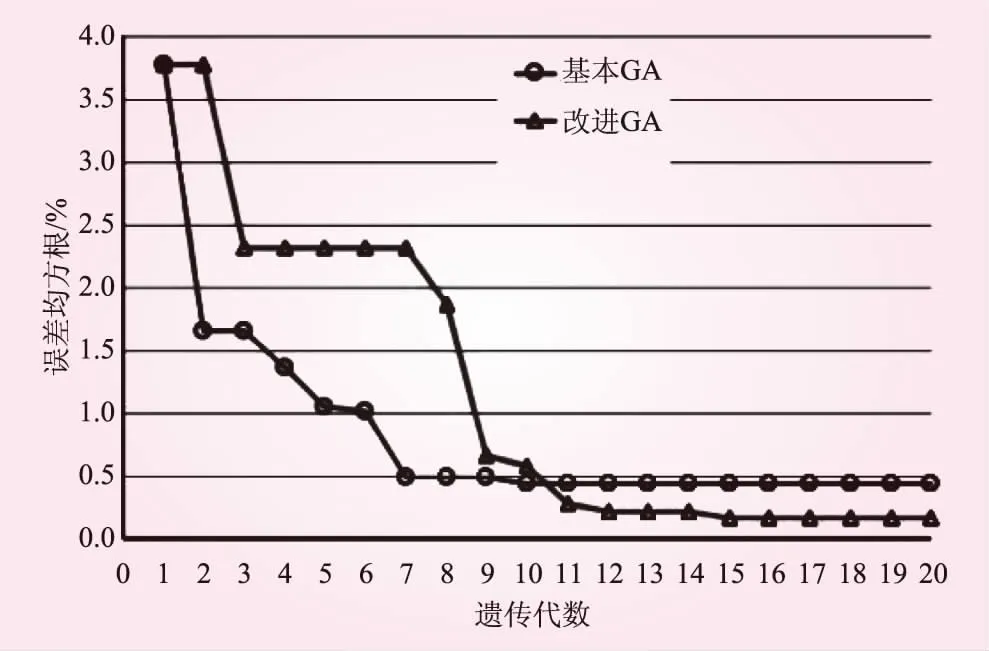
图3 检验点变形误差收敛趋势

GPa

3 工程应用

某水电枢纽工程位于四川省，拦河坝为300 m级特高混凝土拱坝，工程自首次蓄水至正常蓄水位以来，已正常运行超过2年，以下采用开发的工具对拱坝真实变形参数进行反演计算。模型主要模拟混凝土拱坝及地质构造。模型采用8节点等参单元剖分，共剖分单元总数221 194，节点总数239 448。

反演计算选取水位明显变动期(2016年6月～2016年9月)作为计算时段，以水荷载增量和温度荷载增量作为计算荷载，其中混凝土温度线膨胀系数由坝体埋设的无应力计监测值反算得到。以坝体垂线监测的水平位移增量作为检验效应量，拱坝变形检验点位置如图4所示。

图4 计算变形检验点示意

参数优化初始取值过程中，混凝土弹性模量初始计算区间由大直径芯样(290 mm)试验均值确定，岩体变形模量初始计算区间由地勘建议均值确定。表2为反演得到的混凝土及岩体真实变形参数。

表2 拱坝变形参数反演结果 GPa

进一步将计算检验点的实测变形和计算变形值列于表3。就整体而言，反演优化计算得到的拱坝变形增量与实测值较为接近，因而反演得到的变形参数基本能够反演拱坝真实工作性态。

表3 检验点变形结果 cm

4 结 论

基于运行期获取大坝真实力学参数的需求，在大坝参数快速反演工具的研究和应用方面开展相应工作。主要研究内容和结论如下：

(1)针对传统GA存在的搜索效率问题，引入缩放函数重新构造适应度函数，改善了算法存在的早熟和搜索停滞问题，提高了算法效率。

(2)构建了基于有限元法和改进GA的大坝参数快速反演流程，基于ANSYS软件以APDL参数化编程语言为工具，开发了大坝参数快速反演工具，并通过算例验证了程序的正确性。

(3)利用反演工具对某高混凝土拱坝的变形参数进行反演计算，分析结果表明，大坝参数反演工具能够较好地解决拱坝参数反演问题。

参考文献：

[1] 顾冲时, 吴中如. 综论大坝原型反分析及其应用[J]. 中国工程科学, 2001, 3(8)： 76- 81．

[2] 吴相豪, 吴中如, 顾冲时, 等. 碾压混凝土拱坝徐变度反演分析方法[J]. 大坝观测与土工测试, 2000, 24(1)： 22- 24．

[3] 李守巨, 刘迎曦, 王登刚, 等. 混凝土重力坝材料参数识别的正则化最小二乘法[J]. 计算物理, 2000, 17(6)： 702- 706．

[4] ARDITO R, BARTALOTTA P, CERIAN L. Diagnostic inverse analysis of concrete dams with statical excitation[J]. Journal of the Mechanical Behavior of Materials, 2004, 15(6): 381- 389．

[5] YANG G, LIU H Z, ZHU K, et al. The inversion analysis for mechanical parameters of dam based on the artificial fish swarm algorithm[J]. Applied Mechanics and Materials, 2013, 416- 417: 1786- 1790．

[6] 练继建, 王春涛, 赵寿昌. 基于BP神经网络的李家峡拱坝材料参数反演[J]. 水力发电学报, 2004, 23(2)： 44- 48．

[7] 李端有, 甘孝清, 周武. 基于均匀设计及遗传神经网络的大坝力学参数反分析方法[J]. 岩土工程学报, 2007, 29(1)： 125- 130．

[8] 徐宝松, 苗艳东, 李波, 等. 基于粒子群算法的大坝力学参数反演[J]. 水力发电, 2009, 35(3)： 102- 104．

[9] 宋志宇, 李俊杰, 汪红宇. 混沌人工鱼群算法在重力坝材料参数反演中的应用[J]. 岩土力学, 2007, 28(10)： 2193- 2196．

[10] 董威信, 袁会娜, 徐文杰, 等. 糯扎渡高心墙堆石坝模型参数动态反演方法[J]. 水力发电学报, 2012, 31(5)： 203- 208．

[11] 李业成, 刘昉, 马斌, 等. 基于改进HHT的高拱坝模态参数识别方法研究[J]. 水力发电学报, 2012, 31(1)： 48- 55．

[12] 雷朋, 苏怀智, 张贵金. 基于RNN模型的坝体和岩基区间参数反演方法研究[J]. 岩土力学, 2011, 32(2)： 547- 552．

[13] 余祥荣, 张社荣, 王雪红, 等. 基于果蝇-BP神经网络算法的大坝力学参数反演[J]. 水利水电技术, 2014, 45(9)： 52- 54．

[14] 龚曙光, 谢桂兰, 黄云清. ANSYS参数化编程与命令手册[M]. 北京： 机械工业出版社, 2009．

[15] HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. 2nd ed. Cambridge: MIT Press, 1992．

[16] 刘云峰, 曹春蕾. 一维大地电磁测深的遗传算法反演[J]. 浙江大学学报： 自然科学版, 1997, 31(3)： 300- 304．