基于PFC2D的岸坡覆盖层失稳堵江模拟研究

李子隆，许 模，赵 勇，王子忠，郭 健，李明月

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都610059；2.四川省水利水电勘测设计研究院，四川成都610072)

0 引 言

随着人类对水资源需求的不断增加，水利水电工程的数量也逐渐增长，库岸边坡的安全问题更不容忽视。库岸边坡的失稳会带来严重的灾难，大量的岩土体进入水库产生涌浪(如Vaiont水库)，岩土体堆积造成堵江并形成堰塞湖，对人类的生存环境造成严重威胁。目前，对边坡稳定性的研究方法层出不穷，数值模拟软件各式各样，但对滑坡失稳后造成堵江的研究通常都是采用经验法[1-2]，相关研究软件也相对较少，最常用的方法是用FLAC3D分析边坡的稳定性及变形特征，再用UDEC模拟边坡的破坏特征并预测堰塞坝高度[3- 4]。徐文杰对肖家河滑坡稳定性做了分析，并用ABAQUS/Explicit动力有限元分析滑坡在地震工况下的堵江过程[5]。有限元模拟的块体不能破裂，模拟效果并不明显。学者们对于土质边坡的模拟大多采用离散元颗粒流程序PFC。宋朋燃考虑了降雨的因素，用PFC3D模拟了黄土滑坡坡面冲刷破坏过程[6]；马建全用PFC2D模拟了黑方台滑坡各破坏阶段的变形特征；周健建立了粘性土坡和砂性土坡的理想模型，分析了微观参数对斜坡变形的影响，随着参数的增加，变形由塑性转变为脆性[7]；梁承洋用PFC2D模拟了川藏交通廊道冰碛物滑坡堵江堆积物的形态，同时研究了单因素变量对堵江的影响[8]。

地下水是库岸边坡失稳的最重要因素，很多欠稳定的斜坡在地下水位升高后覆盖层失稳，并造成堵江，但对于考虑地下水位的边坡堵江研究并不多。为此，本文采用PFC2D颗粒流程序，建立有覆盖层的库岸边坡模型，采用降低微观参数的方法模拟不同的地下水位，并研究其破坏过程和堵江坝高预测，分析库岸边坡覆盖层饱和土体比例与堵江形成堰塞坝高度之间的关系。

1 颗粒流PFC理论

1.1 基本假设

PFC2D是基于离散单元法的颗粒流程序软件，通过颗粒的位移和接触构成整个系统的计算单元。模型中主要包括球单元(ball)和墙单元(wall)，以及颗粒与颗粒接触和颗粒与墙接触。在PFC2D中，做了如下假设[9-12]：

(1)颗粒被视为刚体，不可变形。

(2)颗粒之间的接触是点接触，范围小。

(3)颗粒接触为柔性接触，允许一定的重叠，但重叠量相对于单元尺寸足够小。

(4)颗粒间可以存在粘结，且遵循力-位移定律。

软件采用显式中心差分法迭代计算颗粒的速度和加速度。每个计算步长内颗粒只与接触的颗粒相互作用，所有的颗粒遵循牛顿第二定律，墙不遵循牛顿第二定律。每次计算后更新球的位置，通过运动定律和力-位移定律反复迭代计算，且2种定律的计算同时进行。计算过程见图1。

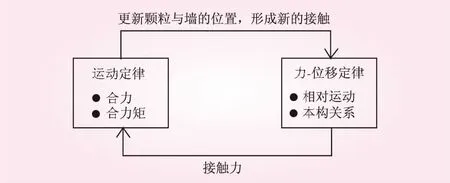
图1 PFC2D循环计算

1.2 运动方程

力-位移方程描述了颗粒间的力和位移关系，颗粒间法向力-位移方程为

ΔFn=knun

式中，Fn为法向接触力；kn为法向接触刚度；un为相对位移。

颗粒间切向力-位移方程为

ΔFs=ksus

式中，Fs为切向接触力；ks为切向接触刚度；us为相对位移。

颗粒的平动和转动是通过力和力矩计算平动加速度和转动加速度，再根据加速度计算颗粒在时间Δt内的平动位移量和转动位移量，以x方向为例，时间t0颗粒的平动加速度和转动加速度分布为

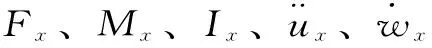
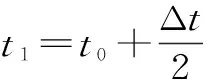
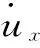
在时间t2=t0+Δt时，颗粒的位移为

式中，ux为x方向的位移。

1.3 连接模型

PFC2D颗粒连接模型包括接触点连接模型和接触平行连接模型。点连接模型只能传递力，用法向/切向连接强度定义，但不能传递力矩。当法/切向力大于法/切向连接强度时，连接破坏。而平行连接模型可以视为以接触点为中心的一系列均匀分布且相互平行的弹簧，可以传递力矩，用平行连接法向/切向强度定义。当法/切向应力大于法/切向连接强度时，连接破坏。对于库岸边坡覆盖层堆积物，选择平行连接模型更加吻合。

1.4 参数标定

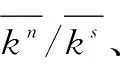
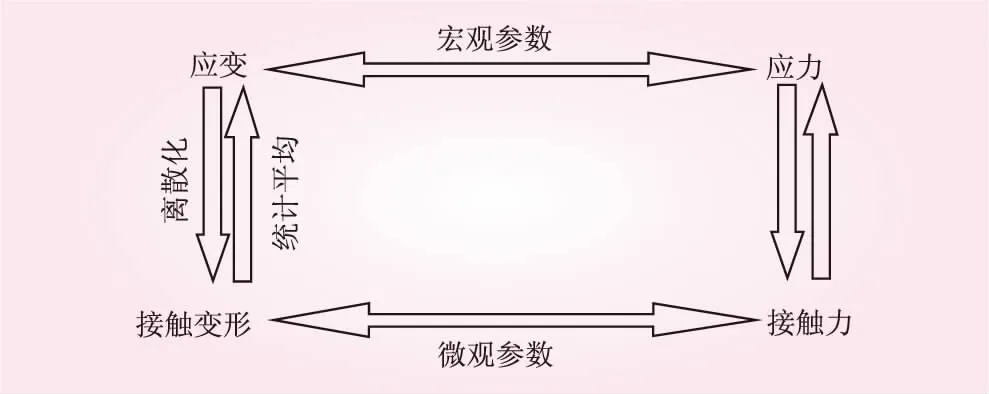
图2 宏观参数与微观参数关系

法向接触刚度kn/N·m-1切向接触刚度ks/N·m-1摩擦系数f非饱和状态平行法向连接强度/Pa·m-1平行切向连接强度/Pa·m-1密度/kg·m-3饱和状态平行法向连接强度/Pa·m-1平行切向连接强度/Pa·m-1密度/kg·m-36×1086×1080.69×1059×10519606.5×1056.5×1052100

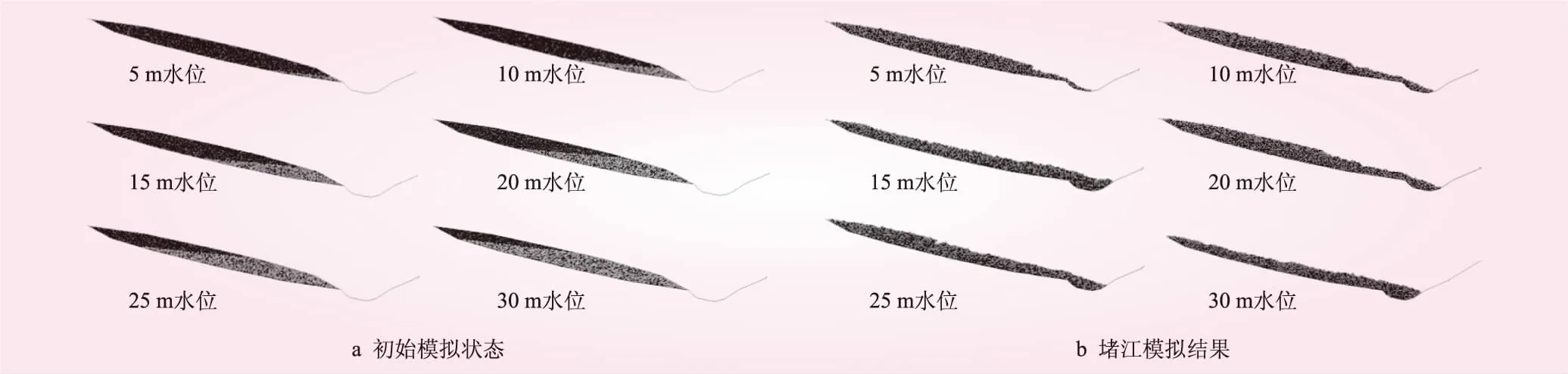
图5 各水位模拟结果

2 模型建立及结果分析

2.1 模型建立

由于水库的运行，在库岸边坡内会产生不同高度的地下水位，对覆盖层稳定性有较大的影响。建立的较理想的边坡模型见图3。覆盖层水平长200 m，纵向高差50 m，基覆面倾角约30°，河谷宽40 m，深9 m。假设在天然水位下覆盖层处于基本稳定状态，水库在运行工况下分别产生了高于河谷5、10、15、20、25 m和30 m的不同高度的地下水位。覆盖层的体积约为2 000 m3，天然水位下的覆盖层PFC模型见图4。本次计算模型共2 196个颗粒，粒径0.25～0.75 m。模型选用平行连接结构，在对微观参数进行调整之后，使模型处于欠稳定的临界状态。微观参数取值见表1。在不同水位高度下，饱和土体的比例见表2。各水位模拟结果见图5。

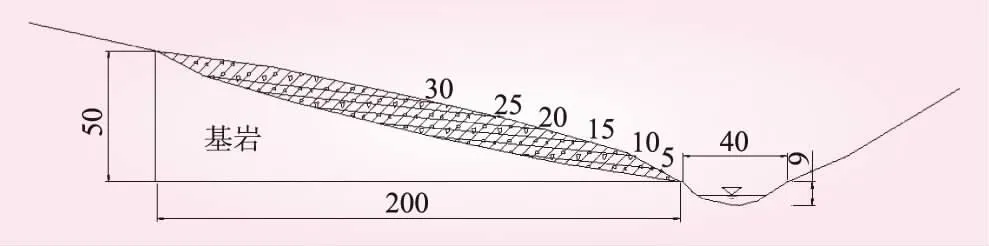
图3 理想的库岸边坡覆盖层(单位：m)

图4 天然水位下的覆盖层PFC模型

水位高度/m饱和土比例51∶20101∶5151∶3201∶2253∶5304∶5

2.2 结果分析

从图5可知，总体上，覆盖层破坏主要是由于底部土体在地下水的作用下力学参数降低，在河流侧蚀作用下发生局部破坏，进一步导致覆盖层临空状态的改变，再接着引起新的临空面产生，后续的破坏将继续进行。在水位为5、10 m和20 m时，覆盖层的破坏模式是塌岸，造成临空状态改变，但中～后段的土体并没有因此而产生较大的破坏。从趋势上看，水位越高，底部土体塌岸的规模越大，中～后段的变形量越大。在水位为25 m时，前～中段的土体发生了失稳，虽然后段的土体没有大量的位移，但也产生了新的较大的拉裂。在水位30 m时，覆盖层绝大部分被地下水浸没，整个覆盖层内部的力学强度降低，造成整体破坏。

斜坡失稳后造成的堵江高度见图6。从图6可知，在水位高度为15 m时，模拟的堵江高度是本次研究当中最大的，其破坏过程见图7。图中，T为运算步数。从图7可知，在初始时期，覆盖层的破坏主要是地下水位以下部分；中期阶段，饱和土体的下滑对上部非饱和土体产生一个拖拽力，主要发生在地下水位线附近，带动非饱和土体一起下滑，由于不断产生新的临空面，后面的土体不能达到平衡状态，因此也跟着下滑，最终导致斜坡的整体失稳。

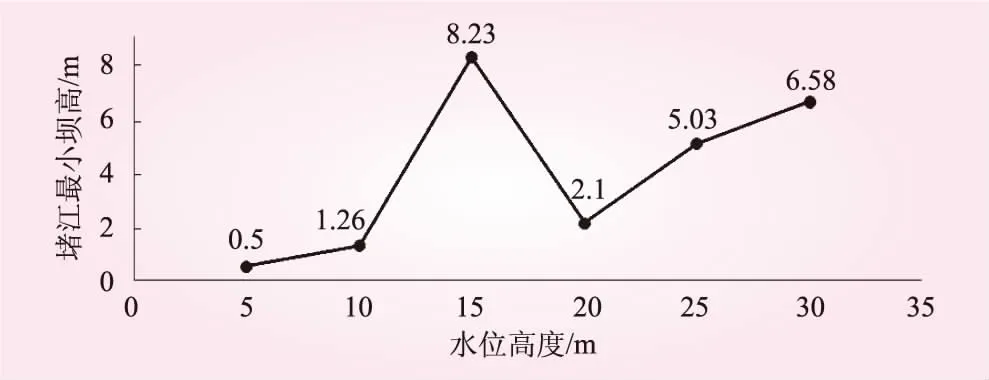
图6 地下水位高度与堵江坝高关系

图7 水位为15 m时斜坡破坏过程

用同样的方法分析其他地下水位高度时的破坏过程。在5 m和10 m时，由于坡脚的饱和土体下滑，产生新的临空面，但中～后段大部分土体未受到影响，其基本结构并未遭到改变，新形态的斜坡尚能达到平衡状态。在20 m和25 m时，斜坡失稳的主要部位是饱和土体，在饱和土体下滑后，非饱和土体位移并不明显，且在饱和土体下滑部位延伸至地下水位线时，并未造成饱和土体和非饱和土体一起大量下滑(同15 m时的情况)。其原因为上部非饱和土体并没有15 m时多，饱和土体能够支撑住非饱和土体，不使其进一步下滑。而30 m时，由于饱和土体下滑较多，造成了后段斜坡的不稳定。通过对比各地下水位高度时，斜坡覆盖层破坏后的堵江高度可知，整体上，地下水位越高，堵江堰塞坝高度越高，但在饱和土体的比例占1/3时，坝高比其相邻水位高出很多，即存在一个最危险水位。

3 结 语

本文基于PFC2D颗粒流程序，建立有覆盖层的库岸边坡模型，得出以下结论：

(1)整体上，地下水位越高，斜坡覆盖层失稳后堆积形成的堰塞坝高度越高。但在饱和土体的比例占1/3时，坝高比其相邻水位高出很多，即存在一个最危险水位。

(2)水位低于危险水位时，斜坡覆盖层主要破坏模式是坡脚塌岸；水位高于危险水位区域时，主要是饱和土体发生失稳，非饱和土体部分失稳并堆积在水位线附近。

虽然PFC2D能够较好地模拟土质斜坡堵江，但土体的微观参数取值较复杂，在有试验数据的条件下，可用双轴试验来标定参数；在没有试验数据时，则需类比和多次试模拟以确定微观参数。此外，静态水位可用PFC2D模拟，只能用于水库调动之后的水位稳定的情况，而对库水位升降造成的地下水渗流模拟难度较大。

参考文献：

[1] 孙蔚, 董云. 堵江滑坡坝的溃坝方式模拟与环境效应分析[J].自然灾害学报, 2008, 17(4)： 72- 77．

[2] 马建全. 黑方台灌区台缘黄土滑坡稳定性研究[D]. 长春： 吉林大学, 2012．

[3] 原俊红. 白龙江中游滑坡堵江问题研究[D]. 兰州： 兰州大学, 2007．

[4] 罗刚. 唐家山高速短程滑坡堵江及溃坝机制研究[D]. 成都： 西南交通大学, 2012．

[5] 徐文杰, 陈祖煜, 何秉顺, 等. 肖家桥滑坡堵江机制及灾害链效应研究[J]. 岩石力学与工程学报, 2010, 29(5)： 933- 942．

[6] 宋朋燃. 黄土边坡冲刷破坏特征及数值模拟[D]. 长春： 吉林大学, 2013．

[7] 周健, 王家全, 曾远, 等. 土坡稳定分析的颗粒流模拟[J]. 岩土力学, 2009, 30(1)： 86- 90．

[8] 梁承洋. 川藏交通廊道冰碛物滑坡堵江风险及线路对策研究[D]. 成都： 西南交通大学, 2015．

[9] 周健, 池永, 池毓蔚, 等. 颗粒流方法及PFC2D程序[J]. 岩土力学, 2000, 21(3)： 1- 4．

[10] CUNDALL P A, STRACK O D L. A discrete numerical mode for granular assemblies[J]. Géotechnique, 1979, 29(1): 47- 65．

[11] 彭博, 陈玉明, 袁利伟. 基于 PFC2 D马鞍山铁矿2号露天采场边坡稳定性分析[J]. 黄金, 2014(12)： 37- 40．

[12] 陈俊, 张东, 黄晓明. 离散元颗粒流软件(PFC)在道路工程中的应用[M]. 北京： 人民交通出版社股份有限公司, 2015．