基于频率组合的区间流域设计洪水计算方法
刘章君,成静清,温天福,吴向东,贾 磊
(1.江西省水利科学研究院,江西南昌330029;2.水利部鄱阳湖水资源水生态环境研究中心,江西南昌330029;3.江西省鄱阳湖水资源与环境重点实验室,江西南昌330029)
0 引 言
设计洪水的地区组成是大中型水利水电工程洪水计算的主要研究内容之一,它是确定流域梯级开发和工程设计规模的重要依据[1]。拟定设计洪水的地区组成时,需要区间各种防洪标准的设计洪量或洪量频率曲线,并且区间洪水成果对下游断面防洪影响较大[2-3]。因此,准确的区间设计洪水估算具有重要意义。
区间流域通常都缺少直接实测的洪水资料,因此只能采用间接资料或用间接方法计算。但在区间无暴雨资料或暴雨资料不足时,间接资料计算方法的应用受到限制。间接方法根据资料条件的不同主要分为[4]:①当上下游断面均有实测洪水资料时,可将历年下游断面洪水过程减去上游段面洪水过程(包括洪水演进),得到历年区间的洪水过程线。之后,按照传统的规范方法进行区间洪水频率计算。但这种方法在区间洪水所占比重较小时,二者相减的误差将严重影响区间设计洪水成果的精度。②当区间某一部分流域面积(如支流)上有水文站时,可参照水文站控制流域面积与区间总面积以及暴雨、产汇流特性等,将水文站的历年洪水过程转换成整个区间的洪水过程,再进行区间洪水频率计算。但当区间有水文站控制的流域面积较小时,使上述转换产生较大误差。方法①和②一般均只利用实测资料序列进行分析计算,难以考虑历史洪水资料,应用于资料系列较短的站点时,其估计结果难以满足工程实际要求。③采用区间所在的暴雨等值线图及暴雨径流查算图表进行计算,或者由相似流域经地区综合的经验公式来推求区间的设计洪水。这种方法一般精度较低,适用于无法采用上述方法①和②计算区间设计洪水的情形。
工程实际中以区间流域缺乏实测资料,而区间的控制边界上下游断面均有洪水资料及设计洪水成果的情况最为常见。由于区间洪量是下游断面洪量与上游洪量之差,不仅受上、下游洪量的影响,而且上、下游洪量有一定关系。因此,区间洪量的频率计算实质上可以看作为上、下游洪量的频率组合计算。本文从多变量函数的频率分析与计算角度,提出一种计算区间流域设计洪水的新方法;并以清江流域为例,推求水布垭坝址与隔河岩坝址之间的区间流域的洪量频率曲线,对该方法进行了验证。
1 区间流域设计洪水计算的频率组合模型
如图1所示,A为下游断面;B为上游断面,C为断面A与断面B之间的区间流域。X、Y及Z分别表示断面A、断面B和区间C的天然来水量。
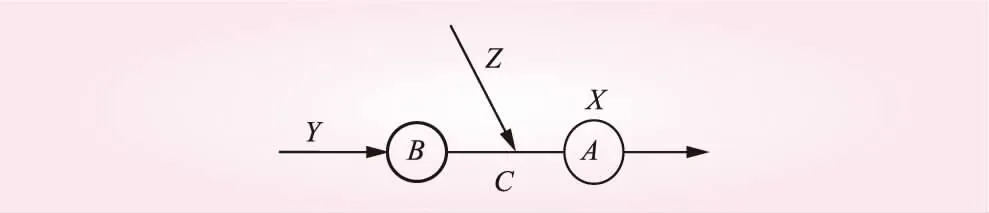
图1 区间流域示意
由水量平衡原理得
Z=X-Y
(1)
现欲推求Z的概率分布FZ(z)。Z不仅受X、Y的影响,且X和Y一般不是独立的,而是具有一定关系的。Z的频率计算实质上可以看成是X、Y的频率组合计算。
根据定义有
FZ(z)=P(Z≤z)=P(X-Y≤z)
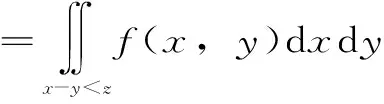
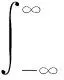

(2)
式中,f(x,y)为二元随机变量(X,Y)的联合概率密度函数。
对式(2)求导,可得

(3)
若已知联合概率密度函数f(x,y),在此基础上再积分计算,就可得到Z的概率分布。我国一般假定X和Y均服从P-III型分布[1],且它们之间还存在一定的相关性。若用传统办法来确定f(x,y)的解析表达式是非常困难的,因此直接应用式(3)积分求解Z的概率分布尚存在一定的困难,实际应用中只能采用一些近似的计算方法。
2 多变量函数频率分析与计算方法
对于多变量函数的频率分析与计算,常用的方法主要有统计参数法[6]和概率组合法[7]。随着联合分布模拟技术的不断发展,尤其是近年来Copula函数在水文领域的成功应用,学者们提出了基于Copula函数的蒙特卡罗法[8-10](以下简称“Copula-MC法”)和基于Copula函数的概率组合法[11](以下简称“Copula-PC法”)。本文将采用以上4种方法来计算Z的分布函数FZ(z),并对各方法进行比较分析。
2.1 Copula函数、联合分布和条件分布
(1)Copula函数及联合分布。Copula函数是定义域为[0,1]均匀分布的多维联合分布函数,根据Sklar定理,它可以将多个随机变量的边缘分布连接起来构造联合分布。选用在构造上下游断面洪水联合分布时应用最为广泛的Gumbel-Hougaard Copula函数作为下游断面A和上游断面B洪量的联合分布函数,数学表达式为[12]
F(x,y)=C(u,v)=exp{-[(-lnu)θ+
(-lnv)θ]1/θ}
(5)
式中,u=FX(x)和v=FY(y)分别代表边缘分布函数;θ为Copula函数的参数,采用可以考虑历史洪水信息的改进极大似然法估计。
(2)基于Copula函数的条件概率。当随机变量X、Y的联合分布F(x,y)确定后,给定X=x时,Y≤y的条件分布函数为
(6)
借助Copula函数,上式可表示为[13]
(7)
对于式(5)中Gumbel-Hougaard Copula函数,式(7)可具体表示为[14-15]
FY|X(y|x)=exp{-[(-lnu)θ+(-lnv)θ]1/θ}×
[(-lnu)θ+(-lnv)θ]1/θ-1(-lnu)θ-1/u
(8)
则依据概率分布的性质可知,当给定X=x时,Y≥y的条件概率
Py|x=P(Y≥y|X=x)=1-FY|X(y|x)
(9)
2.2 统计参数法
统计参数法就是根据式(1)计算Z的统计参数(均值、变差系数和偏态系数);再假定Z的频率曲线分布线型,即可得到Z的概率分布曲线。因此,该方法的关键是组合变量Z统计参数的计算。设随机变量X、Y均有n年的资料序列,则对应的Z也有n年的资料序列。
(1)均值
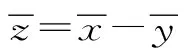
(10)

(2)变差系数。Z的方差为
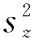
(11)
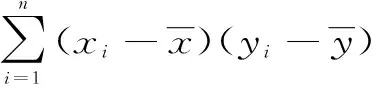
(12)
(3)偏态系数
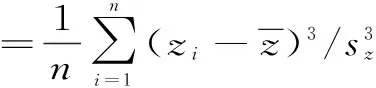
(13)
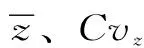
2.3 离散求和法
离散求和法是最常用的概率组合方法,将X与Y的频率曲线离散化,概化成有限个“状态”,即阶梯状,得到Z的所有组合状态,再推求所有组合状态的概率。该法一般假定X与Y相互独立。
设X、Y的每一状态对应一概率区间,即X取状态xi的概率区间为ΔPx,i(i=1,2,…,nx;nx为X的状态数),Y取状态yj的概率区间为ΔPy,j(j=1,2,…,ny;ny为Y的状态数),则Z的状态zij=xi-yj(zij的状态数nz=nx×ny),对应的概率区间为ΔPz,ij,则
P(Z=zij)=ΔPz,ij=P(X=xi)P(Y=yj)=ΔPx.iΔPy,j
(14)
于是有
(15)
当X与Y不独立时,一般应进行独立性处理,以新变量代换X或Y中的一个。在实际应用中,一般对均值较小的组合变量作变量代换,效果较好。不失一般性,假定Y的均值较小,可作如下变量变换
E=Y-k·X
(16)
根据正交性原理,当k为最小二乘估计时,即
(17)
则经独立性处理后,E与X满足正交条件,从而认为二者不相关;实际应用中一般可视为是相互独立的,可按独立随机变量一样进行频率组合计算。
2.4 Copula-PC法
当Y倚X的条件概率确定后,对于X的每一个取值状态,都对应一条Y倚X的条件概率曲线Py|x。将X的频率曲线离散化,即概化成阶梯状,离散后X只能取有限个状态值。对X的每一种取值状态,将其对应的Y倚X的条件概率曲线Py|x也离散化。设X取nx个状态,取ny个状态,则组合变量Z的状态nz=nx·ny。
X、Py|x的每一状态都对应一概率区间,设X取状态xi的概率区间为ΔPx,i,Y取状态yj的条件概率区间为ΔPyj|xi(i=1, 2, …,nx;j=1, 2, …,ny)。Z相应状态对应的概率区间为ΔPz,ij,则
P(Z=zij)=ΔPz,ij=P(X=xi)·P(Y=yj|X=xi)
=ΔPx,i·ΔPyj|xi
(18)
式中,zij=xi-yj;而
ΔPyj|xi=[1-FY|X(yj+1|xi)]-[1-FY|X(yj|xi)]
=FY|X(yj|xi)-FY|X(yj+1|xi)
(19)
于是式(19)可表示为
P(Z=zij)=ΔPz,ij=[FY|X(yj|xi)-
FY|X(yj+1|xi)]·ΔPx,i
(20)
则
(21)
可以看出,借助Copula函数可直接对Y倚X的条件概率曲线Py|x进行离散化,不需要对变量Y作独立性处理,保持了变量间的相关性特征,避免了离散求和法在进行独立性处理时可能出现的数据失真问题。
2.5 Copula-MC法
通过联合分布函数可以对存在相关性的随机变量X和Y成对地进行随机抽样,从而达到对二者同时随机模拟的目的。
步骤1:根据建立的两变量联合分布,可以得到当X为指定值时Y的条件分布,数学表达式为
SX(y|X=x)=P(Y≤y|X=x)=∂F(x,y)/∂x
(22)
步骤2:产生服从[0,1]均匀分布的两个独立随机数r1和r2。
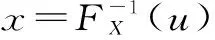
步骤4:令r2等于X=x时Y的条件分布值,即r2=SX(y|X=x),为求解方便,将式(7)表达为
SU(v|U=u)=P(V≤v|U=u)=∂C(u,v)/∂u
(23)

步骤5:通过z=x-y计算得到z。
步骤6:重复步骤2~5共n次,可以模拟出n个z值,再由期望公式计算经验频率,得到Z的频率曲线。P(z>zi)=mi/(n+1),mi为满足z 清江是湖北省境内最大的一条长江支流,发源于湖北省利川市齐岳山,流域面积1.7万km2,中下游建有水布垭-隔河岩梯级水库。如图1,A为隔河岩坝址断面,B为水布垭坝址断面,C为水布垭、隔河岩之间的区间流域(简称水-隔区间)。隔河岩坝址控制面积14 430 km2,其洪量由上游水布垭坝址(10 860 km2)和水-隔区间(3 570 km2)两个分区组合形成。水-隔区间左岸有泗渡河,右岸有泗扬河、天池河等较大支流,尽管泗渡河上设有招徕河水文站(1960年~1983年),集水面积792 km2,但只占水-隔区间面积的22%,资料系列也较短,因此间接方法②不宜采用。考虑到水布垭水电站坝址和隔河岩水电站坝址均有1965年~2010年的实测流量资料,且水-隔区间面积占隔河岩坝址控制面积的比例较大(24.7%),可采用间接方法①计算。本文将采用4种基于频率组合的方法计算水-隔区间最大3 d洪量的频率曲线,与采用传统间接方法①结果进行比较。 本文基本资料为1965年~2010年(共46 a)3 h时段的水布垭水电站坝址和隔河岩水电站坝址流量。计算最大3 d洪量频率曲线时隔河岩坝址1935作为特大洪水,水布垭坝址1883年和1997年作特大值处理。根据《水利水电工程设计洪水计算规范》,假设水布垭坝址和隔河岩坝址最大3 d洪量均服从P-Ⅲ分布,参数采用线性矩法初估,经适线法微调得到,估计结果见表1。 表1 清江流域水布垭和隔河岩坝址最大3 d洪量统计参数 分别采用1965年~2010年水布垭坝址和隔河岩坝址最大3 d洪量资料,利用可考虑历史洪水信息(实际上本实例无同步的历史洪水,但如果有的话可以考虑)的改进极大似然法计算得到联合分布的参数为6.05。将46 a的经验联合分布值与理论联合分布值点绘见图2,其确定性系数为0.993 3,经验频率与理论频率值的拟合情况很好。图3是另外一种形式对联合观测变量的经验联合分布值与理论联合分布值进行了对比。图2和图3表明所建立的联合分布是合理可行的。有了联合分布参数,分别代入式(5)和式(9)就可以得到联合分布函数和条件分布函数。 图2 联合观测值的经验分布和理论分布相关关系 图3 联合观测值的经验分布和理论分布比较 分别采用统计参数法、离散求和法、Copula-PC法和Copula-MC法,分别推求水-隔区间最大3 d洪量的频率曲线及设计值。 图4 5种方法计算的水-隔区间最大3 d洪量频率分布曲线 zij=0.278xi-ej (24) 该zij流量发生的概率为 图5 水-隔区间E的频率曲线 (25) 对X和E的全部取值状态作组合计算,可得Z的频率曲线(见图4)。 (3)Copula-PC法。以X的设计频率为0.1%和1%为例,即当X=x0.1%和X=x1%时,Y≥y的条件概率曲线分别见图6。将X的频率曲线和Y倚X的条件概率曲线都离散成40种状态,设变量X第i种状态的取值为xi,Y取状态yj的条件概率区间为ΔPyj|xi,则 zij=xi-yj (26) 图6 给定X=x0.1%和X=x1%时Y的条件频率曲线 该zij流量发生的概率为 ΔPz,ij=ΔPx,i·ΔPyj|xi=ΔPx,i·[FY|X(yj|xi)- FY|X(yj+1|xi)] (27) 对X和Y的全部取值状态作组合计算,可得Z的频率曲线(见图7)。 图7 水布垭与隔河岩最大3 d洪量随机生成散点 (4)Copula-MC法。运用上述2.5节中的Copula-MC法计算步骤,模拟15 000组水布垭坝址和隔河岩坝址最大3 d洪量。将模拟结果和46 a实测资料结果点绘于图7。由图7可知,实测资料点据都位于随机模拟散点图中,对实测资料的吻合效果较好。Copula-MC法不但实现了水-隔区间最大3d洪量的随机生成,同时增加了隔河岩坝址洪水地区组成随机性和多样性。利用上述随机生成的大量水-隔区间最大3 d洪量,采用期望公式计算的经验频率,得到Z的频率曲线。 《隔河岩水库汛限水位设计与运用技术报告》[16]中采用传统的间接方法①计算水-隔区间最大3 d洪量的频率曲线。将以上4种频率组合方法和文献[16]中的结果分别绘于图4,同时将5种常用设计频率的结果汇总于表2。 从图4和表2的计算结果可以发现:与两种基于Copula函数的Copula-PC法和Copula-MC法相比,传统的统计参数法和离散求和法计算的结果明显系统偏小,且偏小幅度随着洪水重现期的增大而增大,会低估设计断面的防洪风险。统计参数法只考虑上、下游断面的线性相关关系,而未真实反映两者复杂的非线性相关结构;同时假定Z服从P-Ⅲ分布理论上也缺乏依据。离散求和法在独立性转换的过程中,区间E系列出现大量负值并人为假定E服从P-Ⅲ分布进行强制适线,以致出现数据失真,造成误差较大。 表2 水-隔区间最大3 d洪量设计值对比 Copula-PC法采用Copula函数求解条件概率曲线,直接对其进行离散组合,不需要变量进行独立性处理,保持了变量间的相关性特征。Copula-MC法则通过Copula函数构建X和Y的联合分布函数,采用蒙特卡罗方法对其进行联合抽样,随机生成大量的水-隔区间最大3d洪量,从而得到频率曲线,计算结果合理,可操作性强。 本文提出的方法用清江流域水布垭-隔河岩区间流域实例进行验证的结果表明: (1)所提出的基于上下游断面洪水频率组合计算区间流域设计洪水的思路合理可行,推荐采用基于Copula函数的Copula-PC法和Copula-MC法。 (2)统计参数法和离散求和法理论上存在不足,计算的结果系统偏小,可能会低估下游断面的防洪风险。 (3)本文方法对资料条件要求较低,一般容易满足,且在频率组合过程中可以考虑历史洪水信息,更加符合工程实际要求。 参考文献: [1] 郭生练, 刘章君, 熊立华. 设计洪水计算方法研究进展与评价[J]. 水利学报, 2016, 47(3): 302-314. [2] 周祥林, 燕文明. 混联型梯级水库群的典型洪水地区组成[J]. 水力发电, 2016, 42(11):91-94. [3] 谭乔凤, 雷晓辉, 王浩, 等. 考虑梯级水库库容补偿和设计洪水不确定性的汛限水位动态控制域研究[J]. 四川大学学报: 工程科学版, 2017, 49(1): 60- 69. [4] 水利部长江水利委员会水文局, 水利部南京水文水资源研究所. 水利水电工程设计洪水计算手册[M]. 北京: 中国水利水电出版社, 2001. [5] SL 44—2006 水利水电工程设计洪水计算规范[S]. [6] 金光炎. 一个计算组合频率的新方法[J]. 中国水利, 1958(4): 46- 52. [7] 王锐琛, 陈源泽, 孙汉贤. 梯级水库下游洪水概率分布的计算方法[J]. 水文, 1990(1): 1- 8. [8] 肖义, 郭生练, 熊立华, 等. 一种新的洪水过程随机模拟方法研究[J]. 四川大学学报: 工程科学版, 2007, 39(2): 55- 60. [9] 张超, 胡志根, 刘全. 上游水电站控泄条件下施工导流风险分析[J]. 水利学报, 2012, 43(11): 1328- 1333. [10] 刘章君, 郭生练, 胡瑶, 等. 基于Copula-Monte Carlo法的水库下游洪水概率分布研究[J]. 水力发电, 2015, 41(8): 17- 22. [11] 李天元, 郭生练, 刘章君, 等. 梯级水库下游设计洪水计算方法研究[J]. 水利学报, 2014, 45(6): 641- 648. [12] 郭生练, 闫宝伟, 肖义, 等. Copula 函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008, 28(3): 1- 7. [13] 史黎翔, 宋松柏. 基于Copula函数的两变量洪水重现期与设计值计算研究[J]. 水力发电学报, 2015, 34(10): 27- 34. [14] 冯平, 李新. 基于Copula函数的非一致性洪水峰量联合分析[J]. 水利学报, 2013, 44(10): 1137- 1147. [15] 刘和昌, 梁忠民, 姚轶, 等. 基于Copula函数的水文变量条件组合分析[J]. 水力发电, 2014, 40(5): 13- 16. [16] 武汉大学水资源与水电工程科学国家重点实验, 长江勘测规划设计研究院, 长江水利委员会水文局. 隔河岩水库汛限水位设计与运用[R]. 武汉: 武汉大学, 2010.3 实例研究
3.1 研究区域概况
3.2 边缘分布、联合分布和条件分布

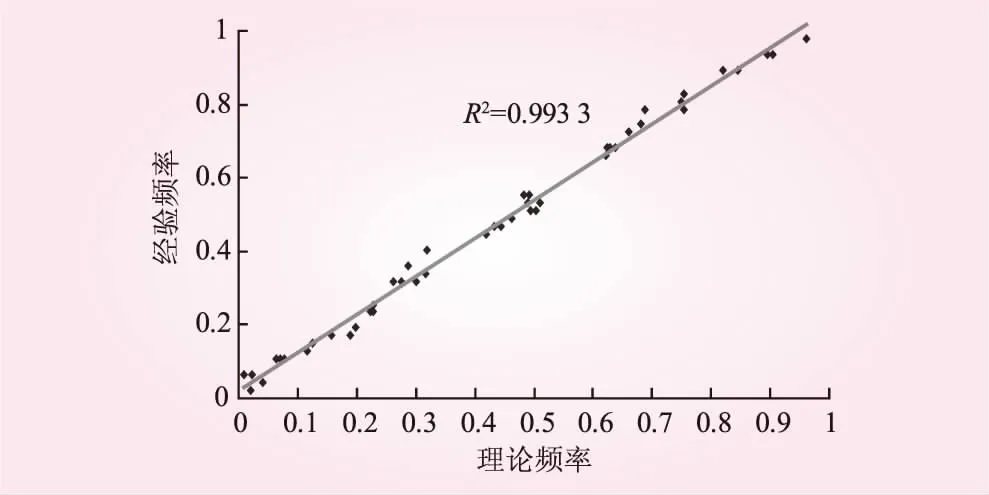

3.3 水-隔区间最大3 d洪量频率曲线
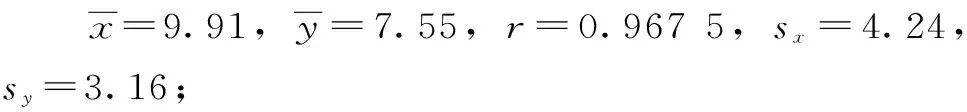
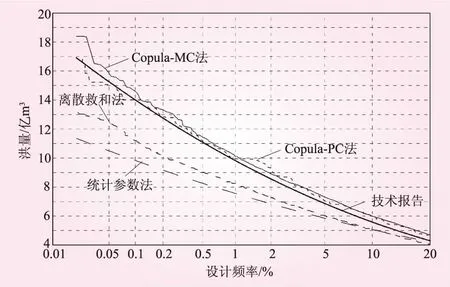

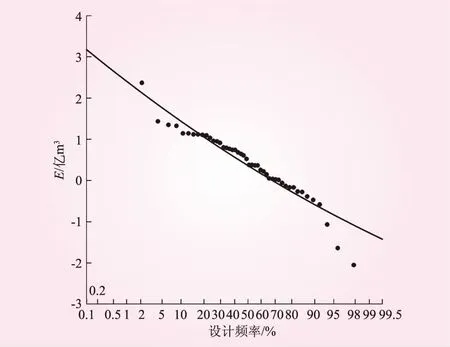
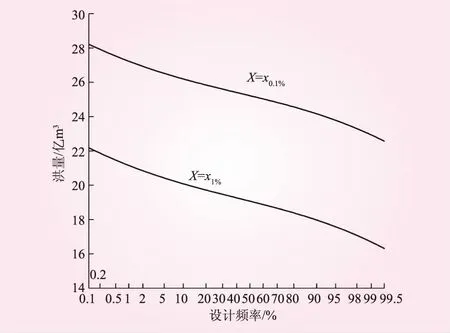

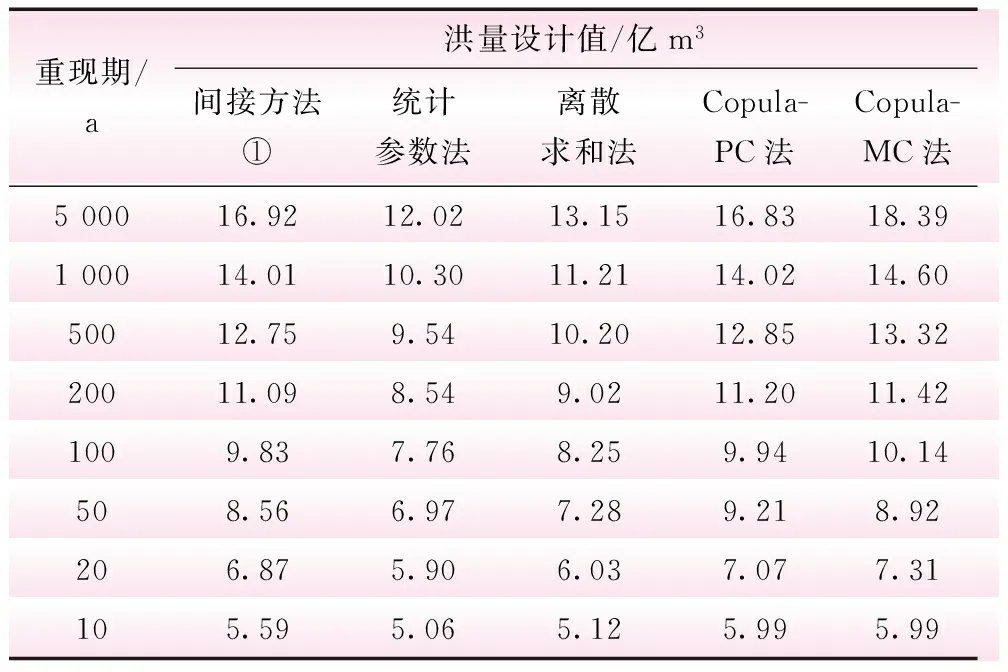
4 结 论

