非恒值磁链幅值给定SVM-DTC系统改进磁链观测器

郭梓浩，刘凤春

(大连理工大学，大连 116024)

0 引 言

直接转矩控制(以下简称DTC)是20世纪80年代中期针对异步电动机提出的，该方法不仅避免了矢量控制的复杂坐标变换，且控制对电动机参数的依赖性小，是一种性能优越的电动机控制方法。鉴于DTC的优点，1996年由新南威尔士大学和中国南京航天航空大学率先将直接转矩技术应用到正弦波永磁同步电动机的控制系统中。基于永磁同步电动机自身所具有的优点，永磁同步电动机的DTC策略得到了飞速的发展。后续的研究有将空间电压矢量调制应用到直接转矩系统(SVM-DTC)，以期减小输出转矩的脉动，并取得了良好的成果。

在DTC系统中，定子磁链观测器的性能影响着控制系统的性能。只使用纯积分器的磁链观测器，容易出现积分饱和现象。磁链观测出现积分饱和则会影响到控制对象的输出稳定性，且在运行中若不能及时有效地消除积分饱和，容易造成控制对象的输入量过高，导致系统崩溃不能运行。将高通滤波器串联在纯积分器后构成的低通滤波器，在定子磁链观测中解决积分饱和问题有着良好的表现。

文献[1]提出利用PI闭环校正的一阶低通滤波磁链观测器，考虑到定子电动势在出现直流偏置时，会破坏其与定子磁链的正交关系。利用PI校正环节对正交关系进行校正。文献[2]提出3种用于异步电动机磁链观测的定子磁链改进观测器，采用反馈的方式对一阶低通滤波观测器进行补偿。文献[3]控制系统采用了多阶层叠式可编程低通滤波算法代替普通的低通滤波算法，其有效解决了普通低通滤波算法估算时的稳态误差，但多阶层叠式可编程低通滤波算法实现复杂且动态性能差，限制了其应用。文献[4]提出一种包含五阶低通滤波器和一个高通滤波器的磁链估算结构，但该方法运算量大，且不容易实现。本文采用文献[1]提出的第二种改进型积分器进行研究，对其进行幅值限定的改进，使其适应于非恒值磁链幅值给定的SVM-DTC系统。

1 非恒值磁链幅值给定原理

非恒值磁链幅值给定的原理与最大转矩电流比的原理基本相似。文献[6]指出永磁同步电动机不必要将定子磁链幅值|ψs|控制为定值，考虑到电动机功率因数以及定子电流的大小，SVM-DTC系统可以借鉴矢量控制取isd=0的控制方法，将隐极式永磁同步电动机控制成isd=0。但永磁同步电动机的DTC系统中没有电流环的，对电流不能直接控制，需要借助对定子磁链幅值|ψs|的控制来达到isd=0的控制要求。

永磁同步电动机的定子磁场分别由永磁体产生的励磁磁场ψf以及定子电流产生的电枢磁场合成，本文针对表贴式永磁同步电动机isd=0控制要求给出的磁链矢量图如图1所示。因为控制isd=0，则意味着不同时刻定子电流一直全部为q轴电流，定子电流产生的电枢磁场全部在q轴上，d轴上的励磁磁场矢量一直是转子磁链矢量ψf，则在不同时刻合成得到的ψs1，ψs2定子磁链矢量都不会受到直轴电流的影响。

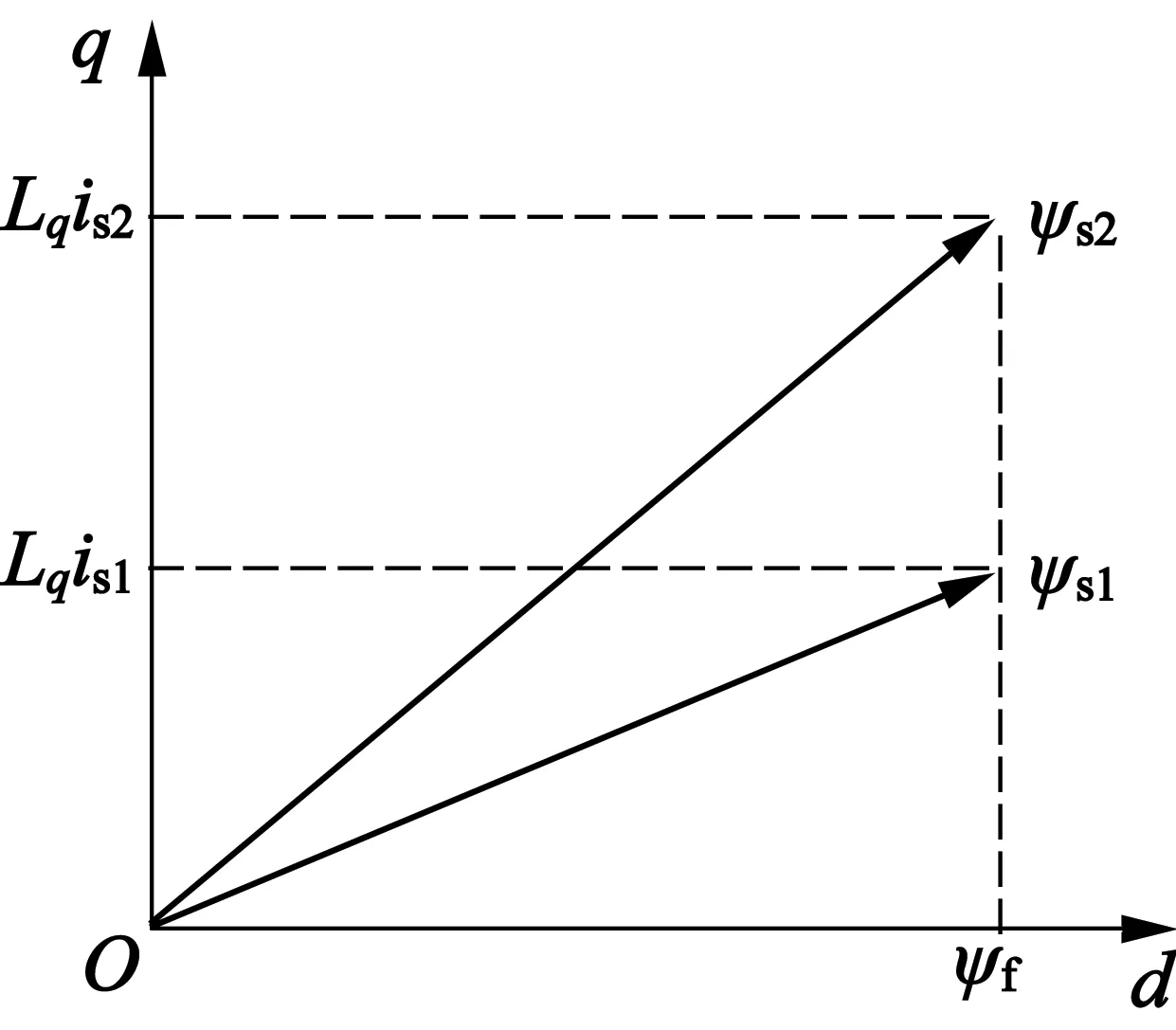
图1 isd=0磁链矢量图

隐极式永磁同步电动机的定子磁链和电流的关系：

(1)

电磁转矩表达式如下：

Te=1.5p(ψsdisq-ψsqisd)

(2)

式中：Te是电磁转矩；p是电动机的极对数。将isd=0的条件代入式(1)和式(2)，可以得到定子磁链幅值|ψs|的表达式如下式：

(3)

式(3)中，p，ψf，Lq是电动机的常数，是一个确定的值，所以影响磁链幅值给定值的因素只剩下电磁转矩Te，因此可以根据输出的电磁转矩的变化来控制磁链幅值的给定值。图2为非恒定磁链幅值给定SVM-DTC系统框图。图2与恒定磁链幅值给定SVM-DTC系统基本控制原理基本一致。系统通过采集电动机输入电流进行坐标变换后送入定子磁链观测器，以及转矩观测器得到估计的定子磁链以及转矩信息，将定子磁链观器测到的信息以及负载角增量信息送入到参考矢量的计算模块，进而得到参考矢量。将其送入到脉冲生成模块输出控制脉冲进行控制逆变器。

图2 非恒值磁链幅值给定SVM-DTC控制框图

对于图2非恒值磁链幅值给定SVM-DTC系统来说，其磁链幅值给定是通过实时根据转矩变化而变化，所以生成的参考矢量也会跟随变化。在同样对于图2非恒值磁链幅值给定SVM-DTC系统来说，其磁链幅值给定是通过实时根据转矩变化而变化，所以生成的参考矢量也会跟随变化。在同样的转矩给定下，因控制d轴电流为零，图2的系统相比于恒定磁链幅值给定SVM-DTC系统，前者能有效地减小电动机的输入电流。在转矩不超出最高转矩要求的情况下，提高在不同负载下的功率因数。

2 定子磁链观测

传统DTC的控制对象是电磁转矩以及定子磁链，从式(2)可以看出定子磁链的观测对于电磁转矩的计算有着至关重要的作用。因此，准确观测定子磁链是实现DTC的重要前提。当定子磁链观测不准确时，会导致永磁同步电动机失稳。

定子磁链电压模型如下：

(4)

(5)

(6)

式中：ψsα和ψsβ为定子磁链矢量在两相静止坐标系中的坐标分量；usα和usβ为定子电压坐标分量；isα和isβ为定子电流坐标分量；|ψs|为定子磁链幅值；θ为定子磁链的相位。

传统的定子磁链观测采用纯积分模型，该模型具有计算简单、参数依赖少等优点，但纯积分模型也有不可忽视的缺点，就是会产生积分饱和问题以及初值问题。通常的解决办法是采用低通滤波器代替纯积分器进行计算，但只采用低通滤波器则必然会产生幅值的衰减以及相位的误差。根据文献[2]提出的3类改进型积分器用于改善异步电动机定子磁链的观测。较为常用的是第二类的改进型积分器，该积分器对观测到的磁链相位不失真地反馈到输入端，只是对定子磁链的幅值进行饱和限幅，从而获得良好的观测效果。第二类改进型积分器的结构如图3所示。

该积分器的主要思想可以通过下式表述：

(7)

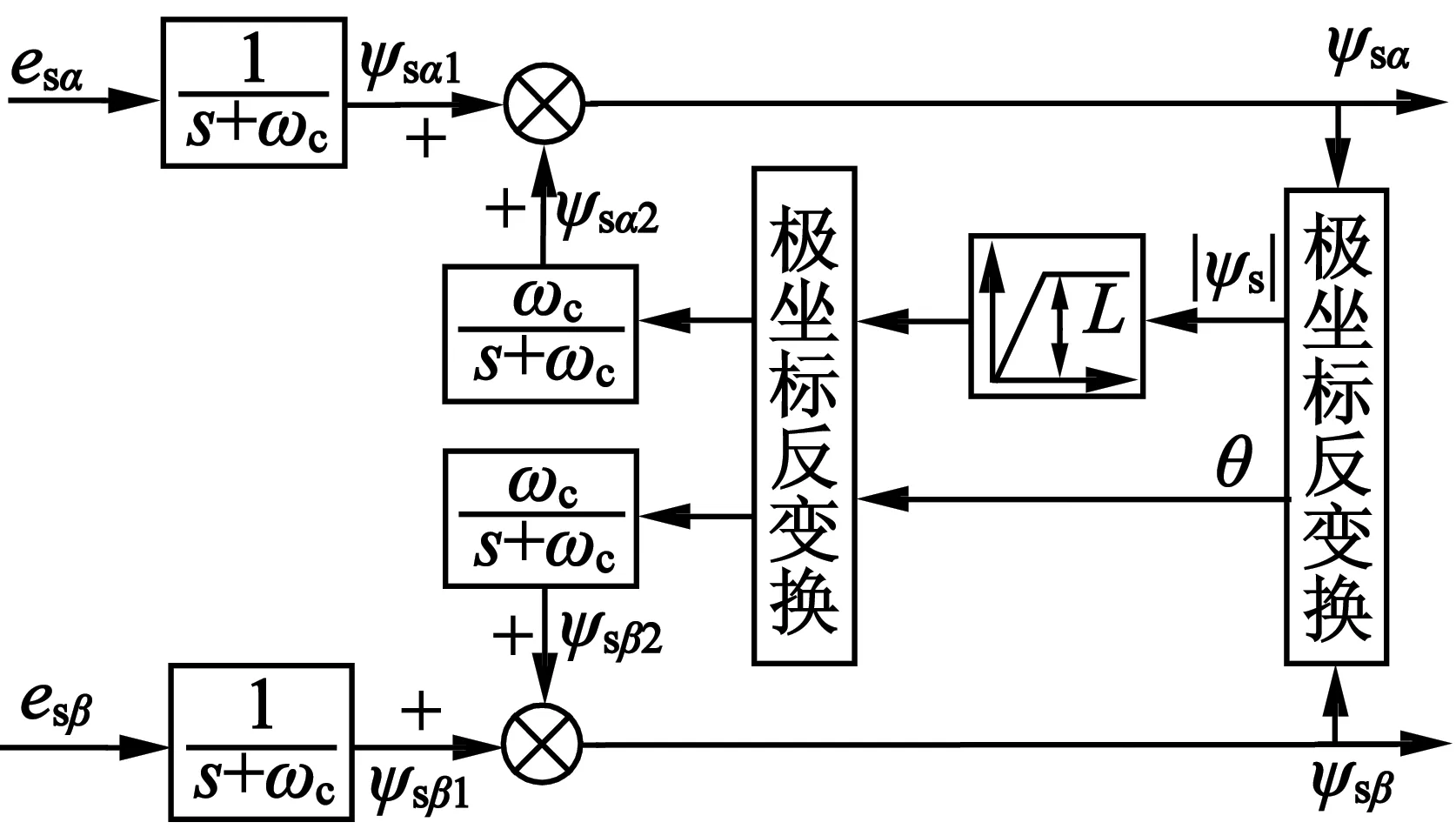
图3 第二类改进型积分器

式中：x，z为积分器输入信号和补偿信号；y为积分器的输出信号；ωc为低通滤波器的截止频率。

当z为0时，积分器为一阶滤波器，当z=y时，则积分器相当于纯积分器。

第二类改进型的积分器在电动机磁链幅值恒定的情况下有着良好的磁链估计效果，其准确性受饱和限幅的基准选取影响，而且在本文的非恒值磁链幅值给定的情况下，第二类改进型的积分器出现补偿不足以致于输出性能变坏。

2.1 变限幅积分器

第二类改进积分器是饱和幅值限定的积分器，其关键在于饱和幅值基准的选取。该积分器输入如果长期超出饱和幅值基准，则其输出性能会有所变坏。针对本文所研究的非恒值磁链幅值给定系统，第二类改进积分器不再适用。为了解决限幅值L的敏感性问题，本文提出一种简便有效的改进方法，即将幅值的限定改为动态幅值给定，其幅值给定跟随非恒值磁链幅值系统的给定，这样能有效解决第二类改进积分器在非恒定幅值给定系统里的补偿不足的问题。

图4为变限幅改进积分器的结构图。以ψsα为例，当积分器输出小于限幅值时，改进型积分器与纯积分器无异；当输入中混入直流偏移时通过低通滤波器后，输出的幅值衰减需要由反馈进行补偿。这时候对磁链的幅值需要进行饱和限幅，新型的改进型积分器将限幅值用变化的磁链幅值给定进行限幅，只要ψsα瞬时值的绝对值达到或者超出了限幅值时，积分器能有效地解决恒定限幅值所带来的幅值补偿不足的问题。

图4 新型变限幅改进型积分器

(8)

(9)

式中：A为输入信号幅值系数；B为输入信号的直流成分；C为和初始条件有关的系数；φ为经过低通滤波器的相位偏移，φ=arctan(ωc/ω)。

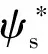
(10)

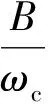
3 仿真分析及对比

根据上文的分析，利用MATLAB中Simulink仿真软件对图2进行搭建模型仿真。用图3和图4的积分器结构代替其磁链观测模块，分别观察其输出波形。

仿真用永磁同步电动机为表贴式正弦波永磁同步电动机，其相电阻R= 0.958 5 Ω；d-q轴电感Ld=Lq=0.00525H；永磁体建立永磁体磁链ψf= 0.1827Wb；转动惯量J=0.632 9×10-3kg·m2；极对数p=4；母线直流电压u=300 V。电动机给定转速为750 r/min，给定负载转矩为5 N·m。

图5是使用两种积分器后的电动机输出转矩的对比图。当采用第二类积分器进行观测磁链时，在电动机起动时有较大的转矩上升。可以知道，此时的q轴电流波形与转矩波形一致，转矩的上升会导致q轴电流的幅值过高，最终影响电动机的定子电流幅值。而对比与使用新型变限幅改进型积分器的电动机输出转矩可以看出，采用新型的变限幅值改进型积分器的电动机能有平稳的电动机起动转矩，且转矩值稳定在限幅值，有利于电动机的平稳安全起动。

(a) 采用第二类积分器

(b) 采用变限幅积分器

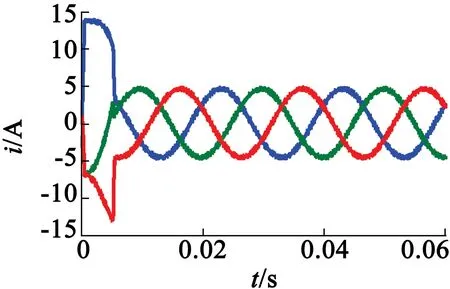
图6为电动机定子三相电流波形图。对定子磁链观测不准会引起电动机的定子电流畸变如图6(a)所示。实际运行中若出现这样的畸变电流，代表电动机的定子电流中含有不同阶次的谐波电流，对电动机的正常运行以及电子元器件的寿命都有不同程度的影响。

从图6(b)分析可以知道，使用变限幅积分器后，因为定子磁链观测准确，所以定子电流能达到正常的正弦电流波形，符合系统的正常运行要求，总的定子电流幅值有所减小，实际运行中能有效减少损耗的产生。

(a) 使用第二类积分器后

(b) 使用变限幅积分器后

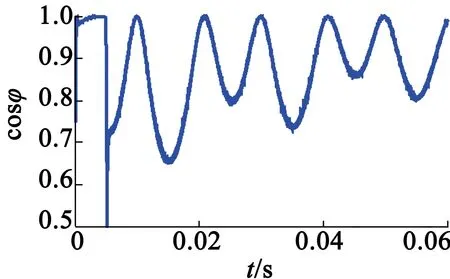
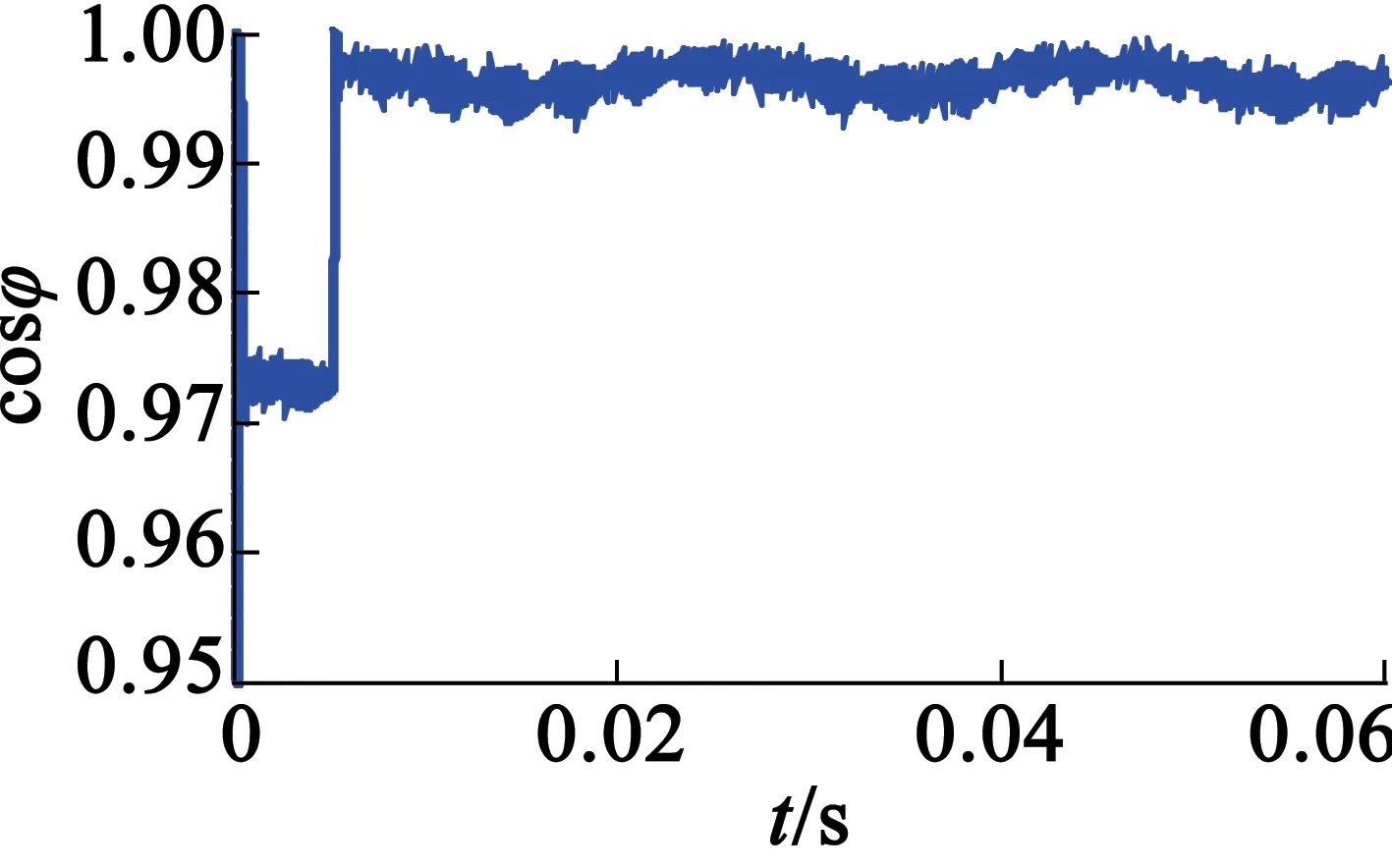
使用变限幅积分器后，电动机的功率因数在稳定运行时能基本稳定在0.996附近，如图7所示，符合非恒值磁链幅值给定控制系统能保证电动机呈现高功率因数的特点。而使用第二类积分器进行磁链观测时，因为对其磁链观测不准，导致电动机输出的d轴电流不能保持为0，功率因数不能维持在定值，这与非恒值磁链幅值给定的初衷是相违背的。

(a) 使用第二类积分器后

(b) 使用变限幅积分器后

非恒值磁链幅值给定系统的磁链幅值给定模块是根据电动机的输出转矩实时改变的，所以在电动机起动时，需要用较高的输出转矩将转子带到给定的转速值。磁链幅值给定在起动时有较大的幅值，如图8中半径较大的圆弧所示。后面系统稳定运行根据负载转矩控制定子磁链的幅值动态变化，控制isd=0来获得高的系统功率因数。

图8 变限幅积分器定子磁链圆

图9中虚线为使用第二类积分器在非恒值磁链幅值给定系统中的α轴磁链输出波形，点横线是理想纯积分器输出波形，实线是变限幅积分器输出波形。

图9 两种积分器输出α轴磁链对比

图9中点横线波形与实线波形相重合，证明变限幅积分器在系统运行中的表现理想，能拥有纯积分器的理想性质，且又有低通滤波积分器结构的优点。反观第二类积分器的磁链输出，其相位有所偏移，且正弦度差，会有波头一大一小的现象出现。原因是第二类积分器的饱和限幅值会提前限定输出磁链的补偿值的最大值，导致补偿不足。所以第二类积分器输出的磁链波形正弦度差，对系统的定子电流及稳定运行等都有不同程度的影响。

4 结 语

本文针对永磁同步电动机SVM-DTC控制方法的优良性能，将磁链给定模块替换成非恒值磁链幅值给定的模块，改良以往传统恒定磁链幅值的低功率因数的缺点。针对传统第二类改进型恒限幅值积分器的局限性，提出一种新的变限幅值积分器，通过这种方法可以在非恒定磁链幅值给定的DTC系统中表现优秀，并对其分析了理论上的可能性。本文以表贴式永磁同步电动机为例，在MATLAB/Simulink仿真软件对两种积分器在非恒定磁链幅值给定系统里性能进行仿真，并对其输出转矩、定子电流及功率因数等性能指标进行分析，采用新的变限幅值积分器的非恒值磁链幅值给定的SVM-DTC系统可以实现isd=0的控制效果，且电动机运行稳定，功率因数提高。

[1] 李春杰,李旭春.一种改进的直接转矩控制系统定子磁链观测方法[J].电机与控制应用,2006,33(6):32-35.

[2] HU J,WU B.New integration algorithms for estimating motor flux over a wide speed range[J].IEEE Transactions on Power Electronics,1998,13(5):969-977.

[3] BOSE B K,PATEL N R.A programmable cascaded low-pass filter-based flux synthesis for a stator flux-oriented vector-controlled induction motor drive[J].IEEE Transactions on Industrial Electronics,1997,44(1):140-143.

[4] WANG Y,DENG Z.An integration algorithm for stator flux estimation of a direct-torque-controlled electrical excitation flux-switching generator[J].IEEE Transactions on Energy Conversion,2012,27(2):411-420.

[5] QIU X,HUANG W,BU F.An improved direct torque control method for PMSM[C]//Applied Power Electronics Conference and Exposition (APEC). IEEE,2014:2421-2424.

[6] 杨建飞,胡育文.永磁同步电机最优直接转矩控制[J].中国电机工程学报,2011,31(27):109-115.

[7] 刘刚,孙庆文,肖烨然.基于改进反电势积分的永磁同步电机位置检测[J].电机与控制学报2016,20(2):36-42

[8] 郎宝华,刘卫国,贺虎成,等.基于最大转矩电流比动态磁链给定的直接转矩控制[J].电气传动,2008,38(1):23-26.

[9] 刘红伟,范永坤,熊皑.一种新的直接转矩控制的定子磁链幅值给定机制[J].微电机,2014,47(1):66-70.

[10] 唐校,杨向宇,赵世伟,等. 非恒定磁链幅值给定的永磁同步电机直接转矩控制[J].电力自动化设备,2015(9):37-42.

[11] 许峻峰,徐英雷,冯江华,等.基于改进型积分器的永磁同步电机直接转矩控制[J].电工技术学报,2004(7):77-80,94.

[12] 孙丹,贺益康.基于恒定开关频率空间矢量调制的永磁同步电机直接转矩控制[J].中国电机工程学报,2005(12):112-116.