基于二阶滑模算法的永磁同步电机控制
杨 婧,纪科辉,赵新龙,鲁文其
(浙江理工大学,杭州 310018)
0 引 言
永磁同步电机在运动控制领域中占据着主导地位,如何准确地测量电机的速度是精确控制的前提。电机控制中最经典的是比例积分微分调节(以下简称PID)控制,由于PID控制器结构简单、容易数字实现等优点,使用广泛。单纯的PID控制系统参数依赖性强,鲁棒性差,抗负载扰动能力很有限,降低了系统的控制性能,因此很难满足高精度伺服控制系统的要求[1]。
为了提高电机的控制性能,使得电机在实际控制中获得良好的动态响应,学者针对上述问题提出了一些鲁棒控制方法,如神经网络控制、非线性控制、模糊控制、自适应控制和滑模控制等[2]。
滑模控制因具有对永磁同步电机系统参数时变和对外部干扰的强鲁棒性,成为国内外学者研究的热点领域[3]。传统的一阶滑模控制存在一些不可忽视的缺点。由于控制过程中的不连续性,系统在运行过程中容易引起抖振,而抖振将严重影响伺服系统的准确度和稳定度[4-5]。研究表明,在准确设计和调节滑模参数的前提下,滑模观测器能够较为准确地估计系统的参数[6-7]。
本文针对如何提高电机系统的动态性能的问题,提出了一种电机速度的二阶滑模算法。算法不仅保留了滑模控制的优点,并且能够从根本上消除抖振现象。该算法通过对实际位置信号的检测,来计算实际速度值,从而实现对电机转速的反馈调节。
1 滑模算法的原理
考虑一个动态系统:
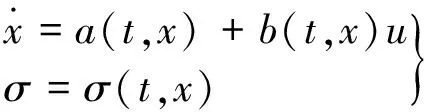
(1)
式中:x∈Rn为状态变量(Rn为n维实数空间);u∈R为控制函数的输入(R为实数集);a(t,x),b(t,x)为不确定的光滑函数;σ(t,x)为输出函数,σ和n是未知的。假设该系统的相对度为2,为使输出σ在有限时间消失,并且通过一种不连续的全局有界反馈控制来保持σ≡0,系统的轨迹应该在任何有限输入时间内被无限延伸[8]。
(2)
式中:函数h(t,x),g(t,x)为未知的光滑函数。由于控制函数u有界并且连续,假设输入输出条件如下:
(3)
式中:C,Km,KM∈R+(R+为正实数集)。
在设定的有限区间内,由式(2)和式(3)得到:
(4)
设定反馈函数:
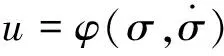
(5)
2 二阶滑模算法的设计
二阶滑模方法可以应用于永磁同步电机速度的计算[9-10],根据上节所述的二阶滑模算法提出了一种具有微分结构的二阶滑模速度计算方法。
二阶滑模的微分算法计算框图如图1所示。

图1 二阶滑模算法
积分器的输出信号θ1(t)和ω1(t),分别跟踪输入信号θ(t)和它的微分信号,驱动信号u(t)是数字控制的分段恒定输出。设a[k]=a(kT)表示一个通用信号a(t)在采样时刻t=kT的采样值,k=0,1,2,…,其中T为采样周期。
(6)

(7)
如果一个正常数X2是已知的:
(8)

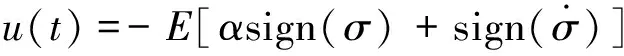
(9)
式中:E,α为滑模控制函数的增益。

根据式(6)和式(7),可得电机加速度u(t)和转速ω1(t)的计算框图,如图2所示。
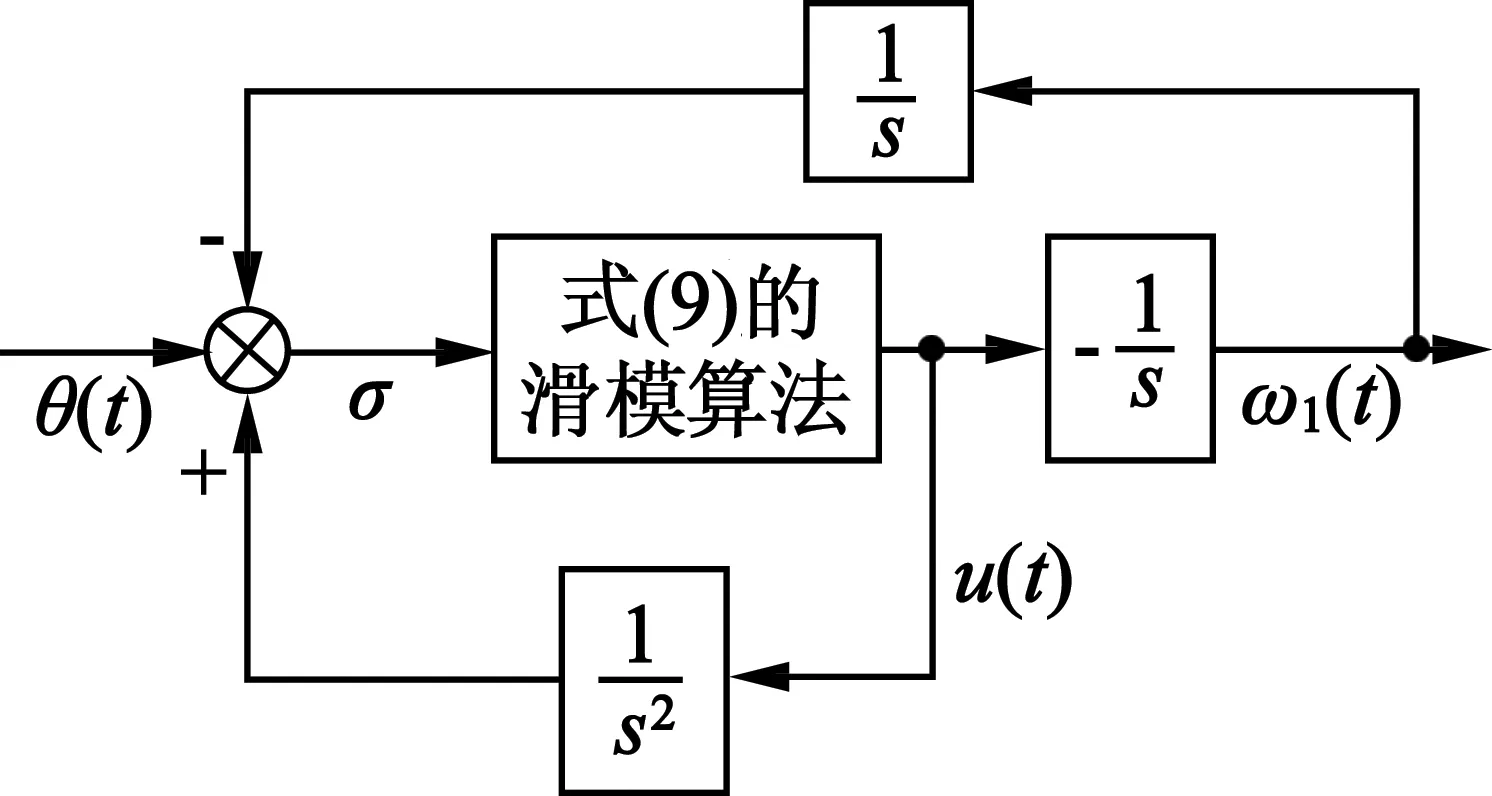
图2 电机加速度和速度的计算
3 仿真结果与分析
传统的永磁电机驱动器采用的是PI闭环控制,速度由位置信号直接微分得到。但是由于在电机的实际系统运行过程中,其负载经常受到外界扰动,负载扰动会影响系统的动态性能。为使伺服系统具有良好的鲁棒性和速度跟踪性能,必须克服负载扰动对电机转速的影响。
本文在传统PI闭环控制模型的基础上加上二阶滑模速度计算模块,如图3所示。
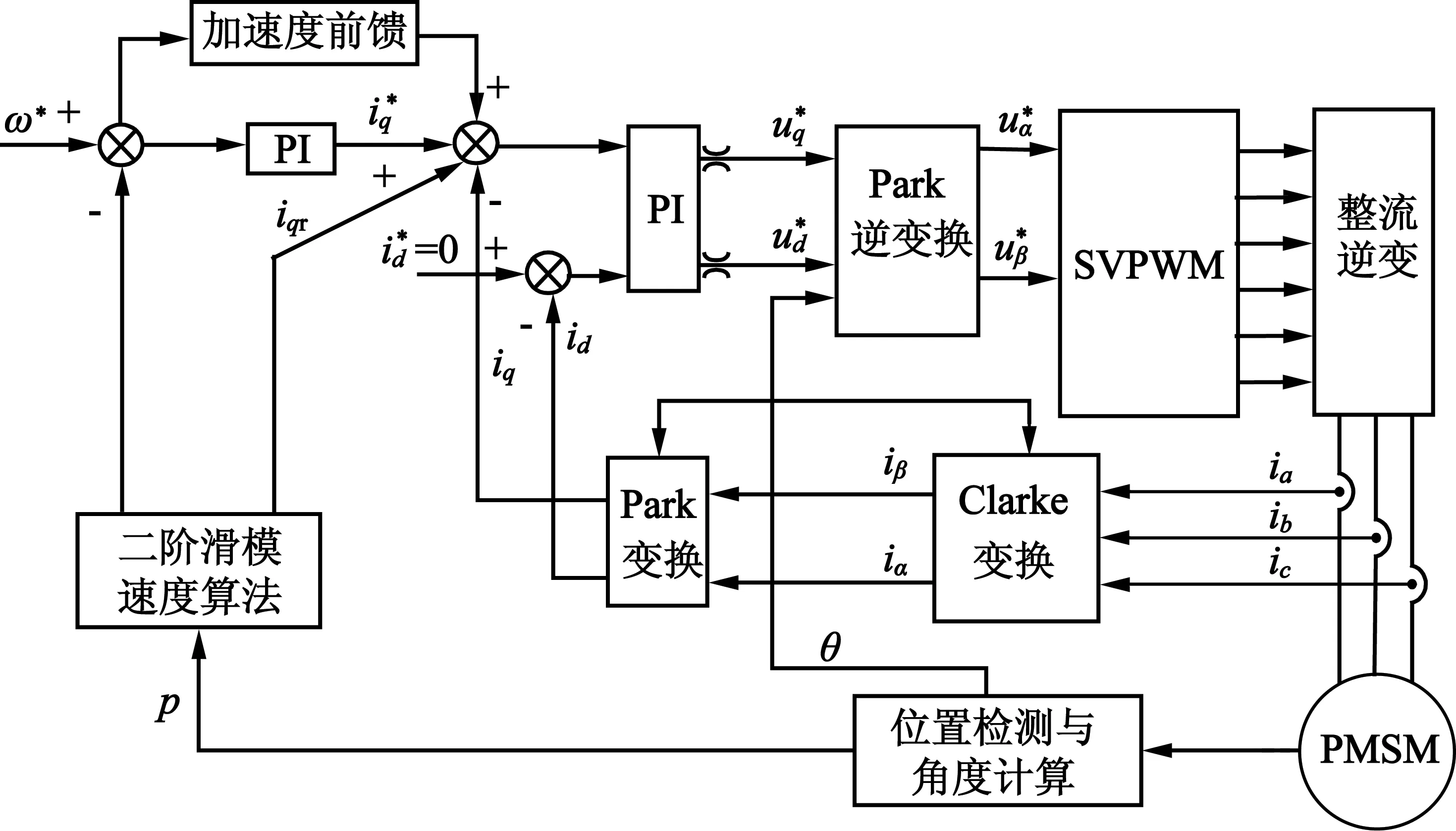
图3 基于二阶滑模算法的电机驱动系统
通过编码器对位置信号的追踪,对实际位置信号进行二阶滑模运算,得出速度值和负载转矩估计值,通过速度负反馈控制对给定速度进行调节。
用MATLAB环境下的仿真软件Simulink对上述采用二阶滑模算法控制的电机驱动系统进行仿真。仿真电机参数如下:R=2.875 Ω,Ld=Lq=8.5 mH,J=0.8×10-3kg·m2,μ=0.02 N·m·s。
图4(a)为当给定速度为1 000 r/min时采用传统的速度计算方法空载起动时速度的响应。由图4(a)可知,在空载起动时,采用传统的差分算法的系统电机起动时速度的上升时间为10.3 ms,超调量为8.6%,稳态误差为27.5~29.5 r/min。图4(b)为当给定速度为1 000 r/min时采用二阶滑模算法空载起动时速度的响应。由图4(b)可知,在空载起动时,采用二阶滑模算法的系统,电机起动时速度的上升时间为7.33 ms,几乎没有超调量,稳态误差也很小。图5为采用二阶滑模算法时的空载起动速度响应局部放大。由图5可知,采用二阶滑模算法的系统电机速度的稳态误差为17.9~21.5 r/min。

(a) 传统的速度计算方法
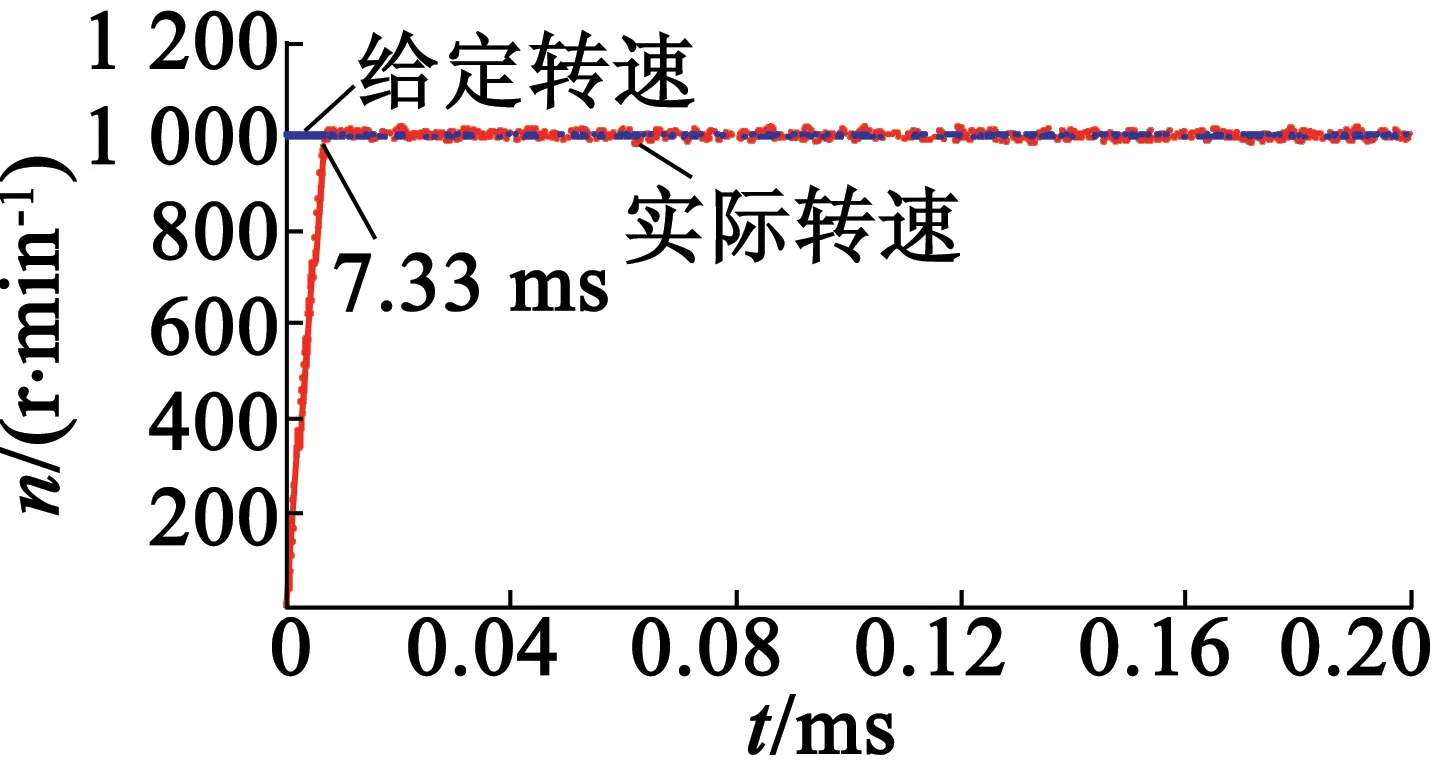
(b)二阶滑模算法
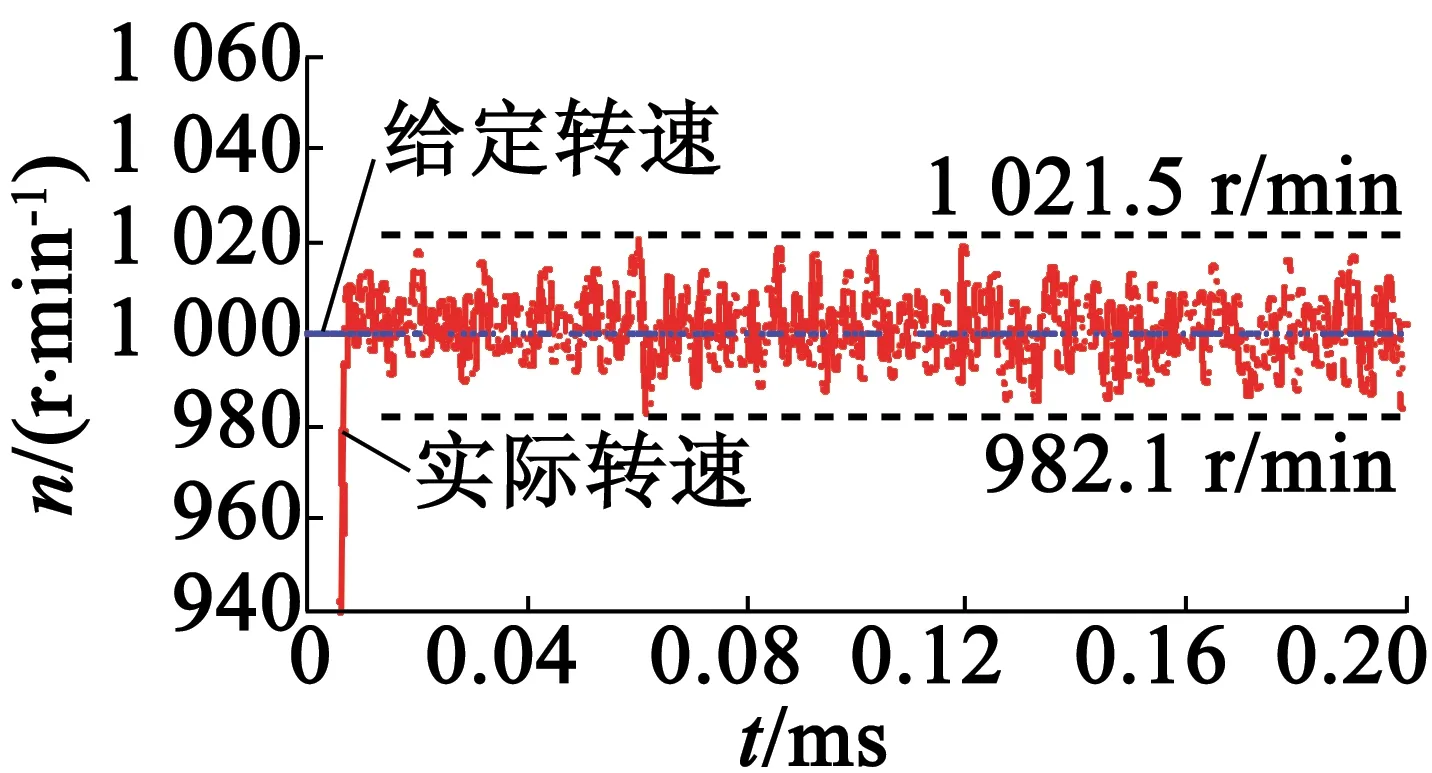
图5 采用二阶滑模算法时的空载起动速度响应局部放大
由上述数据可以明显看出,传统的电机系统波形上升时间较大,超调量较大,电机起动时间较长,稳态误差较大;而加滑模后的波形上升时间缩短,超调量变小,电机的起动时间明显缩短,稳态误差较小。这就验证了采用二阶滑模算法的交流伺服系统具有良好的鲁棒性。

图6 采用传统的速度计算方法的响应速度
图6为当系统给定速度为阶跃信号时采用传统的速度计算方法的响应速度。由图6可知,系统速度给定值从1 000 r/min至2 000 r/min的阶跃信号。在0.05s时,给定速度由1000r/min上升至1 500 r/min;在0.1 s时,给定速度由1 500 r/min上升至2 000r/min;在0.15s时,给定速度由2000r/min下降至1 000 r/min,电机的速度随着系统给定的速度的改变而改变。图7为采用传统的速度计算方法的响应速度的局部放大。由图7(a)可知,当电机速度由1 000 r/min上升至1 500 r/min时,所需时间为3.7ms,达到1 500r/min时的稳态误差为18.5~52.5 r/min。由图7(b)可知,当电机速度由1 500 r/min上升至2 000 r/min时,所需时间为3.5 ms,达到2 000 r/min时的稳态误差为22~22.9 r/min。由图7(c)可知,当电机速度由2000r/min下降至1 000 r/min时,所需时间为5.5 ms,达到1 000 r/min时的稳态误差为28.8~42.6 r/min。
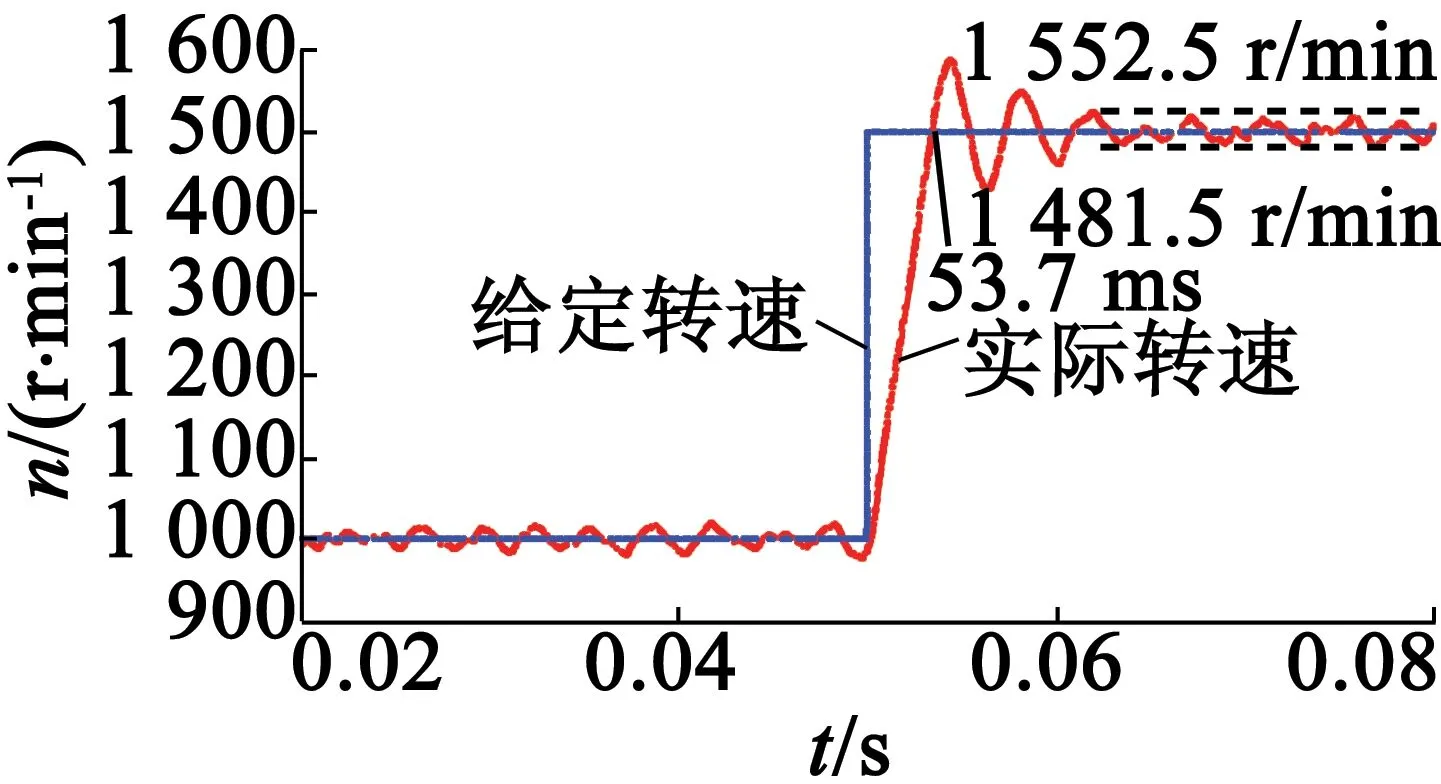
(a)1 000 r/min~1 500 r/min

(b)1 500 r/min~2 000 r/min

(c)2 000 r/min~1 000 r/min
图8为当系统给定速度为阶跃信号时采用二阶滑模算法的响应速度。由图8可知,电机的速度随着系统给定的速度的改变而变。图9为采用二阶滑模算法的响应速度的局部放大。由图9(a)可知,当电机速度由1 000 r/min上升至1 500 r/min时,所需时间为3.4 ms,达到1 500 r/min时的稳态误差为5.1~44.8 r/min。由图9(b)可知,当电机速度由1500r/min上升至2000r/min时,所需时间为3.3ms,达到2 000 r/min时的稳态误差为14.5~17.8 r/min。由图9(c)可知,当电机速度由2 000 r/min下降至1 000 r/min时,所需时间为5.7 ms,达到1 000 r/min时的稳态误差为12.9~17.6 r/min。
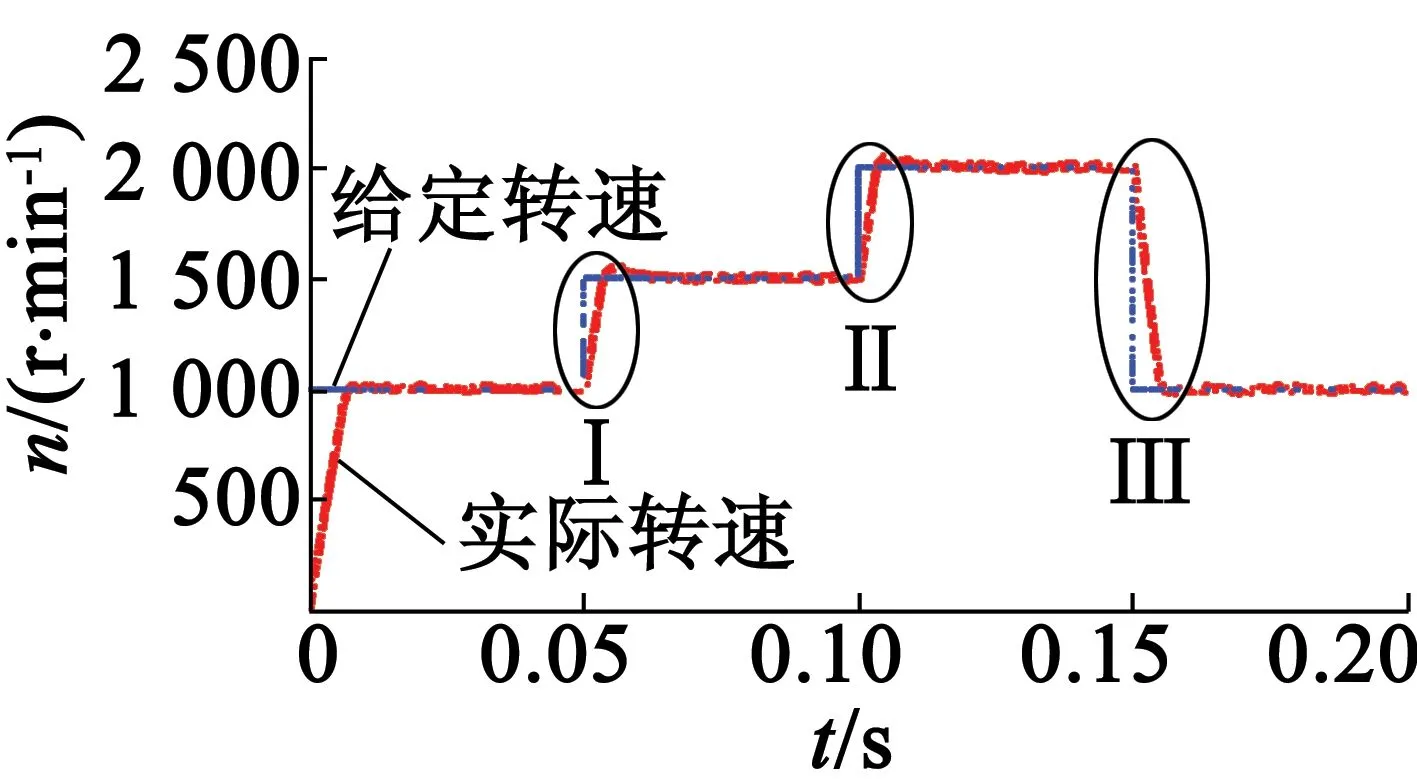
图8 采用二阶滑模算法的响应速度
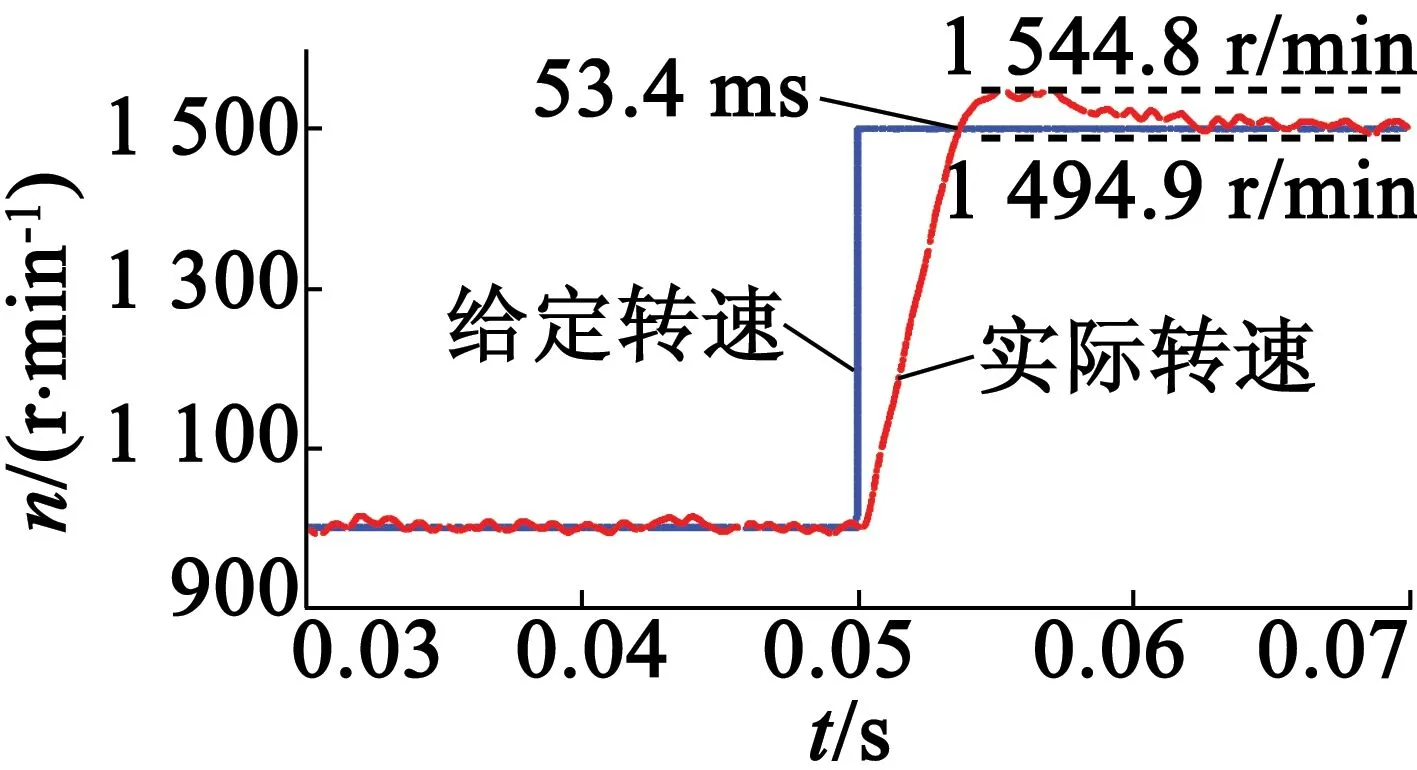
(a)1 000 r/min~1 500 r/min
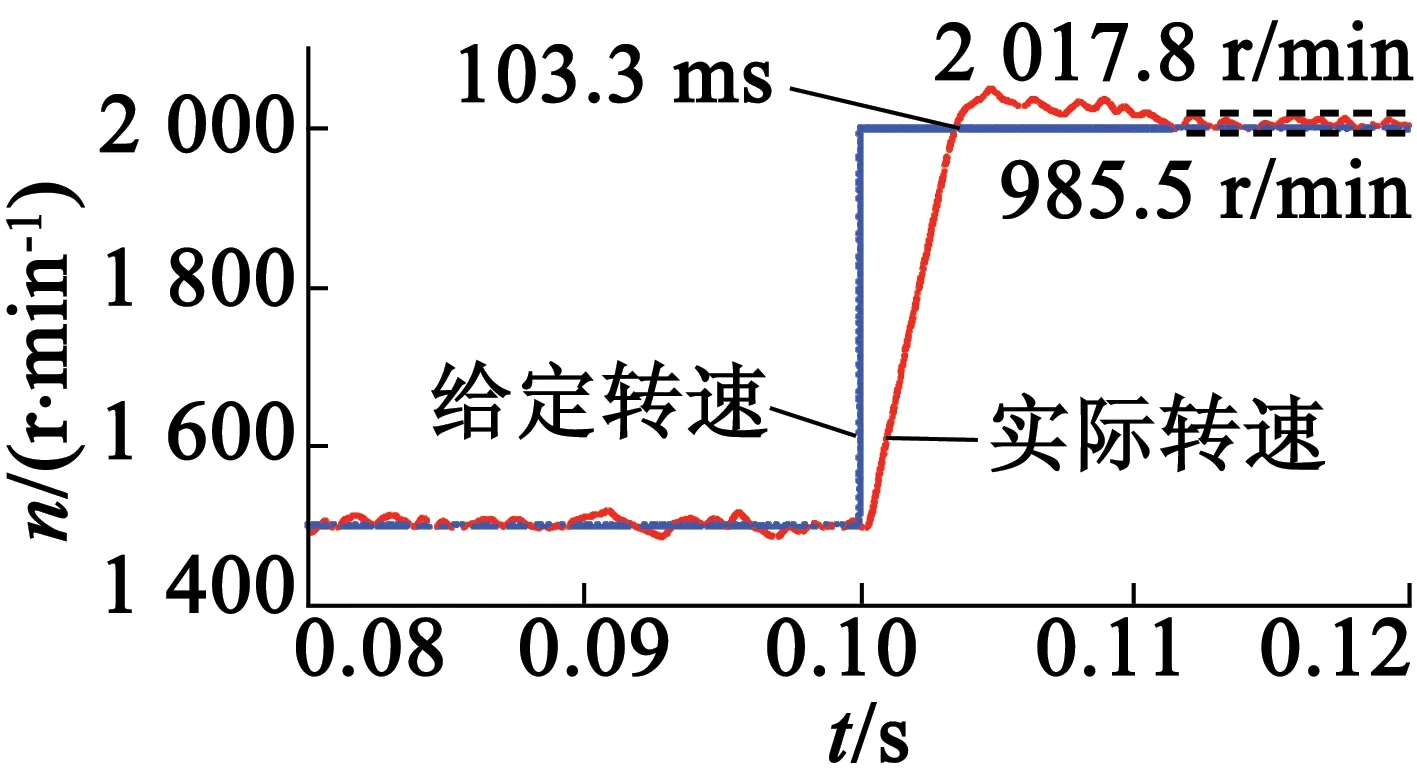
(b) 1 500 r/min~2 000 r/min

(c)2 000 r/min~1 000 r/min
由图7和图9的数据可以明显看出,传统的电机系统波形上升时间较大,稳态误差较大;而加滑模后的波形上升时间缩短,稳态误差较小。这说明了采用了二阶滑模算法后的伺服系统,具有良好的速度跟踪性能。
图10(a)为当负载在0.05 s时由1 N·m变化为2 N·m时,采用传统的速度计算方法时速度的响应。由图10(a)可知,当负载变化时,采用传统的差分算法的系统,电机恢复到稳态速度的时间为8.6 ms,超调量为5.3%。图10(b)为当负载在0.05 s时由1 N·m变化为2 N·m时,采用二阶滑模算法时速度的响应。由图10(b)可知,当负载变化时,采用二阶滑模算法的系统,电机恢复到稳态速度的时间为8 ms,超调量为3.9%。

(a) 传统的速度计算方法

(b) 二阶滑模算法
由图10的数据还可以看出,负载转矩变化时,传统差分算法的系统抖动较明显,超调量较大,长时间才能恢复系统的稳定;而采用二阶滑模算法的系统,其速度的鲁棒性和动态性能均有明显提高。
4 结 语
本文介绍了一种二阶滑模算法方法。根据二阶滑模算法的原理,通过对实时位置信号进行采样,经过二阶滑模算法得到加速度,进而得到速度值,使速度反馈值能够快速跟踪负载的变化,从而能够获得良好的动态性能。仿真结果表明,该方案具有良好的动态性能,而且对电机参数依赖性小,具有较好的鲁棒性和抗干扰性,有效地减少了系统运行过程中产生的抖动,提高了伺服系统的稳态性能。
[1] 张鹙娜,许翔军,林晓梅.基于二阶滑模的永磁同步电机直接转矩控制[J].微电机,2010,43(10):33-35.
[2] 鲁义宽.基于二阶积分滑模的永磁同步电动机速度控制方法[J].微特电机,2015,43(9):66-69.
[3] 常雪剑,刘凌,崔荣鑫.永磁同步电机非奇异快速中断可变边界层滑模控制[J].西安交通大学学报,2015,49(6):53-59.
[4] 陈伯时,陈敏逊.交流调速系统[M].北京:机械工业出版社,2006.
[5] TRZYNADLOWSKI A M.异步电机的控制[M].李鹤轩译.北京:机械工业出版社,2003.
[6] HAN Dong,LI Chun-Ru.Sliding-mode observers for systems with unknown inputs and measurement disturbances[J].Journal of Chongqing University (English Edition),2015,14(2):63-72.
[7] 唐广雪, 朱学忠,张 磊.基于SMO的开关磁阻电机无位置传感器控制仿真研究[J].机电工程,2016,33(3):303-307.
[8] BARTOLINI G,PISAN A,PUNTA E,etc.A survey of applications of second order sliding mode control to mechanical systems[J].International Journal of Control, 2005,76(9):875-892.
[9] 张晓光, 孙力, 陈小龙, 等.基于二阶滑模观测器的永磁同步电机无位置传感器控制[J].电力自动化设备,2013,33(8):36-41.
[10] JI K H,SHEN J X,JIN M J.Low speed servo system with second-order sliding mode algorithm[C]//Proceeding of the 2012 IEEE International Symposium on Industrial Electronics,Hangzhou,P.R.China,2012(5):686-691.
[11] LEVANT A.Principles of 2-sliding mode design[J].Automatica,2007,43(4):576-586.
[12] BARTOLINI G,DAMIANO A.Robust speed and torque estimation in electrical drives by second-order sliding modes[J].IEEE Transactions on Control System,2003(11):84-90.

