永磁同步电动机电流环分数阶滑模控制研究
钱春贵,左付山
(1.扬州工业职业技术学院,扬州 225000; 2.南京林业大学,南京 210037)
0 引 言
永磁同步电动机是一种强耦合、非线性系统,传统的PI控制精度不高,对于电机内外部参数扰动的鲁棒性不强。滑模控制器可以较好地克服以上不足,但滑模的抗干扰能力是通过切换项来实现的[1],大的切换增益可以加快滑模的运动速度,但是到达切换面时系统的抖振会加剧;小的切换增益引起的抖振小,但是响应的速度较慢。由于抖振问题的存在,滑模控制的应用受到了限制。
为了降低滑模控制的抖振现象,许多学者做了相关研究,例如SLOTINE J J等引入了“准滑动模态”和“边界层”的概念,用饱和函数代替切换函数,有效地消减了系统抖振。CHUNG S CY 采用Sigmoid连续函数代替切换函数来降低抖振。针对永磁同步电动机的电流环,金宁治等人提出了利用交直轴电流的积分滑模面函数作为调度变量,在允许边界范围内对切换增益系数进行调度,有效地消弱了系统的抖振[2]。张碧陶、皮佑国等人针对永磁同步电动机速度环控制[3]提出了分数阶切换滑模面结合模糊推理算法实现了软开关切换增益的自整定,有效地降低了系统的抖振。宋申民、邓立为等人提出了分数阶等速趋近律,并将其用在了航天器姿态调整中,取得了较好的控制效果[4]。陈宁、顾文军等人提出了分数阶变阶次指数滑模趋近律,将其成功应用于Lorenz混沌同步控制中[5]。本文受到以上文献的启发,提出了分数阶变阶次等速滑模趋近律,并将其用于永磁同步电动机的电流环,利用分数阶微分方程对等速趋近律增益系数进行“放大”和“缩小”,远离滑模面时对趋近律增益进行放大以加快响应速度,靠近滑模面时对趋近律增益进行缩小从而对滑模中的抖振进行抑制,同时还保持了传统等速趋近律滑模的控制效果。
1 分数阶理论
1.1 分数阶微积分定义
在1695年LEIBNIZ G W和HOSPITAL L讨论了1/2阶导数与微分的问题[6],发展到今天分数阶理论已经被广泛用于科学各领域[7]。
分数阶微积分可以看作整数阶微积分运算的一种拓展,有多种定义方法:Grunwald-Letnikov,Riemann-Liouviue,Caputo等。以Caputo型微积分为例,其定义如下[8]:
Caputo微分定义:
Caputo积分定义:
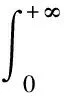
可以证明,对于很广的一类函数来讲,Grunwald-Letnikov定义和Riemann-Liouville定义是完全等效的。Caputo定义更加适合于分数阶微分方程初值问题描述,同时它对常数的求导是有界的。
1.2 分数阶微积分滤波算法
根据介绍的分数阶微积分的各种定义,需要函数f(t)为已知函数,但在控制系统中,系统内部的解析表达式通常是不知道的,所以一般转换为其他方式来求解分数阶微积分的值,例如通过构造滤波器的方式来对信号进行数值微分,文献[9]中列举了多种连续滤波器的实现方法,本文选用其中的Oustaloup算法[10]。
2 永磁同步电动机数学模型
永磁同步电动机在d-q坐标系下的定子电压方程:
式中:ud,uq为d,q轴定子电压;id,iq为定子d,q轴电流;R为定子相绕组电阻;Ld,Lq为d,q轴电感;ωe为转子的电角速度;ψf为永磁体磁链。
电磁转矩方程:
式中:Te为电磁转矩;p为电机的极对数。
运动方程:
式中:J为转动惯量;ωm为转子的机械角速度;ωe=pωm;B为摩擦系数;TL为电机的负载转矩。
3 电流控制器设计
令ed=idr-id,eq=iqr-iq,建立d,q轴的电流误差状态方程[11]。
(1)
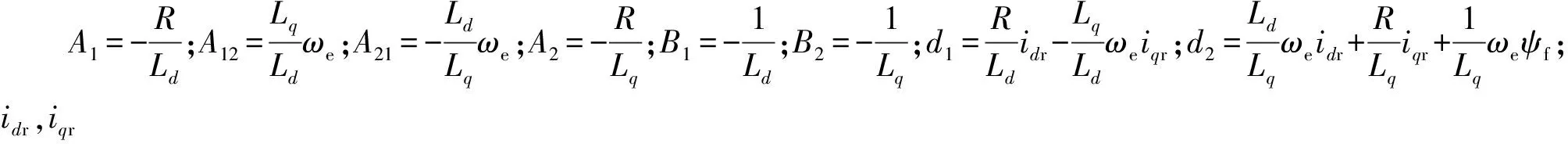
考虑到电机电阻、电感、磁链等参数变化对电流环控制系统的影响,选取积分滑模面:
(2)
式中:sd,sq为d,q轴滑模面,c1,c2为大于0的实数。
趋近律方法可以有效改善滑模运动的动态品质,常用的趋近律有幂次趋近律、等速趋近律、指数趋近律等。与其他形式的趋近律相比,等速趋近律具有结构简单、更加容易实现的优势[12],所以本文以等速趋近律为基础,将其改造为分数阶等速趋近律。
对于d,q轴电流控制系统,分数阶等速趋近律表示:
(3)
与传统的等速趋近律相比,分数阶等速趋近律在原有基础上多了一个可调参数α,这样可以改变系统到达滑模面的速度,从而改变系统的抖振。
对式(3)两边进行求导得:
(4)
利用Oustaloup滤波器方法进行分数阶求解α分别为0.85和1.05时D1-αsgn(s)的值,结果如图1所示。

图1 sgn(s)函数的D1-0.85,D1-1.05次导数的值
随着时间t的变化,滑模面s在一定的范围内变化,根据符号函数sgn(s)的定义:s>0时,sgn(s)=1;s<0时,sgn(s)=-1;s=0时,sgn(s)=0。所以随着时间t的变化sgn(s)的值始终在-1,0,1之间进行变化。当α=0.85时,D1-0.85sgn(s)的值如图1中点划线所示,此时分数阶求导后存在|D1-0.85sgn(s)|﹥|sgn(s)|,起到了“放大”作用;当α=1.05时,D1-1.05sgn(s)的值如图1中虚线所示,此时分数阶求导以后存在|D1-1.05sgn(s)|﹤|sgn(s)|,起到了“缩小”增益系数的作用。此外可以发现sgn(s),D1-0.85sgn(s),D1-1.05sgn(s)三者的符号是一致的,可以证明存在如下等式[13]:
sgn[Dγsgn(s)]=sgn(s),-1<γ<1
由上式可得:
D1-αsgn(s)=|D1-αsgn(s)|sgn(s) 0<α<2
在等速滑模控制中,当远离滑模面时我们希望趋近滑模面的速度快一些,即增益ε1,ε2大一些;当接近滑模面时,希望趋近的速度慢一些,即增益ε1,ε2小一些,以便尽量减小系统抖振。利用分数阶等速趋近律ε1D1-αsgn(s),ε2D1-αsgn(s),可以通过控制分数阶导数的阶次α随着滑模面s值的变化进行变化,从而对增益ε1,ε2进行“放大”和“缩小”,以满足远离滑模面时加快趋近速度,靠近滑模面时降低速度减小抖振的要求。
将d1,d2作为扰动,同时满足|d1|≤d1max,|d2|≤d2max,根据式(1)、式(2)、式(4)可得电流控制律:
选择Lyapunov函数:
则存在:
根据Lyapunov函数稳定性判据,当ε1|D1-α·sgn(sd)|-d1﹥0,ε2|D1-αsgn(sq)|-d2﹥0时可以满足滑模存在性和可达性条件。
4 仿真分析
本文以表贴式永磁同步电动机为研究对象,采用id=0控制策略,在MATLAB/Simulink环境下建立了永磁同步电动机矢量控制模型,并进行了仿真研究,其具体结构如图2所示,外环速度环采用传统的PI控制器,内环电流环换成了变阶次分数阶滑模控制器。

图2 伺服系统仿真平台
经过反复试验,本文以滑模面s的绝对值作为分数阶等速趋近律阶次切换的判断依据,当滑模面s的绝对值接近稳定状态0时,分数阶的阶次α取1.05,反之分数阶的阶次α取0.85。
永磁同步电动机的主要参数[14]:功率为1.1 kW,额定电压为220 V,额定转速为3 000 r/min,额定扭矩为3.5 N·m,相电阻为2.875 Ω,d,q轴电感为0.008 5 H,永磁体磁链为0.175 Wb,转动惯量为0.008 kg·m2,极对数为4。
控制参数如下:速度环比例、积分系数分别为0.023,0.25。电流环d,q轴等速趋近律增益系数分别为1,23 529,滑模面积分系数均为3.5。
考虑到电机转速在基速以上时涉及到弱磁控制,本文目前只讨论目标转速在基速以下时电流环的跟踪效果和电机的转矩输出情况。电机的初始负载设定为1 N·m,目标转速设定为1 000 r/min,在t=0.5 s时突加负载至2 N·m,目标转速始终保持在1 000 r/min。
图3为电机转速响应图,图中实线为传统等速趋近律控制,点横线为变阶次分数阶等速趋近律控制。从仿真结果来看,初始时刻快接近稳定状态时,两者的差值始终在±1 r/min内,0.5 s时刻突加负载时,两者的误差始终在±0.8 r/min内,所以变阶次分数阶等速滑模基本保留了传统等速滑模的控制效果。

图3 永磁同步电动机转速响应图
图4是图3相对应的电流状态收敛轨迹。图中横坐标为切换面s,纵坐标为切换面变化率ds。图中实线部分为传统整数阶等速趋近律滑模控制电流收敛轨迹,点横线为变阶次分数阶等速趋近律电流环误差收敛轨迹。在整个运动过程中,分数阶的抖振幅值分为两个部分,为了保证系统的快速响应能力,在远离滑模面时采用的分数阶的阶次α=0.85,此时的抖振如图4所示,其幅值大于整数阶等速趋近律幅值;当靠近滑模面时采用的分数阶的阶次α=1.05,系统最终达到平衡状态,稳定在这个幅值,此时的抖振幅值是低于整数阶抖振的幅值,降幅达到了28.7%,实现了降低电流环抖振幅值的目的。

图4 两种滑模控制系统电流收敛轨迹
图5是图3相对应的永磁同步电动机转矩响应图,虚线为传统整数阶等速趋近律,实线为分数阶转矩响应。在0.5 s时负载由1 N ·m增加至2 N ·m。从图5中可以看出,变阶次分数阶等速趋近律转矩输出的脉动程度低于整数阶等速趋近律,平均降幅可达到5.3%,进一步证明了变阶次滑模在降低电流环抖振方面的作用。
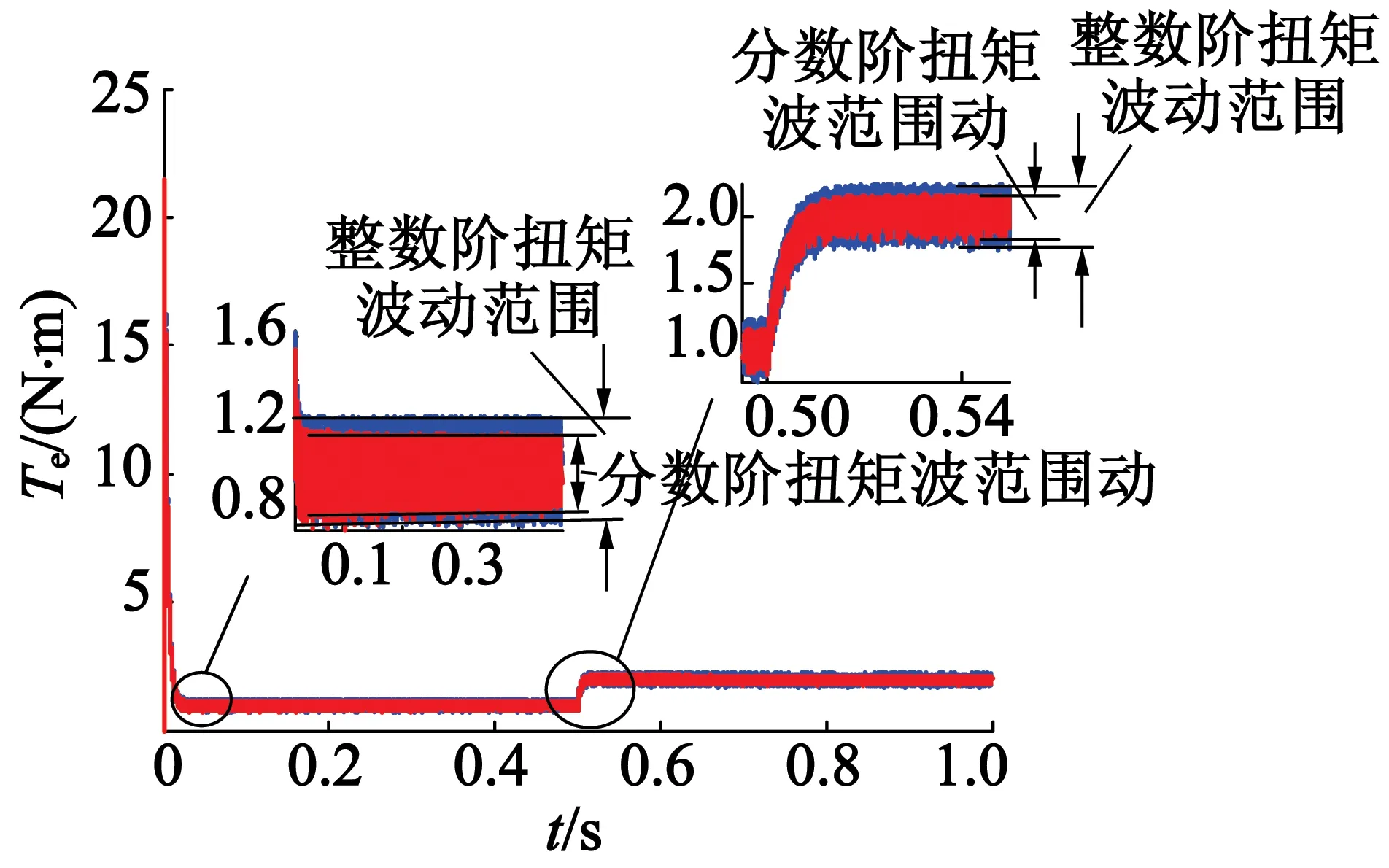
图5 电机转矩响应轨迹
5 结 语
本文针对等速趋近律滑模变结构在永磁同步电动机电流环控制中的抖振现象,提出了一种变阶次分数阶等速滑模控制,利用分数阶微分方程对等速趋近律增益系数进行“放大”和“缩小”,远离滑模面时对趋近律增益进行放大以加快响应速度,靠近滑模面时对趋近律增益进行缩小以抑制抖振。在Simulink环境下建立了矢量控制模型进行仿真研究,在基速以下进行了仿真研究。仿真结果表明,本文的控制方法在保留传统方法控制效果的同时,在一定程度上减小电流环的抖振幅值,降低电机转矩输出脉动的程度,达到了良好的控制效果。
[1] 卢涛,于海生,山炳强,等.永磁同步电机伺服系统的自适应滑模最大转矩/电流控制[J].控制理论与应用,2015,32(2):251-255.
[2] 金宁治,张忠民,刘瑞增.具有增益调度切换增益的永磁同步电机滑模控制[J].电气传动,2015,45(4):3-7.
[3] 张碧陶,皮佑国.基于分数阶滑模控制技术的永磁同步电机控制[J].控制理论与应用,2012,29(9):1193-1197.
[4] 宋申民,邓立为,陈兴林.分数阶微积分在滑模控制中的应用特性[J].中国惯性技术学报,2014,22(4):439-444.
[5] 顾文军.Lorenz混沌电路的分数阶控制[D].南京:南京林业大学,2012:33-42.
[6] CHEN Yangquan,LUO Ying .Discussion on:“Simple Fractional Order Model Structures and their Applications in Control System Design”[J].European Journal of Control,2010,6:695-699.
[7] OUSTALOUP A,SABATIER J,LANUSSE P.From fractional robustness to CRONE control[J].Fractional Calculus and Applied Analysis,1999,2(1):1-30.
[8] PODLUBNY I.Fractional differential equations[M].San Diego:Academic Press,1999.
[9] PETRAS I,PODLUBNY I,O’Leary Petal.Analogue Realization of Fractional Order Controllers[J].Fberg Technical University of Kosice Kosice Slovak Isbn Edition,2002,29(1-4):281-296.
[10] OUSTALOUP A,LEVRON F,MATHIEU B,et aL.Frequency-band complex noninteger differentiator:characterization and synthesis[J].IEEE Transaction on Circuit and Systems-I:Fundamental.Theory and Applications,2000,47(1):25-39
[11] 金宁治,王旭东,李文娟.混合动力汽车永磁同步电机的电流滑模控制与负载扰动补偿[J].汽车工程,2013,35(6):554-558.
[12] 米阳,潘达,吴晓.基于等速趋近律的滑模负荷频率控制设计[J].控制工程,2014,21(3):327-329.
[13] EFEMÖ.Fractional fuzzy adaptive sliding-mode control of a 2-DOF direct-drive robot arm[J].IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society,2008,38(6):1561-1570.
[14] 董恒,王辉,黄科元.永磁同步电机驱动系统数字PI调节器参数设计[J].电气传动,2009,39(1):7-10.

