新型混合式高效永磁调速器温度场仿真与分析

刘 岩，高庆忠，王 森，赵阳阳，郭 枫

(1.辽宁轨道交通职业学院，沈阳 110023；2.沈阳工程学院，沈阳 110136)

0 引 言

永磁调速器是一种电力传动的机械装置，主要由铜盘转子、永磁盘转子和执行机构组成，用于恒速电机和负载之间，可利用执行机构自动或手动调节气隙大小，从而完成传输转矩和转速的控制。永磁调速器实际工作时，铜盘相对磁盘旋转，铜盘内产生涡流电场而在气隙中产生感应电场，该感应电场与永磁盘磁场共同作用，使其表现电磁驱动特性。由于本身具备的非接触结构，使其具有软启动、高效节能、无谐波干扰、对中误差允许高、过载保护和使用寿命长等特点，目前已广泛应用到石油、化工和电力系统等领域。

在永磁调速器研究上，国内外专家学者已取得诸多研究成果。CANOVA A等人设计了一种盘式永磁调速器，完成盘式解析模型的推导，通过有限元分析方法验证解析方法正确性[1]。TONOLI A等人建立磁力耦合器数学模型，给出理论设计方法和转矩性能曲线[2]。CHA H-R等人研究永磁体充磁方向对永磁调速器性能影响，通过有限元方法研究不同充磁方向下的输出转矩特性曲线[3]。LUBIN T L等人研究盘式永磁调速器静态和瞬态特性，给出输出转矩解析方程，完成有限元仿真分析和实验验证[4]。王旭等人研究永磁调速器磁路结构设计，分析磁路的形成机理和耦合原理，完成永磁调速器涡流场分析，获得涡流场的分布并对涡流进行了参数化分析[5-6]。徐伟等人对永磁调速器的涡流场进行了分析[7]。刘伟等人采用有限元方法完成永磁调速器磁场和转矩特性分析，给出了传动效率的计算方法[8-9]。孙中圣等人对筒式永磁调速器磁场和特性分析与研究[10]。

目前对于永磁调速器的研究多集中在基于盘式或筒式单一结构下的磁场和涡流场分析上。本文提出一种混合式永磁调速器结构，这种混合式结构既具有径向磁路，又具有轴向磁路，可增大永磁调速器的转矩和功率密度。但这种混合式结构增加了电涡流密度，使得单位体积内的散热量上升，因此应重点研究温升分布和散热问题，防止永磁体退磁。对于永磁调速器温度场研究，多集中在有限元数值方法研究，采用电磁和热耦合方法进行温度场仿真分析[11-12]。

本文基于混合式永磁调速器的物理模型，流体力学和传热学理论，建立混合式永磁调速器三维温度场求解的数学模型。进行混合式永磁调速器传热分析和损耗分析，给出温度场求解的过程，完成混合式永磁调速器温度场模型建立，仿真分析和温升实验测试。

1 混合式永磁调速器模型建模

混合式永磁调速器主要由径向永磁体、轴向永磁体、径向铜环、轴向铜盘等构成，具有轴向和径向混合励磁磁路结构。设计的混合式永磁调速器额定功率10 kW，额定转矩65.4 N·m，图1给出混合式永磁调速器的仿真模型。为增加其散热能力，分别在径向环形外壳和轴向壳体右侧装设散热筋。

图1 混合式永磁调速器仿真模型

混合式永磁调速器的径向结构和轴向结构可细分为钢盘、铜盘、永磁体、隔磁铝盘、支撑架等部件，具体的结构尺寸如表1所示。

表1 混合式永磁调速器参数

其中，轴向永磁侧钢盘内外径尺寸和轴向导体侧相同。钢的材料为45号钢，铜的材料为2H62，永磁材料为N40SH。

2 混合式永磁调速器数学模型

根据流体力学和传热学原理，混合式永磁调速器满足质量守恒定律、动量守恒定律和能量守恒定律。本文建立的混合式永磁调速器的温度场数学模型如下：

(1)

式中：ρ为流体密度；u，v和w分别为速度矢量在x，y和z方向的分量。

(2)

式中：μ为流体运动黏度，固体的运动黏度为无穷大；p为流体压力；Fx，Fy和Fz分别为作用在流体上的质量力F在x，y和z方向的分量。

(3)

式中：T为流体温度；U为流体速度矢量；cp为比热容；ST为流体的内热源及由于粘性作用流体机械能转化为热能的部分。

对于混合式永磁调速器气隙求解区域中的流体运动，考虑模型复杂度和计算效率，可采用标准k-ε模型计算，该模型对于管流，通道流通，二维和三维无旋和弱旋加流流动具有较高计算精度。具体的模型表述如下：

(4)

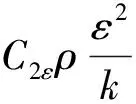
(5)

式中：k为流体湍流动能；ε为流体湍流动能的耗散率；μt为湍流粘度；Gk为平均速度梯度引起的湍动能k的产生项；Gb为浮力引起的湍动能k的产生项；C1ε，C2ε，σk，σε为经验系数。

3 温度场数值求解条件

3.1 基本假设

对混合式永磁调速器温度场数值求解作如下假设：

(1)不考虑导体盘集肤效应的影响，导体盘热源分布均匀；

(2)永磁调速器各部件使用各项同性导热系数；

(3)永磁调速器导磁材料如钢盘没有发生饱和现象，永磁调速器导体铁心均匀磁化；

(4)忽略永磁调速器内部电磁波的热辐射作用；

(5)只考虑永磁调速器外表面与空气的对流换热，不考虑外部散热环境的变化。

3.2 传热分析

混合式永磁调速器气隙中空气的导热系数与空气的流动方式有关，空气的流动方式又与永磁调速器的结构尺寸、转动速度与气隙厚度等有关。为简化分析计算，引入有效导热系数，将转子与气隙之间复杂的对流散热方式等效为静止流体的导热方式换热，有效导热系数：

(6)

式中：λg为气隙的有效导热系数；Reg为气隙雷诺数；n1为导体盘和永磁盘的相对转速；γ为空气运动粘度，正常工作时取γ=1.48×10-6；D为永磁转子外径；Dw为导体转子内径；λD为直径比；Recr为临界雷诺数。

3.3 损耗分析

(1) 涡流损耗

涡流损耗主要由永磁调速器导体盘因电涡流效应而产生的热损耗和导磁材料中由于交变磁场而产生的沿磁场垂直方向的涡流损耗。导体盘中的电涡流损耗计算公式：

(7)

式中：ρ为导体盘电阻率；J为导体盘电流密度；V为导体盘体积。

导磁材料中的涡流损耗计算如下：

pe2=Kef2B2

(8)

式中：Ke为涡流损耗系数；f为导体转子相对永磁转子的磁场交变频率；B为导体盘上的磁通密度。

(2) 磁滞损耗

磁滞损耗主要发生在轴向和径向钢盘或钢环中，当永磁调速器永磁转子和导体转子有一定转差时，导磁盘内存在一个交变磁场，会在导磁盘内产生磁滞损耗，可用下式计算：

(9)

式中：Kh为磁滞损耗系数；K(ΔBT)为总磁滞损耗修正系数；K(ΔBT)=1+KminΔBT；ΔBT为每周期内局部磁场密度反复变化相对磁密幅值作用的总和。

混合式永磁调速器的总损耗：

p=pe1+pe2+ph

(10)

4 温度场仿真分析

4.1 三维温度场求解过程

本文采用有限元方法完成混合式永磁调速器的三维稳态温度场分析，求解过程主要包括稳态温度场分析、混合式永磁调速器建模、永磁调速器材料添加、热源设置、网络剖分、散热系数设置、求解器求解和模型后处理。具体求解步骤如图2所示。

图2 温度场分析求解过程

4.2 三维模型建立

确定混合式永磁调速器的热源及相关热参数后，为深入研究其永磁调速器整体及局部温度分布情况，本文利用有限元方法对混合式永磁调速器的三维稳态温度场求解。

混合式永磁调速器的导体转子包括永磁调速器前端盖、后端盖、轴向铜环、径向铜环、外壳和散热筋。永磁转子包括轴向永磁体盘、径向永磁体盘、隔磁桥、固定盘和连接轴等部件。对混合式永磁调速器模型整体剖分，剖分精度为2 mm，整个仿真模型有23 561个剖分单元。

4.3 混合式永磁调速器温度仿真分析

图3为混合式永磁调速器的永磁转子整体温度分布。能看出在满载状态下运转时，整体永磁转子的最高温度处在轴向永磁体上，最高温度为92 ℃。永磁转子转轴的温度较低，说明轴承温升处于允许范围内。

图3 整体温度分布

对于混合式永磁调速器的铜盘的热分析，当交变的磁场通过铜盘时，会在铜盘上产生电涡流。电涡流在磁场的作用下大部分会产生电磁驱动效果，实现力矩的无接触传递；少部分会以热量的形式散发掉。

图4是轴向铜盘的温度分布图，最高温升集中在内圆环1/5～2/3之处，最高温度与达到107 ℃，这个范围内的圆环区域是磁场交变的重点区域。从温度分布中可清晰看出，铜环外端部比中心区域温度低，这是由于铜盘沿轴向的传热能力比径向好，且外部铜环与转子外壳距离较近，热传导系数和散热系数较好。

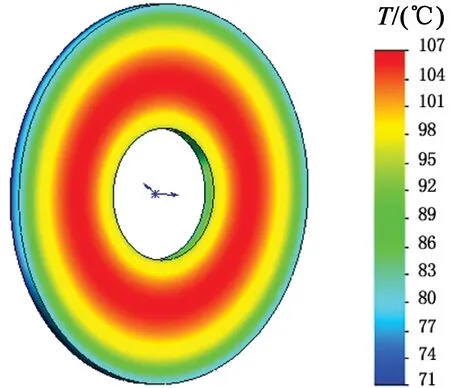
图4 轴向铜盘温度分布

图5为混合式永磁调速器径向铜盘的温度分布图。径向铜盘最低温度集中在铜盘内环，温度最高的地方集中在外环，温度在外环由中间向两端递减。其中，径向铜环最高温度为96 ℃。

图5 径向铜盘温度分布

4.4 散热筋对温度场的影响分析

图6和图7给出混合式永磁调速器外壳无桶筋和有桶筋的温度分布仿真图。可看出，混合式永磁调速器轴向结构加有散热筋，轴向铜盘上的热量可通过外壳和轴向散热筋散发，其径向散热筋温度最高为57 ℃。而对于无径向散热筋结构，径向外壳最高温度达到67 ℃。相比而言，径向结构增加5 mm的散热筋，其温度由原来的67 ℃降到50 ℃左右，降低25.4%，降温效果明显。

图6 外壳无桶筋温度分布

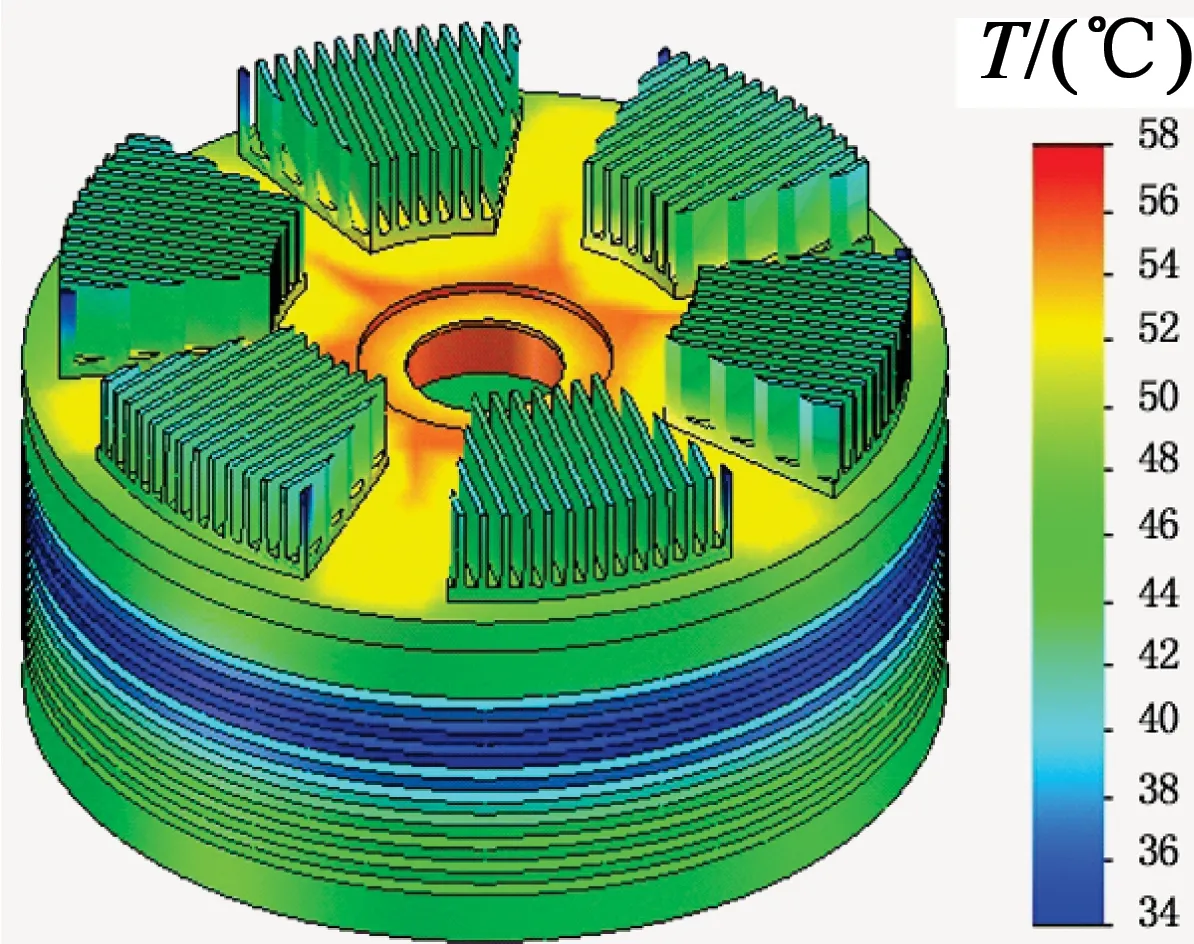
图7 外壳有桶筋温度分布

5 实验分析

本文采用温升实验平台如图8所示，主要包括异步电动机、混合式永磁调速器、电涡流制动器、制动器水冷系统、温度传感器和温度采集系统，其中，温度传感器分别置于新型混合式永磁调速器的机壳、轴向铜盘、径向铜环、轴向永磁体和径向永磁体上。

图8 混合式永磁调速器温升实验

测量混合式永磁调速器温升时，首先起动异步电动机；然后减小气隙至2 mm，使负载轴转速提高至预定转速；随后控制电涡流制动器，增大负载转矩至65.4 N·m。运行一段时间，等温升稳定后分别记录机壳，轴向铜盘，径向铜环，轴向永磁体和径向永磁体的温度，得到如表2实验数据。可看出，混合式永磁调速器温升仿真值和实验值基本一致；其中误差最大的部件为机壳，最大误差为6.7%，误差最小的部件为轴向铜盘，最小误差为3.2%。

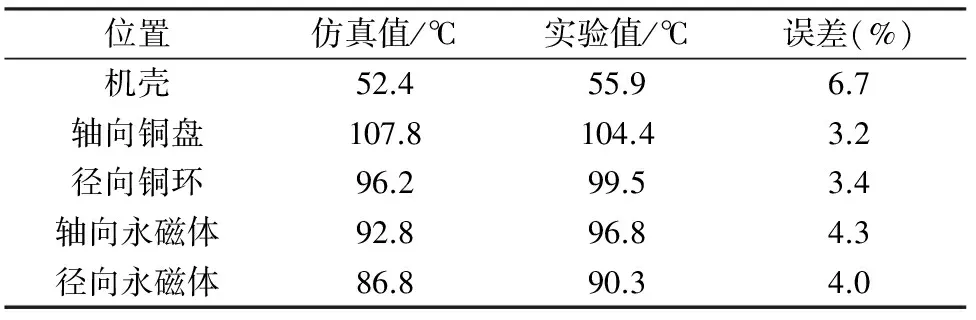
表2 实验数据

6 结 语

本文基于混合式永磁调速器的温度场数学模型，给出混合式永磁调速器温度场求解的基本假设、传热分析和损耗分析，完成混合式永磁调速器温度场模型建立，仿真分析和实验验证。得到如下结论：

1) 本文的混合式永磁调速器结构，具有轴向和径向磁路结构，高的励磁密度能够提高永磁调速器的输出转矩密度。

2) 完成混合式永磁调速器整体温度场分析，对比有无散热筋对混合式永磁调速器散热的影响，得出有散热筋温度比无散热筋降低25.4%。

3) 搭建了混合式永磁调速器温度场测试实验平台，对比实验数据和仿真数据，发现温度场分析仿真值和实验值基本一致，最大误差偏离为6.7%。

[1] CANOVA A,VUSINI B.Design of axial eddy-current couplers[J].IEEE Transactions on Industry Applications,2003,39(3):725-733.

[2] TONOLI A.Dynamic characteristics of eddy current dampers and couplers[J].Journal of Sound and Vibration,2007,301(3): 576-591.

[3] CHA H R,CHO H W,LEE S H.The influence of magnetization pattern on the performance of permanent magnet eddy current couplings and brakes[J].Journal of Electrical Engineering & Technology,2008,3(3):379-384.

[4]LUBINT,REZZOUGA.Steady-stateandtransientperformanceofaxial-fieldeddy-currentcoupling[J].IEEETransactionsonIndustrialElectronics,2015,62(4):2287-2296.

[5] 王旭,王大志.永磁调速器的磁路结构设计[J].电气传动,2011,41(10):55-58.

[6] 王旭,王大志,刘震,等.永磁调速器的涡流场分析与性能计算[J].仪器仪表学报,2012,33(1):155-160.

[7] 徐伟,孙建军.永磁调速器的涡流场分析[J].机械传动,2015,39(2):115-118.

[8] 刘伟,佟强,杨帛润,等.永磁调速器的有限元分析与性能计算[J].微特电机,2015,43(4):10-13.

[9] 刘伟,郑晓娜,徐德奎.永磁调速器转矩特性与传动效率的仿真计算[J].化工自动化及仪表,2016,43(1):40-45.

[10] 孙中圣,周丽萍,王向东,等.筒式永磁调速器的磁场分析与特性研究[J].中国机械工程,2015,26(13):1742-1747.

[11] 王延杰,周三平.永磁调速器温度场仿真分析[J].科技视界,2015(9):114，159.

[12] 刘伟,佟强.基于电磁-热耦合有限元分析的永磁调速器性能研究[J].组合机床与自动化加工技术,2016(1):4-9.