整体式双层永磁体涡流联轴器的设计与研究

陈 科，马计委，郑红梅，史洪扬，殷 磊,2

(1.合肥工业大学 机械工程学院，合肥 230009；2.泰尔重工股份有限公司，安徽 马鞍山243071)

0 引 言

永磁涡流联轴器是一种在电机转子和负载之间实现动力非接触式传递的机械设备，其工作原理：主、从动盘发生相对转动，依据法拉第电磁感应定律和安培定则，铜盘内产生涡流磁场并与原永磁体磁场相互作用，从而产生电磁转矩。和传统机械连接的联轴器相比，具有环境适应性强、安装要求低等诸多优点，发展前景广阔，可适用于工业、航天等[1]诸多领域。

目前，国内外应用的永磁涡流联轴器结构主要分为两大类：轴向盘式磁通结构和径向圆筒式磁通结构。这两种结构在分析方法上有所区别，盘式结构在直角坐标系下求解转矩性能，而圆筒式是在极坐标系下求解。THIERRY[2]等研究只含有单层铜盘与单层永磁体盘的轴向盘式永磁涡流联轴器，提出一种简化的解析数学模型，并结合实验和仿真验证了模型的有效性。由于转矩性能的提升需求，近年来双层铜盘结构形式的永磁涡流联轴器得到广泛应用。对于单层永磁体双层铜盘结构的涡流联轴器：一种是ZHAO Li等[3]提出的永磁体镶嵌在轭铁中周向充磁形式的涡流联轴器，其在永磁区域利用子域法结合等效磁路法[4-5]求解切向与法向的磁源解析式，其他区域利用二维层模型的矢量磁位法进而分析转矩性能；另一种是AMGED[6]提出的中间永磁体盘为轴向充磁形式的涡流联轴器，使用混合粒子群-单纯形结合的优化法对其进行了分析。与此同时，双层永磁体结构的涡流联轴器也相继出现，李延民等[7]研究的双层永磁体结构是在传统单层永磁体单层铜盘涡流联轴器基础上进行的简单叠加，其缺点是叠加结构相对复杂且安装成本较高。韩国学者Hyeon-Jae Shin等[8]提出双层永磁体单层铜盘的结构，此结构对双层永磁体的磁感应强度的利用率有所提高，其缺点是只有单层铜盘产生转矩且单层铜盘的结构强度较弱。

综合以上情况，本文提出了整体式双层永磁体双铜盘涡流联轴器，其结构相对简单，转矩性能相对较好；双层永磁体和背铁相间排列的结构形式显著增加涡流联轴器的轴向结构刚度，这一特殊优势对多盘涡流联轴器的发展具有借鉴意义。为了分析该永磁涡流联轴器的转矩性能情况，需先利用二维层模型理论进行假设，将3D模型线性拓扑为2D模型，再采用直角坐标系下的矢量磁位法，列出各区域的拉普拉斯和泊松方程并求解；通过能量守恒法计算出铜盘转矩并将解析结果和有限元仿真结果对比验证，最终得出结论。

1 模型和假设

1.1 几何结构

整体式双层永磁体涡流联轴器的结构如图1所示，由1个主动盘(双层永磁体及背铁)和2个从动盘(铜盘及背铁)组成。图中，铜盘背铁厚度l1、铜盘厚度l2、永磁体厚度l3、永磁体背铁厚度l4、背铁孔半径R1、铜盘内、外径分别用R2、R3，永磁体盘内、外径分别为R4、R5表示。永磁体盘和铜盘之间的气隙轴向长度、磁极对数分别用g、p表示。

图1 轴向双层永磁体盘式涡流联轴器

1.2 解析假设

采用二维层模型的矢量磁位法定量分析图1所示三维结构涡流联轴器的转矩性能，为了简化分析，如图2所示，将3D模型问题转化为2D层模型问题，并作如下假设：

(1)双层铜盘及其背铁静止不动，而永磁体及其背铁以恒定速度沿x轴方向运动(x轴位于1/2永磁体背铁厚度处)。

(2)各层区域都为线性的。

(3)永磁体盘背铁的磁导率为无穷大，铜层背铁的磁导率为等效平均磁导率μeq。

(4)运动方向涉及的所有场量，都是周期对称的，并且只考虑一次谐波的影响。

图2 永磁涡流联轴器简化层模型

图2所示的Γ是指各区域(I、II、III、IV)之间的边界面，x轴展开于永磁体内、外径中心处。

2 理论分析

2.1 铜盘转矩产生原理

如图3所示，永磁体盘磁体的N极发出磁感线经空气-铜盘-铜盘背铁在相邻磁极间形成闭合磁路。磁路的走向为铜盘切割磁感线产生持续不断的转矩动力源提供了必要条件。相较于传统单层永磁体的贴装式磁体，两层永磁体的N、S极通过中间背铁相互吸引，形成整体式主动盘，加强了结构刚度。

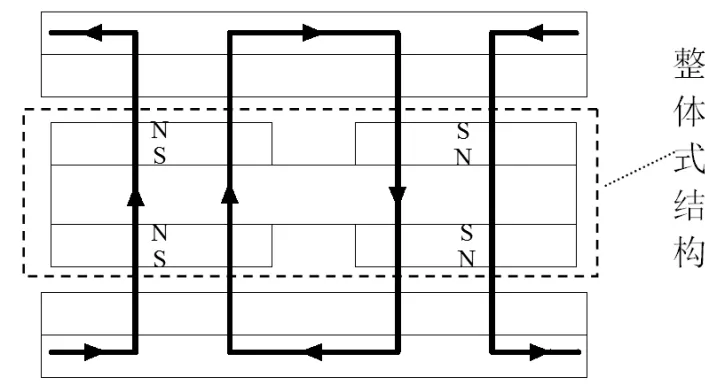
图3 永磁涡流联轴器的整体式磁路

永磁体盘上存在p对磁体，由于每对磁体对铜盘产生的转矩效果相同，故只取一对相邻磁体受力分析，如图4所示。永磁体盘及其背铁作为主动盘在以速度v运动过程中，铜盘切割磁感线并在铜盘内部产生电流，电流方向依据右手定则判定。从图4可以看出，垂直纸面向内的叉向电流与垂直纸面向外的点向电流构成的涡流回路将产生磁场，可把该涡流回路等效为永磁体，并将其定义为等效磁体。

永磁体盘上存在2p个磁体，铜盘上也会感应出2p个涡流回路且相邻涡流回路的旋向相反，这样才能保证铜盘受到相同方向的切向合力，驱动从动盘(铜盘及铜盘背铁)。因此，铜盘将会被等效为存在2p个等效磁体的等效磁体盘。至此，永磁体-铜盘之间的相互作用转化为永磁体-等效永磁体的相互作用，更易分析铜盘转矩的作用力来源。

如图4所示，等效磁体的中心为涡流回路的圆心O，涡流回路最大半径为R。等效磁体横跨永磁体盘上相邻磁体的两个中心垂线，因此每对相邻磁体的一半N与S都会对等效磁体产生相应的斥力F1或F4和吸力F2或F3。Ft为永磁体对等效磁体两个方向作用力的切向合力，该切向合力所产生的转矩将驱动从动盘(铜盘及背铁)运动。

图4 等效磁体和初始永磁体的相互作用

2.2 解析模型理论计算

如图2所示，铜盘背铁层、铜盘层、空气层和永磁体盘层各区域均满足基本场域方程

B=μH+μ0Me

(1)

式中,B和H分别为磁感应强度和磁场强度，Me为永磁体的等效剩余磁化强度。μ和μ0为磁导率和真空磁导率。

B用矢量磁位A表示，并把式(1)两边同时取旋度有

(2)

由安培环路定律表述为

(3)

(4)

式中，φ为标量电势，υ为主动盘和从动盘的相对转速。

铜盘中的涡流电势是由主、从动盘相对运动过程中切割磁感线产生，因此只考虑铜盘中的动生电势对铜盘转矩的影响，不需要考虑感生电势，进而推导出矢量磁位A的变化率也为0。在二维层模型中，标量电势φ在z方向上不发生变化，其梯度也为0。因此，由式(4)得到

(5)

如图2所示，该涡流联轴器为对称结构，因此只需要写出一半结构所对应各区域的Laplace和Poisson方程

(6)

永磁涡流联轴器在工作过程中，其中的场量随着空间和时间变化，因此可将其在时谐场中进行分析，在前人研究的工作[9]基础上,建立针对本文涡流联轴器的永磁体区域等效剩余磁化强度Me的计算模型。由于本文模型的永磁体均为轴向充磁，故等效剩余磁化强度如图2所示只有y方向，并且随空间轴x与时间轴t周期性变化。文献[9]中指出，在利用傅里叶三角级数计算永磁体区域的磁化强度时，除基波以外的高次谐波对转矩的影响几乎可以忽略不计，故本文等效磁化强度只取一次基波，则有

(7)

式中，Br为永磁体剩余有效磁感应强度，m、p分别为单个磁极的平均周向长度和平均极距。s为相对转差率，ω1为电角速度，α1为一次基波的系数，其表达式分别为

(8)

(9)

(10)

由相量表示为

(11)

其中，

(12)

依据库伦规范，由式(3)、式(6)、式(11)可列出Laplace和Poisson方程有

(13)

式中，γ3和γ4分别为铜盘和铜盘背铁的电导率。

因此，经过分析计算得到二阶偏微分方程式(13)的解为

(14)

式(14)中,

(15)

式中，λ2与λ1的区别在于电导率的不同。

如图2各个区域所示，将解析解式(14)代入以下边界条件，得到8个线性方程，并利用Matlab求解出相应的系数。

(16)

式中，μeq为铜盘背铁的等效磁导率，μx为永磁体阵列区域在x方向等效磁导率并有

(17)

式中，μr为永磁体材料的相对磁导率。

2.3 铜盘的电磁转矩

铜盘电磁转矩是永磁涡流联轴器最主要的参数，基于能量守恒定律法的转矩表达式为

(18)

式中，P为铜盘转矩功率，Ω为主动永磁体盘和从动铜盘的相对角速度，Ω=Ω1-Ω2,Rav=(R4+R5)/2。

考虑到3D模型的端部效应，引入RUSSEL修正因子[10]并参考文献[3]中的参数公式有

(19)

其中，

因此，经过修正因子修正后的转矩表达式为

T′=KsT

(20)

3 有限元仿真

为了验证本文针对整体式双层永磁体双铜盘涡流联轴器所建立数学模型的正确性，利用软件Ansys Maxwell并结合表1的结构及材料参数建模仿真、网格划分，如图5所示。

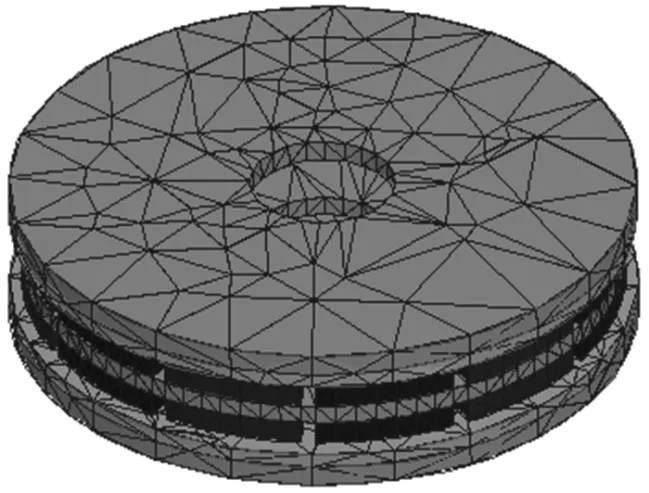
图5 有限元仿真模型及网格划分

表1 涡流联轴器主要参数

在空载条件下，保持表1中的参数不变，在相对转速n=30r/min、磁极对数p=6、铜盘厚度l2=6mm的动态条件下，对本文提出的永磁涡流联轴器进行动态仿真，由于运动过程中存在周期性，故只需取一对永磁体即1/6模型进行分析，从而得到如图6所示的仿真结果。在图6中，1处为N极、2处为S极、3处为位于1/2铜盘厚度处产生的涡流回路，涡流回路的圆心在相邻磁体气隙中心的竖直垂线上，且相邻涡流回路的旋向相反。从图6中可以看出，由于磁极极性相反的相邻磁极之间互相吸引形成聚磁效应，因而永磁体中心对应铜盘处产生的涡流密度J(单位：A/m2)较弱。

图6 铜盘厚度中心截面涡流密度分布

4 对比分析

4.1 等效磁导率的确定

根据表1的结构及材料参数，代入不同数值的铜盘背铁等效磁导率到前述模型的铜盘转矩解析式(20)中，计算出铜盘转矩的解析解。在相同条件下，进行仿真求解，所得结果如表2所示。需要注意的是本文设计的涡流联轴器为双铜盘结构，由于两个铜盘的转矩相同，故以下计算(图表分析数据)均只计单铜盘的转矩。

表2 不同铜盘背铁等效磁导率的铜盘转矩值

从表2中得出，在不饱和情况下，磁导率取50μ0和150μ0，铜盘背铁并未充分利用表面磁密强度，导致解析值明显小于有限元值。取500μ0甚至更大时，解析值将会随着铜盘背铁等效磁导率的增大几乎不再发生变化，且近似等于仿真值。因此，铜盘背铁等效磁导率的取值范围满足以下关系式

μeq≥500μ0

(21)

根据式(21)及表1计算得到，铜盘的解析转矩值和有限元仿真值的最大误差不超过3%，表明铜盘背铁等效磁导率的取值范围是在误差允许范围内的。本文的铜盘背铁等效磁导率取为μeq=2000μ0。

4.2 主要参数仿真对比

在永磁涡流联轴器的转矩计算过程中，影响较大的主要参数分别为磁极对数、铜盘厚度、相对转速、气隙长度、永磁体厚度等。在保持表2中参数不变的情况下，本文主要研究不同相对转速、不同磁极对数及不同铜盘厚度对转矩影响的变化规律。

图7为相对转速与铜盘转矩的关系。由图7可以看出随着转速的增加，转矩也相应增大，且转速越大解析解和仿真解的误差也逐渐增大，最大误差在n=80r/min处，约为11%，在误差允许范围内，验证了数学模型的有效性，也证明此数学模型适用于低速情况。

图7 磁极对数p=6、铜盘厚度l2=6mm的转矩速度特性

图8为磁极对数与铜盘转矩的关系。从图8可以看出，转矩对磁极对数的变化存在一个最大值即p≈6,T≈24N·m，数学模型较准确地预测转矩随磁极对数的变化，通过计算得出最大误差不超过7%。

图8 相对转速n=30r/min、铜盘厚度l2=6mm的转矩-磁极对数变化规律

图9为铜盘厚度与铜盘转矩的关系。从图9可以看出，转矩随铜盘厚度的增加，曲线的走向变化是先快后慢，l2=6mm时达到最大值，误差有先大后小再变大的趋势，这是由于铜盘的厚度与漏磁多少有关，厚度大漏磁较大，反之厚度小漏磁较少。因此，厚度在0～5mm时，仿真值大于解析值，大于6mm时，仿真值要小于解析值。在0～8mm的铜盘厚度范围内，数学模型的解析预测相对准确，平均误差约为4%。

图9 相对转速n=30r/min、磁极对数p=6的转矩-铜盘厚度变化规律

通过以上仿真对比分析，证明所建改进数学模型对该涡流联轴器具有预测意义。在相同条件下，将该新型涡流联轴器与文献[6]和文献[7]的涡流联轴器的转矩性能对比分析，相对于前者转矩性能显著提升，相比于后者，转矩性能几乎相当，但该新型结构独特的优势对多盘涡流联轴器的发展有促进作用。

5 结 论

本文针对所设计的整体式双层永磁体涡流联轴器，利用提出的等效磁体概念定性分析了铜盘转矩产生的机理；并利用二维层模型的矢量磁位法建立该结构的改进数学模型，进行解析求解；并对该结构形式的涡流联轴器进行三维有限元仿真分析，验证了数学模型，同时表明该涡流联轴器转矩性能良好。