无刷直流电机模糊自适应控制系统的研究
赵 红,赵德润,罗 鹏,2,郭 晨,张 军,王逸婷
(1.大连海事大学 船舶电气工程学院,辽宁 大连 116026;2.国网重庆市电力公司 万州供电分公司,重庆 万州 404001)
0 引 言
无刷直流电机(Brushless Direct Current Motor,BLDCM)是随着计算机科学技术、电力电子技术以及高性能永磁体材料的飞速发展而诞生的一款新型电机。其结构简单、体积小、重量轻、实用寿命长,同时还具有功率因数高、起动转矩大等优势[1],从而被广泛应用于新能源电动汽车、智能机器人、无人水面艇、高精度伺服电机等领域[2-5]。然而,现代工业水平的普遍提升以及智能制造行业的迅猛发展也无疑对传统BLDCM控制系统的控制性能提出了更高要求。为了进一步改善BLDCM控制效果,提高其控制性能,一些先进的智能控制算法如神经网络、遗传算法、模糊控制[6-7]等被逐步应用于BLDCM控制系统中。BDLCM本身具有多变量、非线性和强耦合等特点,而模糊控制恰好不需要对被控电机建立精确的数学模型且具有较强的鲁棒性,使其非常适合用于BLDCM的控制。例如文献[8-9]在Matlab/Simulink环境下已经对模糊PI控制算法在BLDCM控制系统中的应用展开了仿真研究并取得了良好控制效果,但没有进一步在工程实际环境中验证控制策略的有效性。文献[10]和文献[11]也分别设计了基于FPGA/DSP的BLDCM模糊调速系统,但DSP/FPGA具有芯片价格昂贵、控制电路复杂和电路板制作成本高等缺点,不宜在工程实际中普及应用。文献[12]以STM32为主控芯片,通过利用其性价比高、运行速度快等优势设计了BLDCM控制器,但因电机控制系统的速度调节器仍然采用传统PID控制算法,故其抗外界扰动性能不强、控制精度低。本文通过把模糊控制与PID控制有效结合并充分发挥彼此优势,设计了基于STM32的BLDCM模糊自适应PID控制系统来克服上述缺陷。最后经由上位机监控界面中显示的波形曲线易知,基于本文策略的BLDCM模糊自适应控制系统具有响应速度快、超调量小、鲁棒性强等特点。
1 无刷直流电机的数学模型
以BLDCM的二相导通星型三相六状态为例来研究其数学模型。由于BLDCM具有多变量、强耦合、非线性等特点,为了方便分析,首先做如下假定:
(1)三相定子绕组完全对称分布,定子电流亦对称。
(2)转子永磁体产生的气隙磁场为方波,转子磁场亦呈对称分布。
(3)忽略齿槽效应、电枢反应和换相过程等影响。
(4)磁路不饱和,不计磁滞和涡流损耗。
(5)忽略开关器件导通和关断时间的影响,导通压降恒定,关断后的等效电阻无穷大。
那么,其三相绕组电压平衡方程可表示为
(1)
式中,UA、UB、UC为三相定子绕组相电压,V;IA、IB、IC为三相定子绕组相电流,A;EA、EB、EC为三相定子绕组反电动势,V;Un为中性点电压;RS为三相定子绕组的相电阻,Ω;LAA、LBB、LCC为三相定子绕组的自感,H;LAB、LAC、LBA、LBC、LCA、LCB为三相定子绕组间的互感,H;q为微分算子且可表示为q=d(·)/dt。
因前述假定BLDCM三相定子绕组完全对称,且忽略了磁路间影响,那么可认为定子各相绕组间互感为常数,则有:
LAB=LAC=IBA=LBC=LCA=LCB=M
IAA=IBB=ICC=LS
由于三相对称星形绕组电机中存在IA+IB+IC=0,则有MIA+MIB+MIC=0,那么式(1)可整理为
(2)
根据式(2),可以得如图1所示的BLDCM等效电路图。
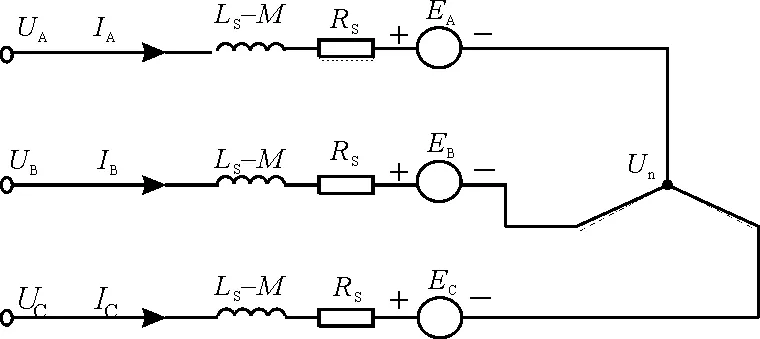
图1 BLDCM等效电路图
根据BLDCM运行特性,其电磁转矩和机械运动方程可分别表示为
(3)
(4)
式中,Te为电磁转矩,N·m;ω为电机机械角速度,rad/s;J为转动惯量,kg·m2;B为阻尼摩擦系数,N·m·s/rad;TL为负载转矩,N·m;dω/dt为转子机械角加速度,rad/m2。
2 BLDCM模糊自适应控制系统的整体仿真模型搭建及其运行结果分析
在Matlab2014a版本的Simulink环境下充分利用Simpower System工具箱提供的丰富模块库并结合S函数,搭建了基于模糊自适应PID的BLDCM控制系统整体仿真模型,由具有独立功能的各个子模块组成,且该控制系统采用电流、转速双闭环的控制策略,其整体仿真模型如图2所示。
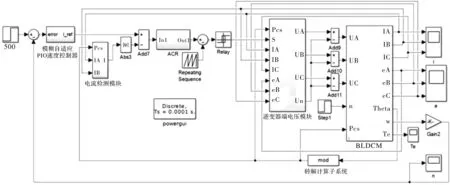
图2 BLDCM模糊自适应控制系统整体仿真模型
2.1 无刷直流电机本体模块
BLDCM本体模块在整个仿真控制系统中起着至关重要的作用,搭建过程主要依据上述电压平衡方程、电磁转矩方程以及机械运动方程等来完成。其仿真模块如图3所示。该BLDCM本体仿真模块主要包括相电流输出、转矩转速计算以及梯形波反电动势的获取等环节组成。
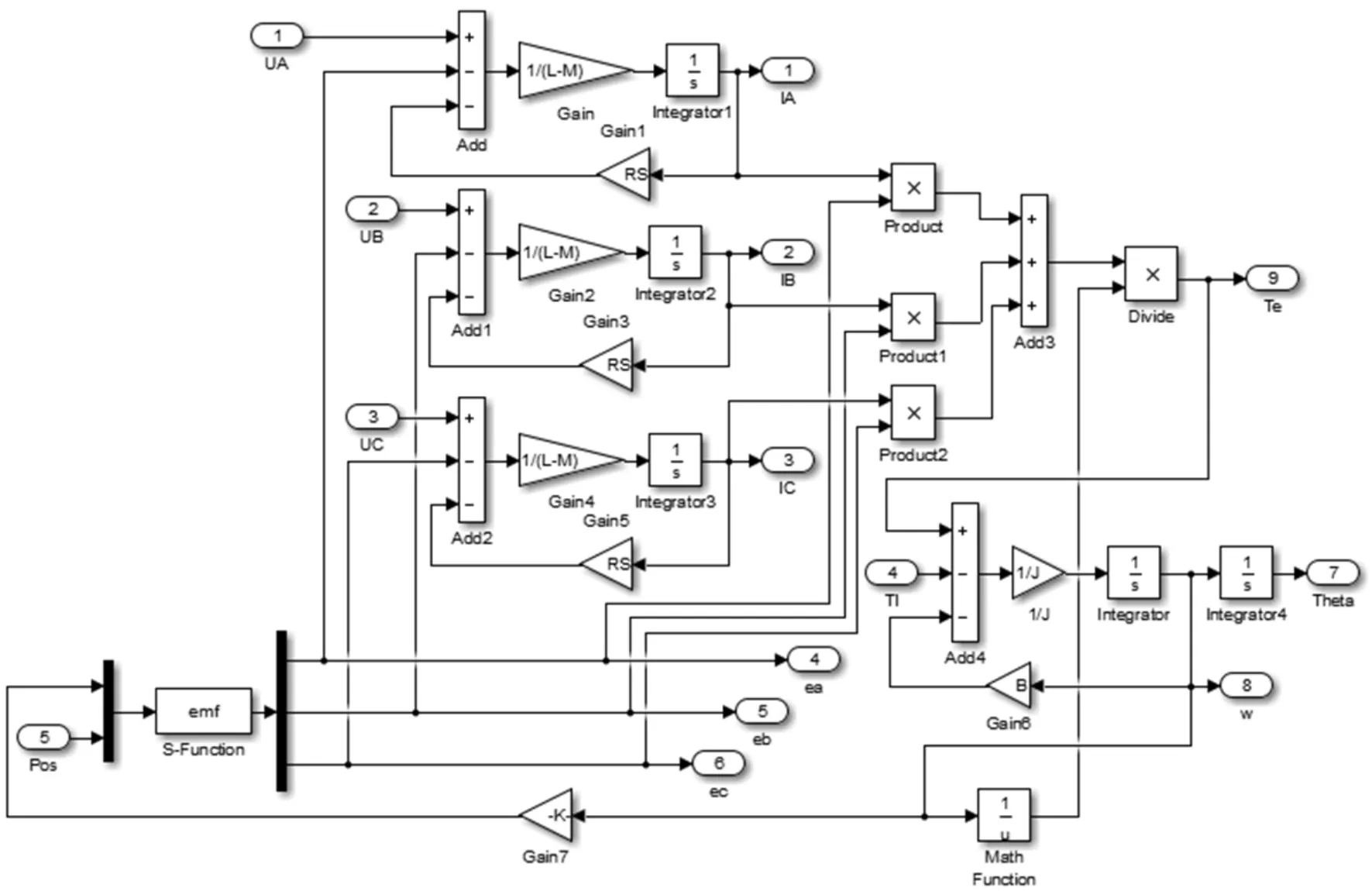
图3 BLDCM本体仿真模块
其中,反电动势波形的获取会直接影响并决定着电机本体仿真模块的性能。目前获取反电势的常用方法有:有限元法[13]、傅里叶变换法[14]以及分段线性法[15]。由于分段线性法简单易行且精度较高,能更好地满足电机本体模块的仿真要求,故本文选择了分段线性法。运行在二相导通星型三相六状态下的BLDCM梯形波反电动势波形如图4所示。同时,转子位置和与反电势之间的线性关系可由表1来诠释,其整个过程由S函数编程实现。
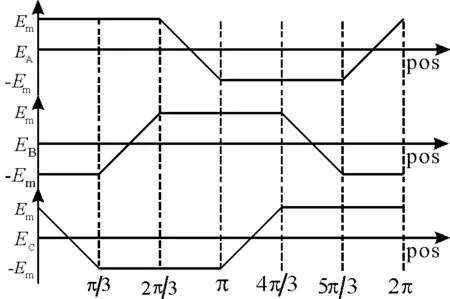
图4 三相梯形波反电动势波形
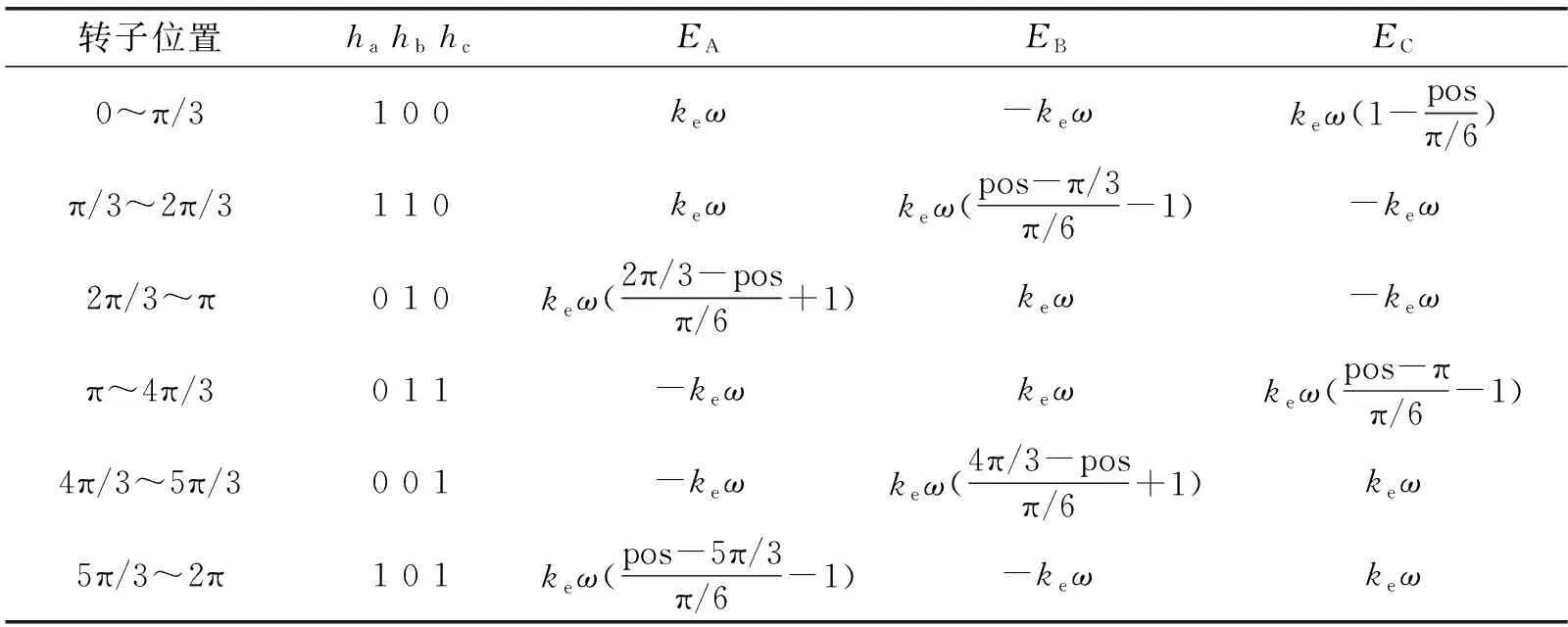
表1 转子位置和反电动势之间的线性关系表
2.2 逆变器端电压及中性点电压获取模块
当电机工作状态处于换相三相导通模态时,端电压方程可表示为
(5)
(6)
(7)
式中,S代表PWM信号,导通时,S为1,关闭时,S为0,Ud为直流母线电压。三相对称星形绕组中始终有IA+IB+IC=0存在,根据式(5)~式(7)可知中性点电压为
(8)
当电机运行状态处于换相结束两相导通模态时,其端电压方程为
(9)
(10)
UC=EC+Un
(11)
此时,有IC=0存在。由式(9)~式(11)易知中性点电压:
(12)
如式(8)和式(12)所示,中性点电压在换相续流和换相结束两个阶段呈现不同的值,但都可通过三相反电动势、转子位置角θ以及三相定子电流表示,其转子位置和中性点电压之间的对应关系如表2所示。

表2 转子位置与中性点电压对应关系表
鉴于SimpowerSystem中的通用逆变模块算法固定且计算效率低,无法呈现上述过程,故本文采用S函数实现此功能,其逆变器端电压及中性点电压整体仿真模块结构如图5所示。
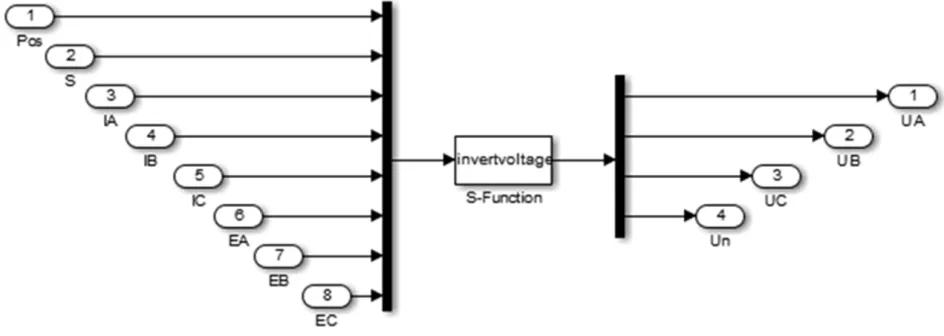
图5 逆变器端电压及中性点电压获取模块
2.3 电流调节及PWM信号产生模块
BLDCM的三相电流流通情况可通过检测转子位置角θ来进行判断。如图4所示,当0≤θ﹤π/3时或者π≤θ﹤4π/3时,B相为非换相相,此时可以检测B相电流绝对值作为电流内环反馈。以此类推,总结了如表3所示的反馈电流信号的检测规律。
此表中的电流信号反馈检测规律也是由S函数实现的。如图6所示,电流调节器ACR采用三角波作为载波来进行比较控制,将参考电流iref与电流反馈检测值ifeed之差经比例积分环节进行处理,其输出信号值ui与三角载波ur之差再经滞环比较器处理,从而输出相对应的PWM信号来对电机的逆变器进行驱动。

表3 反馈电流信号的检测规律
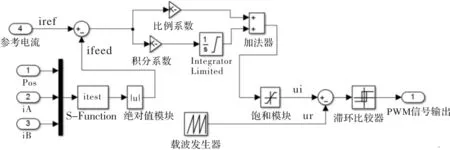
图6 电流调节及PWM信号产生模块
2.4 模糊自适应PID速度控制器模块
模糊自适应PID控制器充分利用模糊推理来使得PID控制器参数能够根据误差和误差的动态变化率实时调整,进一步提高电机控制系统的自适应能
力,从而获得最佳的转速响应变化曲线。BLDCM的模糊自适应PID控制结构框图如图7所示。

图7 BLDCM的模糊自适应PID控制器结构原理图

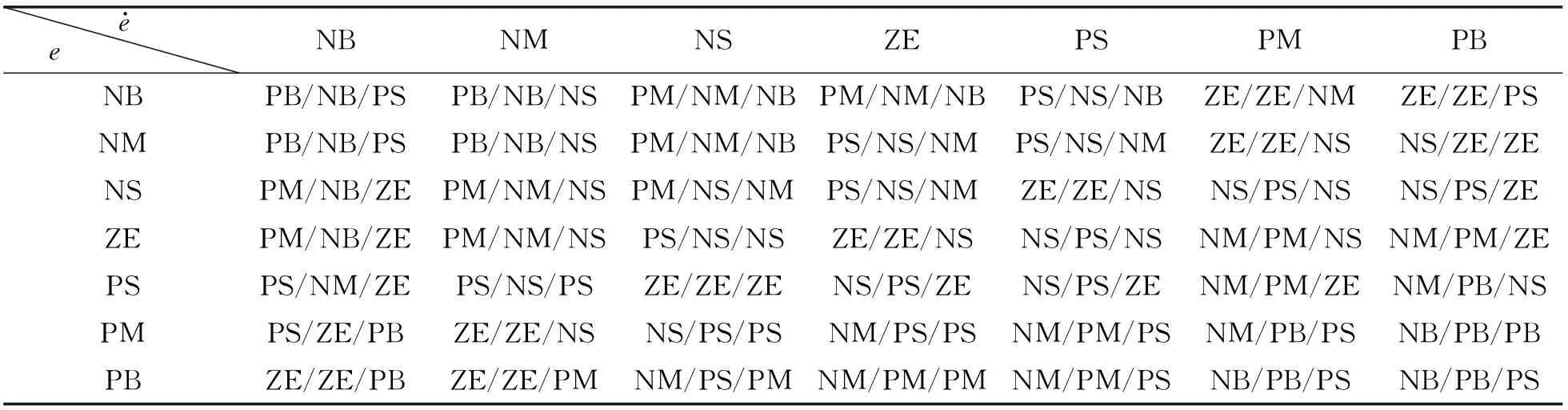
表4 ΔKp、ΔKi、ΔKd的模糊控制规则表
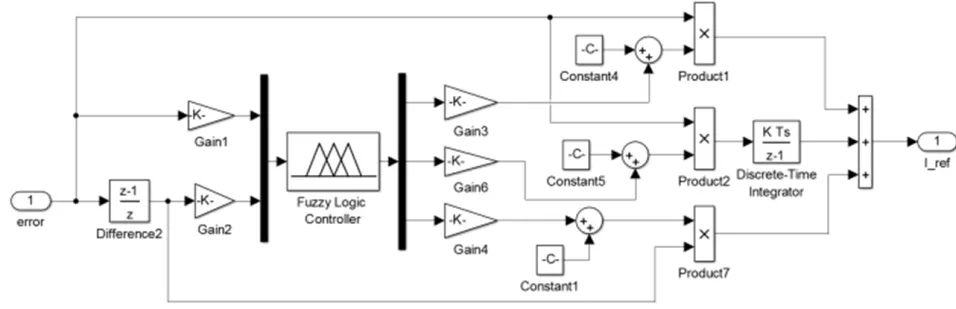
图8 模糊自适应PID速度控制器仿真模块
2.5 仿真运行结果与分析
在仿真实验中,BLDCM采用型号为57BL55S06-230TF0的电机,其参数为RS=1.15Ω,LS=0.0021H,M=0.061H,J=0.001kg·m2,转子极对数为2,B=0.0002N.m.s。依据上述电机参数,在额定负载转矩下,分别基于传统PID控制及本文模糊自适应PID控制策略下运行图2所示的BLDCM整体仿真模型,得到不同转速给定下的转速响应变化曲线,如图9和图10所示。

图9 PID控制方式下的转速动态响应变化曲线
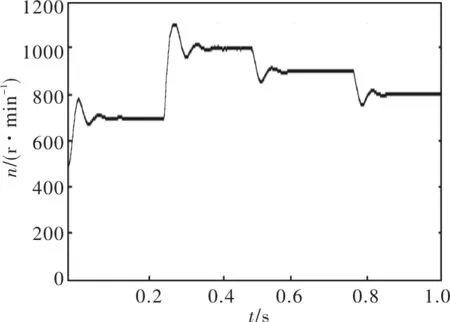
图10 模糊自适应PID控制方式下的转速动态响应变化曲线
其中,图9为基于传统PID控制的仿真结果,图10为基于本文控制策略的仿真结果。对比显见,基于本文控制策略的转速动态性能更优越。
3 实验平台的搭建与实验结果分析
为进一步验证本文策略的有效性,以STM32F103RBT6为核心处理器搭建了基于模糊自适应的BLDCM控制系统实验平台,如图11所示。其中,实验过程中所使用电机的参数如下:额定转速为3000r/min,额定电压为24V,额定电流为3.3A,额定转矩为0.18Nm。
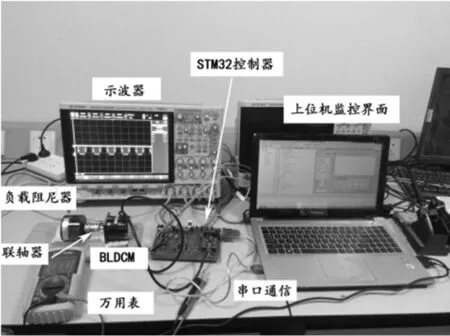
图11 BLDCM控制系统实验平台
为了便于展示实验结果,还设计了基于Matlab/Gui 的上位机监控界面来实时显示转速的动态变化情况。STM32下位机与Matlab之间则通过串口通信来完成转速等其它数据信息的实时传送,从而可以在GUI界面中实时得到转速动态响应波形变化曲线。BLDCM控制系统实验平台的上位机监控界面如图12所示。

图12 BLDCM上位机监控界面
最后以负载阻尼器作为负载,分别采用传统PID控制和模糊自适应PID两种不同控制算法进行了转速实验的对比研究。图13为电机在起动过程中的转速变化响应曲线图,对比可见:采用基于本文的模糊自适应PID控制算法时,电机在起动时具有超调量小的优点,且在正常运行过程中转速波动较小,更加平滑。图14为电机在转速为1000r/min的平稳运行状态时,转速给定突然上升为1300r/min的转速变化响应曲线。对比可见:BLDCM在采用基于本文模糊自适应控制算法时具有更快的响应速度,能够使得电机转速更迅速平稳地跟上给定转速,且抗外界变化能力较强。
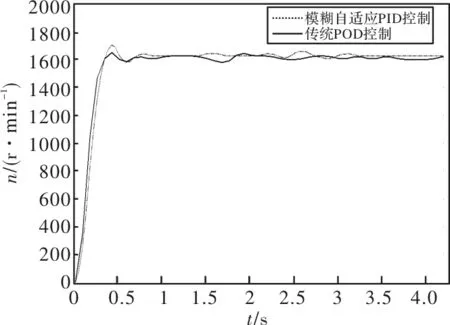
图13 BLDCM起动过程中的转速动态响应曲线
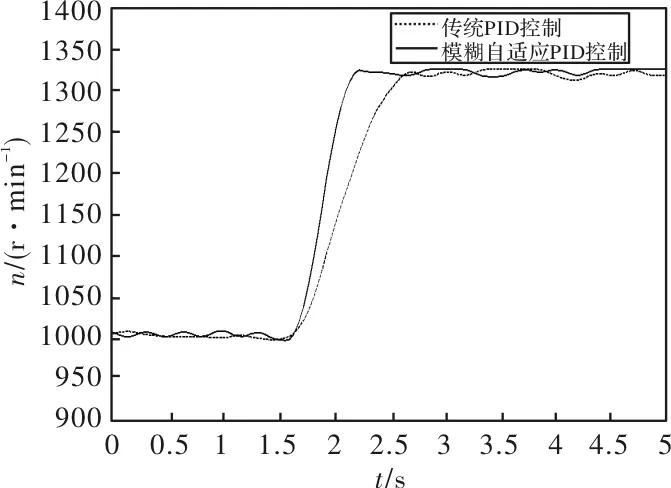
图14 BLDCM在转速给定突变时的转速动态响应曲线
4 结 论
针对传统BLDCM控制系统时常伴随着动态响应速度慢、抗外界扰动变化能力差、鲁棒性不强等困扰,本文提出了在BLDCM控制系统应用模糊自适应PID控制算法来克服上述问题。最后,通过分别建立BLDCM控制系统仿真模型和搭建基于STM32的BLDCM控制系统实验平台验证了本文所提出控制策略的正确性和有效性。

