电子式互感器数字积分器技术的研究

饶超平

（武汉晴川学院，湖北 武汉430000）

0 引 言

电力线路的测量要采用高精度数字积分器。因此，高精度积分器的设计是减小复合误差的关键。本文通过理论分析和仿真实验，对理想积分算法和梯形积分算法进行了对比，寻找适合的理想积分算法。

1 理想模拟积分器

模拟积分器分为有源和无源两种。无源积分器由于对信号的幅度有衰减，输出阻抗较大，在测量要求精度高的场合，特别是工频小电流时会带来很大误差。因此对于工频电流测量，常用有源积分器予以设计实现。实际应用中，需要抑制积分器的“积分漂移”。如图1所示，为了保证积分器能够长期稳定地工作，可在积分电容C1的两端并联一个反馈电阻R2，为积分漂移电压提供反馈通道。图1为典型有源负反馈模拟积分器，其传输函数为：

理想模拟积分器与有源负反馈模拟积分器相比，区别在于不含图1内的负反馈电阻R2，其传输函数为：

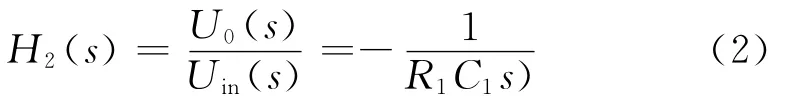
理想模拟积分器中使用的运算放大器只有在线性工作区内可以正常工作，存在饱和问题。因此在实际使用中，在放大器的积分电容C1两端并联反馈电阻R2，用以消除放大器的饱和。但是若积分器的反馈参数配置不当，其暂态输出波形将严重失真。适当地提高积分器的反馈电阻值以及积分电容值可以改善其暂态传变特性。以上两种积分器共性的缺点为：频率很小时，增益很大，因此信号中直流分量的影响较大。

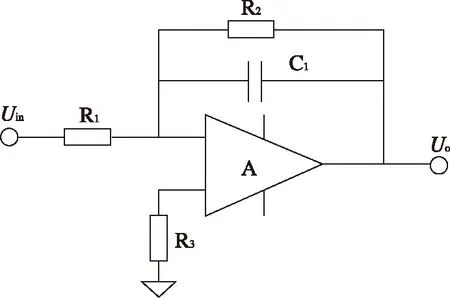
图1 典型有源模拟积分器

2 积分环节的原理及其性能对比

积分器在测量与控制工程中使用极多，是信号处理环节的核心之一。对于电流互感器，其核心环节在于将二次侧输出信号还原为与一次电流、电压信号成比例的信号，常见方案有模拟积分器和梯形积分器。下面将对其性能与效果做具体对比并分析。梯形数字积分算法在实际应用中，由电子式电流互感器按一定个数的工频周期（即设定的积分常数时间）采样一定点数，按照如下公式进行计算：

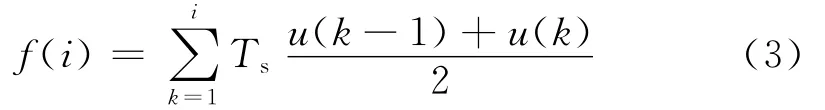
式中，u（k）为二次侧的变换输出量；Ts是采样周期；f（i）为经过计算的输出量。该公式经过傅里叶变换可以转换到时域进行对比：

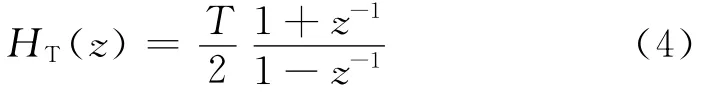
按照公式（4）进行转换为数字角频率，绘制出梯形传递函数的幅频特性与相频特性，可以得出幅值响应和相位响应的比较如图2。由图2可以看出，在数字角频率趋于无穷小时，幅值响应绝对误差最小，而在整个频带上，梯形算法与理想积分相位响应基本一致（图中实线为数字角频率，虚线为模拟角频率。）

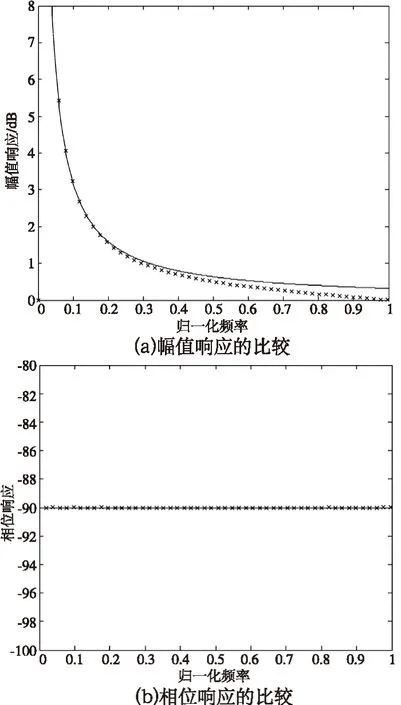
图2 梯形积分与理想积分

3 结束语

对于测量电力系统的电流互感器来说，其数字积分器具有以下特点：性能稳定，采用软件算法作为基本支撑，不容易受到外界温度的干扰。数字积分器可采用模数转换器结合微处理器的方法制作，架构简单。其中，梯形算法与理想积分相位响应基本一致，幅值响应绝对误差最小。所以，理想的数字积分算法有利于提高电子式电流互感器的测量精度。