基于绕组变匝数的永磁同步电机拓宽调速范围理论研究

张润波,林荣文,高靖凯

(福州大学,福州 350108)

0 引 言

近年来，随着永磁材料的发展以及能源危机的出现，越来越多的汽车厂商将永磁同步电机应用到汽车驱动系统中。衡量汽车性能的重要指标包括控制系统占用空间大小、驱动系统低速转矩性能、调速范围的大小。现今大多数研究都是通过改进永磁同步电机的控制方法或者重新设计电机本体来提高控制性能，但是这会带来控制算法复杂，稳定性差和费用较高的问题，所以寻求一种控制算法简单、效率高、成本相对较低的方法来控制电机，使其尽量满足上述方面的性能要求一直是学者研究的重点。

本文在已有电机定子绕组变匝数拓宽电机调速范围的理论思路下，先通过在MATLAB/Simulink中仿真验证该方法的有效性，然后通过具体实验来验证该理论,使电机在低速具有大转矩,电机转速范围大幅拓宽，而且控制方法简单有效，电机绕组加工简单，系统整体变动不大，具有较大实用价值。

1 交流电机变绕组匝数方法

交流电机在额定转速以下恒转矩运行，该区间能保证电机低速具有大转矩。当需要运行在额定转速以上时，可以对电机进行变极调速，即通过改变电机绕组接法来改变电机的极对数。在低速时极对数较多，需要高速运行时使极对数减少[1-2]。虽然该方法能达到要求，但是所用器件较多，占用空间较大，系统成本较高，不满足经济要求。对于永磁同步电机可以进行弱磁控制[3]，永磁同步电机的弱磁能力受永磁体强度和逆变器电压、电流的限制，在电动汽车中，整个驱动系统的体积受到限制，导致逆变器的电压等级有限，所以弱磁控制升速的范围也受到限制。

本文通过改变电机接入控制系统的绕组匝数来改变电机运行时的反电动势，进而拓宽电机调速范围[4-6]，控制系统框图如图1所示。此种方法对电机本体改动不大，需要电机定子绕组有中间抽头，当电机运行在额定转速以下时，控制电机全部绕组接入系统；当电机运行在额定转速以上时，控制部分绕组接入系统。

图1 绕组变匝数控制系统图

2 交流电机变匝数调速理论

三相表贴式永磁同步电机在d-q坐标系下的电压方程如下：

(1)

磁链方程：

(2)

反电动势方程：

ECEMF=ωeψds∝Ns

(3)

转矩方程：

Te=1.5pψdsiq

(4)

式中：Ud,Uq为定子电压的d,q轴分量；id,iq为定子电流的d,q轴分量；R为定子绕组电阻；Ld,Lq为定子绕组d,q轴电感；ψd,ψq为定子磁链的d,q轴分量；ψf为永磁体产生的永磁磁链。

由式(1)～式(4)可知，当电机运行在额定转速以下时，电机的反电动势随着转速的升高而增大。当到达额定转速时电机的端电压已经接近逆变器的供电电压，继续升速可以增加逆变器电压等级，但是这种做法只能增加逆变器的体积和整个系统的成本。而用绕组变匝数的方法在额定转速以上时只需开通控制部分绕组的开关管SW1，使部分绕组继续投入运行，而另一部分绕组通过对电容充电来释放能量。

电机定子绕组匝数减少一定比例之后，电机定子侧耦合的磁链相应地减少一定比例；同样，在相同转速时反电动势也相应地减小相同比例。这样，反电动势就会有进一步增加的空间，电机也就能在基速以上运行。基于变绕组匝数理论的电机转矩、电压、功率与转速的关系，如图2所示。

图2 绕组变匝数转矩、电压、功率与速度关系

电机绕组匝数的减少首先改变了电阻、电感以及磁链参数；其次在电机电压电流极限值不变时，不仅改变了转矩，而且转折速度也发生了改变。

不计电阻时，电机的电磁转矩以及转折速度可表示为下式：

Tem=p{ψfilimsin(β1+90°)+

(5)

(6)

式中：β为电机定子电流角;ρ为电机凸极率;ξ为弱磁率。

(7)

可知，在其他参数不变的情况下，定子的电抗与每相绕组匝数的平方成正比。以切换一半绕组为例，当电机需要运行在额定转速以上时，控制SW1开通，SW2关断，电机绕组电感、电阻以及定子侧耦合的磁链变化如下：

(8)

式中：下标1代表全部绕组，2代表部分绕组。

将式(8)代入式(4),式(5)得到：

(9)

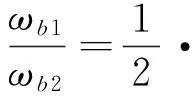
(10)

对于表贴式永磁同步电机,Ld=Lq, 则切换后电磁转矩变为原来的一半，转折速度为原来的2倍。因此当电机在低速时，使用全部绕组可以产生大转矩；当需要运行在额定转速以上时，通过减少一定比例的绕组匝数，进而减小反电动势，从而扩大了转速范围。

3 仿真验证

为了验证绕组变匝数拓宽永磁同步电机调速范围理论的正确性，首先在MATLAB/Simulink中搭建控制系统的仿真模型。在Simulink系统中电机模型都是固定的，运行过程中不能改变电机模型的电阻、电感、永磁磁链等参数，而用2个电机设置2种参数组合搭建的模型容易使电流和转速不连续，与现实运行情况差别较大，对最终验证该理论的正确性带来较大影响。而系统中自带的S函数则能较好地解决这个问题，通过设置电机的速度为临界点来改变接入系统的绕组参数。该方法简单可靠，更加直观的验证了结论。

仿真电机的原始参数如表1所示。

基于以上参数搭建的永磁同步电机的S函数仿真模型如图3所示。

图3 基于S函数的永磁同步电机模型

控制方法采用传统的id=0的矢量控制，以速度环作为外环，电流环作为内环的双闭环控制系统，如图4所示。它主要包括定子电流采样、速度检测、转子位置计算、Clarke变换及逆变换、2个Park变换及逆变换、速度环PI调节器、电流环PI调节器和SVPWM等环节。

图4 控制系统矢量框图

当电机空载运行时，测量其在不同绕组匝数时所能达到的最大转速，如图5所示。在全部绕组接入时，电机能达到的最大转速为1 800r/min，而当一半绕组接入时，电机所能达到的最大转速大约为3 600r/min。

图5 电机在不同绕组匝数的最大转速

图6为电机在不同绕组匝数时加速运行到2 000r/min时的电磁转矩波形。

图6 不同绕组匝数时的电磁转矩图

仿真中电机额定转速1 500r/min，将绕组切换转速设置为电机额定转速，电机给定转速为2 000r/min。由图6可以看出，电机在转速为1 500r/min以上时，电机切换为一半绕组运行，此时电机转速在1 500r/min到2 000r/min时的最大电磁转矩约为1 500r/min以下时的最大电磁转矩的一半，证明了式(9)的正确性。

图7为电机在相同负载转矩时的电流变化图。转速及负载转矩不变，在0.5s时刻接入部分绕组，部分绕组匝数稳定运行时的定子电流大约为全部绕组匝数稳定运行时的电流的2倍。

图7 切换时电流变化

图5～图7可以验证绕组变匝数理论适用于拓宽永磁同步电机调速范围。当永磁同步电机在额定转速以下时，使用全部绕组，此时能产生大转矩；当在额定转速以上运行时，需要减少一部分绕组匝数，此时电机额定转矩会相应减少，调速范围的大小以及电磁转矩的变化程度取决于减少的绕组匝数。

4 实验验证

为了验证该理论对于拓宽永磁同步电机调速范围的有效性，搭建基于DSP2812为控制核心的实验平台，实验平台如图8所示。

图8 实验平台

4.1 电机参数及测量

由于电机绕组的匝数与每相绕组匝数成正比，所以只需将原来每相绕组匝数减少相同比例，电机总绕组匝数就相应地减少相同比例。本文所用实验永磁同步电机原型机型号为YT-75-4，参数如表2所示。

表2 实验电机参数

考虑实际情况，本文将电机绕组总匝数拆分为70匝和35匝。当电机需要运行在额定转速以上时，电机绕组匝数减少35匝，电流不至于增加太大。这样，当电机匝数为70匝时，额定转速扩大：

经过加工后的电机如图9所示。

图9 加工后的永磁同步电机

由感应电机拖动永磁同步电机，测出其在不同转速下的相反电动势幅值，可以得到该电机的永磁磁链，数据如表3所示。

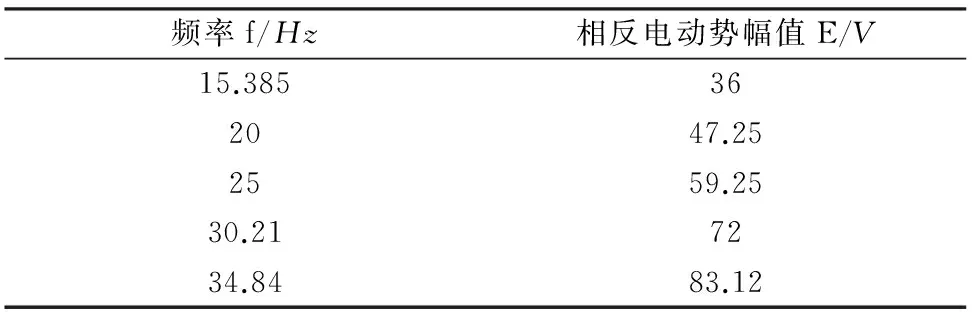
表3 相反电动势与频率

反电动势曲线如图10所示。

图10 频率与相反电动势幅值关系图

由图10可以看出，相反电动势与频率成正比，即可得出永磁磁链的值。

4.2 实验结果分析

4.2.1 转速、转矩稳态波形

图11为电机在全部绕组匝数，额定转矩，速度分别为900r/min，1 200r/min，1 500r/min稳定运行时的转速、转矩波形。采用id=0的控制方法时，电机的转矩与iq成正比，实验波形通过CCS软件截取，反映电机实际运行时的转速以及电流变化情况。电机实际速度以及转矩都能直观地在转速转矩测量仪上显示。

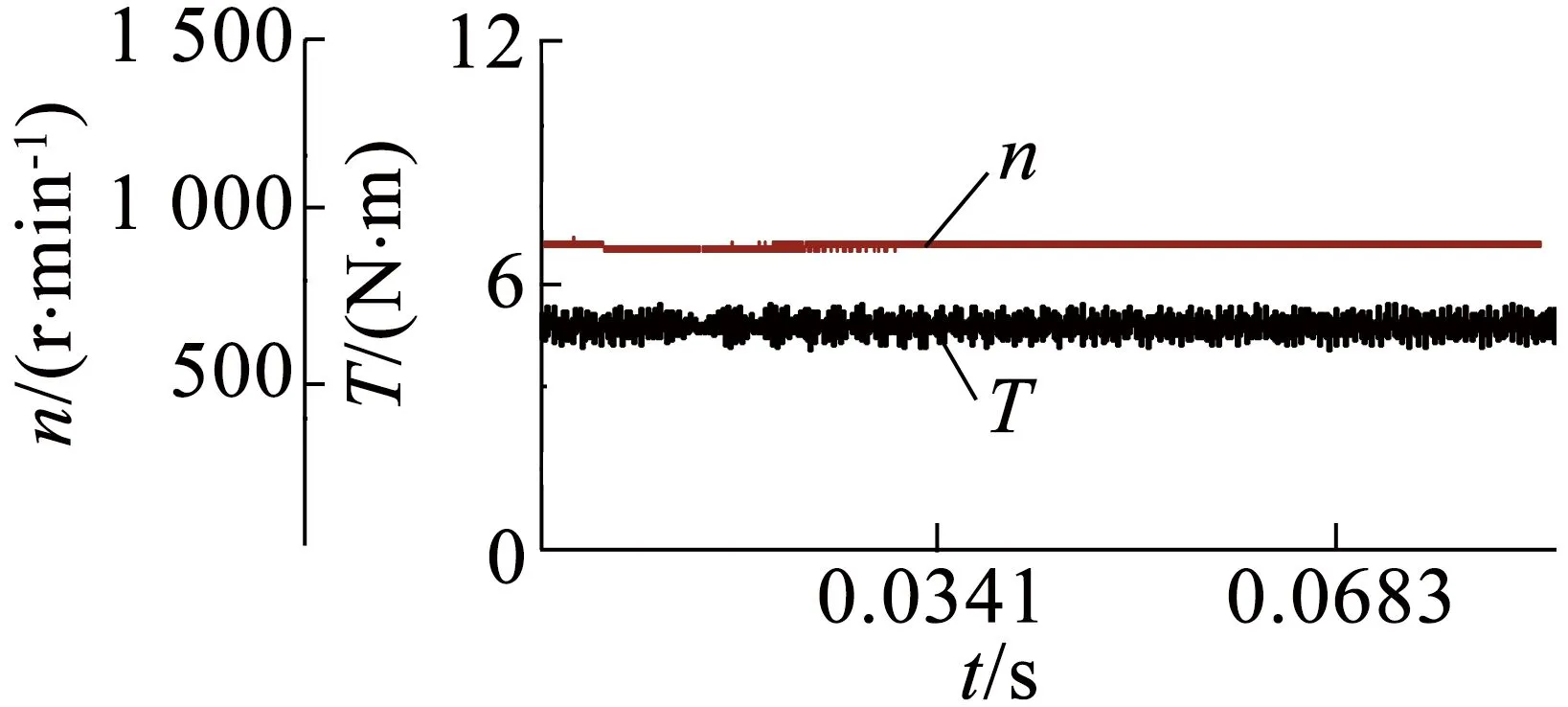
(a) n=900 r/min

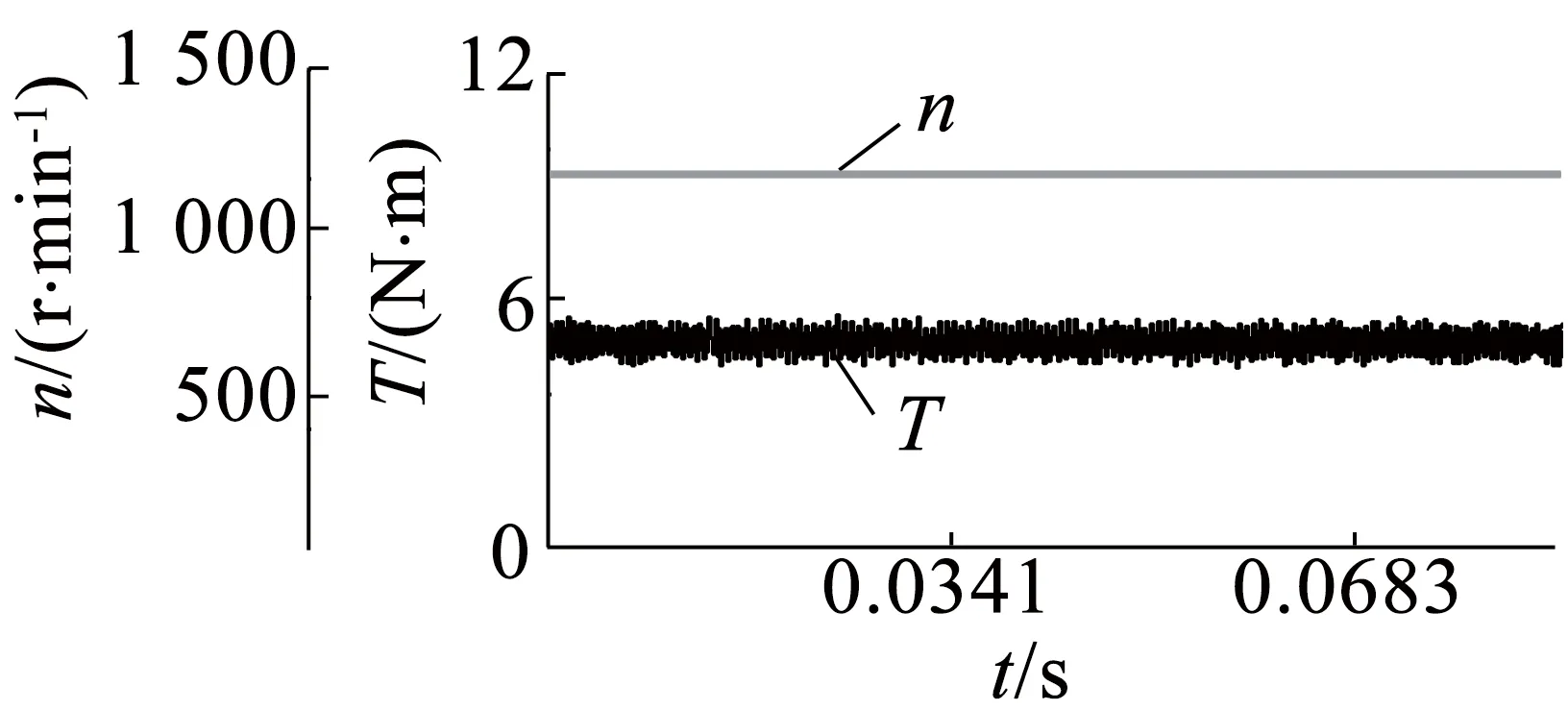
(b) n=1 200 r/min

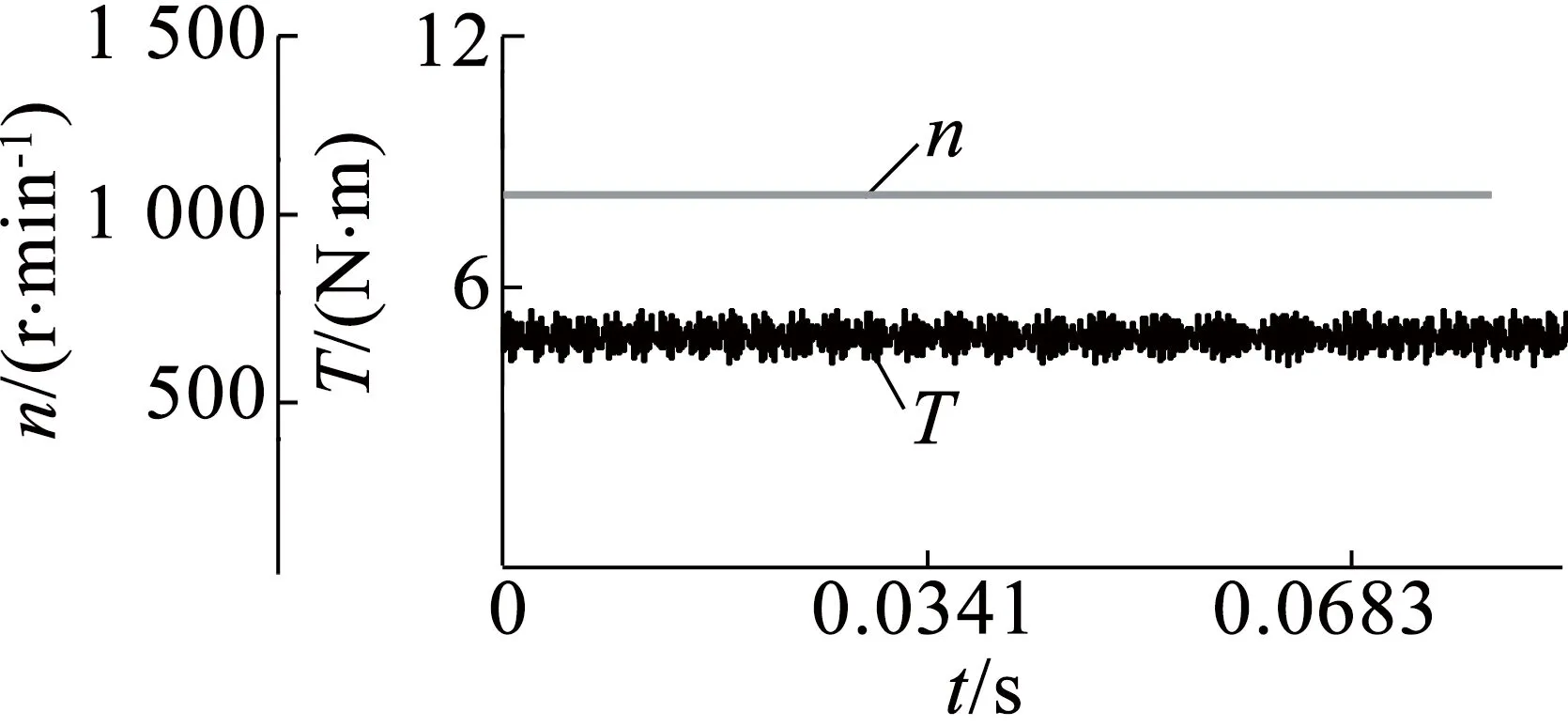
(c) n=1 500 r/min

由图11可以看出，电机在额定转速以下运行时，与普通未经过绕组加工的永磁同步电机具有相同的转速与转矩输出特性，转速与转矩控制性能完全不受影响，而且转速误差小，转矩脉动小。

图12则是电机运行在部分绕组匝数时，速度分别为1 800r/min,2 100r/min，带额定转矩时的波形。

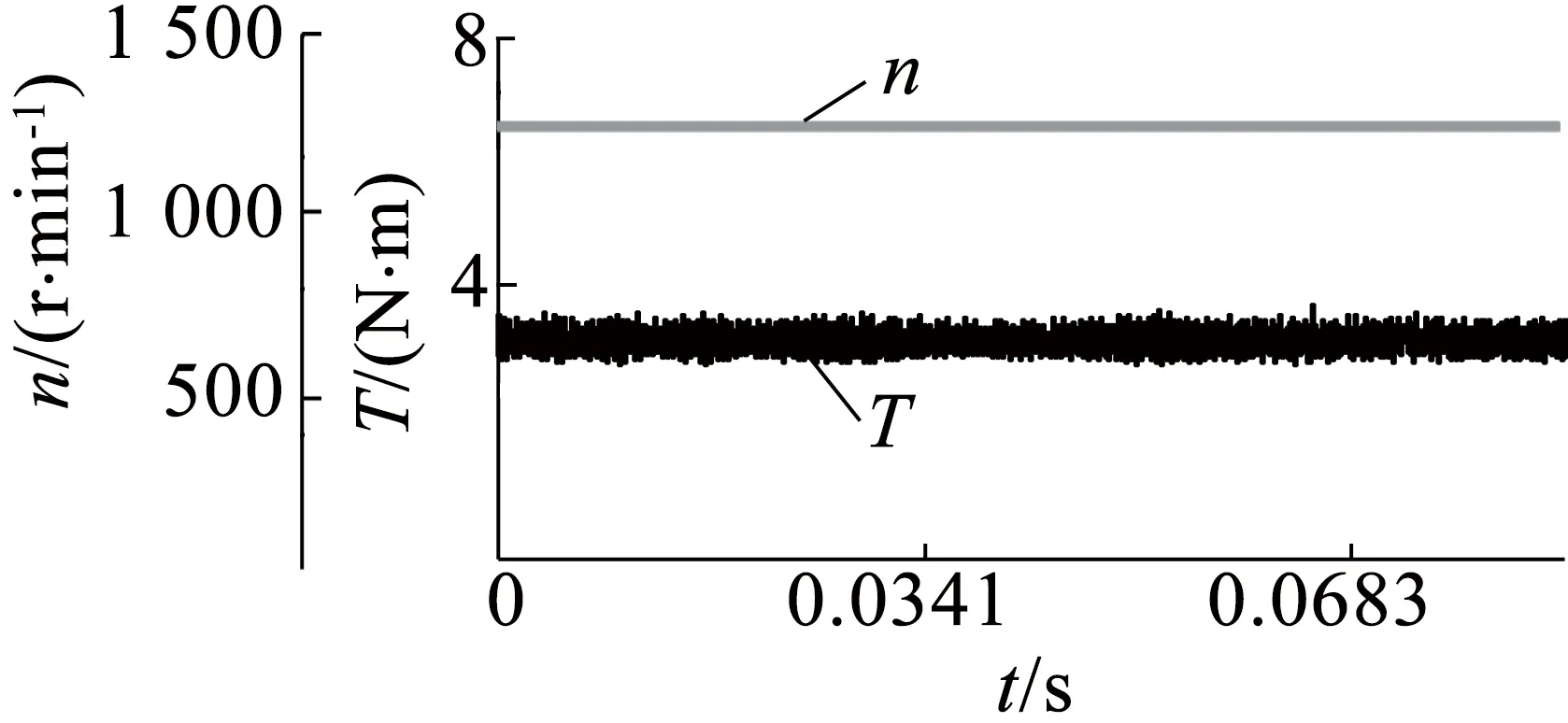
(a) n=1 800 r/min

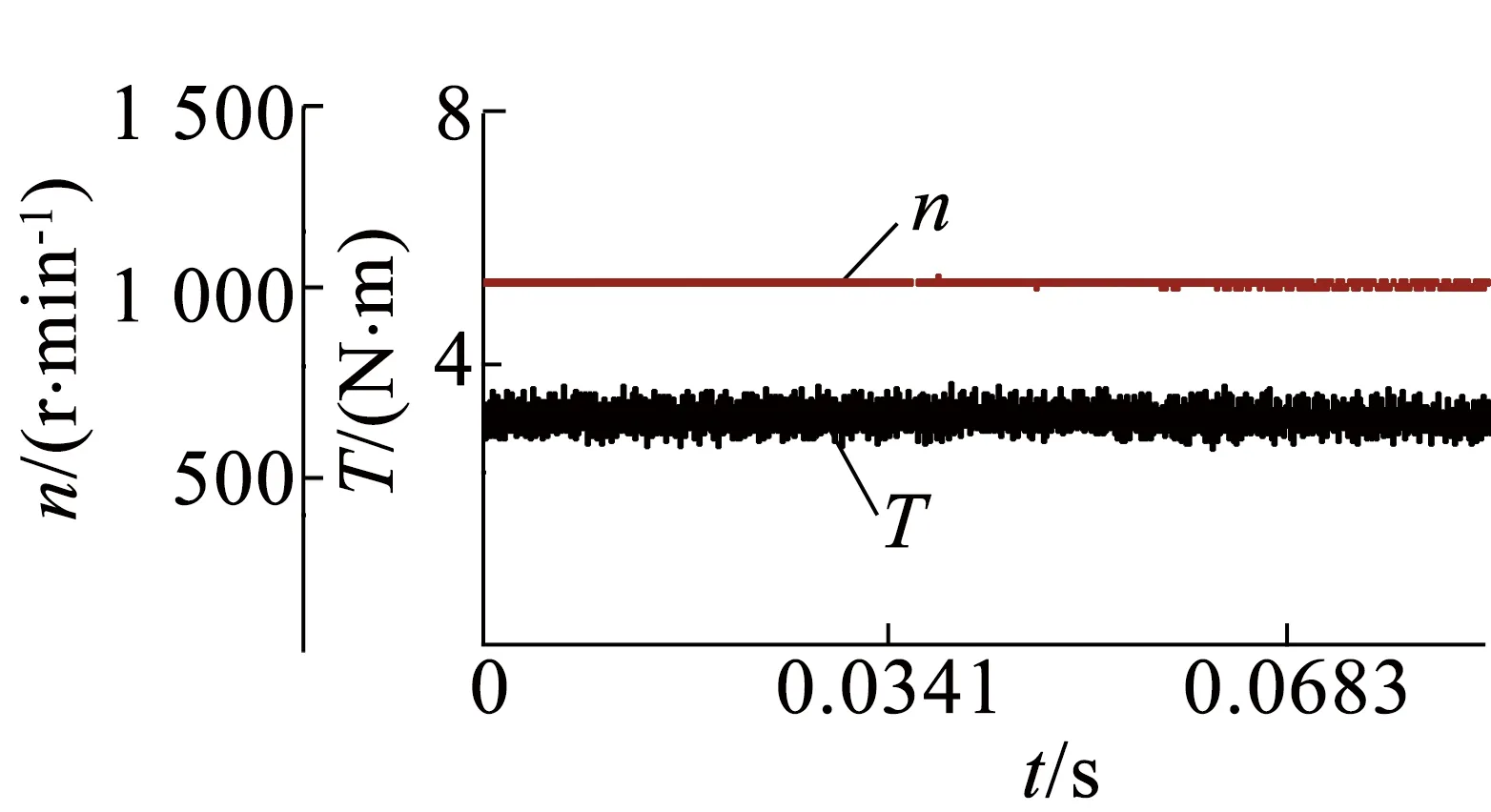
(b) n=2 100 r/min

电机在部分绕组匝数运行时速度达到2100r/min,而且随着转速上升到2 250r/min之前，额定转矩不变,即切换后可视作一台其他参数不变，额定转速上升到2 250r/min，额定转矩变为3.18N·m的永磁同步电机在稳定运行。

4.2.2 绕组切换瞬态波形

图13～图15为电机在空载条件下切换瞬态电流波形。设定电机速度1 500r/min为临界点发生切换，速度由1 485r/min上升到1 515r/min以及由1 515r/min下降到1 485r/min。

由图13～图15可以看出，电机在空载绕组切换之后，电流会相应变化。当匝数减少时，线电流增加；匝数增加时，线电流减小，而且用IGBT进行切换，总体切换时间较少，中间过程过渡平稳。

图13 空载升速切换

图14 空载降速切换电流

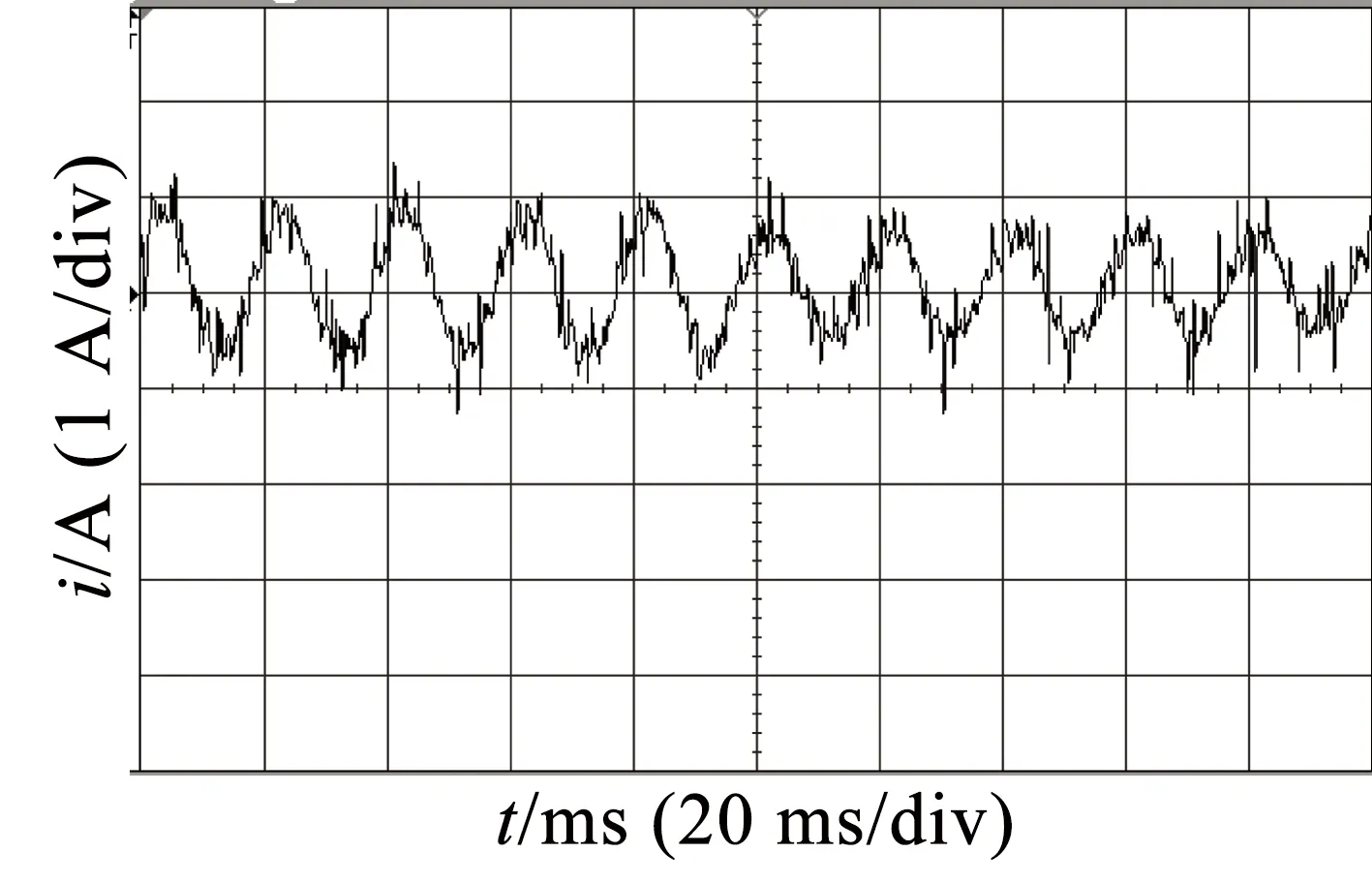
图15 降速过程电流放大

图16～图18为电机在转矩为3.18N·m时切换波形图，速度由1 485r/min上升到1 515r/min以及速度由1 515r/min下降到1 485r/min。

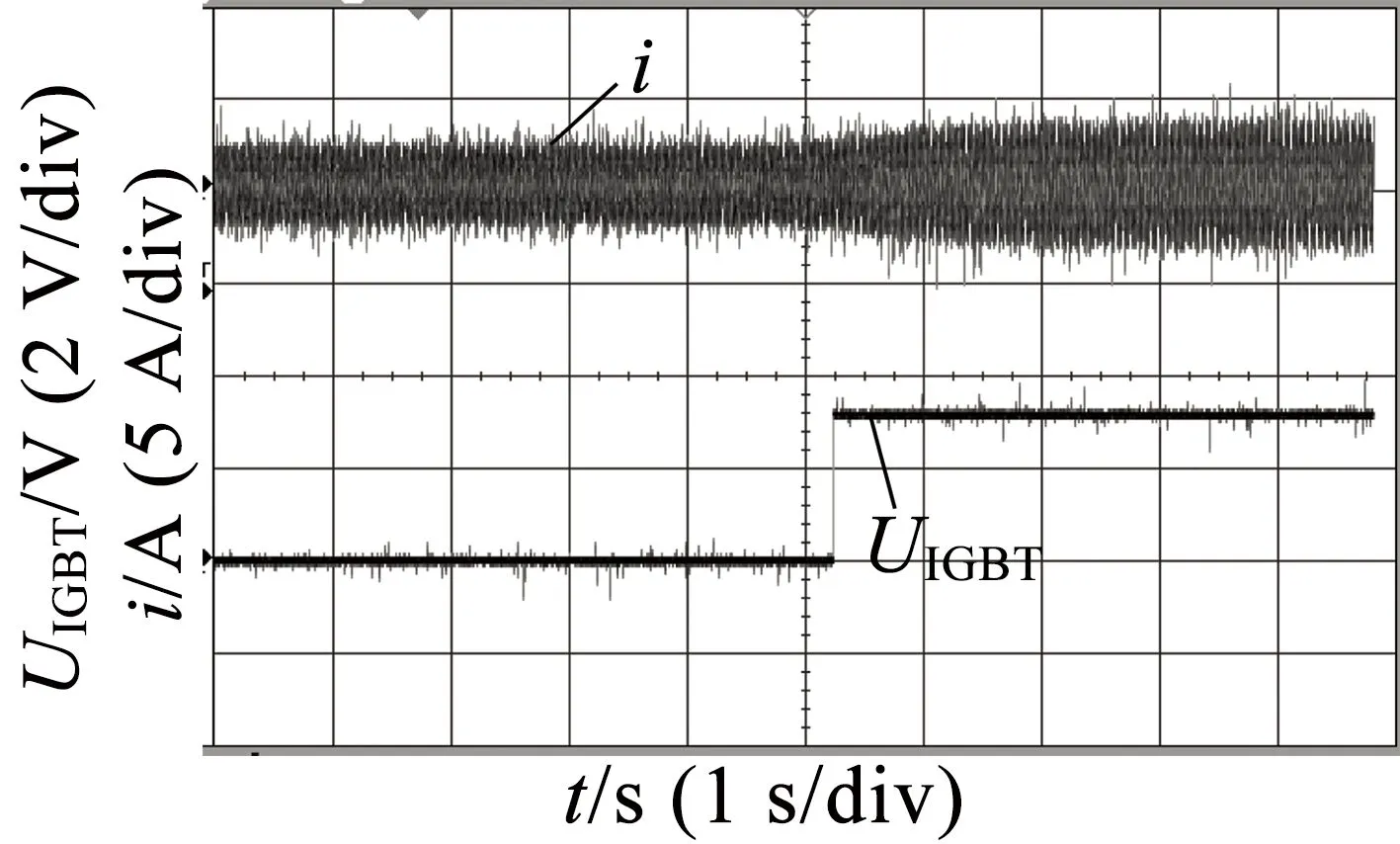
图16 满载升速切换

图17 满载降速切换

图18 升速过渡过程电流放大

由图16～图18可以看出，在切换时间内，电流变化缓慢，则对应电磁转矩变化缓慢，中间过程较为平稳。如果要精确确定过渡过程，则需要根据实际电机参数以及运行情况来确定切换时间。从上述稳态以及瞬态实验结果可以看出，绕组变匝数理论能有效提升永磁同步电机的速度范围，而且利用IGBT切换绕组具有响应时间短，驱动体积小，无噪声的特点。

5 结 语

本文将绕组变匝数拓宽交流电机调速范围的理论用到永磁同步电机中，进行了相关理论推导及说明，在MATLAB/Simulink中搭建仿真平台，将一台永磁同步电机绕组进行重新加工，并搭建实验平台，最终从实验所获得的数据验证了利用绕组变匝数理论，在永磁同步电机控制系统改变不大的情况下能够大幅拓宽电机调速范围，满足低速大转矩、高速小转矩的特性，而且控制方法简单，扩大的速度范围与减少的绕组匝数成正比，并且用IGBT来控制切换具有响应时间短，无噪声的特点，整个系统有较好的实用价值。

[1] 沈蕾,孙伟,钱儿,等.双绕组永磁同步电动机冗余控制与故障分析[J].微特电机,2011,39(12):16-18.

[2] 孙东森,葛宝明,毕大强.极相调制异步电机的绕组设计及性能比较[J].电机与控制学报,2010,14(8):81-86.

[3] 陶华堂,李强.基于矢量控制的感应电机弱磁控制算法研究[J].电气传动,2016,46(3)：7-11.

[4]TAKATSUKAY,HARAH,YMADAK,etal.AwidespeedrangehighefficiencyEVdrivesystemusingwindingchangeovertechniqueandSiCdevices[C]//InternationalPowerElectronicsConference,IEEE.2014：1898-1903.

[5]SWAMYMM,KUMET,MAEMURAA,etal.ExtendedhighspeedoperationviaelectronicwindingchangemethodforACmotors[J].IEEETransactionsonIndustryApplications,2006,42(3):742-752.

[6]KUMET,SWAMYMM,SAWAMURAM,etal.Aquicktransitionelectronicwindingchangeovertechniqueforextendedspeedranges[C]//IEEEPowerElectronicsSpecialistsConference,2004:3384-3389.