作业水深对半潜平台气隙影响的比较研究

沈中祥，刘寅东，霍发力，张 健，聂 炎

（1.大连海事大学 船舶与海洋工程学院，辽宁 大连 116026；2.江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；3.戈朗（中国）海事技术咨询公司，上海 201206）

0 引 言

半潜式平台气隙是指其甲板箱底部、救生艇底部等部位与水面之间的垂向间距，其作为平台设计的一个重要指标，对平台安全服役至关重要。当气隙小于零，意味着波浪砰击了平台水面上结构，砰击严重的情况会导致平台结构损坏，威胁平台和人员的安全。在复杂海洋里服役的半潜平台，必须由定位来控制其在海上的位置，以保证恶劣海况下的安全作业。目前，半潜平台最为广泛采用的定位方式主要有锚泊定位系统（Mooring System）、动力定位系统（Dynamic Positioning System，DP）和DP辅助锚泊定位系统（Automatic Thruster Assistance System，ATA）。半潜平台气隙运动极为复杂，与平台的运动响应以及外界载荷密切相关，尤其是平台承受着线性和非线性叠加的波浪载荷，且受平台多立柱和浮箱复杂的绕射和反射，以及平台运动产生的兴波影响，这些因素叠加到入射波上会使波面局部波高明显增加，使得平台气隙降低[1]。

近几年，工程界与学术界对浮式平台气隙进行了大量的理论和实验研究。Kazemi和Incecik等[2]基于混合边界元方法、加权残值理论的直接边界元方法对半潜式平台的气隙性能进行了初步预报。王志东等[3]基于势流理论开展了半潜式平台气隙分布及气隙量的数值预报，定量研究了半潜式平台在不同浪向角特征周期及有义波高情况下对气隙量的影响。姜宗玉，崔锦[4]应用三维源汇分布方法，计算得到半潜式平台在波浪中六自由度运动响应函数以及设定计算位置点处的波面升高响应函数，对平台的气隙响应进行预报。Matsumoto等[5]比较分析了几种设计陡波下的较大低频运动（垂荡、横摇与纵摇）对动态气隙量的影响。Huo等[6-10]提出了在时域中进行非线性气隙和波浪砰击载荷相对于流体载荷的敏感性分析研究，同时研究了风和流的速度与方向等参数对平台气隙运动的灵敏度分析，并基于势流理论修正的CFD方法对平台气隙响应进行了研究。Shen等[11]就锚泊系统特性对平台气隙的影响研究做了比较分析，分析结果显示锚泊系统参数对平台气隙运动有着显著影响。

浮式平台作业水深从几百米到几千米，水深对平台人员安全、工作环境以及水动力性能都有一定的影响。国内外部分学者就水深对海洋结构的运动与水动力性能的影响进行了研究。Andersen[12]考虑船舶服役于有限水深，对其波浪载荷和运动响应进行了研究。肖龙飞等[13]基于数字模拟和模型试验的方法，对FPSO在浅水中低频运动响应进行了研究。吴晞等[14]基于有限水深的三维势流理论，对某船进行了不同水深条件下的纵摇和垂荡RAO计算。谢永和、杨建民等[15]基于缩尺比FPSO模型，考虑了水深对其波浪载荷的影响。霍发力等[16-18]就水深对半潜式平台水动力性能、波浪载荷以及运动响应、设计波以及波浪砰击影响的敏感性进行了研究。

平台在相同的环境载荷下，定位方式不同以及作业水深差异会影响到平台的运动响应，导致平台负气隙产生差异。因此，定位方式以及作业水深对平台气隙和波浪砰击的影响成为平台设计研究的一个重要部分。本文结合水池试验结果，对数值模型进行了粘滞曳力和辐射阻尼修正。考虑平台所受的风、浪、流载荷以及全尺寸锚泊系统对平台运动的影响，运用试验修正数值模型参数的时域全耦合分析方法，对锚泊定位和ATA定位平台在不同作业水深下的气隙响应进行研究。

1 平台运动数学模型及气隙预报理论

1.1 平台运动数学模型

浮式结构在海上定位作业时产生六自由度运动，必然受到各种外力的作用，通常包括：风、浪、流等所产生的海洋环境载荷，锚链张力、推进器推力、运动阻尼等共同作用时会产生低频运动和高频运动。一阶波浪力主要引起高频运动，易导致平台周期性的往复运动，但是平台位置不会受明显影响，因此，我们在研究动力辅助锚泊定位系统时一般只考虑平台的低频运动，对于高频运动一般是忽略的[18]。浮式平台动力辅助锚泊定位系统低频运动模型如下式所示：

式中：系统质量（包含附加质量）矩阵用M表示，水动力阻尼矩阵用D表示。

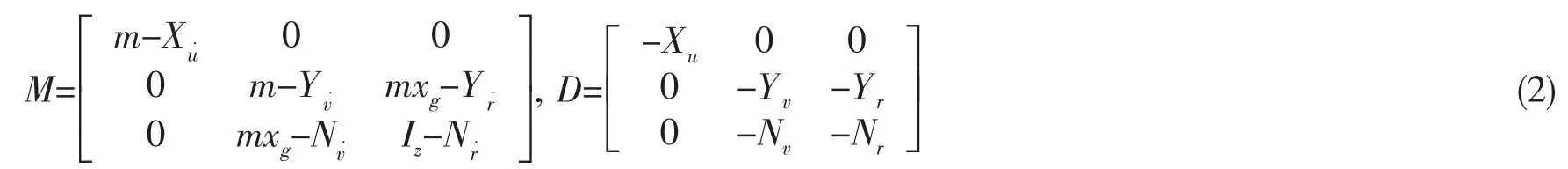
式中：m表示平台总质量；CRB（v）、CA（vr）表示回复力矩阵；Xu˙、Yv˙、xg表示平台中心和重心间的距离，一般取为 0；Iz表示转动惯性矩阵；Yr˙、Nv˙、Nr˙为附加质量系数；Xu、Yv、Yr、Nv、Nr为水动力系数；τ表示外界环境载荷，包括风平均载荷、二阶波浪漂移力和流平均载荷；τthr表示推进器的推力；τmo表示锚链张力。我们可以假定动力辅助锚泊定位系统平台的运动速度很小，即CRB（v）和CA（vr）等同于零。（1）式则可简化为下式[18]：

1.2 气隙预报理论

气隙是指海洋平台甲板底部、救生艇平台底部等位置与水面之间的垂向间隙，如图1所示。平台在波浪中运动的t时刻的气隙a（）t由三部分组成，按下式计算：

式中：a0为静水气隙；η（t）为响应波高；δ（t）为平台垂向位移；r（t）为相对波面升高。

响应波高η（t）常常显示出非线性特性。一般情况下，η（t）是入射波ηi和绕射波ηd的总和，每一个都是假定为一阶和二阶部分的总和，即：

响应波高与平台垂向位移之差为相对波面的升高，平台垂荡、纵摇和横摇三部分运动组成其垂向位移。相对波面升高和平台垂向位移分别按下式计算：

式中：ξ1、ξ2、ξ3分别为平台的垂荡、横摇和纵摇广义位移。

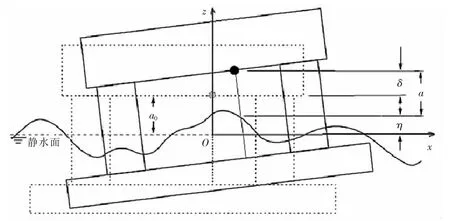
图1 气隙的定义Fig.1 Air gap variable definition

2 平台模型试验和数值模型修正

2.1 数值模型

平台的主要尺寸参数如表1所示，三维模型如图2所示，平面元模型如图3所示。平台采用悬链线式八点对称的锚泊系统进行定位，锚泊系统布置如图4所示。

表1 平台主要参数Tab.1 The parameters of the platform

图2 平台三维模型Fig.2 The 3 d model of platform

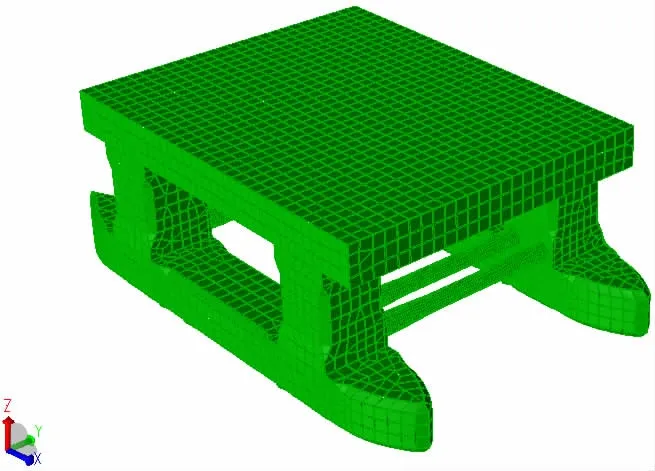
图3 平台面元模型Fig.3 The panel model of platform

2.2 数值模型修正

辐射阻尼是描述流固耦合作用的固有阻尼，而粘滞曳力既是平台运动的阻尼力也是激振力。因此粘滞曳力和辐射阻尼在平台运动响应分析中是不可缺少的部分，彼此不能够互相替代。为了深入研究不同作业水深下平台气隙运动响应，对平台数值模型参数进行修正，以进一步精确模拟平台的运动响应。

2.2.1 模型试验

试验是在拖曳水池中用缩尺比模型进行。水池试验平台模型几何相似比为1：38.9。平台模型与真实平台之间在运用几何、时间等相似的前提下，还要保证模型与平台的Froude数相似，通过多次测量取其平均值来消除偶发事件引起的测量误差。

2.2.2 模型修正

（1）数值模型固有周期

平台在静水中的固有周期是衡量其水动力性能的重要指标。在静水条件下试验和数值计算平台的固有周期见表2。由表中可知，数值计算和试验测试的平台垂荡、横摇和纵摇在静水中的固有周期较为接近。

图4 锚链系统布置图Fig.4 The arrangement of chain mooring system

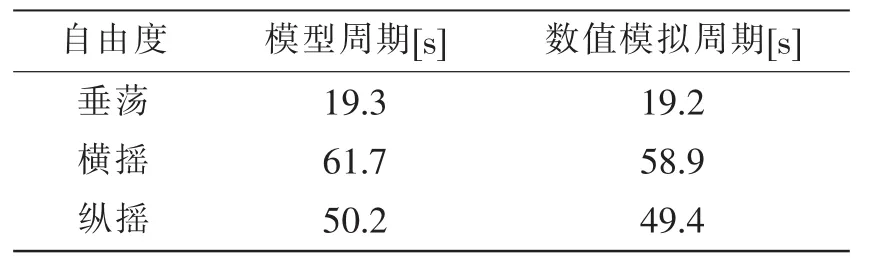
表2 静水情况下平台运动周期比较Tab.2 Comparison of the natural periods in still water

（2）粘滞曳力和辐射阻尼

图5 试验模型与锚泊固定系统Fig.5 The test model and mooring system

根据 DNV-RP-C205（2010）[19]和结构的几何尺寸，Morison单元取得恰当的拖曳力系数，对于Disc单元，在水平和垂直方向上取得不同的系数。运用Morison单元和Disc单元来调整数值模型。通过增加辐射阻尼，来修正平台的数值模型。针对试验中使用的一种工况（有义波高Hs=17.28 m，跨零周期Tz=16.5 s），通过多组的模拟比较，根据与水池试验结果比较最后取3e9 Nm/（rad/s）作为增加纵摇的辐射阻尼。

（3） 锚泊力

根据水池试验测得的锚泊系统的线性刚度，在数值模拟中运用弹簧单元来模拟锚泊系统。数值模拟计算出锚泊系统的水平锚链张力与水池试验在相同工况下测得锚链张力进行比较，如图6所示，结果表明锚泊系统的数值模拟与水池试验非常相近。

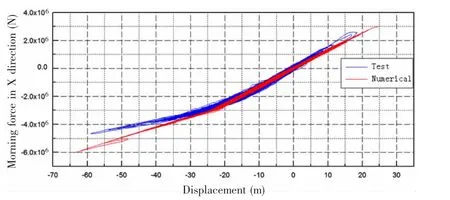
图6 锚泊系统在X方向上受力的比较Fig.6 Comparison of mooring force in X direction

（4）平台运动响应

对修正后的平台数值模型在时域范围内进行了运动模拟，模拟结果与水池试验结果进行了比较。平台在尾迎浪工况下的纵摇和垂荡运动响应时域和频域分析如图7和图8所示，并和水池试验结果进行了对比。由比较结果可知，3e9 Nm/（rad/s）作为增加纵摇的辐射阻尼的数值模型模拟的纵摇结果与水池试验结果非常相近。

根据试验模型与数值模型的相关分析结果比较可知，模型的固有频率、波浪、锚泊系统和运动响应都比较相近，因此，修正后的数值模型可以较好地进行平台数值模型的运动响应模拟。

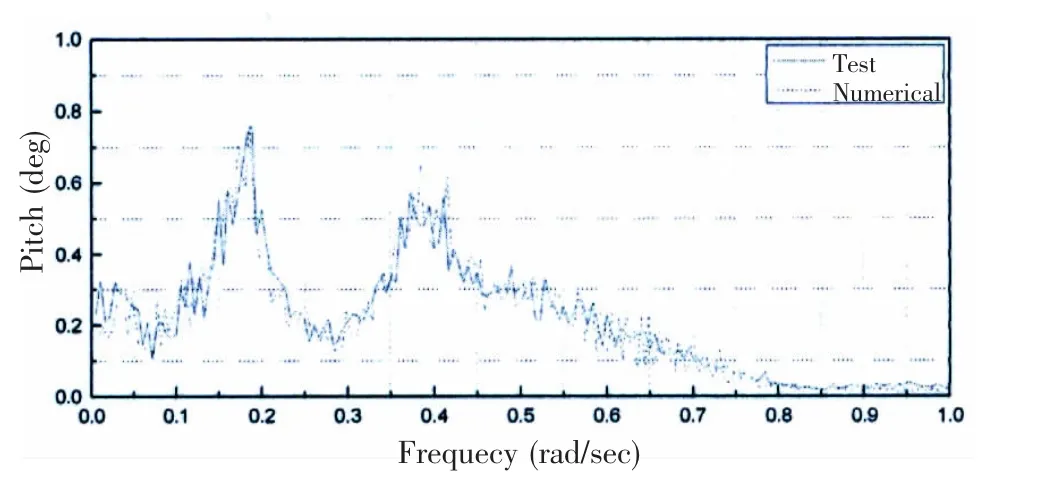
图7 平台纵摇运动响应比较Fig.7 Comparison of pitch motion response

3 环境载荷和海况

半潜式平台环境载荷主要是指风、浪、流、潮汐、地震、海冰等自然环境引起的载荷。根据船级社规范以及设计经验，锚泊分析主要考虑风、波浪以及海流的环境载荷。

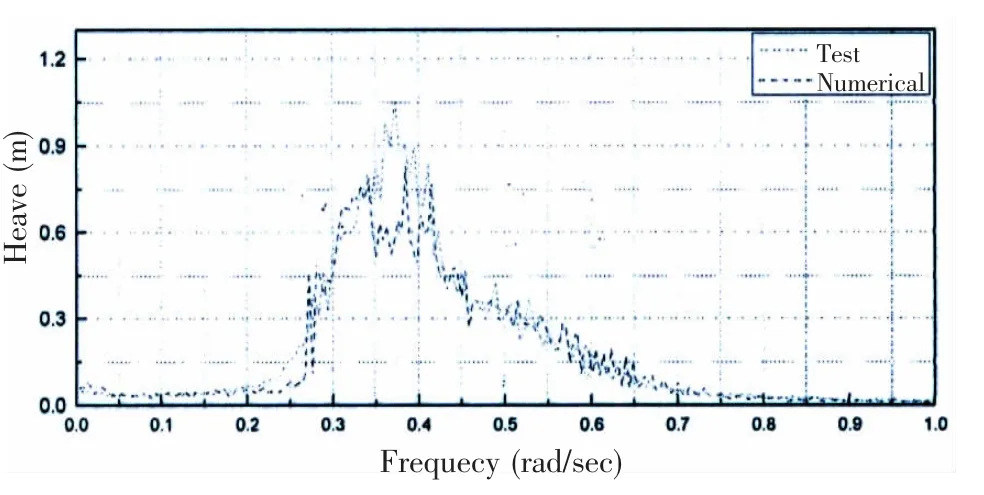
图8 平台垂荡运动响应比较Fig.8 Comparison of heave motion response

3.1 风载荷

根据规范和经验公式，作用在平台上的风载一般由下式来计算：

式中：Fw为风载荷，N；Ch为结构物的高度系数；Cs为结构物的形状系数；A为结构物垂直于风向的轮廓投影面积，m2；Vw为设计风速，m/s。

3.2 海流载荷

半潜式平台流载大小一般由下式来计算：

式中：Fcs为流载，N；Css为半潜式平台流载系数，515.62 Ns2/m4；Cd为拖曳力系数；Ac和 Af分别是圆柱型和扁平型结构总的投影面积。

3.3 海况与观测点

该平台采用北大西洋海况进行计算分析，运用CMA和IFORM方法结合波浪的极限波陡计算设计了北大西洋100年一遇的海况，本节计算选取Hs=17.28 m，Tz=16.5 s。研究平台在自存工况下气隙响应。浪向角是指浪向与X轴正向的夹角，如图9所示。为便于观测平台在各工况下的气隙变化量，在平台甲板箱上布置了7个观测点，观测点主要位于平台甲板箱的下边缘，观测点分布见图10。

图9 半潜式平台入射波浪浪向角示意Fig.9 Incident wave angle diagram

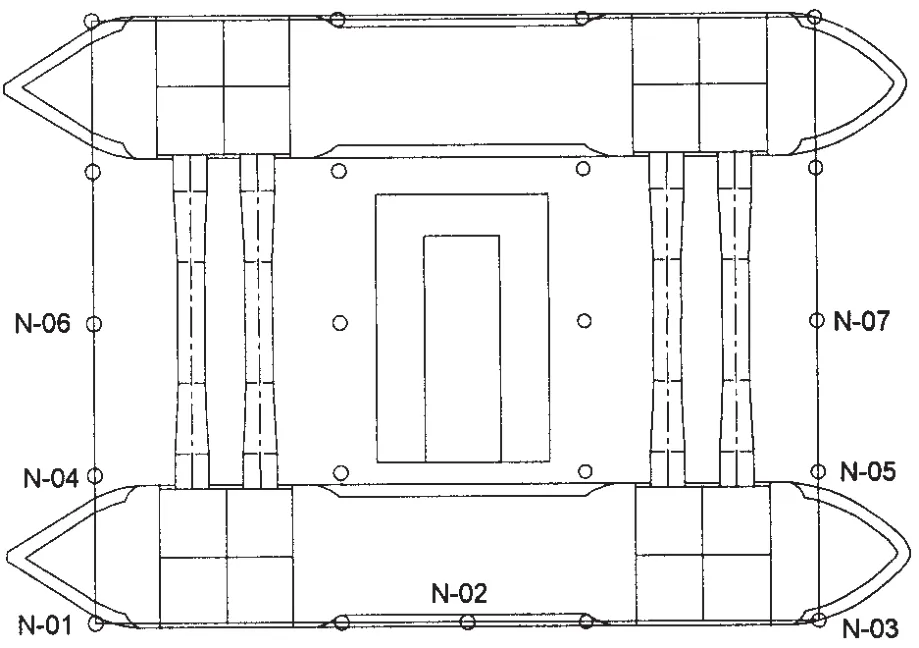
图10 甲板气隙关注点位置示意图Fig.10 The interest points for air gap in deck box bottom

根据DNV-RP-C205[19]规定，峰值周期Tp与跨零周期Tz关系如下：

其中：γ定义如下：

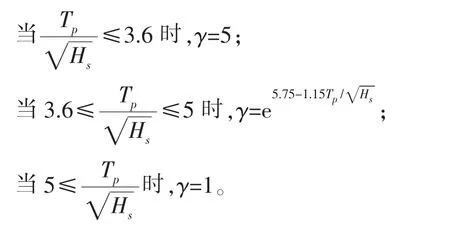
4 不同工作水深下平台时域耦合计算

4.1 分析工况

根据修正的数值模型，在相同的锚链预紧力、锚链长度和环境载荷工况下分别选取了4组工况，比较不同定位方式下平台气隙响应。工况条件如表3所示，其中A-Case表示ATA定位方式，B-Case表示锚泊定位方式。

表3 各工况细节Tab.3 The detail of analysis cases

4.2 计算结果

考虑到时域内模拟波浪的不稳定性，对每组工况分别选取10段不同的随机波浪海况作为该工况下的子工况，每个子工况模拟时间为3 h，各工况中10个子工况所运用的随机波浪是相同的。ACase01-02工况以及B-Case01-02工况下的平台最小气隙响应的平均值计算结果见表4。由表中可知，在斜浪下ATA定位平台的关注点最小气隙响应的平均值N-01、N-04和N-06的负气隙值从500 m水深下的-4.954 m、-2.927 m和-2.154 m改善到300 m水深下的-3.114 m、-0.779 m、-0.215 m；在斜浪下锚泊定位平台的关注点最小气隙响应平均值N-01、N-02、N-03、N-04和N-06的负气隙值从500 m水深下的-4.648 m、-1.107 m、-1.618 m、-1.750 m和-1.548 m改善到300 m水深下的-4.515 m、-1.004 m、-1.440 m、-1.614 m和-1.174 m；由此可见，作业水深对平台气隙影响显著。

表4 最小气隙响应的平均值Tab.4 The mean value of min air gap response

4.3 影响分析

为了进一步探讨不同作业水深下的定位方式对平台气隙响应的影响，分别进行了平台关注点砰击次数统计、关注点气隙预报以及平台响应时域值能量分析。

4.3.1 关注点砰击次数统计

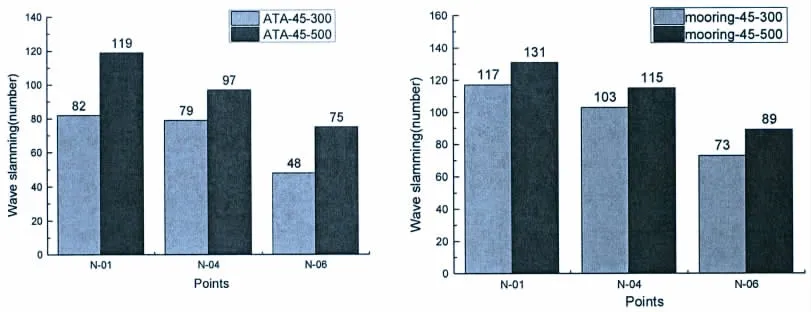
图11 关注点砰击次数统计图Fig.11 The slamming frequency staistics of interest points

图11（a）、（b）依次为45°工况下ATA定位与锚泊定位平台的关注点平均气隙变化图。如图所示，在同等的ATA定位方式下，500 m工作水深下的关注点N-01砰击次数较之于300 m工作水深关注点N-01砰击次数增加37次，增加幅度为31%；N-04关注点增加了18次，增加幅度为18.6% ；N-06关注点增加了27次，增加幅度为36%。在同等锚泊定位方式下，500 m工作水深下的关注点N-01砰击次数较之于300 m工作水深关注点N-01砰击次数增加了14次，增加幅度为10.7%；N-04关注点增加了12次，增加幅度为10.4%；N-06关注点增加了16次，增加幅度为17.9% 。

由上述计算数据可知，平台在同等的环境载荷、预紧力工况下，关注点处波浪砰击次数随着工作水深的增加而加剧。

4.3.2 关注点气隙预报

图12（a）、（b）分别为ATA定位与锚泊下平台在不同作业水深的关注点平均气隙变化图。由图12（a）所示，关注点N-01的负气隙平均值从500 m水深时的-4.954 m增值到300 m水深时的-3.114 m，增值1.84 m，增值幅度37.1%；关注点N-04的负气隙增值2.148 m，增值幅度73.4%；关注点N-06的负气隙增值1.939 m，增值幅度90%。由图12（b）所示，关注点N-01的负气隙平均值从500 m水深时的-4.648 m增值到300 m水深时的-4.515 m，增值0.133 m，增值幅度2.86%；关注点N-04的负气隙增值0.136 m，增值幅度7.8%；关注点N-06的负气隙增值0.374 m，增值幅度24%。由此可见，工作水深的变化对平台负气隙有着显著影响。

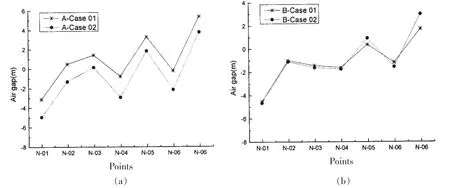
图12 关注点的平均气隙值Fig.12 The average air gap values of interest points

4.3.3 平台响应时域值能量分析

为了进一步分析水深对不同定位方式的平台气隙响应的影响，选取A/B-Case01、A/B-Case02工况中的第一个子工况进行分析。选取发生负气隙的关注点N-01、N-04和N-06作为研究对象，对平台响应的时域值进行能量分析。图13（a）至（f）依次为ATA定位和锚泊定位下平台横摇、纵摇以及垂荡运动响应能量谱。图14（a）至（f）依次为ATA定位和锚泊定位下关注点N-01、N-04和N-06处的气隙响应能量谱。

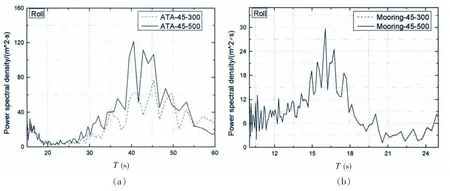
图13 平台横摇、纵摇、垂荡运动响应Fig.13 Response spectral of rolling,pitching and heaving motion

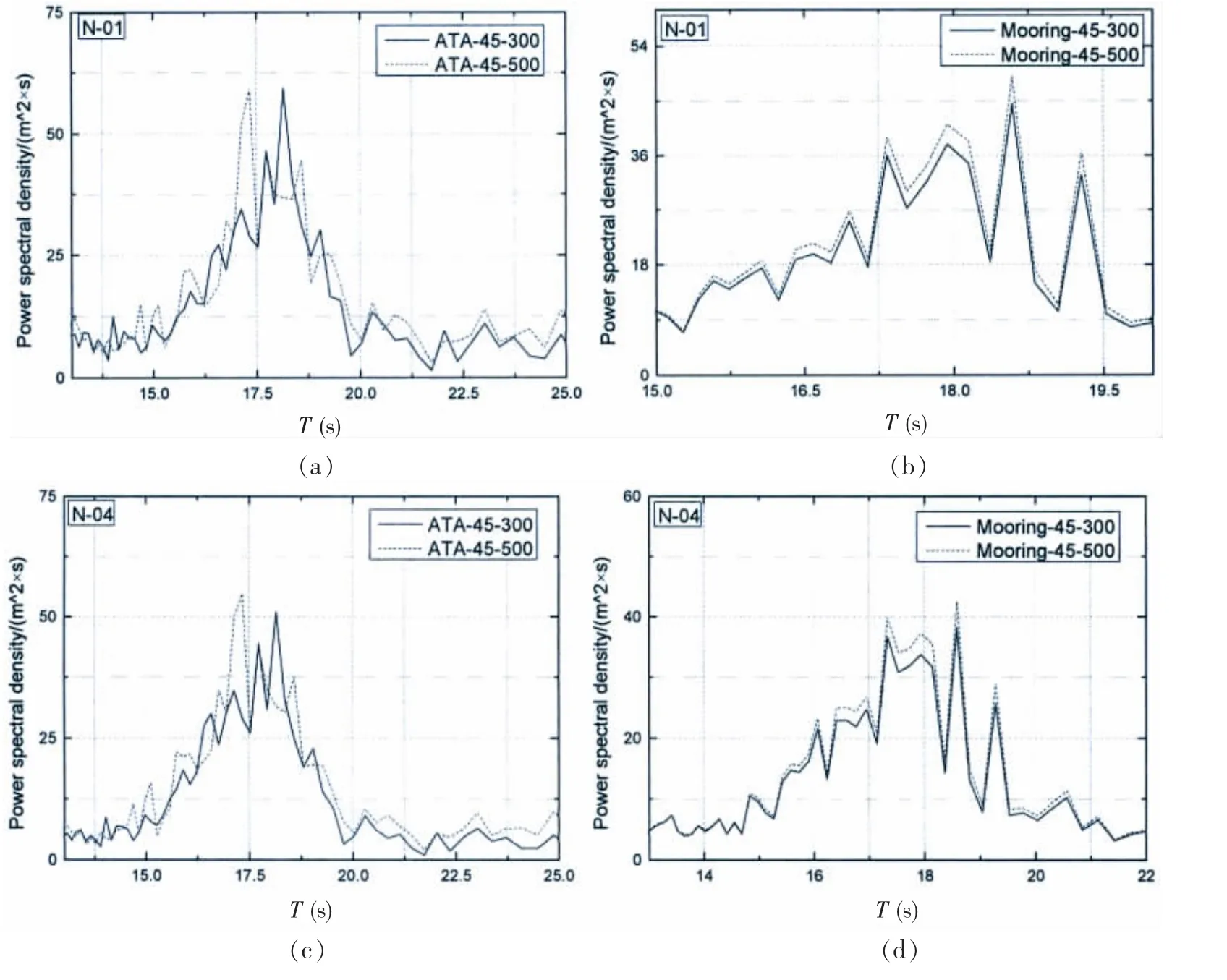
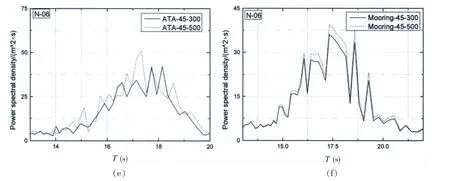
图14 关注点处的气隙响应能量谱Fig.14 Air gap response spectrum at the interest points

5 不同工作水深下平台波浪砰击比较分析

为了进一步比较不同水深下的平台关注点气隙变化情况，分别选取两种定位方式下的平台的气隙关注点在不同作业水深时波浪砰击的变化次数、变化幅值以及负气隙的增值、变化幅值进行比较分析。A-Case 01-02为ATAT定位下平台在两种作业水深的气隙及波浪砰击变化；B-Case 01-02为锚泊定位下平台在两种作业水深的气隙及波浪砰击变化。表5为平台波浪砰击次数增值表；表6为平台气隙增值表；图15（a）为不同工作水深的平台波浪砰击次数对比图，图15（b）为砰击次数变化幅值比较；图16（a）为平台气隙变化对比图，图16（b）为气隙变化幅值的比较。

由表5和图15可知，在同等环境载荷工况下的ATA定位方式平台，关注点N-01在300 m工作水深下的波浪砰击次数较之于500 m工作水深关注点N-01砰击次数减小了37次，减小幅度为31%；N-04砰击次数减小了18次，减小幅度为18.6%；N-06砰击次数减小了27次，减小幅度为36%。在同等环境载荷工况下的锚泊定位方式平台，关注点N-01在300 m工作水深下的波浪砰击次数较之于500 m工作水深关注点N-01砰击次数减小了14次，减小幅度为10.7%；N-04砰击次数减小了12次，减小幅度为10.4%；N-06砰击次数减小了16次，减小幅度为17.9%。

表5 平台波浪砰击次数增值表Tab.5 Increment of wave slamming on platform

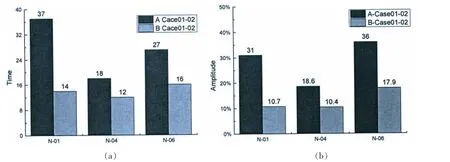
图15 平台波浪砰击比较Fig.15 Comparison of wave slamming on platform

由表6和图16可知，在同等环境载荷工况下的ATA定位方式平台，关注点N-01在300 m工作水深下的波浪砰击次数较之于500 m工作水深关注点N-01气隙值改善了1.84 m，改善幅度为37.1%；N-04气隙值改善了2.148 m，改善幅度为73.4%；N-06气隙值改善了1.939 m，改善幅度为90%。在同等环境载荷工况下的锚泊定位方式平台，N-01气隙值改善了0.133 m，改善幅度为2.86%；N-04气隙值改善了0.136 m，改善幅度为7.8%；N-06气隙值改善了0.374 m，改善幅度为24%。

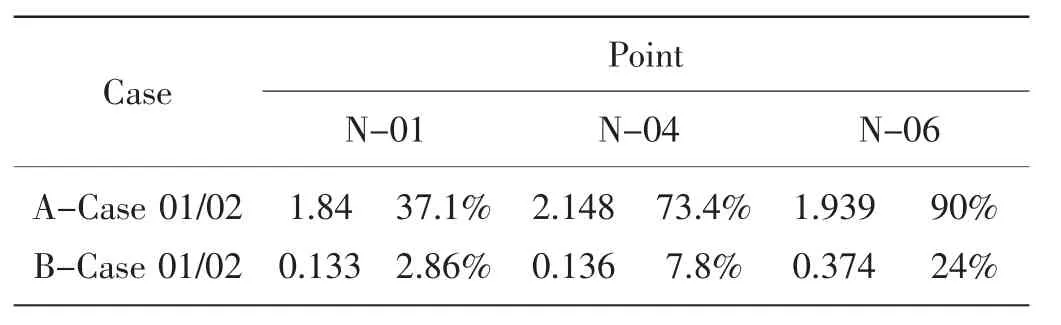
表6 平台气隙增值表Tab.6 Increment of air gap on platform

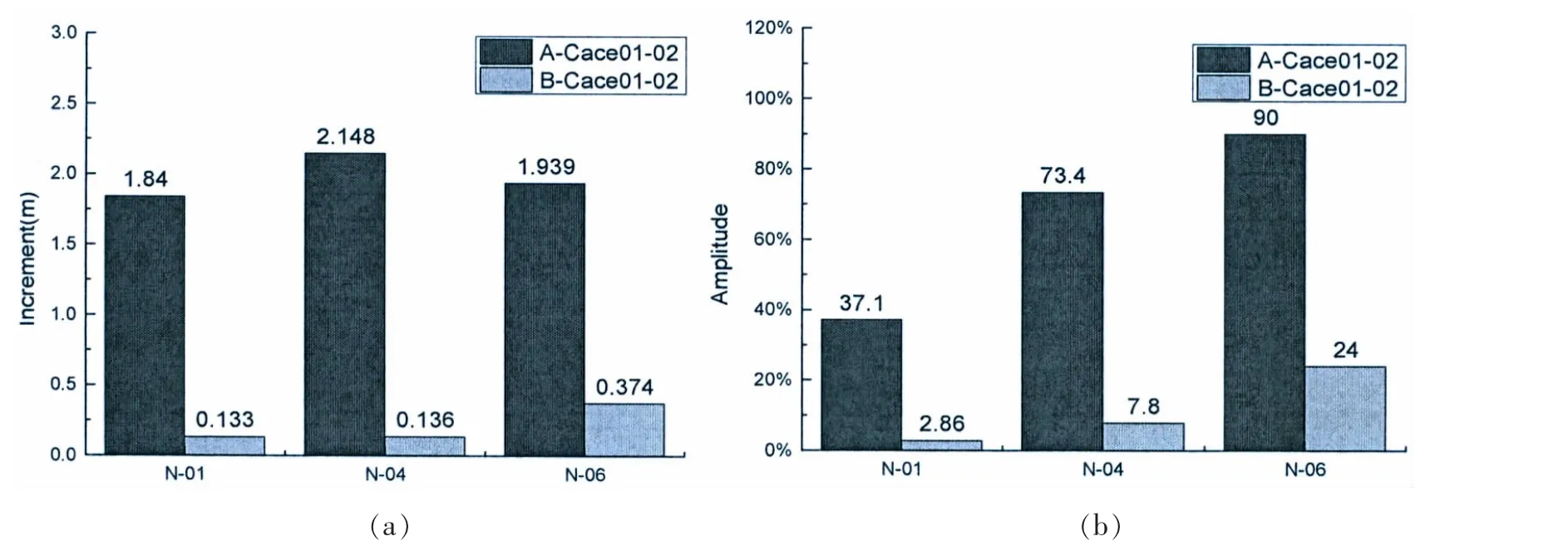
图16 平台气隙变化比较Fig.16 Comparison of air gap changes on platform

由上述计算分析可知，在相同的环境载荷、预紧力工况下，工作水深对关注点处最小气隙和波浪砰击具有显著影响。工作水深变化引起的ATA定位下同一关注点的砰击次数以及改善幅值明显优于锚泊定位方式。工作水深变化引起的ATA定位下同一关注点的气隙变化以及改善幅值也同样明显优于锚泊定位方式。这说明了在风浪流载荷作用下，ATA定位平台较之于锚泊定位平台的随动性更好，可以有效地减小平台与水质点的相对运动。

6 结 论

由于半潜平台作业水深范围很广，并且不同作业水深下平台锚泊系统的刚度发生变化，从而导致平台气隙响应发生差异。针对半潜式平台不同定位方式以及作业水深差异的特点，运用试验结果修正数值模型参数的平台时域全耦合分析方法，并以平台的300 m和500 m作业水深为例，就锚泊定位与动力辅助锚泊定位分别对平台气隙响应的影响进行研究。根据分析结果，可以得到如下结论：

（1）平台在同等环境载荷、预紧力工况下，关注点处负气隙以及波浪砰击次数随着工作水深的增加而加剧。较之于锚泊定位，工作水深对ATA定位下平台的运动响应能量谱、关注点气隙响应能量谱影响更为显著。

（2）不同工作水深对平台的气隙和波浪砰击存在着显著影响。在同等环境载荷工况下，ATA定位平台较之于锚泊定位平台的随动性更好，可以有效地减小平台与水质点的相对运动。工作水深变化引起的ATA定位平台同一关注点的砰击次数、气隙变化以及改善幅值明显优于锚泊定位方式。

参 考 文献：

[1]Kazemi S,Incecik A.Experimental study of air gap response and wave impact forces of a semi-submersible drilling unit[C]//25th international Conference on Offshaore Mechanics and Arctic Engineering.Hamburg,Germany,2006,OMAE2006-92083.

[2]Kazemi S,Incecik A.Numerical prediction of air gap response of floating offshore structures using direct boundary element method[C]//Proceedings of 24th International Conference on Offshore Mechanics and Arctic Engineering,(OMAE2005).Halkidiki.Greece,2005,1：803-809.

[3]王志东,刘美研,凌宏杰.半潜式平台气隙量数值预报方法研究[J].海洋工程,2015,33(5)：10-11.Wang Zhidong,Liu Meiyan,Ling Hongjie,et al.Air gap predication of a semi-submersible platform[J].Ocean Engineering,2015,33(5)：10-11.(in Chinese)

[4]姜宗玉,崔 锦.不规则波中半潜式平台气隙响应数值研究[J].中国海洋平台,2014,29(1)：13-19.Jiang Zongyü,Cui Jin.On numerical investigation of air gap for semi-submersible platform in irregular waves[J].China Offshore Platform,2014,29(1)：13-19.(in Chinese)

[5]Matsumoto F T,Watai R A,Simos A N.Wave run-up and air gap prediction for a large-volume semi-submersible platform[J].Journal of Offshore Mechanics and Arctic Engineering,2013：135/011302.

[6]Huo Fali,Zhang Huixin,Yang Deqing,Cui Jin.Sensitivity analysis of non-linear air gap and wave slamming load with respect to current for semi-submersible platform design[C]//Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference.Hawaii,USA,2015：21-26.

[7]Huo Fali,Zhang Huixin,Yang Deqing,Cui Jin.Sensitivity analysis of wave slamming load with respect to wind load for semi-submersible platform design[J].Shanghai Jiaotong University and Springer-Verlag Berlin Heidelberg,2015,20(4)：385-394.

[8]Huo Fali,Nie Yan,Yang Deqing.Sensitivity analysis of air gap motion with respect to wind load and mooring system for semi-submersible platform design[J].China Ocean Engineering,2016,4：535-546.

[9]Huo Fali,Yang Deqing,Dong Gang.Air gap response study of a semi-submersible platform combining the CFD method and the potential flow theory method[C]//ISOPE(2016).Rhodes,Greece,2016-TPC-0920.

[10]Huo Fali,Zhang Jian,Yang Deqing.Sensitivity study of wave slamming with respect to water depth for floating platform[J].Journal of Shanghai Jiaotong University,2017,51(4)：410-417.(in Chinese)

[11]Shen Zhongxiang,Huo Fali,Nie Yan,et al.Impact analysis of air gap motion with respect to parameters of mooring system for floating platform[J].China Ocean Engineering,2017,2：141-150.

[12]Andersen P.Ship motions and sea loads in restricted water depth[J].Ocean Engineering,1979,6：557-569.

[13]肖龙飞,杨建民,郭 彬.浅水FPSO垂荡和纵摇运动的低频响应[J].舰船科学技术,2009,31(11)：120-124.Xiao Longfei,Yang Jianmin,Guo Bin.Low frequency heave and pitch motions of FPSO in shallow water ship[J].Science and Technology,2009,31(11)：120-124.(in Chinese)

[14]吴 晞,韩晓光,李宇辰.水深对船舶摇荡运动影响的数值方法研究[J].交通信息与安全,2013,177(31)：45-48.Wu Xi,Han Xiaoguang,Li Yüchen.Numerical method for impact of water depth on ship swaying motions[J].Journal of Transport Information and Safety,2013,177(31)：45-48.(in Chinese)

[15]谢永和,李润培,杨建民.水深对超大型FPSO波浪载荷响应影响实验研究[J].海洋工程,2005,23(3)：1-6.Xie Yonghe,Li Runpei,Yang Jianmin.Experimental study on the effects of water depth on wave-induced loads response of a very large FPSO[J].Ocean Engineering,2005,23(3)：1-6.(in Chinese)

[16]霍发力,张 健,杨德庆.工作水深对浮式平台波浪砰击影响的敏感性分析[J].上海交通大学学报,2017,51(4)：410-417.Huo Fali,Zhang Jian,Yang Deqing.Sensitivity study of wave slamming with respect to water depth for floating platform[J].Journal of Shanghai Jiao Tong University,2017,51(4)：410-417.(in Chinese)

[17]霍发力.水深对半潜式平台水动力性能及波浪载荷的影响[J].船舶工程,2014,36(6)：100-103.Huo Fali.Influence of water depth on hydrodynamic performance and wave load of semi-submersible platform[J].Ship Engineering,2014,36(6)：100-103.(in Chinese)

[18]霍发力,张会新,杨德庆.水深对半潜式平台运动响应及设计波的影响[J].中国海洋平台,2014,29(5)：35-40.Huo Fali,Zhang Huixin,Yang Deqing.The effect of water depth on motion analysis and design wave of semi-submersible platform[J].China Offshore Platform,2014,29(5)：35-40.(in Chinese)

[19]王 莉.半潜式钻井平台锚泊辅助动力定位控制研究[D].镇江：江苏科技大学,2016.Wang li.Study on mooring assisted dynamic positioning controlling of semi submersible drilling platform[D].Zhenjiang：Jiangsu University of Science and Technology,2016.(in Chinese)

[20]Det.Norske Veritas AS.DNV-RP-C205 Environmental conditions and environmental loads[M].2010.