基于SPH法的冰与船舶螺旋桨碰撞数值模拟

桂洪斌 ， 胡志宽 ，2

（1.哈尔滨工业大学（威海），山东 威海 264209；2.中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

在我国渤海和黄海北部海域，每年入冬均有大量海冰，冰对船舶与海洋结构物的作用和影响一直受业界的重视。船舶在结冰海区航行时，其螺旋桨裸露在船尾，并且浸入水中深度较浅难以避免与冰发生相互作用，使得桨叶叶梢及叶缘等区域遭受严重的损伤[1]。螺旋桨与冰相互作用主要有两种形式，分别为螺旋桨对冰块（层）的铣削作用和冰块对螺旋桨的冲击作用[2]。铣削作用是在有较大冰块或者冰块困在船体和螺旋桨之间的情况下发生的，此时螺旋桨如同铣削冰块，其产生的负载对螺旋桨桨叶损伤很大。冰冲击现象则是由小尺寸的冰块撞击桨叶引起，且较频繁产生。目前在规范[1，3]中，仅给出螺旋桨与冰相互作用时最大静冰力的计算公式及冰况，主要用于冰区加强型螺旋桨的结构设计以及静力校核等[4]。而冰块对螺旋桨的冲击作用，即冰—桨碰撞问题，是一种瞬态动力响应问题，我国对该问题的研究还非常缺乏。对于此类碰撞动力问题，由于实验代价极高，数值模拟成为冰—桨碰撞研究的一种重要方法。

有限元方法是研究冰与结构物作用的一种重要数值模拟方法。目前，有限元软件如ANSYS/LSDYNA、MSC.DYTRAN等均可用于结构物之间动力作用的数值仿真中，如用ANSYS/LS-DYNA模拟冰与锥体抗冰结构的动力作用过程[5]；用MSC.DYTRAN模拟浮冰撞击LNG船的碰撞过程[6]等。上述冰与锥体结构或LNG船的碰撞均为低速碰撞，而冰与螺旋桨碰撞时，冰块是以很大的相对速度撞击桨叶，给桨叶造成严重的损坏。同时，在高速撞击的过程中，冰将以高的应变率表现为脆性破坏和极端大变形。冰—桨碰撞同鸟撞[7-8]、冰雹冲击问题类似，国内外学者针对鸟撞和冰雹冲击问题均开展了大量的研究工作，主要集中在实验方法和数值模拟方法两个方面。在处理鸟撞和冰雹冲击等高速碰撞问题时，鸟体或冰雹往往会出现极度大变形现象，有限元方法在求解这些工程问题时就变得相当困难。

通过查阅文献，Anghileri等[9]采用Lagrange（拉格朗日）、ALE（任意朗格朗日—欧拉）和SPH（光滑粒子流体动力学）三种方法对冰雹冲击铝板进行了数值模拟和对比。Pernas[10]采用Carney[11-12]等的实验模型，在数值模拟中将冰的数值模型采用自定义本构子程序，基于Lagrange、ALE和SPH三种方法进行数值模拟，其分析结果与Carney的实验数据进行了比对。以上研究发现，基于SPH法的模拟结果较于Lagrange和ALE法更贴切试验结果，计算效率更高，更能较真实模拟结构的极端大变形。SPH法是较突出的一种无网格数值方法，其优点在于它是一种纯Lagrange方法，可避免高维拉式网格方法中的网格缠绕、扭曲、负体积等问题，避免Euler方法难于追踪物质变形的缺点，也避免了ALE方法不断重构网格并增加计算时间的缺点，所以适用于冰—桨碰撞问题中冰的动态大变形模拟。

因此，本文建立了冰—桨碰撞计算模型，基于冰高速撞击桨叶的脆性变形特点，冰模型采用SPH法，桨叶模型采用有限元Lagrange方法，运用非线性有限元软件ANSYS/LS-DYNA，对螺旋桨与冰在不同速度和位置下碰撞和螺旋桨与不同半径冰碰撞下的动态响应进行了研究。

1 冰的数值模型及验证

1.1 冰的数值模型

真实的海冰材质复杂，其本构关系难以描述，并且在撞击桨叶过程中呈现极端大变形现象，导致在碰撞分析中难以对冰建立准确的数值模型。高速冲击下的冰，会涉及到高应变率的问题，冰在应变率增加时会经历一个由韧性转为脆性破坏的转变过程[12]。如何能够较准确模拟冰的失效破坏和确保结构响应的可参考性，冰的数值模型尤为关键。由于冰材质的复杂性，往往在数值模拟中假定冰是一种典型的弹塑性材料，本研究采用Carney等提出的带有失效模式的高应变率的冰数值模型。冰的材料模型采取各向同性弹塑性材料模型，即LS-DYNA材料库中的MAT155（关键词为*MAT_PLASTICITY_COMPRESSION_TENSION_EOS），材料参数、状态方程以及冰的应变率灵敏度等设置参照文献[12-14]。

1.2 高速冰冲击验证

为了验证冰的数值模型和碰撞数值模拟计算方法的可行性，本文参照Carney的实验冲击模型如图1所示，即直径为17.46 mm、长度为42.16 mm的冰柱以一定的速度冲击直径为63.5 mm、长度为19.05 mm的钢柱。在建模过程中，需要特别注意弹簧单元和集中质量单元的建立，弹簧K1、K2、K3的刚度系数和集中质量M在图1已给出。钢柱采用有限元Lagrange网格，假定为刚体（关键字为*MAT_RIGID，只允许纵向位移），密度为8 000 kg/m3，弹性模量为193 GPa，泊松比为0.29。冰模型采用SPH法，SPH模型的建立通过LS-DYNA后处理器LS-PREPOST进行，其单元数为35 800个。冰的冲击速度分别设置为91.44 m/s，152.40 m/s和213.36 m/s。接触算法采用自动点对面接触，时间步长取为0.5。为了便于精确地提取弹簧力时程曲线和输出更多的计算节点，在*DATABASE_OPTION的DEFORCE选项中DT设置为5e-9。另外，弹簧K3的最下端采用刚性固定，弹簧与弹簧、质量、钢柱的连接方式采用共节点形式。计算截止时间为0.2 ms。

最终SPH-FE模型如图2所示。通过对K文件进行求解后，提取弹簧K1的弹簧力时程曲线，对数据进行过滤（滤波频率为25 kHz）。图3分别列出了本文计算的冲击速度为91.44 m/s，152.40 m/s和213.36 m/s下弹簧K1力随时间变化曲线，并与Carney的实验数据等相对比。在0-0.2 ms内，本文计算的数值模拟结果与Carney的实验结果和数值模拟结果吻合较好，同时也验证了冰的数值模型及碰撞计算方法的可行性。图4所示为冰在冲击速度为152.40 m/s下0-0.2 ms内部分时刻冲击示意图，由图中可见冰在高速冲击时出现的极端大变形和粉碎性撞击现象。

图1 冲击模型示意图Fig.1 Impact model

图2 SPH-FE模型Fig.2 SPH-FE model

图3 弹簧K1力时程曲线对比图Fig.3 Spring K1force history results

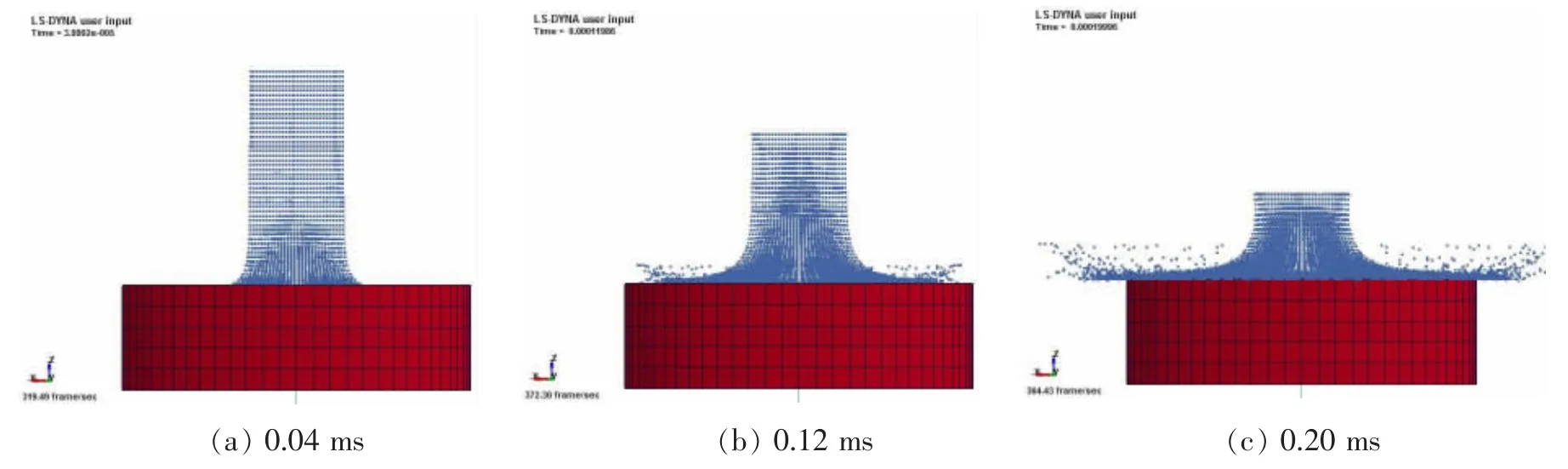
图4 部分时刻冲击示意图（冲击速度为152.4 m/s）Fig.4 Part time impact diagram(velocity：152.4 m/s)

2 冰—桨碰撞的动态响应分析

2.1 冰—桨碰撞的影响因素

冰—桨碰撞过程极其复杂，桨叶损坏的程度主要取决于螺旋桨的几何型式及材料属性、冰块与螺旋桨的碰撞部位及相对速度、冰块几何形状及尺寸、冰的物理力学特性以及海水流体环境等。由于上述涉及到的因素复杂且多具有不确定性，本文忽略海水流体环境和冰块几何形状等影响，冰块假定为球体。根据运动的相对性，假定桨叶不转动，则冰块以高速撞击桨叶，主要考虑相同条件下分别改变冰-桨碰撞速度、位置以及冰的半径单个碰撞参数，对比研究不同碰撞工况下桨叶的变形、单元最大应力以及碰撞过程中产生的碰撞力等响应差异。

2.2 冰—桨碰撞模型建立

桨叶模型的设计参数来源于某沿海单桨散货船螺旋桨，其主要设计参数和材料属性如表1所示。桨叶模型采用有限元Lagrange网格，如图5所示，单元类型选用10节点四面体Solid168单元，单元数为26 281。约束条件是在桨叶0.2R半径处，即叶根处设定为固定约束。冰采用SPH模型，如图6所示，材料参数的设置同本文1.2节。计算终止时间为6 ms。

表1 桨叶设计参数及材料属性Tab.1 Design parameters and material properties of blade

图5 桨叶有限元模型Fig.5 Finite element model of blade

图6 冰SPH模型Fig.6 SPH model of ice

2.3 冰—桨碰撞速度的影响

对于冰-桨碰撞问题，其相对速度是一个很重要的因素。假定半径r为0.10 m的冰球撞击桨叶叶面的0.975R附近区域（叶梢部位）这一碰撞模型，冰的冲击速度方向为螺旋桨的前进方向（沿Z轴正向），速度大小分别为 5 m/s、10 m/s、20 m/s、30 m/s、40 m/s和 50 m/s。

图7和图8所示分别为碰撞速度为50 m/s时部分时刻冰和桨叶的变形云图，可见冰在碰撞过程中受到挤压发生大变形，其变形情况远远大于桨叶的变形情况，主要是因为冰的弹性模量和密度均比螺旋桨小得多。由图8可见，桨叶的最大变形处位于碰撞区域的叶梢部位附近，为了便于观察桨叶的变形，选取叶梢部位的节点348，节点位置如图9所示。不同碰撞速度下该节点的位移时程曲线如图10所示，可见，随着碰撞速度的增大，同等时刻下，桨叶的变形也增大。

图11给出了冰以不同碰撞速度下撞击桨叶的碰撞力随时间的变化曲线。从图11可以看出，碰撞速度越大，其碰撞越剧烈，冰与桨叶越开始接触碰撞，产生的碰撞力越大，碰撞力进入峰值的时间越短。同样，桨叶单元最大应力和最大应变随时间变化曲线分别如图12和图13所示，可见，碰撞过程中短时间内会给桨叶巨大的冲击力，使得桨叶的最大应力和最大应变均迅速增大，并且在同一时刻，碰撞速度越大，桨叶的最大应力和最大应变均越大。

为了更好地观察桨叶局部单元应力的情况，选取叶背表面的单元10016、13824、24824、20463和19420，各单元位置如图9所示。图14给出了碰撞速度为50 m/s时五个单元的应力时程曲线并与桨叶所有单元的最大应力时程曲线对比图。由图14可以看出，在0-1.0 ms内，单元10016的应力接近桨叶所有单元的最大应力时程曲线，说明桨叶的最大应力的区域位于单元10016附近的叶梢部位；同样，在1.5-3.0 ms内，单元13824的等效应力时程曲线接近桨叶所有单元的最大应力时程曲线，这说明在该时间内，桨叶的最大应力处位于单元13824附近的局部区域。以此类推，最大应力值的区域是随着碰撞时间的改变而变化的，随着时间的增加，最大应力值的区域将从叶梢部位逐渐向叶根部位转移。

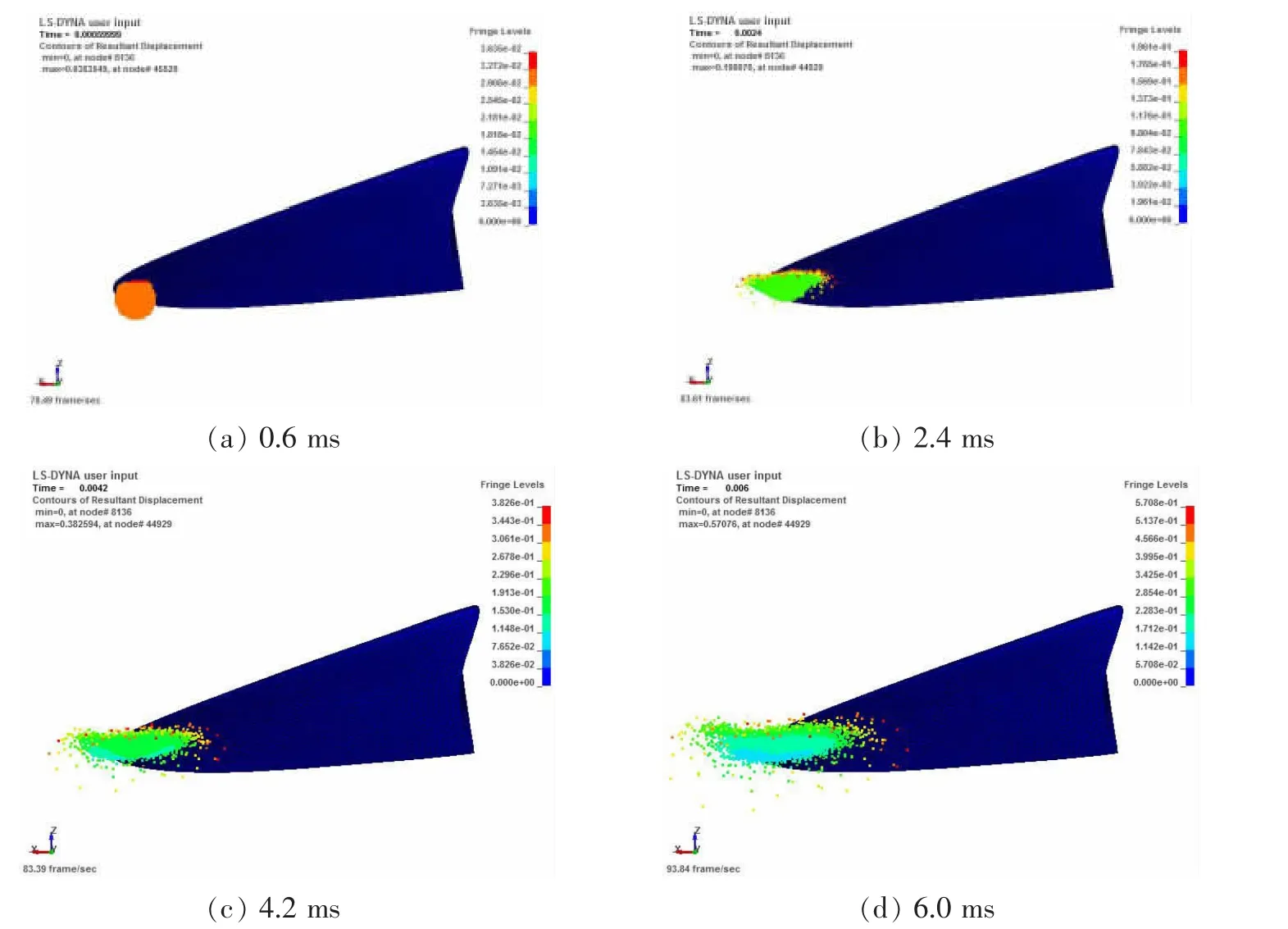
图7 部分时刻下冰的变形云图（V=50 m/s）Fig.7 Part time deformation of ice(V=50 m/s)

图8 部分时刻下桨叶的变形云图（V=50 m/s）Fig.8 Part time deformation of blade(V=50 m/s)

图9 选取节点和单元位置Fig.9 Location of selected node and elements

图10 节点348位移—时间曲线Fig.10 Node 348 displacement-time curves

图12 桨叶单元最大应力—时间曲线Fig.12 Blade elements maximum strain-time curves

图13 桨叶单元最大应力—时间曲线Fig.13 Blade elements maximum stress-time curves

图14 选取单元应力—时间曲线Fig.14 Elements selected maximum stress-time curves

2.4 冰—桨碰撞位置的影响

螺旋桨不仅其曲面高度不规则，而且其厚度各处均不同，使得冰与桨在不同位置发生碰撞时，冰对桨叶的损伤情况不同。显而易见，在相同条件下，桨叶较薄的叶缘区域受到撞击时，最容易受到损害。本文将对表2的三种碰撞计算工况进行模拟和分析。冰的冲击速度方向沿Z轴正向，大小为50 m/s。

表2 各工况碰撞区域Tab.2 Collision postions of each case

三种不同碰撞工况下碰撞力随时间的变化曲线如图15所示。由图15可见，三条曲线差距不大，这是由于选取的三种不同碰撞位置处桨叶的厚度均较薄，碰撞位置对碰撞力的影响不大。但工况1、工况2和工况3的平均碰撞力分别为28.6 kN、27.2 kN和24.5 kN，即碰撞位置离叶根越远，平均碰撞力呈现为略微增加的趋势。

图16所示为三种工况下桨叶单元最大应力时程曲线。图17给出了0.6 ms时刻三种工况下的应力分布云图，工况1的最大应力值最大。这是因为冰与桨叶碰撞的叶梢部位，其厚度和宽度均较小，使得叶梢区域受到撞击时的刚度减少。工况1为典型工况，螺旋桨在高速旋转时，叶梢部位受到冰块撞击的概率最大。此外，碰撞位置同样处于叶缘，其离桨叶叶根越远，桨叶的最大应力值就越大，对桨叶的损伤情况越严重。

图15 碰撞力—时间曲线Fig.15 Impact force-time curves

图16 桨叶单元应力—时间曲线Fig.16 Blade elements maximum stress-time curves

图17 三种工况下桨叶应力分布云图（t=0.6 ms）Fig.17 Blade stress contours of three cases(t=0.6 ms)

2.5 不同半径冰与桨碰撞

碎冰块呈现为无规则的形态，其形状及尺寸千差万别。数值模拟中，假定冰是球形，其半径分别为0.05 m、0.10 m、0.15 m和0.20 m，碰撞位置如表2中的工况1，冲击速度沿Z轴正向，大小为50 m/s。

不同半径的冰球与桨碰撞时节点348的位移时程曲线和碰撞力时程曲线分别如图18和图19所示，可见，随着冰的半径的增大，相同时刻桨叶的变形也增大。同样，冰的半径越大，在碰撞过程中产生的碰撞力就越大。

图20所示为不同半径的冰球与桨碰撞下桨叶单元最大应力随时间变化曲线，在相同条件下，冰的半径越大，则对桨叶的损坏程度就越大。从图20可以看出，冰的半径r为0.20 m时，桨叶单元最大应力值将尽达到500 MPa，因此这样的情况下对螺旋桨的损害是破坏性的。

图18 节点348位移—时间曲线Fig.18 Node 348 displacement-time curves

图19 碰撞力—时间曲线Fig.19 Impact force-time curves

图20 桨叶单元最大应力—时间曲线Fig.20 Elements maximum stress-time curves

3 结 论

本文对冰—桨碰撞问题进行了研究，针对螺旋桨与冰在不同速度、位置下碰撞和螺旋桨与不同半径冰碰撞下的动态响应进行了数值模拟，得出结论如下：

（1）针对高速冰冲击实例，冰模型采用SPH法，验证了冰的数值模型及碰撞数值模拟计算方法的可行性。

（2）冰的冲击速度越大，冰-桨碰撞越剧烈，桨叶的变形、单元最大应力和应变以及碰撞过程中产生的碰撞力均会越大，冰对桨叶造成的损伤情况越大。

（3）位于叶缘处的三种碰撞位置，其离桨叶叶根越远，单元最大应力值就越大，对桨叶的损伤情况越严重。但选取的三种碰撞位置对碰撞力影响不大，碰撞位置离叶根越远，平均碰撞力呈现为略微增加的趋势。

（4）相同条件下，冰的半径越大，即冲击能量越大，桨叶的变形、单元最大应力以及碰撞过程中的碰撞力均越大，对桨叶的损伤情况越大。特别是冰的半径为0.20 m时，桨叶单元最大应力值将尽达到500 MPa，在该工况下对螺旋桨的损害是破坏性的。

由于制约分析结果的因素复杂，本文忽略了流体环境及冰的形状等参数的影响，数值模拟结果难免与实际出现偏差，但定性地得出了不同碰撞速度、位置和不同半径冰对冰-桨碰撞问题的影响规律，可为今后的研究工作打下良好的基础。

参 考 文献：

[1]DNV.Ice strengthening of propulsion machinery[S].2011.

[2]ABS.Guidance notes on ice class[S].2005.

[3]IACS.URI3 machinery requirements for polar class ships[S].2006.

[4]胡志宽,桂洪斌,夏鹏鹏,等.冰载荷下船舶螺旋桨强度的有限元分析[J].船舶工程,2013,35(8)：12-15.Hu Zhikuan,Gui Hongbin,Xia Pengpeng,et al.Finite element analysis of ship propeller strength under ice loads[J].Ship Engineering,2013,35(8)：12-15.

[5]武文华,于佰杰,许 宁,等.海冰与锥体抗冰结构动力作用的数值模拟[J].工程力学,2008,25(11)：192-196.Wu Wenhua,Yü Baijie,Xü Ning,et al.Numerical simulation dynamic ice action on conical structure[J].Engineering Mechanics,2008,25(11)：192-196.

[6]Wang B,Yu H C,Basu R.Ship and ice collision modeling and strength evaluation of LNG ship structure[C].ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering.American Society of Mechanical Engineers,2008：911-918.

[7]刘 军,李玉龙,刘元镛.基于SPH方法的叶片鸟撞数值模拟研究[J].振动与冲击,2008,27(9)：90-93.Liu jun,Li Yülong,Liu Yuanyong.Numerical simulation study of bird-impact on a blade using SPH method[J].Journal of Vibration and Shock,2008,27(9)：90-93.

[8]贾建东,李志强,杨建林,等.用SPH和有限元方法研究鸟撞飞机风挡问题[J].航空学报,2010,31(1)：136-142.Jia Jiandong,Li Zhiqiang,Yang Jianlin,et al.A study of bird impact on aircraft windshield using SPH and finite element method[J].Acta Aeronautica et Astronautica Sinica,2010,31(1)：136-142.

[9]Anghileri M,Castelletti L M L,Invernizzi F,et al.A survey of numerical models for hail impact analysis using explicit finite element codes[J].International Journal of Impact Engineering,2005,31(8)：929-944.

[10]Pernas-Sánchez J,Pedroche D A,Varas D,et al.Numerical modeling of ice behavior under high velocity impacts[J].International Journal of Solids and Structures,2012,49(14)：1919-1927.

[11]Carney K S,Benson D J,Du Bois P,et al.A high strain rate model with failure for ice in LS-DYNA[C].Proceedings of the Ninth International LS-DYNA Users Conference.2006：4-6.

[12]Carney K S,Benson D J,DuBois P,et al.A phenomenological high strain rate model with failure for ice[J].International Journal of Solids and Structures,2006,43(25)：7820-7839.

[13]Keegan M H,Nash D,Stack M.Numerical modelling of hailstone impact on the leading edge of a wind turbine blade[J].EWEA Annual Wind Energy Event 2013,2013.

[14]Hu Zhikuan,Gui Hongbin,Xia Pengpeng,et al.Dynamic response analysis of the collision between ice and propeller at high speed[C].The Society for Underwater Technology Conference(SUTTC 2013),2013：72-76.