高铁隔震桥梁模拟地震振动台试验研究

吴 迪，戴隆华，臧晓秋，熊 焱，吴成亮

(1.广州大学 工程抗震研究中心，广东 广州 510405;2.中国铁道科学研究院，北京 100081;3.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640;4.鑫拓力工程技术有限公司，湖北 武汉 430073)

桥梁结构采用减隔震技术，能够减少高速铁路桥梁上部结构响应和墩底弯矩，在很大程度上提高了桥梁在地震作用下的安全性，减小因地震造成的桥梁损害[1-2]。1985年美国学者ZAYAS[3]首先提出摩擦摆支座这一概念，该支座具有承载能力高、位移大、耐久性强、自动复位的优点，还具有良好的稳定性。此后，摩擦摆支座作为一种新型的隔震支座被成功应用于大量的实际工程中[4-6]。PENG等[7]对采用双曲面隔震支座的连续梁桥减震效果进行了研究。WEI等[8]研究了拉索摩擦隔震支座对多跨连续梁桥的抗震性能的影响。刘健新等[9]对桥梁结构的减震装置、减震设计方法等进行了研究。黄宇辰[10]通过对高铁隔震桥梁在正常使用状态以及地震作用下的结构响应进行分析，研究了摩擦摆支座在高铁桥梁减隔震设计中的适用性。杨林等[11]通过振动台试验与有限元模型对比分析，认为摩擦摆隔震装置能够有效减少地震对上部结构的影响，隔震效果明显。

我国高铁桥梁结构应用隔震技术仅限于试点阶段，李冰等[12]通过数值仿真分析发现地震动参数等因素对隔震效果会有一定影响，有待对摩擦摆支座高架桥梁结构进行试验研究、理论分析。因此，本文以我国常用高铁桥梁设计的标准桥梁类型为例，对单跨32.5 m 高铁简支梁桥进行缩尺设计、制作和安装，并进行地震模拟振动台试验，以研究不同地震波激励下摩擦摆支座的动力响应规律和减隔震性能。

1 双凹面摩擦摆支座力学计算和试验

1.1 双凹面摩擦摆支座的简化力学计算

单球面摩擦摆支座是由上支座组件、下支座组件和1个滑块组成。单球面摩擦摆系统可以简化为1个沿圆弧面运动的滑块，其受力示意如图1。

图1 单球面摩擦摆支座滑动球面受力示意

根据牛顿第二定律建立滑块与上支座组件在A点垂直于滑动球面半径方向力的平衡方程，即

F1cosθ1-f1-Wsinθ1=ma

(1)

式中：F1为支座承受水平方向的剪力；θ1为滑块的转角；f1为滑块受到的摩擦力；W为支座承受的竖向荷载；m为滑块质量；a为滑块沿圆弧切向的加速度。

滑块质量较小时可忽略其影响，式(1)可变形为

F1=Wtanθ1+f1/cosθ1

(2)

滑块的摩擦力可表示为

(3)

以上各物理量之间的关系如下

(4)

N1=Wcosθ1

(5)

将式(5)代入式(3)可得

(6)

当θ1较小时，则有

tanθ1≈D/R1

(7)

式中：D为滑块的水平向位移；R1为下支座组件滑动面的曲率半径。

将式(6)和式(7)代入式(2)，可得

(8)

同理，当单球面摩擦摆的滑动面位于上支座组件时，支座承受的水平方向剪力F2为

(9)

双凹面摩擦摆支座与单球面摩擦摆支座的构成基本相同，但它的上下支座组件均为圆弧面，那么支座承受的水平方向剪力可表示为

F=F1+F2

(10)

如果上下滑动的圆弧面曲率半径一致，那么F1=F2，式(10)可变形为

F=2F1

(11)

1.2 模型支座的力学性能试验

根据模型试验相似理论[13]与振动台的试验条件，确定本次试验模型与原型相似关系，如表1所示。

表1 试验模型与原型相似关系

根据支座简化力学计算公式和反应谱理论，以及原型高铁桥梁荷载和相似关系，确定本次试验摩擦摆球面的半径为0.8 m，最大水平位移为100 mm，双凹面摩擦摆支座剖面如图2所示。

图2 双凹面摩擦摆支座剖面(单位：mm)

为研究双凹面摩擦摆支座的力学性能参数，采用4个支座同时进行水平低周反复加载试验。支座试验加载采用位移控制，竖向加载40 kN，支座最大水平剪切变形为±45 mm。试验加载位移曲线采用正弦曲线加载，加载频率为0.05 Hz，加载位移如图3所示。双凹面摩擦摆支座试验结果和简化力学计算得到的水平力和位移的滞回曲线如图4所示。可知，支座的试验值和理论值基本一致；反复循环加载测试结果显示摩擦摆支座的性能稳定，且滞回曲线饱满，说明支座的耗能性能良好。

图3 支座加载位移

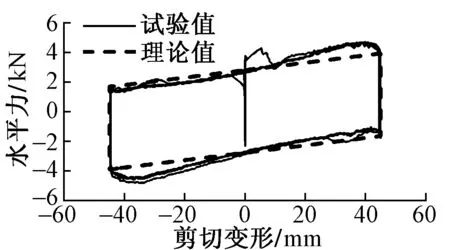
图4 支座的滞回曲线

2 隔震桥梁振动台试验

2.1 模型的设计与制作

模型桥墩高度为1 m，梁体跨度为2.68 m，桥面宽度为0.94 m。模型混凝土选用C30，纵筋选用HRB335。模型墩底及梁截面配筋如图5所示。每个墩顶布置2个摩擦摆支座，分别在梁端底部和墩顶预埋钢板并采用螺栓连接。

模型梁体自重为0.8 t，所需配重为4.2 t。为保证桥墩与振动台固接，桥墩底部浇筑尺寸为1.4 m(长)×0.6 m(宽)×0.2 m(高)的钢筋混凝土连接底座。模型试验情况如图6所示。

图5 模型墩底及梁截面配筋(单位：mm)

图6 模型试验情况

2.2 试验测量方案

为测量在不同地震波激励下桥梁模型的地震响应，在模型的关键部位布置了传感器，见图7。测量内容包括加速度、位移和应变响应。加速度和位移响应测试采用丹麦生产的4381V型电荷加速度计，并配合NEXUS 2692-014电荷放大器进行测量。应变响应测试采用德国HBM公司生产的SPIDER8应变仪，数据采集软件采用其配套软件Catman。在模型墩顶、墩底以及梁体两端均布置了加速度和位移传感器测量模型水平方向的加速度及位移响应；在桥墩底部关键位置布置了应变片测量混凝土和钢筋的应变响应。

图7 桥梁模型传感器布置(单位：mm)

2.3 地震动输入

试验采用MTS公司三向六自由度振动台对模型进行加载，振动台的台面尺寸为3 m×3 m，台面最大位移为100 mm，最大负荷为250 kN，工作频率为0.1～50.0 Hz。试验选取2条符合场地要求的地震动记录：El Centro和汶川地震波。抗震设防烈度分别为8度(0.2g，0.3g)和9度(0.4g)时地震动(顺桥向)加速度反应谱平均值如图8所示。

图8 地震动(顺桥向)加速度反应谱平均值

根据模型的相似关系，地震动加速度峰值0.2g，0.3g，0.4g可换算为0.36g，0.54g，0.72g。采用x向(顺桥向)、y向(横桥向)单向和x+0.85y双向加载。

3 振动台试验结果及分析

3.1 动力特性分析

采用有限带宽白噪声信号对模型激励，从而获取模型的结构模态特征参数，测得桥梁模型x向、y向的固有频率分别为6.88，8.63 Hz。试验前后所测得隔震桥梁模型的自振频率和模态基本一致，说明试验后隔震桥梁模型仍处于弹性状态。由于白噪声激励的强度相对较低，摩擦摆支座并未进入屈服状态，因此结构动力特征分析中得到的隔震桥梁自振频率主要由摩擦摆支座的屈服前刚度决定。

3.2 加速度响应分析

通过对加速度传感器获得的信号进行处理得到不同抗震设防烈度地震作用下模型的响应。在9度(0.72g)El Centro和汶川地震波作用下，顺桥向和横桥向墩底、墩顶和主梁测点与输入地震动加速度峰值之比如图9所示。由于墩底与振动台固接，因此墩底响应与输入地震动加速度峰值之比为1。可知，采用隔震支座后主梁的加速度响应比墩顶和墩底显著降低。

图9 墩底、墩顶和主梁测点与输入地震动加速度峰值之比

图10 不同抗震设防烈度地震作用下主梁加速度峰值

不同抗震设防烈度地震作用下主梁加速度峰值见图10。可知，当抗震设防烈度分别为8度(0.36g)、8度(0.54g)、9度(0.72g)时，El Centro地震波作用下主梁顺桥向加速度峰值分别为输入地震动加速度峰值的31%，22%，19%，横桥向加速度峰值分别为输入地震动加速度峰值的41%，31%，24%。汶川地震波作用下主梁顺桥向加速度峰值分别为输入地震动加速度峰值的27%，19%，15%，横桥向加速度峰值分别为输入地震动加速度峰值的35%，25%，20%。说明随着地震动激励峰值的提高，主梁加速度峰值增加幅度降低。

采用减震率r来体现隔震支座的减隔震作用，即

(12)

在不同抗震设防烈度地震作用下，隔震支座的减震率如表2所示。可知，顺桥向桥梁模型的最大减震率为92%，横桥向的最大减震率为86%。同时，输入地震动强度越大，高铁桥梁模型中隔震支座的减隔震效果越显著。

表2 隔震支座的减震率 %

3.3 位移响应分析

在不同抗震设防烈度地震作用下主梁、墩顶位移与支座剪切变形如表3所示。可知，桥梁模型墩顶和主梁位移、支座剪切变形均随地震动强度的增加而增加。2次地震作用下支座剪切变形存在一定差异，其中，El Centro地震波作用下支座的剪切变形较大。

9度(0.72g)地震作用下单个摩擦摆支座的滞回曲线如图11所示。可知，在不同抗震设防烈度地震作用下摩擦摆支座的滞回曲线稳定、饱满，具有良好的耗能性能。此外，由于地震动频谱特性的差异，虽然输入的2条地震动加速度峰值相同,但隔震支座的滞回耗能能力存在一定差异。

表3 主梁、墩顶位移与支座剪切变形 mm

图11 9度(0.72g)地震作用下单个摩擦摆支座的滞回曲线

3.4 应变响应分析

在不同抗震设防烈度地震作用下，桥墩混凝土和钢筋应变峰值如表4所示。可知，随着加速度峰值的增加，混凝土和钢筋的应变峰值均未显著增加。桥墩底部钢筋的应变峰值为53.33×10-6，混凝土材料应变峰值为58.14×10-6，均未达到钢筋和混凝土的屈服应变。在整个试验过程中，模型混凝土外表面未发现裂缝和破坏，结构基本处于弹性状态。

表4 桥墩混凝土和钢筋应变峰值(x向输入) 10-6

4 结论

本文通过水平低周反复加载试验和模拟地震振动台试验，研究一跨典型高铁简支梁桥的整体抗震性能，得到以下结论：

1)采用低周反复加载试验对隔震支座水平力-位移本构关系进行研究，发现理论值与试验值比较吻合，即采用双折线滞回模型能有效模拟双凹面摩擦摆支座的水平力-位移本构关系。

2)根据振动台试验和数据分析结果可知，隔震支座水平力-位移的滞回曲线饱满，强震作用下通过支座的滑移消耗了大量的地震能量，说明双凹面摩擦摆支座具有良好的耗能能力。

3)采用双凹面摩擦摆支座隔震后，主梁加速度相对于墩顶有较大幅度的减小，大大降低了高铁桥梁在地震作用下的破坏程度。随着地震动加速度峰值的增大，减震率有所提高。

4)在不同抗震设防烈度地震作用下，隔震桥梁模型中桥墩的钢筋和混凝土均未达到屈服和开裂应变，且在试验后也未发现任何裂缝，说明结构仍处于弹性状态。

[1]张骏,阎贵平.减隔震支座对梁式桥抗震性能的影响[J].中国公路学报,2002,15(1):38-43.

[2]韩强,杜修力,刘文光,等.不同地震烈度下隔震连续梁桥模型振动台试验[J].中国公路学报,2008,21(6):50-56.

[3]ZAYAS V A,LOW S S,MAHIN S A.A Simple Pendulum Technique for Achieving Seismic Isolation[J].Earthquake Spectra,2012,6(2):317-333.

[4]CONSTANTINOU M C,TSOPELAS P,KARTOUM A.Testing of Friction Pendulum Seismic Isolation Bearings for Bridges[C]//World Congress on Joint Sealants & Bearing Systems for Concrete Structures.California：World Congress on Joint Sealants and Bearing System for Concrete Structures，1997:613-632.

[5]MOKHA A,CONSTANTINOU M,REINHORN A.Teflon Bearings in Base Isolation I:Testing[J].Journal of Structural Engineering,1990,116(2):438-454.

[6]夏修身,赵会东,欧阳辉来.高速铁路桥梁基于摩擦摆支座的减隔震研究[J].工程抗震与加固改造,2014,36(3):21-26.

[7]PENG T B,YU X T,WANG Z N,et al.Study of the Seismic Performance of Expansion Double Spherical Seismic Isolation Bearing for Continuous Girder Bridges[J].Earthquake Engineering and Engineering Vibration,2012,11(2):163-172.

[8]WEI Z H,YUAN W C,CHEUNG P C,et al.Seismic Perfor-mance of Continuous Girder Bridges Using Cable-sliding Friction Aseismic Bearing[J].Procedia Engineering,2011,14:914-921.

[9]刘健新,胡兆同,李子青.桥梁结构减震设计方法研究[J].中国公路学报,2000,13(4):73-75,79.

[10]黄宇辰.FPS在高速铁路简支梁桥中的适用性研究[D].石家庄：石家庄铁道大学,2016.

[11]杨林,常永平,周锡元,等.FPS隔震体系振动台试验在高速铁路桥梁中的隔震性能研与有限元模型对比分析[J].建筑结构学报,2008,29(4):66-72.

[12]李冰,王少华,邓斌.摩擦摆支座究[J].机械科学与技术,2015,34(3):339-343.

[13]周颖,吕西林.建筑结构振动台模型试验方法与技术[M].北京:科学出版社，2012.