智能叶片风力机建模及多目标尾缘襟翼控制

张文广， 白雪剑

(1．华北电力大学 新能源电力系统国家重点实验室，北京 102206；2．华北电力大学 工业过程测控新技术与系统北京市重点实验室，北京 102206)

随着风力机的大型化发展，风力机叶片尺寸不断增大，从而加剧了其疲劳载荷和极限载荷。为了更好地应对大型风力机叶片的不利载荷波动，智能叶片的概念应运而生。其中，尾缘襟翼技术通过改变翼型形状来改变叶片气动性能，具有响应快速，调节能力强等特点，被认为是目前最为可行的主动降载智能叶片技术[1]。

国内外学者对带有尾缘襟翼的大型风力机智能叶片技术进行了研究。Hulskamp等[2]设计了一个直径为1.8 m的带有尾缘襟翼的风力机，并通过风洞实验验证了尾缘襟翼在降低叶片载荷方面的有效性。Castaignet等[3]在Vestas V27型风力机叶片上安装了70 cm长的尾缘襟翼，实验数据表明在1P频率处叶片根部载荷的幅值减少了20%。卢经纬等[4]提出了带有尾缘襟翼的风力机气动经验公式，并采用反步法设计了非线性控制器，仿真结果表明尾缘襟翼控制器可有效地稳定风力机输出功率。但对于带有尾缘襟翼的智能叶片风力机建模以及尾缘襟翼在主动降载和抑制功率波动的多目标控制，尚没有详细的研究。

因此，笔者基于NREL 5 MW参考风力机，在每个叶片上设计了2段独立的尾缘襟翼，采用Matlab/Simulink搭建了带有尾缘襟翼的智能叶片风力机模型，通过FAST气弹仿真平台对所建模型进行了对比验证，并在此基础上研究了多目标多襟翼控制器在主动降载和抑制功率波动方面的控制。

1 建模对象

以NREL 5 MW参考风力机为基础，在每个叶片上增加2段独立的尾缘襟翼，建立了带尾缘襟翼的智能叶片风力机模型。

1.1 风力机参数

NREL 5 MW参考风力机为三叶片变速变桨型风力机，其主要参数见表1[5]。

1.2 尾缘襟翼

NREL 5 MW参考风力机叶片总长61.5 m，由8种翼型组成[5]，使用文献[6]的最优尾缘襟翼参数，在每个叶片上增加2段独立的尾缘襟翼，襟翼1位于第23～25叶素段上，襟翼2位于第26～29叶素段上。带尾缘襟翼的叶片结构及襟翼1和襟翼2的位置如图1所示。

2 智能叶片风力机建模

所建立的智能叶片风力机模型主要分为气动模型、传动链模型以及双馈感应发电机模型。

表1 NREL 5 MW参考风力机参数

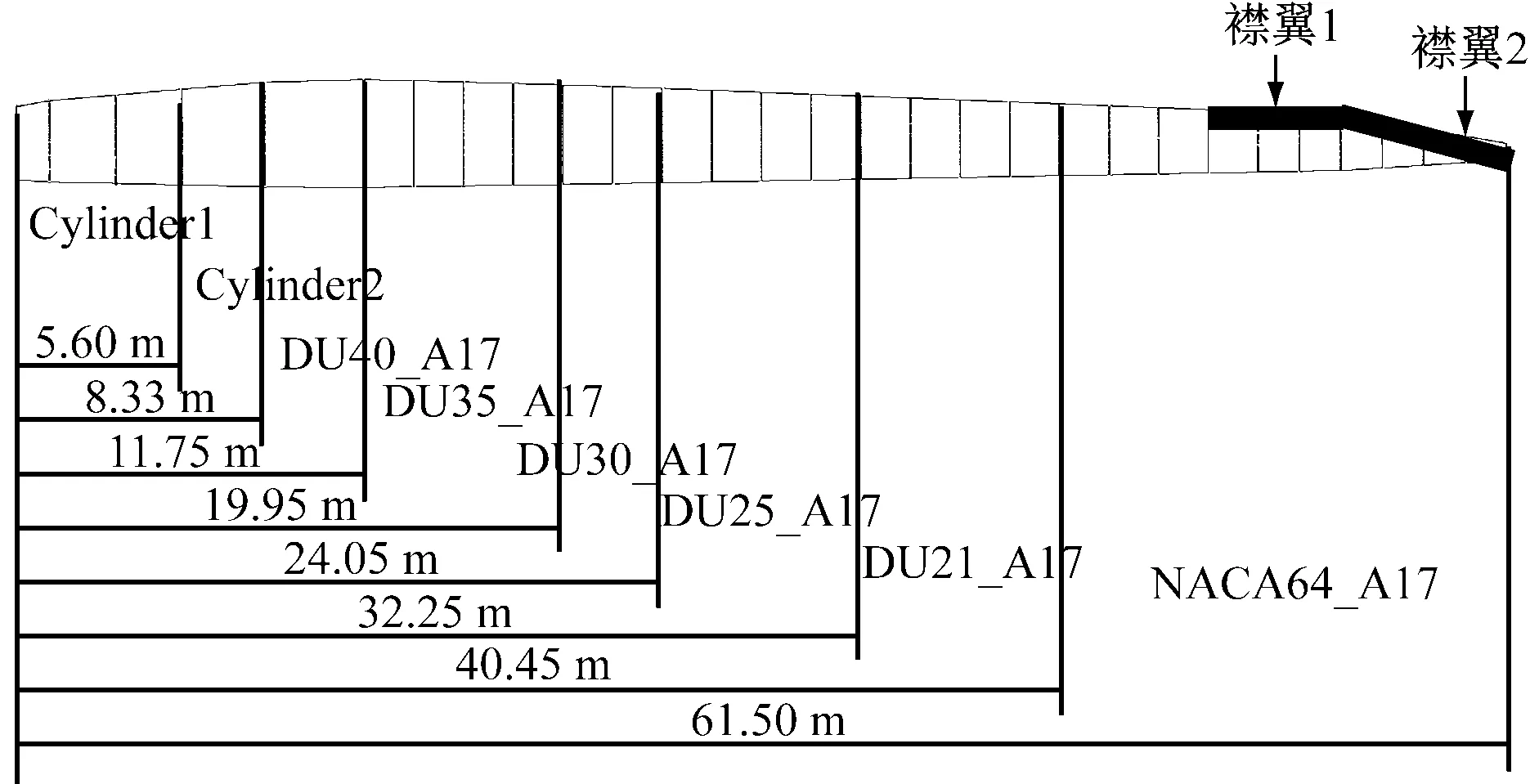
图1 带尾缘襟翼的NREL 5 MW参考风力机叶片结构图

2.1 气动模型

叶素动量理论是风力机空气动力学的经典计算方法，具有计算速度快、精度高的特点。本文的气动模型是在经典叶素动量理论基础上，增加了尾缘襟翼角输入量，并考虑叶尖损失修正和葛劳渥特修正，从而建立了带尾缘襟翼的智能叶片风力机气动模型。

2.1.1 叶素动量理论

叶素动量理论分为叶素理论和动量理论。叶素理论将叶片沿展向分为许多叶素，假设每个叶素上的空气动力学特性相互独立；动量理论是将包含风力机的环形控制体离散为多个环形单元控制体，假设控制体流体不可压缩且相互独立[7]。

叶素动量理论算法首先需要结合叶素与动量理论进行迭代计算，得出每个叶素上的局部载荷，迭代计算步骤如下。

(1)对轴向诱导因子a和切向诱导因子a′初始化，取a=a′=0。

(2)计算入流角φ：

(1)

式中：v0为入流风速；ω为叶轮转速；r为叶素局部半径。

(3)计算局部攻角α：

α=φ-θ

(2)

式中：θ为局部桨距角，θ=(θp+β)，其中θp为桨距角，β为叶素扭角。

(4)采用线性插值法从翼型数据表中求得升力系数Cl(α)和阻力系数Cd(α)。

(5)计算法向力系数Cn和切向力系数Ct：

Cn=Clcosφ+Cdsinφ

(3)

Ct=Clsinφ-Cdcosφ

(4)

(6)引入普朗特叶尖损失因子F，计算轴向诱导因子a和切向诱导因子a′：

(5)

(6)

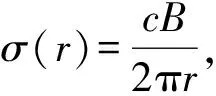
(7)引入a值较大的葛劳渥特修正：

(7)

式中：CT为推力系数。

(8)判断a与a′的变化值是否大于0.01，若大于0.01，返回第(2)步，否则计算完成。

叶素局部法向载荷pN和局部切向载荷pT计算式如下：

(8)

(9)

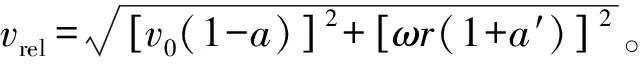
则叶片上的切向力矩MT和法向力矩MN分别为：

(10)

(11)

由式(10)和式(11)可得叶轮转矩Mr、叶轮功率PAero、功率系数Cp和叶片挥舞方向弯矩Mflap为：

(12)

PAero=Mr·ω

(13)

(14)

Mflap=MNcosθp-MTsinθp

(15)

2.1.2 尾缘襟翼角的引入

对于所设计的带尾缘襟翼的翼型，升力系数Cl和阻力系数Cd随着攻角α和襟翼角γ的变化而变化。

采用Xfoil软件[8]，在NACA64_A17翼型的基础上，改变尾缘偏转角，得到不同尾缘襟翼角γ的翼型，并对翼型进行气动分析计算，得到上述尾缘襟翼翼型的升力系数Cl和阻力系数Cd随攻角α变化的数据表。整理后得到Cl(α,γ)和Cd(α,γ)的二维数据表，则不同攻角α和襟翼角γ下的Cl(α,γ)和Cd(α,γ)可以通过线性插值法查表得到。

2.2 传动链模型

风力机的传动系统可以看成是由有限个惯性单元、弹性单元和阻尼单元组成的。因此，在建立传动链模型时，可以采用弹簧-阻尼-质量系统作为动力学模型[9]。通过有选择地考虑传动轴的柔性和旋转部分的惯量，将传动链模型分为单质块模型、双质块模型和三质块模型[10]。

与风轮转子和发电机的转动惯量相比，齿轮箱的转动惯量很小，笔者参考FAST气弹仿真平台[11]，传动链模型采用双质块模型，忽略了齿轮箱转动惯量，考虑了低速轴的柔性和阻尼特性，并视高速轴为刚性。

根据图2，风轮转子和低速轴的运动方程：

(16)

(17)

齿轮箱的运动方程：

TL=N·TH

(18)

θL=θH/N

(19)

高速轴和发电机的运动方程：

θH=θG

(20)

(21)

式中：Jr为风轮转子转动惯量；JG为发电机转动惯量；θr为风轮转子角位移；θL为低速轴角位移；θH为高速轴角位移；θG为发电机角位移；Tr为风轮转子气动扭矩；TL为低速轴扭矩；TH为高速轴扭矩；TG为发电机的电磁转矩；K为低速轴刚度；C为低速轴阻尼；N为齿轮箱传动比。

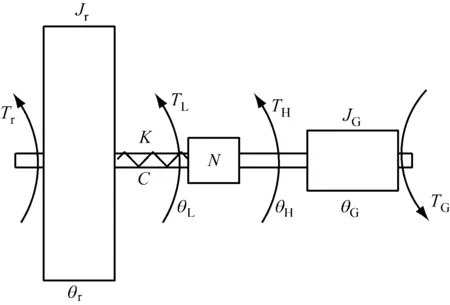
图2 双质块传动链模型等效图

2.3 双馈感应发电机模型

双馈感应发电机又称转子交流励磁电机，主要包括电机本体和交流励磁及控制系统2部分。所使用的双馈感应发电机是在Simulink中双馈异步发电机的基础上，通过修改其内部结构[12]和发电机参数[13]，并调整其矢量控制的控制器参数，得到额定功率为5 MW的双馈感应发电机模型(见图3)。

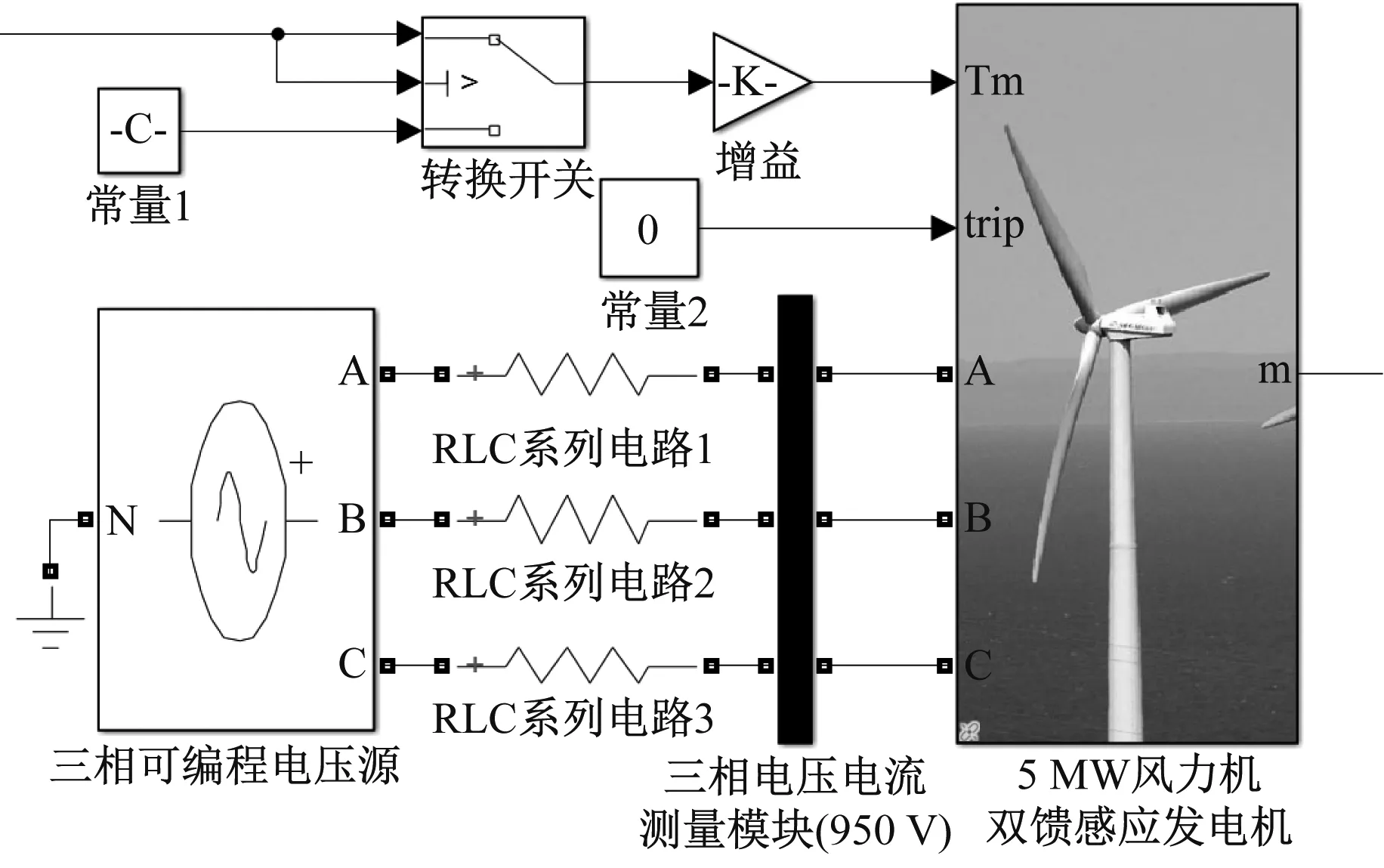
图3 5 MW风力机双馈感应发电机模型

3 智能叶片风力机模型验证

FAST是由NREL开发的气弹仿真平台，可计算两叶片或三叶片水平轴风力机的极端载荷和疲劳载荷[14]，其经过GL认证，计算结果准确度高。针对无襟翼和有襟翼的情况，采用基于FAST的带尾缘襟翼的风力机气弹仿真平台[6]对所建立的智能叶片风力机模型进行对比验证。

3.1 4～11 m/s阶跃变化风况对比

仿真时间为800 s，仿真风况为每100 s增加1 m/s的阶跃变化风况，变化范围为4～11 m/s。图4给出了轮毂高度风速从4 m/s到11 m/s阶跃增加时，智能叶片风力机模型与FAST气弹仿真平台的对比图。从图4可以看出，与FAST气弹仿真平台相比，智能叶片风力机模型叶片1叶根挥舞弯矩偏差小于4.6%，发电机转速偏差小于0.2%，发电机功率偏差小于0.5%。可见，在4～11 m/s的阶跃变化风况下，所建立的智能叶片风力机模型精度较高。

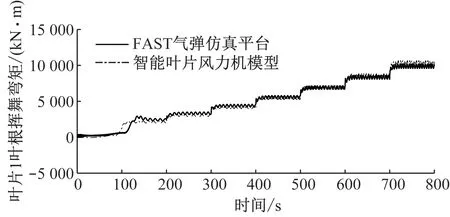
(a)叶片1叶根挥舞弯矩

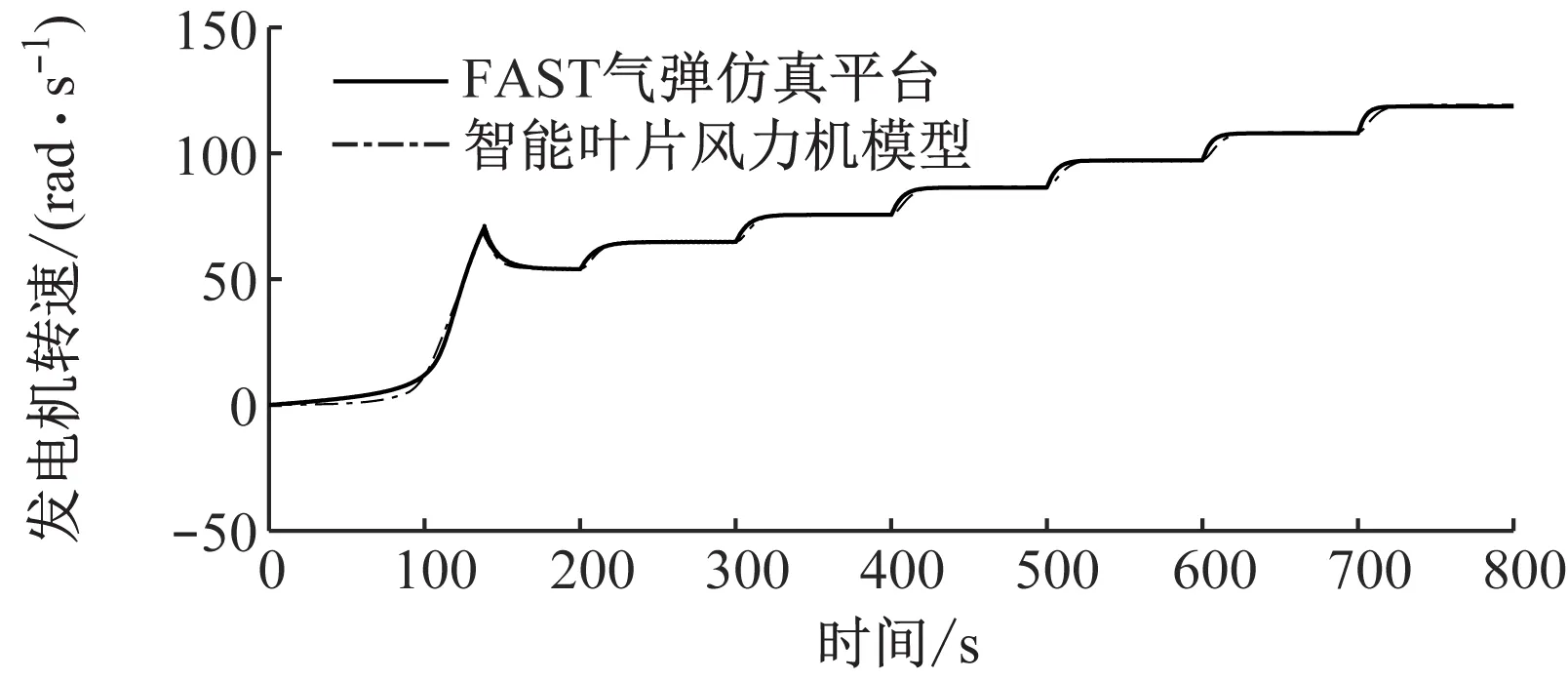
(b)发电机转速

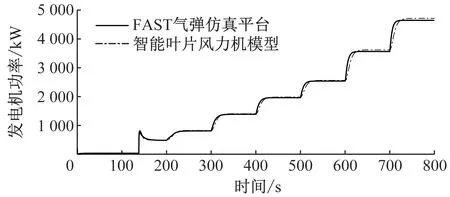
(c)输出功率

3.2 11～24 m/s阶跃变化风况对比

仿真时间为1 400 s，仿真风况为每100 s增加1 m/s的阶跃变化风况，变化范围为11～24 m/s。图5给出了轮毂高度风速从11 m/s到24 m/s阶跃增加时，智能叶片风力机模型与FAST气弹仿真平台的对比图。从图5可以看出，与FAST气弹仿真平台相比，智能叶片风力机模型叶片1叶根挥舞弯矩偏差小于9.4%，变桨角偏差小于0.8%，发电机转速偏差小于0.2%，发电机功率偏差小于1.5%。可见，在11～24 m/s阶跃变化风况下，所建立的智能叶片风力机模型精度较高。

3.3 平均风速为11.4 m/s时标准湍流风况对比

仿真时间为300 s，仿真风况为轮毂高度平均风速为11.4 m/s，湍流强度为5%的标准湍流风况。

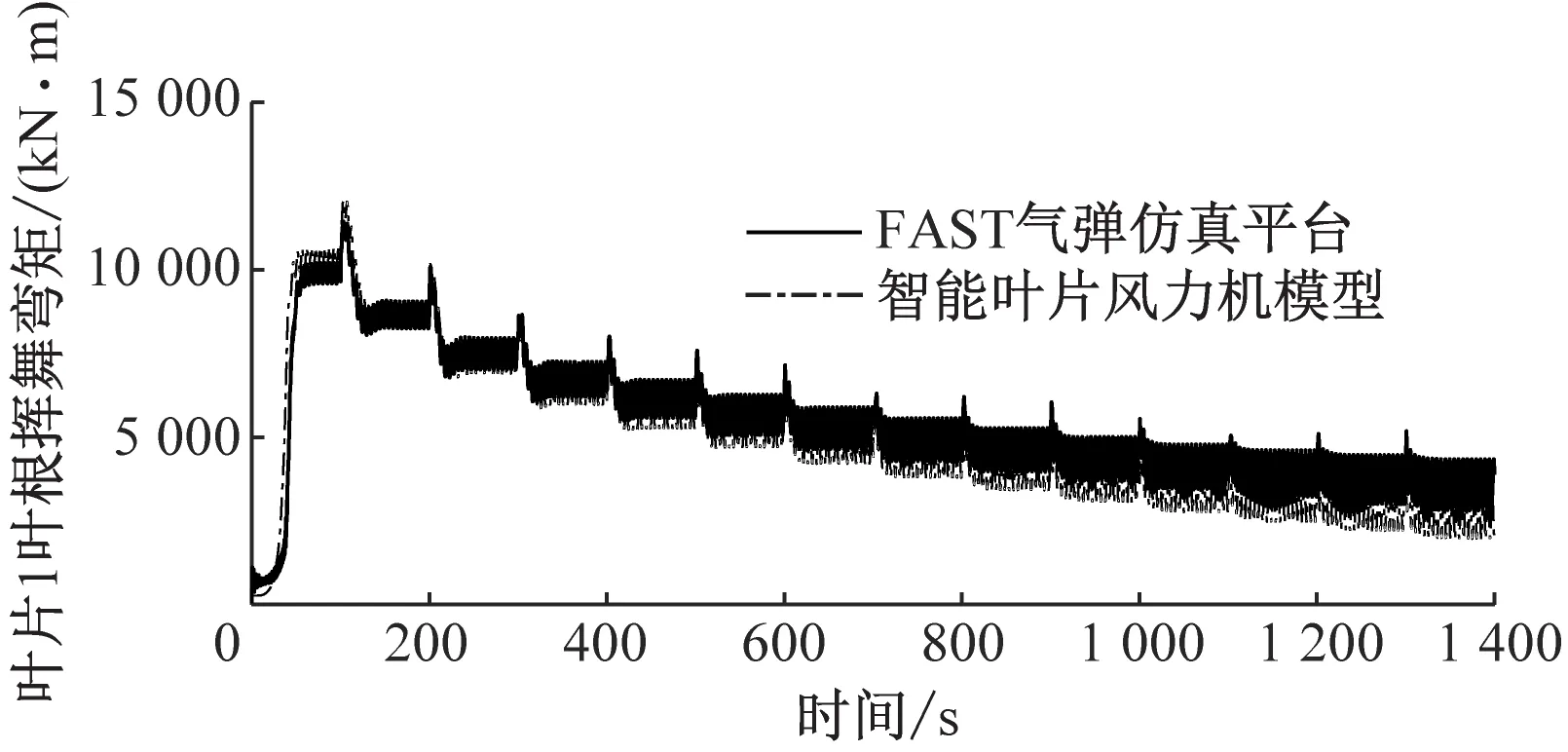
(a)叶片1叶根挥舞弯矩

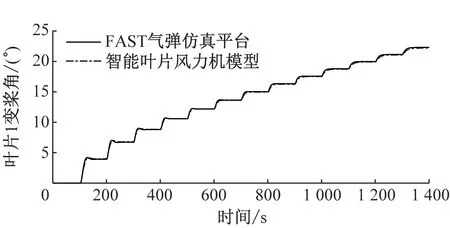
(b)叶片1变桨角

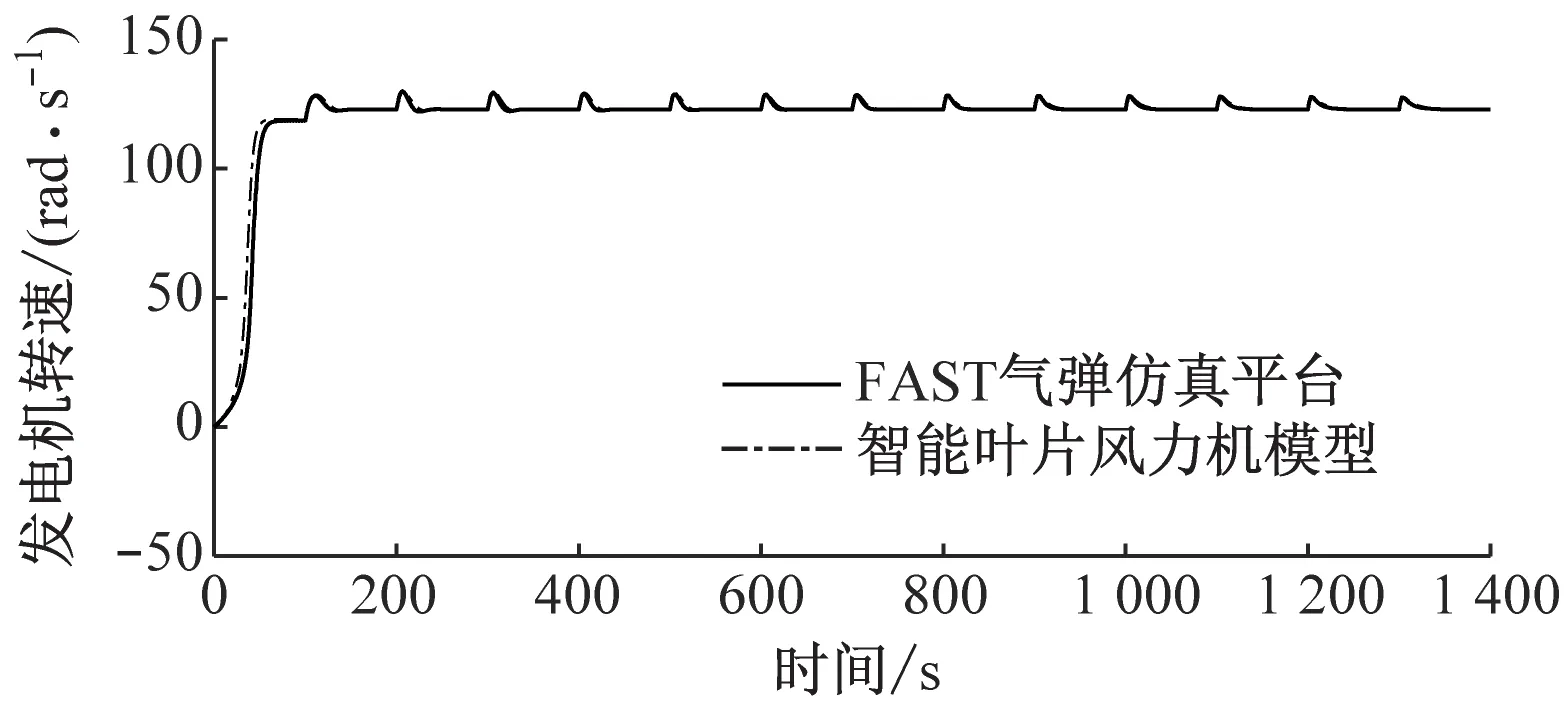
(c)发电机转速

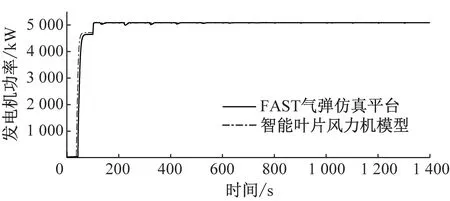
(d)发电机输出功率

图6给出了轮毂高度平均风速为11.4 m/s的标准湍流风况下，智能叶片风力机模型与FAST气弹仿真平台的对比图。从图6可以看出，与FAST气弹仿真平台相比，智能叶片风力机模型叶片1叶根挥舞弯矩偏差小于2.4%，变桨角偏差小于3.4%，发电机转速偏差小于0.3%，发电机功率偏差小于0.3%。因此，在标准湍流风况下，所建立的智能叶片风力机模型精度较高。

3.4 15 m/s稳定风况下变桨及襟翼控制对比

仿真时间为200 s，仿真风况为轮毂高度风速为15 m/s的稳定风况。对每个叶片上的2个襟翼采用相同的独立襟翼控制方法[15]。

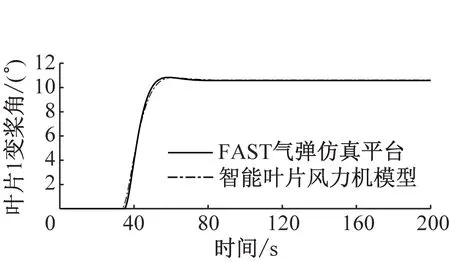
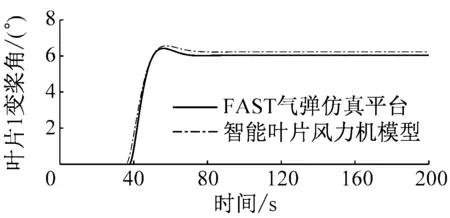
图7给出了轮毂高度风速为15 m/s的稳定风况下，智能叶片风力机模型与FAST气弹仿真平台的对比图。从图7可以看出，智能叶片风力机模型与FAST气弹仿真平台相比，无襟翼控制时，叶片1叶根挥舞弯矩偏差小于7.3%，变桨角偏差小于0.4%；有襟翼控制时，叶片1叶根挥舞弯矩偏差小于9.2%，变桨角偏差小于3.1%，襟翼角在100～200 s的平均偏差小于0.1%。因此，在变桨及襟翼控制方面，智能叶片风力机模型精度较高。对比图7(a)～图7(d)可以看出，有襟翼控制时，叶片1的叶根挥舞弯矩波动幅度明显减小，其变桨角也明显减小。

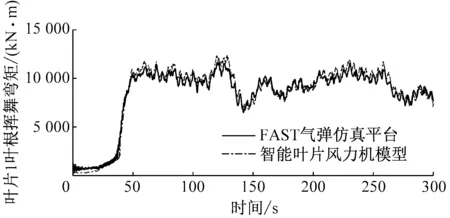
(a)叶片1叶根挥舞弯矩

(b)叶片1变桨角

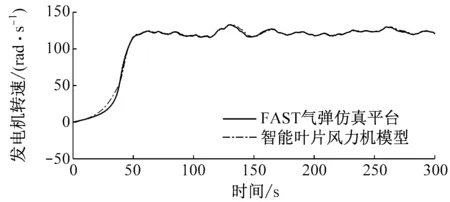
(c)发电机转速

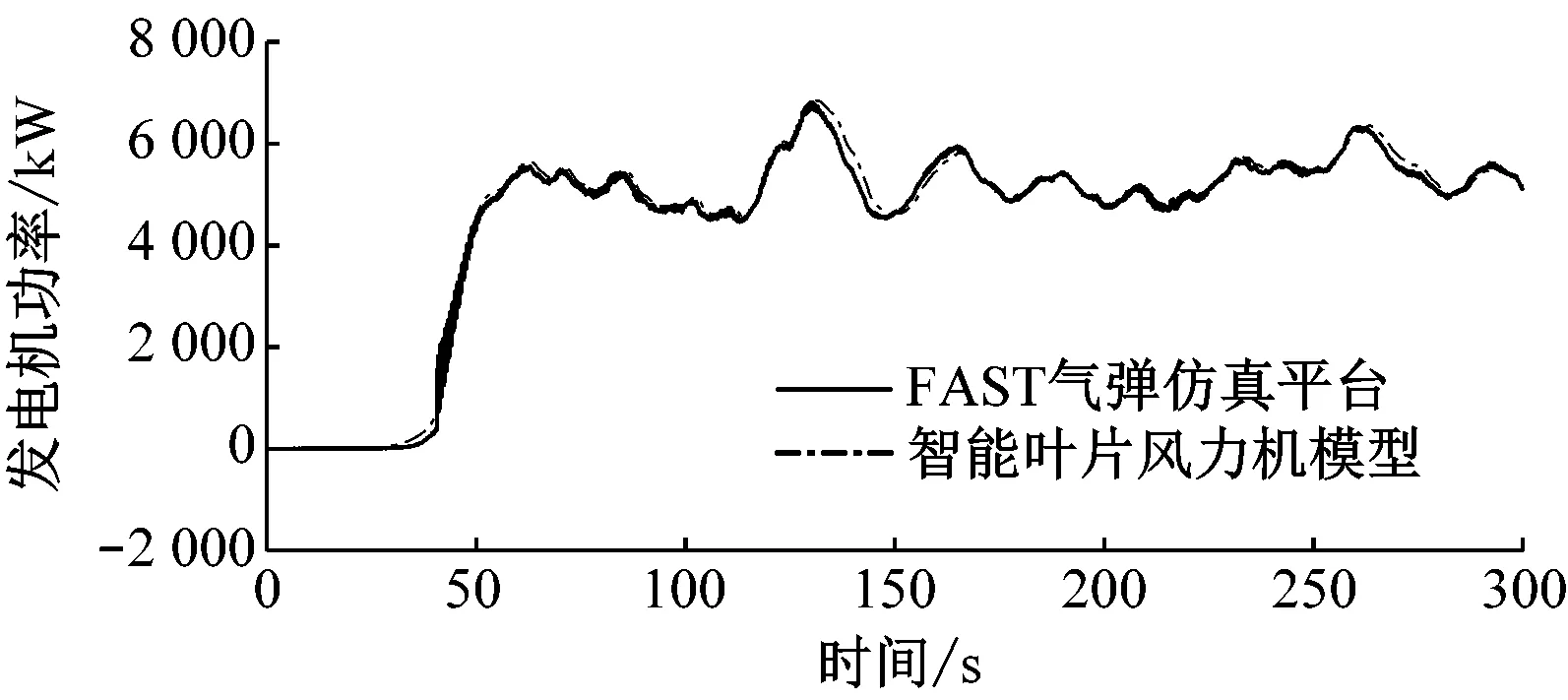
(d)发电机输出功率

从以上4种风况的对比情况可以看出，与FAST气弹仿真平台相比，智能叶片风力机模型在整个风力机工作范围的稳定风况以及湍流风况下，叶片1的叶根挥舞弯矩偏差小于9.4%，发电机转速偏差小于0.3%，发电机功率偏差小于1.5%，叶片1的变桨角偏差小于3.4%，叶片1的襟翼角偏差小于0.1%。说明所建立的智能叶片风力机模型对风力发电过程的仿真具有较高精度，计算结果具有较高的可信性。

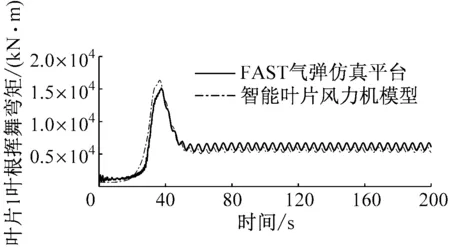
(a)无襟翼控制时叶片1叶根挥舞弯矩

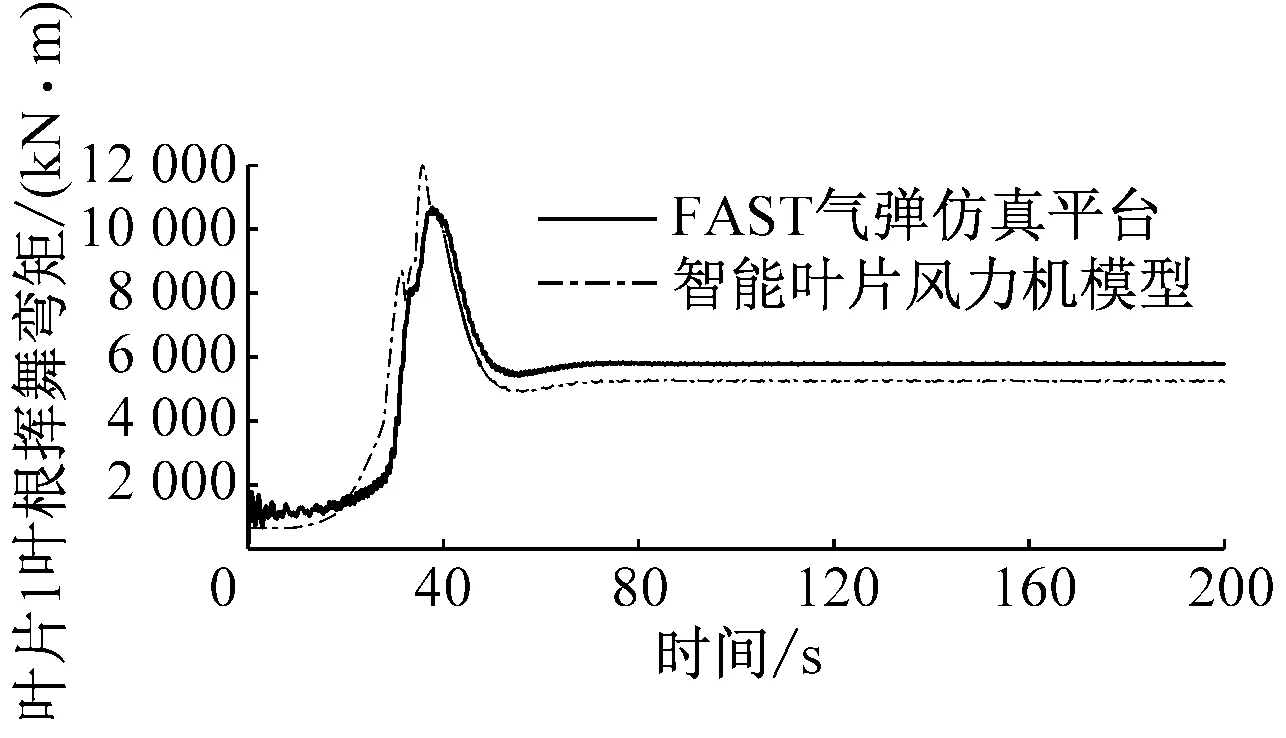
(b)有襟翼控制时叶片1叶根挥舞弯矩

(c)无襟翼控制时叶片1变桨角

(d)有襟翼控制时叶片1变桨角

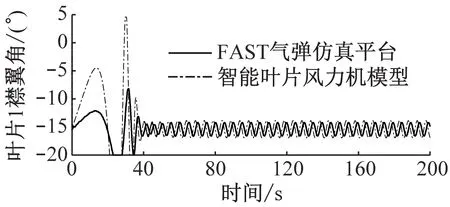
(e)有襟翼控制时叶片1襟翼角

4 多目标的多襟翼控制

更靠近叶尖的尾缘襟翼能更有效地减少叶根载荷，对功率的影响也更小[16]。为了更好地发挥尾缘襟翼在降载及抑制功率波动方面的作用，采用图1所示的襟翼1控制发电机的功率波动，襟翼2控制叶根挥舞弯矩。

襟翼1采用PID方法(PID1)来控制襟翼偏转角，从而抑制发电机功率产生的波动；襟翼2采用PID方法(PID2)来控制襟翼角的周期性变化，以减少叶根挥舞弯矩产生的周期性波动。因此，襟翼1和襟翼2控制器之间耦合作用较弱，可忽略相互间的影响。PID1的反馈信号为发电机转速，设定值为当前控制时刻前20 s的发电机转速平均值；PID2采用独立襟翼控制器[15]，反馈信号为叶根挥舞弯矩的偏航和俯仰分量，设定值为0。

在轮毂高度平均风速为11.4 m/s的湍流风况下进行仿真，在80 s加入襟翼2控制，100 s加入襟翼1控制，并与无襟翼的仿真结果进行对比，选取第150～250 s的数据进行分析，结果见表2。叶片1叶根挥舞弯矩标准差、叶片1叶根挥舞弯矩1P处功率谱密度、发电机转速标准差和发电机功率标准差的变化率分别为-18.26%、-89.73%、-74.65%和-75.07%。

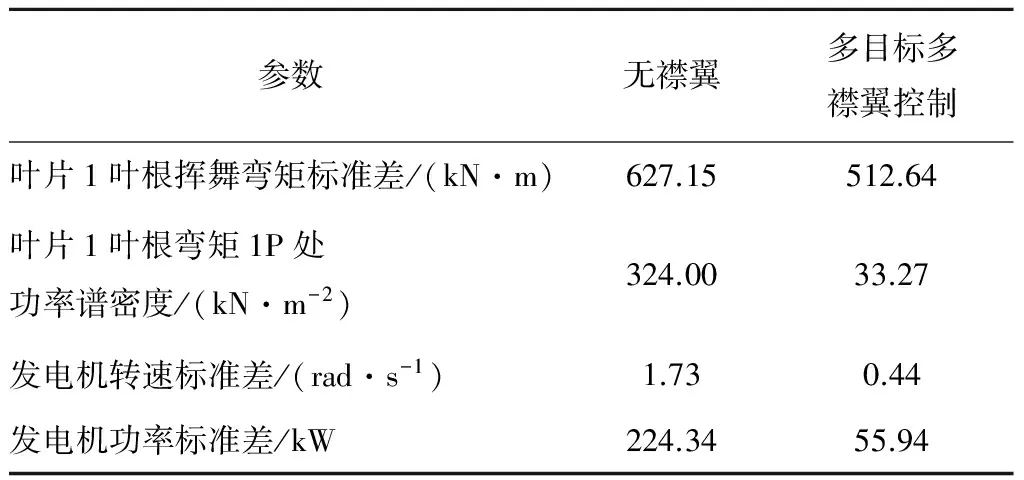
表2 标准湍流风况下有无襟翼控制的风力机参数对比

图8给出了标准湍流风况叶片1叶根挥舞弯矩及其功率谱密度。由图8可知，多目标多襟翼控制下，叶根挥舞弯矩的振荡明显减弱，特别是在1P频率，即0.2 Hz处，叶根挥舞弯矩的功率谱密度有明显降低。其标准偏差减少了18.26%，1P频率处的功率谱密度减少了89.73%。说明在标准湍流风况下，多目标多襟翼控制可有效降低叶片的疲劳载荷。

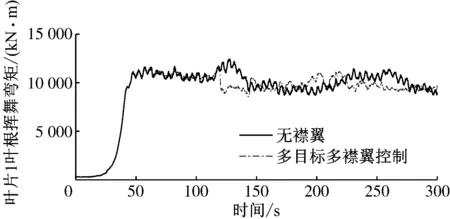
(a)叶片1叶根挥舞弯矩

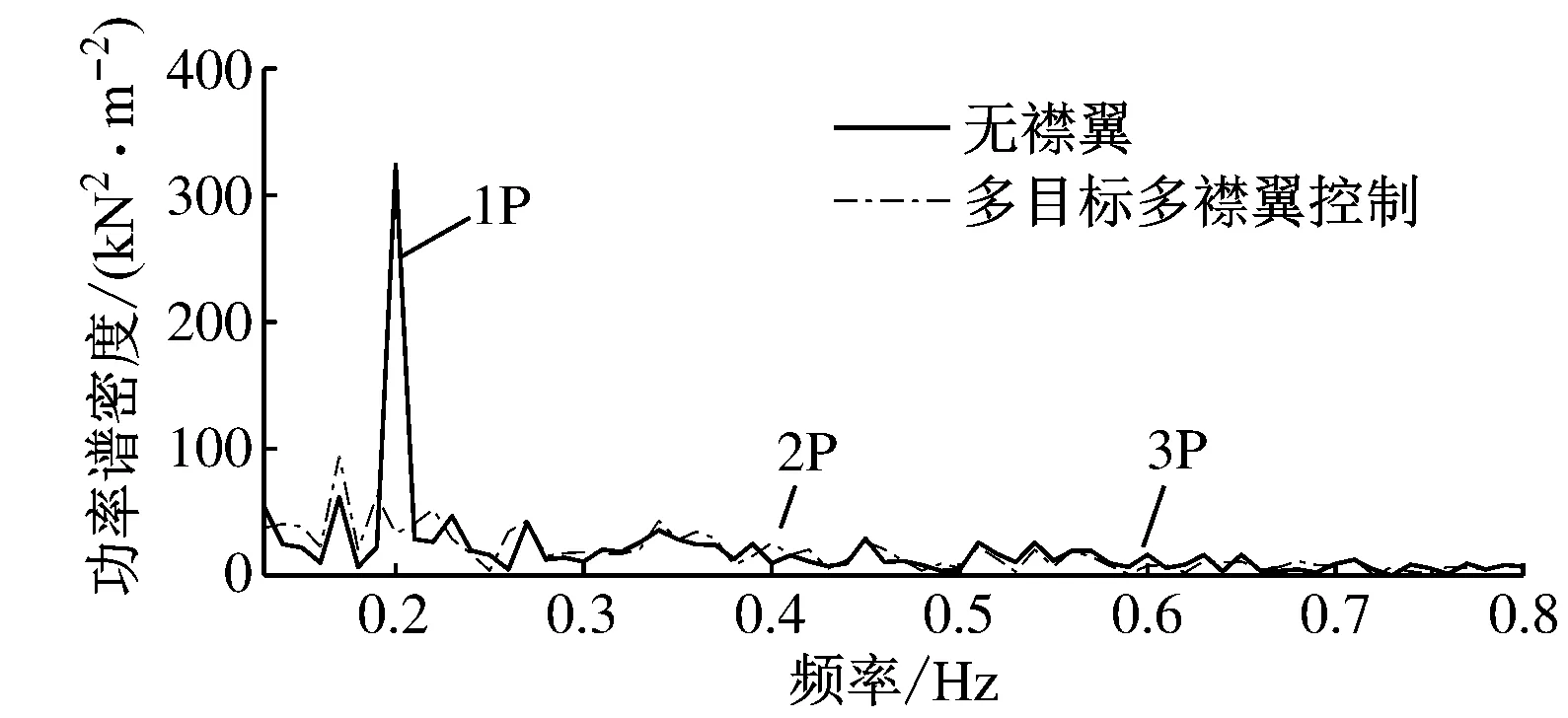
(b)叶片1叶根挥舞弯矩的功率谱密度

图9和图10分别为标准湍流风况下风力机的发电机转速和高速轴功率。由图9、图10可知，在多目标多襟翼控制作用下，风力机发电机转速和发电机功率波动明显减小，其标准偏差分别减少74.65%和75.07%。说明多目标多襟翼控制使风力机功率输出更平滑，从而使风电场的出力更平稳，更利于电网接纳风电。

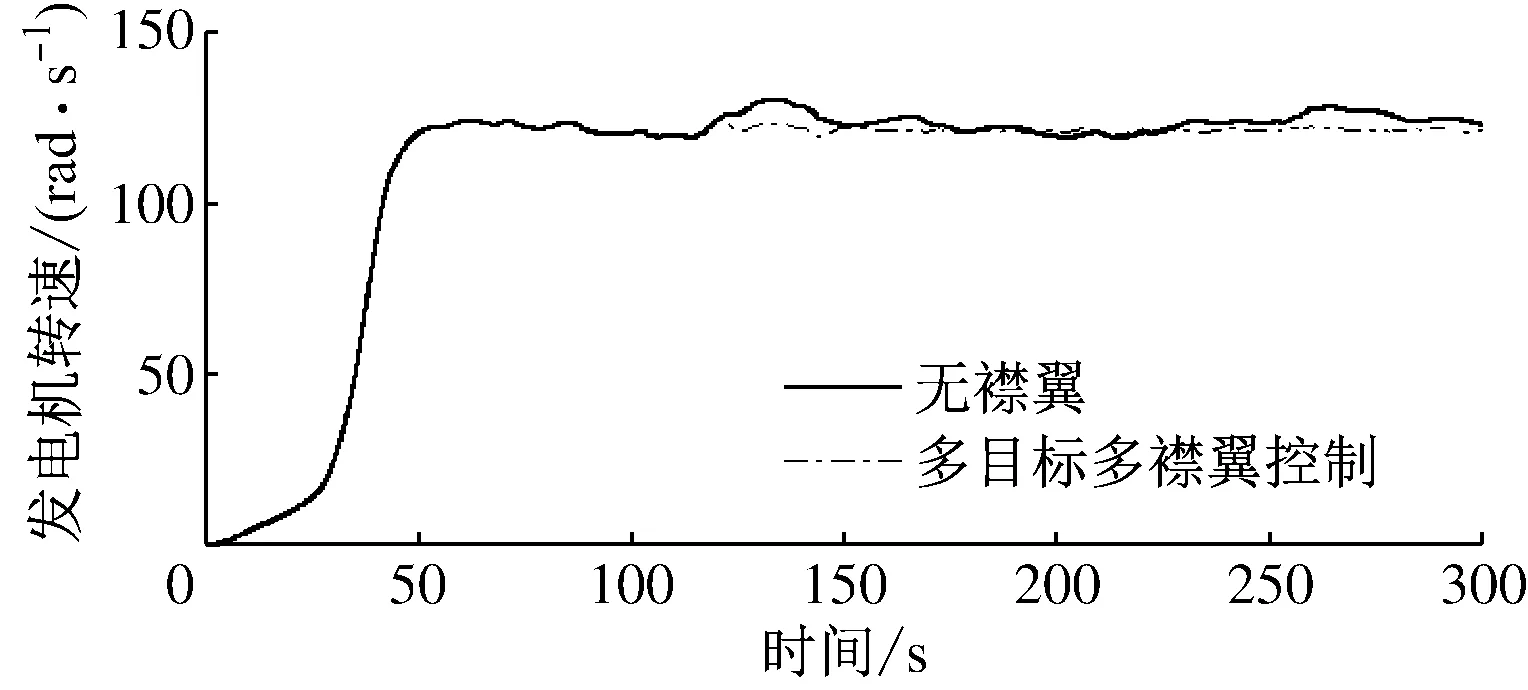
图9 标准湍流风况风力机发电机转速

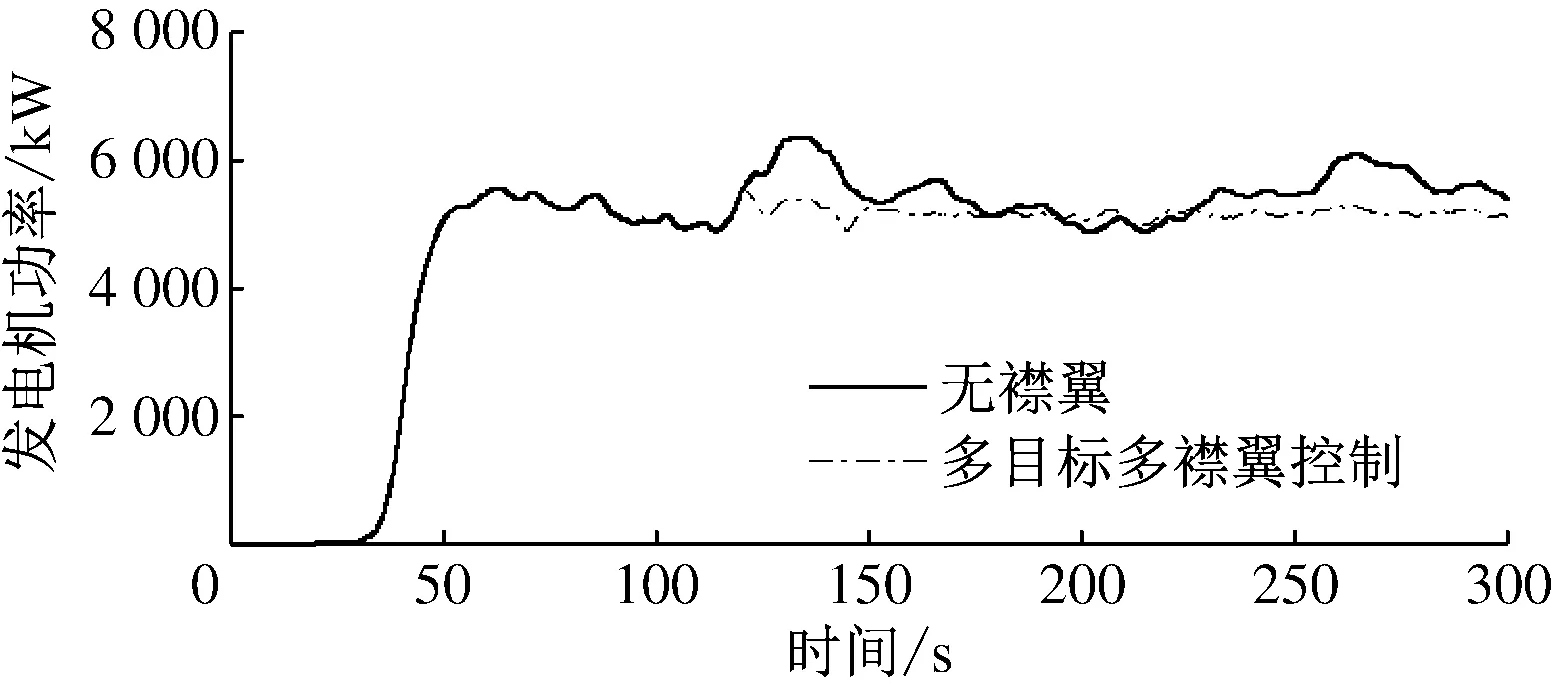
图10 标准湍流风况风力机高速轴功率

图11给出了标准湍流风况下叶片1的襟翼角。由图11可知，在多目标多襟翼控制作用下，襟翼2在PID2作用下进行周期性摆动控制，几乎不受襟翼1的PID1控制影响。这也说明了2个襟翼控制器之间耦合关系较弱，可独立进行控制。

图11 标准湍流风况叶片1的襟翼角

5 结 论

(1)在整个风力机工作范围内稳定风况以及轮毂平均风速为11.4 m/s的标准湍流风况下，将所建立的智能叶片风力机模型叶片1的叶根挥舞弯矩、变桨角和襟翼角以及发电机转速、发电机功率这5个参数与FAST气弹仿真平台中的相应参数进行对比，结果表明所建立的智能叶片风力机模型对风力机发电过程的仿真精度较高，计算结果具有一定的可信度。

(2)在标准湍流风况下，多目标多襟翼控制不仅可以大幅减小叶根挥舞弯矩在1P频率处的幅值，而且可以有效减弱发电机转速的波动，平滑风力机输出功率。这说明多目标多襟翼控制不仅可以显著降低叶片的疲劳载荷，延长风力机寿命，而且可以抑制风力机输出功率波动，显著改善智能叶片风力机并网对电网的影响，具有一定的实际参考价值。

参考文献：

[1] COUCHMAN I, CASTAIGNET D, POULSEN N K, et al. Active load reduction by means of trailing edge flaps on a wind turbine blade[C]//Proceedingsof2014AmericanControlConference. Portland, USA: IEEE, 2014: 3722-3727.

[2] HULSKAMP A W, van WINGERDEN J W, BARLAS T, et al. Design of a scaled wind turbine with a smart rotor for dynamic load control experiments[J].WindEnergy, 2011, 14(3): 339-354.

[3] CASTAIGNET D, BARLAS T, BUHL T, et al. Full-scale test of trailing edge flaps on a Vestas V27 wind turbine: Active load reduction and system identification[J].WindEnergy, 2014, 17(4): 549-564.

[4] 卢经纬, 张臻, 梁宇坤, 等. 具有尾缘襟翼风力机的恒功率反步法控制[J].控制理论与应用, 2017, 34(1): 61-68.

LU Jingwei, ZHANG Zhen, LIANG Yukun, et al. Backstepping control of constant power for wind turbines with trailing edge flaps[J].ControlTheory&Applications, 2017, 34(1): 61-68.

[5] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Colorado: National Renewable Energy Laboratory, 2009.

[6] 张文广, 白雪剑, 韩越. 风力机尾缘襟翼结构参数优化及控制性能分析[J].动力工程学报, 2017, 37(12): 1023-1030.

ZHANG Wenguang, BAI Xuejian, HAN Yue. Trailing edge flap structure parameters optimization of a wind turbine and analysis of the control performance[J].JournalofChineseSocietyofPowerEngineering, 2017, 37(12): 1023-1030.

[7] HANSEN M O L. Aerodynamics of wind turbines[M]. 2nd ed. Oxford, UK: Earthscan, 2008: 45-57.

[8] DRELA M, YOUNGREN H. XFOIL 6.9 user primer[EB/OL]. [2016-11-01]. http://web.mit.edu/drela/Public/web/xfoil/xfoil_doc.txt.

[9] 刘豹. 风力发电机传动装置建模分析[D]. 沈阳: 东北大学, 2012.

[10] 刘吉臻. 新能源电力系统建模与控制[M]. 北京: 科学出版社, 2015.

[11] JONKMAN B, JONKMAN J. Resistant moment of the rotor and of the electric generator[EB/OL]. [2017-01-10]. https://wind.nrel.gov/forum/wind/viewtopic.php?f=2&t=525.

[12] SINGH M, MULJADI E, JONKMAN J, et al. Simulation for wind turbine generators-with FAST and MATLAB-Simulink modules[R]. USA: NREL, 2014.

[13] WU Bin, LANG Yongqiang, ZARGARI N, et al. Power conversion and control of wind energy systems[M]. Hoboken,USA: Wiley-IEEE Press, 2011.

[14] JONKMAN J M, BUHL JR M L. FAST user's guide-updated august 2005[R]. USA: NREL, 2005.

[15] AQUINO B B. New generator control algorithms for smart-bladed wind turbines to improve power capture in below rated conditions[D]. Amherst,USA: University of Massachusetts-Amherst, 2014.

[16] 张文广, 李腾飞, 刘吉臻, 等. 尾缘襟翼结构参数对大型风机气动性能影响的仿真研究[J].可再生能源, 2016, 34(12): 1826-1833.

ZHANG Wenguang, LI Tengfei, LIU Jizhen, et al. Simulation study on trailing edge flaps' structure parameters affecting aerodynamic performance of large wind turbines[J].RenewableEnergyResources, 2016, 34(12): 1826-1833.