一种改进型LSSVM模型在电站锅炉燃烧与优化中的应用

李应保， 王东风

(1． 华北电力大学 自动化系， 河北保定 071003；2． 华北电力大学 河北省发电过程仿真与优化控制工程技术研究中心， 河北保定 071003)

电站锅炉内煤粉的燃烧与热量传递是一个复杂的物理化学过程[1]，受到诸多因素的影响，如锅炉内的含氧量、各台给煤机的给煤量、各个送风出口的开度、煤种特性、煤粉细度以及锅炉的负荷、主蒸汽压力和温度等运行参数也会间接影响锅炉的燃烧状态。要建立锅炉内煤粉多相燃烧和流体力学的数学机理模型往往很困难[2]，即使通过各种辨识的方法建立了锅炉燃烧参数的传递函数模型或差分方程模型，也不能保证模型的实时有效性和准确性，基于机器学习的建模方法很好地克服了复杂系统建模的难题，并被成功应用于电站锅炉实时在线燃烧参数的预测，为指导锅炉燃烧优化提供了基础。

王禹朋等[3]运用支持向量机算法建立了某亚临界300 MW机组烟煤锅炉的煤耗率和NOx生成量的预测模型；余廷芳等[4]利用BP神经网络建立了锅炉燃烧特性的模型，预测了锅炉热效率和NOx的质量浓度，并结合遗传算法对锅炉燃烧多目标优化问题进行了优化；高芳等[5]对标准最小二乘支持向量机回归方法进行改进，建立了以锅炉热效率和NOx排放浓度为输出的共享最小二乘支持向量机模型，并采用粒子群算法对该模型中的锅炉运行工况进行了寻优。由此可见，针对锅炉燃烧系统的机器学习建模问题，大多数学者采用神经网络模型和最小二乘支持向量机预测模型(RCV-LSSVM)，并积极开展了模型改进方面的研究。

针对传统单一元素验证的最小二乘支持向量机(LSSVM)模型鲁棒性较差，预测精度较低等问题，在之前研究的基础上，笔者利用交叉验证概率计算的方法改进了传统LSSVM模型的风险评估机制，并用国内某350 MW机组锅炉燃烧系统的历史运行数据进行训练建模，对比了改进型LSSVM模型(即RCV-LSSVM)与传统LSSVM模型对锅炉排烟温度、尾部烟气中氧气体积分数、飞灰含碳量和NOx质量浓度的预测效果。最后根据多目标优化的综合经济指标函数，采用智能优化算法寻得最佳的锅炉燃烧输入参数，为锅炉的燃烧优化提供了重要的参考指标。

1 研究对象

研究对象为一台350 MW机组，亚临界、中间一次再热、强制循环Π型锅炉，炉膛尺寸为19.5 m×22.7 m，水冷壁为下螺旋管圈加上垂直管束，燃烧方式为四角切圆燃烧，如图1(a)所示。该锅炉配置了5台直吹式中速磨煤机，每个角上5层一次风喷口、各二次风门及燃尽风门的布置如图1(b)所示。从图1(b)可以看出，在每个一次风喷口周围都设有周界二次风，也称为燃料风，其作用是使一次风煤粉气流与少部分空气提前混合，有利于煤粉气流的着火；另外，辅助二次风喷口与一次风喷口相间布置，有利于携带大量氧化剂的空气与煤粉继续混合，从而保证煤粉充分燃烧；在一、二次风喷口上方还布置了2层燃尽风喷口，其目的是实现未燃物质的燃尽并协助二次风实现炉内脱硝，降低了NOx的生成量。

(a)四角切圆燃烧方式(b)角1燃烧器喷口和风门布置

图1 锅炉燃烧系统示意图

Fig.1 Schematic diagram of the boiler combustion system

2 数学模型

2.1 鲁棒交叉验证LSSVM理论

最小二乘支持向量机是在原始支持向量机算法的基础上对结构风险最小化函数进行改进，将二次规划优化问题转变为求解线性方程组的过程[6]。最小二乘支持向量机将优化问题描述为结构风险最小化函数R，并将约束条件转换为等式约束关系。

s.t.yi=ωT·φ(xi)+b+ei,i=1,2,…,n

(1)

式中：ω和b为决策函数的参数；正则化参数γ=c·vi，vi为正则化参数的权重因子，c为正则化参数常量；ei为误差向量；φ(xi)为核函数；yi为高维空间函数值。

将优化问题转化为拉格朗日函数表达式：

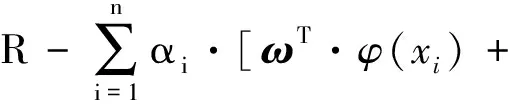
b+ei-yi]

(2)

式中：αi为拉格朗日乘子。

根据求解极值的库恩塔克条件(即K-T条件)，可以得到一组参数关系式：

(3)

式(3)用线性方程组可表达为：

(4)

式中：K(xi,xj)为最小二乘支持向量机的核函数，一般采用径向基函数(RBF)作为核函数；i，j=1,2,…,n；Dγ=diag(1/γ1,1/γ2,…,1/γn);I为单位矩阵；Y为非线性映射函数。

交叉验证(CV)是用来验证机器学习模型泛化能力的一种统计分析方法，在训练支持向量机模型时，交叉验证用来调整模型的参数，如正则化参数γ和核函数参数σ。假设样本集zi=(xi,yi)的大部分数据符合独立随机分布函数F(z)，损失函数L(z,FN(z))是偏差ek的二范数形式，鲁棒交叉验证将原始数据分成S组不相交的子集，每组数据个数为m，由此可定义一个鲁棒交叉验证评估函数[7]：

(5)

式中：F(N-m)(z)为N-m个组外F(z)的经验估计值；Fm(z)为m个组内F(z)的经验估计值；θ为支持向量机的超参数，即学习之前设置的参数，如模型训练层数、学习模式和学习率等参数。

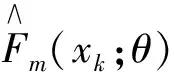
(6)

利用式(6)对每一组数据交替进行验证，其余的S-1组数据作为训练集，统计学实验证明交叉验证比单一元素验证的鲁棒性强，有效避免了机器学习模型过学习及欠学习现象的发生。

2.2 锅炉综合优化目标的设计

随着电厂对控制污染排放和锅炉设备保护意识的提高，电站锅炉燃烧优化已不再是提高锅炉效率的单一优化目标，而是一种集合了提高锅炉效率、降低排放和延长设备使用寿命等多个优化目标的综合经济指标[8]。但是各个目标之间存在一定的矛盾，如提高锅炉效率需要提高锅炉内的整体温度，过高温度势必会升高炉膛内NOx生成量，加重水冷壁和过热器管束的煤灰结渣程度并加速管道的腐蚀[9]。在工业实际生产过程中，一般用反平衡法估算锅炉效率：

η=100%-(LQ1+LQ2+LQ3+LQ4+LQ5)

(7)

式中：LQ1为排烟热损失；LQ2为机械不完全燃烧热损失；LQ3为可燃气体不完全燃烧热损失；LQ4为锅炉散热损失；LQ5为其他热损失。

在众多的热损失中，排烟热损失所占的比例最大，其次是机械不完全燃烧热损失和可燃气体不完全燃烧热损失。因此，表征排烟热损失的空气预热器出口烟温是一个非常重要的参数，烟气中的飞灰含碳量和氧气体积分数是不完全燃烧热损失的重要指标。

随着严格的污染排放标准[10]和严厉的污染排放超标处罚制度的出台，降低污染物排放成为目前电厂追求的另一大目标[11]。从NOx的源头施加控制，降低NOx的生成量可以大大降低脱硝反应器等设备的投入成本。目前，可以通过燃烧设备的改进和优化配风等手段降低NOx的生成量[12-13]。

综上所述，建立的锅炉综合经济指标函数如下：

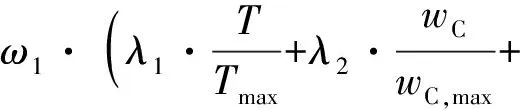
(8)

式中：λ1、λ2和λ3分别为烟温T、飞灰含碳量wC和氧气体积分数φO的权重因子；Tmax为当前一段时间烟温的最高值；wC,max为当前一段时间飞灰含碳量的最高值；φO,max为当前一段时间氧气体积分数的最高值；ω1、ω2为综合经济指标函数中锅炉效率和NOx质量浓度的权重因子；ρmax为当前一段时间内锅炉省煤器后脱硝前NOx质量浓度(ρNOx)的最高值。

2.3 模型的设计

根据优化目标的设计，建立5个鲁棒交叉验证RCV-LSSVM模型，分别对锅炉尾部A、B空气预热器出口烟温、氧气体积分数、飞灰含碳量和脱硝前NOx质量浓度进行预测。建立的锅炉燃烧模型结构如图2所示。将5个参数的预测值代入综合经济指标函数，并结合优化算法可寻得最佳输入参数的组合。

由锅炉燃烧系统输入和输出参数的相关性分析可以得出，空气预热器出口烟温主要受锅炉负荷，总风量，给水量，主、再热汽温以及各给煤机给煤量、各磨煤机一次风量和二次风量等参数的影响；而氧气体积分数、飞灰含碳量和NOx质量浓度主要受改变锅炉燃烧状态的参数的影响，如给煤量，一、二次风量以及各二次风门开度。

图2 锅炉燃烧RCV-LSSVM模型

3 实验结果与分析

3.1 模型预测实验

3.1.1 实验数据

测量空气预热器出口烟温、氧气体积分数和NOx质量浓度的采样周期为1 min，总共取样300组。飞灰含碳量很难实现准确的在线测量，大部分电厂采用化学检验的方法进行离线测量，通常飞灰样品的采样周期是1～2 h，再用经验法对飞灰含碳量进行估计。为了获取建立飞灰含碳量在线软测量的实验数据，将飞灰样品的采样周期缩小到1 min并连续采集300组数据进行化验。同时采集了该时间段内300组锅炉运行参数作为模型的训练和测试数据，包括负荷、总风量、给水量、主汽温、再热汽温和给煤量等40多个输入和输出参数。

3.1.2 结果与分析

取前200组数据作为训练数据，设置鲁棒交叉验证系数S为10，核函数为RBF函数，经过训练，得到A、B空气预热器出口烟温、氧气体积分数、飞灰含碳量和NOx质量浓度5个输出参数的RCV-LSSVM模型；然后再取后面100组数据作为模型的测试数据，用以测试模型对参数的预测效果。图3(a)～图3(d)分别为A空气预热器出口烟温、氧气体积分数、飞灰含碳量和NOx质量浓度的实测数据，RCV-LSSVM模型预测数据以及传统LSSVM模型预测数据的对比效果图。

(a) A空气预热器出口烟温预测效果

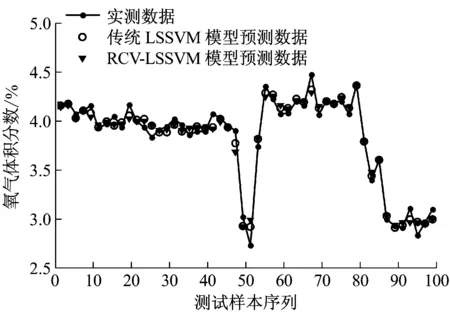
(b) 氧气体积分数预测效果

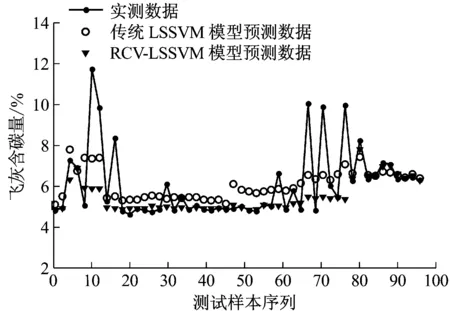
(c) 飞灰含碳量预测效果

(d) NOx质量浓度预测效果

从图3可以看出，RCV-LSSVM模型和传统LSSVM模型对A空气预热器出口烟温、氧气体积分数、飞灰含碳量和NOx质量浓度的预测结果与实测值基本一致，预测效果满足工程应用的要求。对比RCV-LSSVM模型与传统LSSVM模型的预测效果可以发现，RCV-LSSVM模型更适用于测试数据波动大、粗大值较多的情况，说明RCV-LSSVM模型的泛化能力更强，善于处理异常数据，具有鲁棒预测能力。RCV-LSSVM模型是在负荷稳定后建立的稳态模型，当锅炉负荷阶梯式变动后，需要重新建立RCV-LSSVM模型以保证该模型的实时准确性。

表1给出了RCV-LSSVM1模型与传统LSSVM1模型的参数和各自的训练周期。

表1 模型参数和训练周期

从表1可以看出，RCV-LSSVM1模型利用鲁棒交叉验证算法调整正则化参数γ的权重因子，得到n维的正则化参数向量，而传统LSSVM1模型的正则化参数只有一维，通过单一元素验证轮询修改，具有一定的缺陷。

3.2 燃烧优化试验

3.2.1 优化方案

针对350 MW机组当日内负荷变化的特点，制定了如图4所示的优化方案。当负荷平稳时，燃烧优化分3步实施。

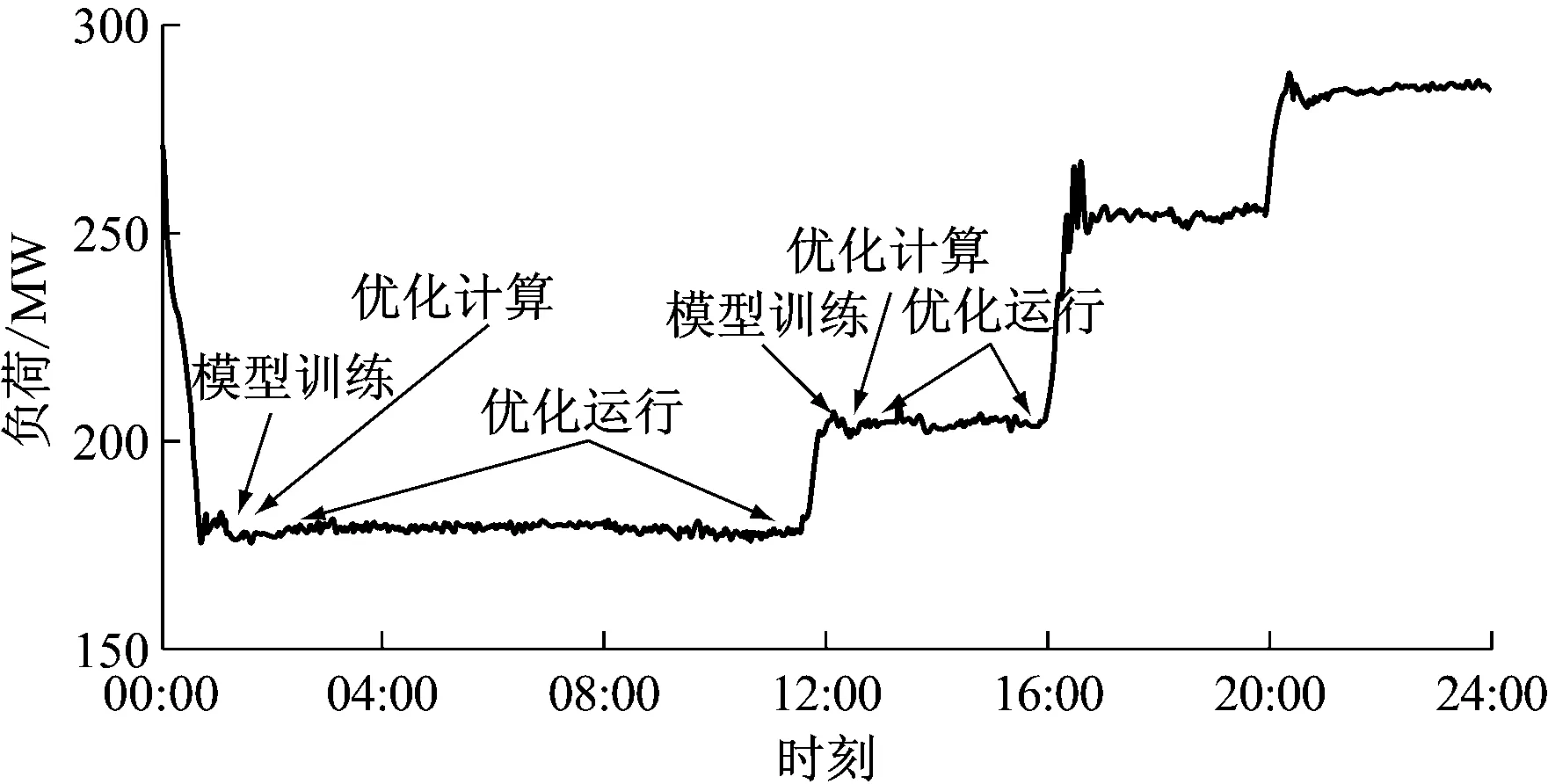
图4 24 h内负荷变化与优化方案

(1) 模型训练阶段。

一般取负荷平稳后30 min内的历史运行数据作为训练样本，保证了模型的实时有效性，为了验证其预测效果，可在模型训练后进行验模。

(2) 优化计算阶段。

采用差分进化(DE)算法进行综合经济指标函数的多参数寻优，DE算法与遗传算法类似，都需要经过变异、交叉和选择3个重要步骤，但DE算法引入了差分矢量对父代参数进行变异操作，利用二项式交叉方法使子代参数值向目标参数值靠拢[14]。相比之下，DE算法寻优效率更高，拥有更好的处理局部极值能力，更适合多目标、多参数的寻优问题。

在DE算法参数寻优过程中，需要根据锅炉燃烧系统风煤总量的变化改变该算法中参数的上下限和约束条件。设置DE算法中的种群数量为200；迭代次数设置为500；寻优参数的维数为22个，包括5个给煤量、5个一次风量和12个二次风门开度。

(3) 优化运行阶段。

当锅炉可调参数优化结果计算得出后，将锅炉给煤参数，一、二次风参数调整为最优参数并运行。直到负荷进入下一个阶段后再重新建模、优化与运行。

3.2.2 结果与分析

表2给出了该机组在某日1:00:00-11:30:00负荷平稳时的燃烧优化试验数据，表中只列出了优化前后部分工况点的参数信息，其中1:30:00-11:30:00为优化运行阶段。

对比机组在优化前后的排烟温度、氧气体积分数、飞灰含碳量及NOx质量浓度的平均值可以发现，优化运行阶段锅炉排烟温度、氧气体积分数、飞灰含碳量及NOx质量浓度分别降低了5%、15%、20%和10%左右。锅炉燃烧系统输入参数的优化方案提高了底层风煤总量，增加了燃尽风量比例，从而改善了在低负荷运行下锅炉内燃料的着火性能和燃尽率。除此之外，优化后炉内整体温度降低，进而降低了NOx的生成量。

4 结 论

(1) 对某350 MW机组锅炉燃烧系统进行机器学习的试验建模，发现鲁棒交叉验证最小二乘支持向量机具有较高的预测精度，改进了传统最小二乘支持向量机模型处理粗大值的能力，提高了模型的泛化能力和鲁棒性。燃烧参数的预测结果显示，RCV-LSSVM模型的预测平均相对误差在5%以下，满足了实际应用的需求。

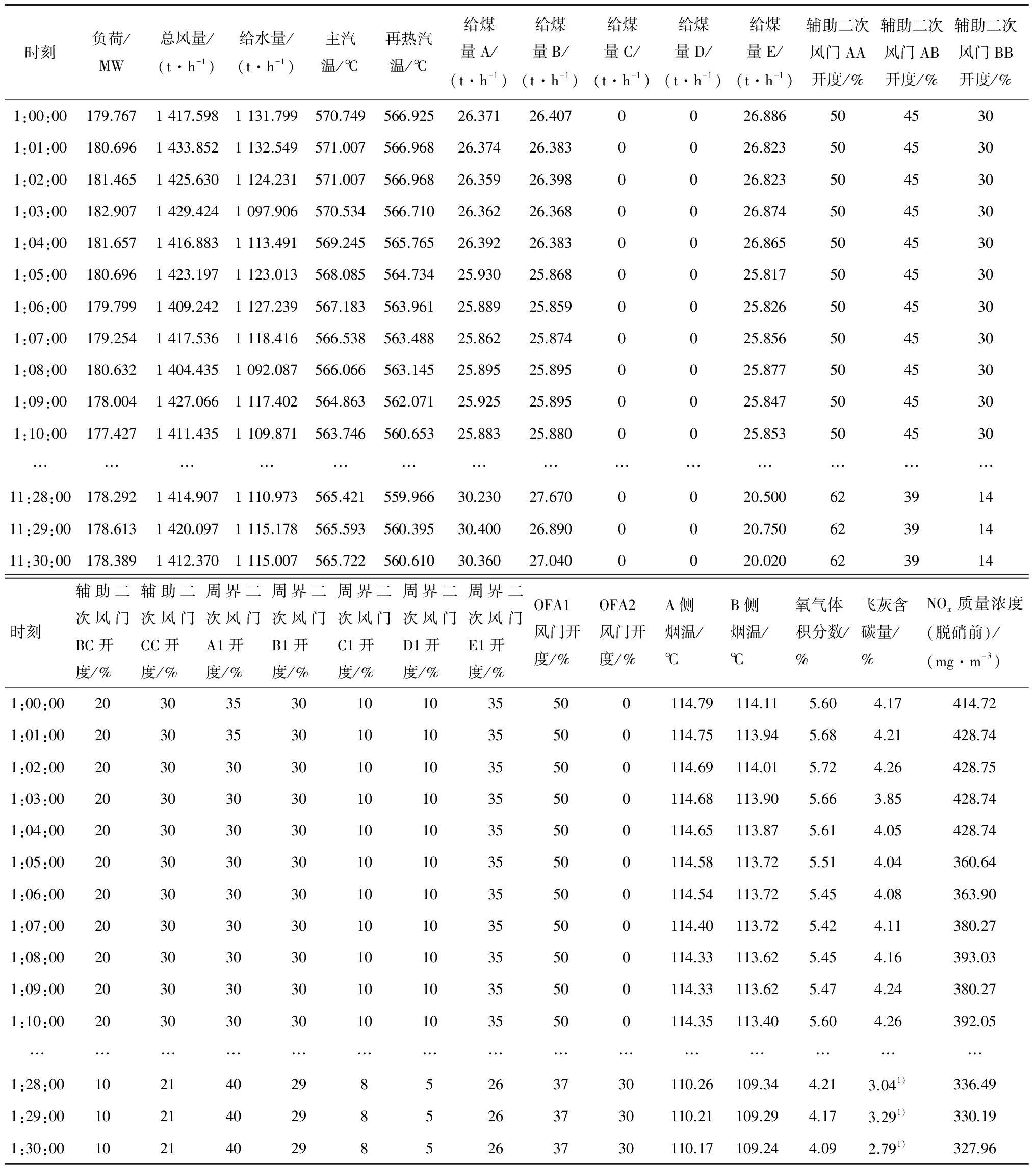
表2 350 MW机组燃烧优化试验数据

注：1) 表示该参数为RCV-LSSVM模型软测量结果

(2) 燃烧优化试验结果表明，通过优化锅炉可调输入参数的组合，锅炉排烟温度、氧气体积分数、飞灰含碳量及NOx质量浓度分别降低了5%、15%、20%和10%左右，提高了锅炉效率并降低了NOx的排放。

致谢：本文的热力实验和实验数据的记录是在陕西华电杨凌热电有限公司工作人员的大力支持下完成，在此向他(她)们表示衷心的感谢。

参考文献：

[1] 刘若晨, 安恩科, 刘泽庆, 等. 全氧煤粉燃烧烟气的辐射特性[J].燃烧科学与技术, 2016, 22(1): 84-90.

LIU Ruochen, AN Enke, LIU Zeqing, et al. Radiation characteristics of oxy-fuel combustion flue gas[J].JournalofCombustionScienceandTechnology, 2016, 22(1): 84-90.

[2] 刘恺. 亚颗粒尺度多相燃烧直接数值模拟[D]. 北京: 清华大学, 2014.

[3] 王禹朋, 阎维平, 祝云飞, 等. 支持向量机理论与遗传算法相结合的300 MW机组锅炉多目标燃烧优化[J].热力发电, 2015, 44(10): 91-96.

WANG Yupeng, YAN Weiping, ZHU Yunfei, et al. Multi-objective combustion optimization for a 300 MW unit using support vector machine theory combining with genetic algorithm[J].ThermalPowerGeneration, 2015, 44(10): 91-96.

[4] 余廷芳, 耿平, 霍二光, 等. 基于智能算法的燃煤电站锅炉燃烧优化[J].动力工程学报, 2016, 36(8): 594-599, 607.

YU Tingfang, GENG Ping, HUO Erguang, et al. Combustion optimization of a coal-fired boiler based on intelligent algorithm[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(8): 594-599, 607.

[5] 高芳, 翟永杰, 卓越, 等. 基于共享最小二乘支持向量机模型的电站锅炉燃烧系统的优化[J].动力工程学报, 2012, 32(12): 928-933, 940.

GAO Fang, ZHAI Yongjie, ZHUO Yue, et al. Combustion optimization for utility boilers based on sharing LSSVM model[J].JournalofChineseSocietyofPowerEngineering, 2012, 32(12): 928-933, 940.

[6] 陈南锟. 基于最小二乘支持向量机的燃煤锅炉燃烧优化研究[D]. 南京: 东南大学, 2016.

[7] BRABANTER K, PELCKMANS K, BRABANTER J, et al. Robustness of kernel based regression: a comparison of iterative weighting schemes[C]//Proceedingsofthe19thInternationalConferenceonArtificialNeuralNetworks:PartI. Limassol, Cyprus: Springer, 2009.

[8] 王金龙, 李恩家. 600 MW燃煤电站锅炉效率和NOx排放浓度多目标优化[J].电站系统工程, 2015, 31(3): 47-48.

WANG Jinlong, LI Enjia. Multi-objective optimization of 600 MW utility boiler efficiency and NOxemission[J].PowerSystemEngineering, 2015, 31(3): 47-48.

[9] 周建新, 方绪文, 孙立永, 等. 基于效益模型的锅炉燃烧综合性能多目标优化[J].动力工程学报, 2015, 35(7): 524-530.

ZHOU Jianxin, FANG Xuwen, SUN Liyong, et al. Multi-objective optimization of comprehensive performance in boiler combustion based on benefit model[J].JournalofChineseSocietyofPowerEngineering, 2015, 35(7): 524-530.

[10] 国家环境保护部. 火电厂大气污染物排放标准: GB 13223—2011[S]. 北京: 中国环境科学出版社, 2012.

[11] 张军, 郑成航, 张涌新, 等. 某1 000 MW燃煤机组超低排放电厂烟气污染物排放测试及其特性分析[J].中国电机工程学报, 2016, 36(5): 1310-1314.

ZHANG Jun, ZHENG Chenghang, ZHANG Yongxin, et al. Experimental investigation of ultra-low pollutants emission characteristics from a 1 000 MW coal-fired power plant[J].ProceedingsoftheCSEE, 2016, 36(5): 1310-1314.

[12] 高鹏, 高明, 张建文, 等. 600 MW机组锅炉低氮燃烧器改造试验研究[J].热力发电, 2013, 42(4): 43-46, 69.

GAO Peng, GAO Ming, ZHANG Jianwen, et al. Experimental study on low NOxcombustion transformation on a 600 MW unit boiler[J].ThermalPowerGeneration, 2013, 42(4): 43-46, 69.

[13] 费俊, 孙锐, 张晓辉, 等. 不同燃烧条件下煤粉锅炉NOx排放特性的试验研究[J].动力工程, 2009, 29(9): 813-817.

FEI Jun, SUN Rui, ZHANG Xiaohui, et al. Characteristics of NOxemission in pulverized coal fired boiler under different combustion conditions[J].JournalofPowerEngineering, 2009, 29(9): 813-817.

[14] 徐斌. 基于差分进化算法的多目标优化方法研究及其应用[D]. 上海: 华东理工大学, 2013.