光脉动法在线测量煤粉粒度分布的实验研究

秦授轩， 蔡小舒

(上海理工大学 能源与动力工程学院，上海 200093)

在电厂运行中煤粉粒度过大或过小都会造成机械不完全燃烧损失增大、锅炉效率下降和磨煤机能耗增加等问题，煤粉浓度不均匀或粒度大小不合适还会导致煤粉管道堵塞，严重时电厂将被迫停机或减负荷以消除堵塞，这给电厂造成重大损失，影响其安全运行。传统的取样离线测量无法实时控制磨煤机及煤粉分离装置的运行。近年来国内外在在线测量煤粉粒度方面进行了不少研究[1-4]，如超声法、zeta电位、图像法和前向散射谱法等。这些方法大多采用在线取样技术，但实际上并不能真实地反映出颗粒在管内流动时的状态。唯一真正的在线方法——超声法又受限于自身机理，测量精度较低。同时这些方法无法直接得到煤粉粒度分布参数，需要通过求得各粒径段累积体积分数之后拟合求得，这从数学上来说必将导致误差变大。因此，寻找一种能够实现真正在线测量煤粉粒度分布参数的技术很有必要。据此，笔者基于光脉动理论和随机理论提出一种算法，可以解决该问题，同时采用小波重构技术解决了原光脉动理论不适用于现场实际测量的问题。

1 基于联合泊松分布的粒度算法

当一束平行光穿过被测颗粒系时，颗粒系造成的消光可由Mie理论描述，在此基础上出现了很多光学测量颗粒的算法和技术。光脉动法是Gregory[5]于1985年提出的一种算法，该算法将测量区内颗粒的统计特性和透射光强的脉动联系起来，从而得到测量区内颗粒的平均粒径和浓度。Gregory认为流过测量区内的单分散颗粒数目概率符合泊松分布，并且泊松分布的参数λ就是测量区内的颗粒数目，即

(1)

式中：Pn为测量区内出现n个颗粒的概率。

对于多分散系来说，不同大小的颗粒流过测量区内的概率依然符合参数为其自身数目的泊松分布，而且每种颗粒是否在测量区内与其他颗粒无关，所以总体上颗粒出现在测量区的概率符合联合泊松分布[6]：P(n)～P(λ1、λ2、…、λn)～P(n1、n2、…、nn)，其中n1,n2,…，nn分别为不同大小的颗粒在测量区内的数目。

对于多分散系，消光和颗粒的大小与浓度存在如下关系[7]：

(2)

式中：I为透射光强；I0为入射光强；ni为不同大小的颗粒在测量区内的数目；ci为对应的颗粒消光截面积；A为测量光束截面积。

对式(2)取方差，联合泊松分布的性质可得到式(3)[8]。

(3)

式(3)中ci可由Mie理论[9]得到：

(4)

式中：D为被测颗粒直径；E为根据Mie理论计算得到的颗粒消光系数；λl为激光波长；m为颗粒折射率。λl和m通常认为是已知的。

假设颗粒粒度分布满足R-R分布[7]，则n可由R-R分布函数给出：

(5)

从式(4)和式(5)可以看出,ni可由D和k表示，而ci可由D表示。这样式(3)中的未知数从ni和ci变为D和k。如果知道了D，那么k就可求解。

在保持被测颗粒总体积不变的情况下，假设多分散系是若干个单分散系之和，且这些单分散颗粒系的体积在多分散系中的比例符合原粒度分布规律。则可以建立式(3)中的2个未知数ni、ci与k的关系：

f(ci，ni)=f(ci,f(k,DV50))=

f(k)=常数

(6)

对于一般电厂煤粉，其粒径上下限基本是已知的，据此可以确定单分散系的上下限。将电厂煤粉简化为5个单分散系，其特征粒径分别为d1=5 μm，d2=25 μm，d3=55 μm，d4=90 μm和d5=120 μm。各单分散系的相对数目为

(7)

根据Gregory理论，测量区内颗粒的浓度和平均粒径DV50可分别由式(8)和式(9)求得：

(8)

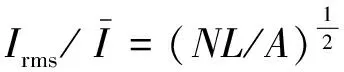
(9)

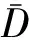
2 实验及结果

为了验证该算法的正确性，笔者进行了模拟验证实验，图1为实验装置照片。

该实验装置包括水-颗粒循环系统、测量段、激光发射和接收部分、数据采集以及计算机信号处理。测量管为12 mm×12 mm的有机玻璃方管，水的体积流量为500～2 500 mL/min。激光发射和信号接收端分置在管道两侧，激光波长为635 nm，标称光斑直径为0.4 mm，接收端使用0.3 mm直径的光纤，后接光电转换装置输出信号，其响应范围为1～5 V。采样系统为12位AD，采样频率为10 kHz。实验颗粒为相对密度0.6，体积中位径20 μm的空心玻璃微珠与混合相对密度为0.9的80 μm乙烯-乙酸乙烯共聚物(EVA)粉末。根据Mie理论，当无因次量α=πd/λ≥100时，颗粒消光系数近似为2，所以在激光波长为635 nm的情况下，这2种颗粒的消光系数都可以认为是2。图2和表1给出了实验颗粒的显微镜照片和图像法测量结果。

图1 实验装置照片

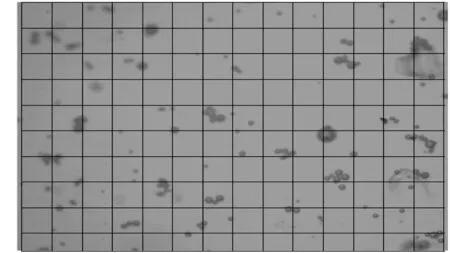
(a) 颗粒图像

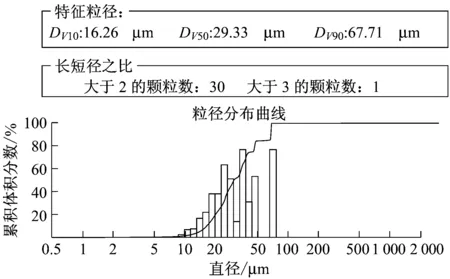
(b) 颗粒粒度累积体积分数

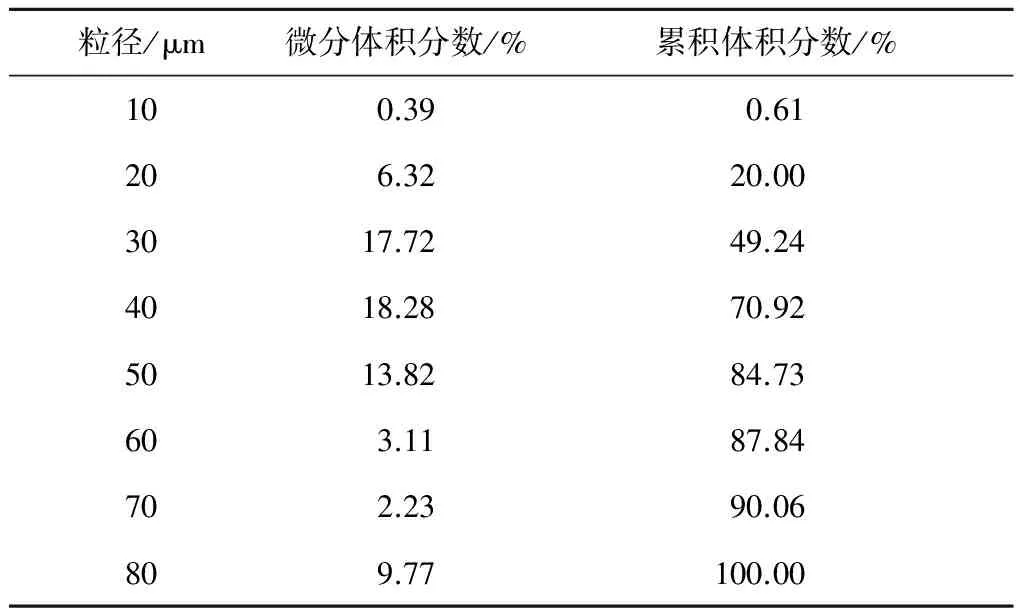
表1 颗粒粒度分布

实验前将0.4 g玻璃珠和1 g EVA粉末放入2 L水中混合均匀。以颗粒平均粒径为25 μm计算，可以得到测量区(为长12 mm，直径0.3 mm的圆柱体)内的颗粒数目约为30。

2.1 实验结果

分别在500 mL/min、1 200 mL/min和2 500 mL/min 3个体积流量工况下进行了实验测量。图3和图4给出了没有颗粒时测得的透射光信号(即原始透射光信号)和有颗粒时测得的透射光信号。

图3 原始透射光信号

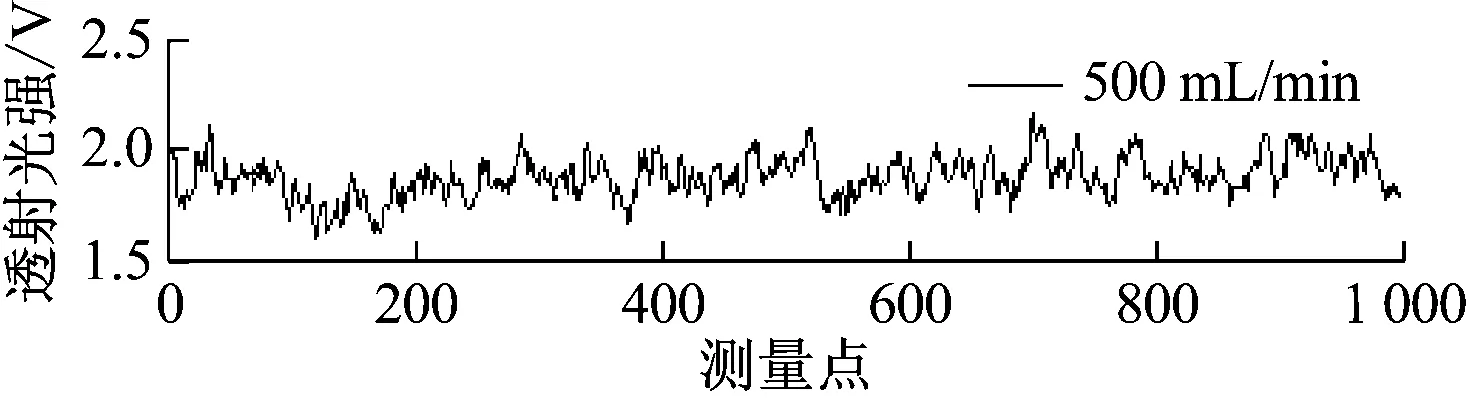
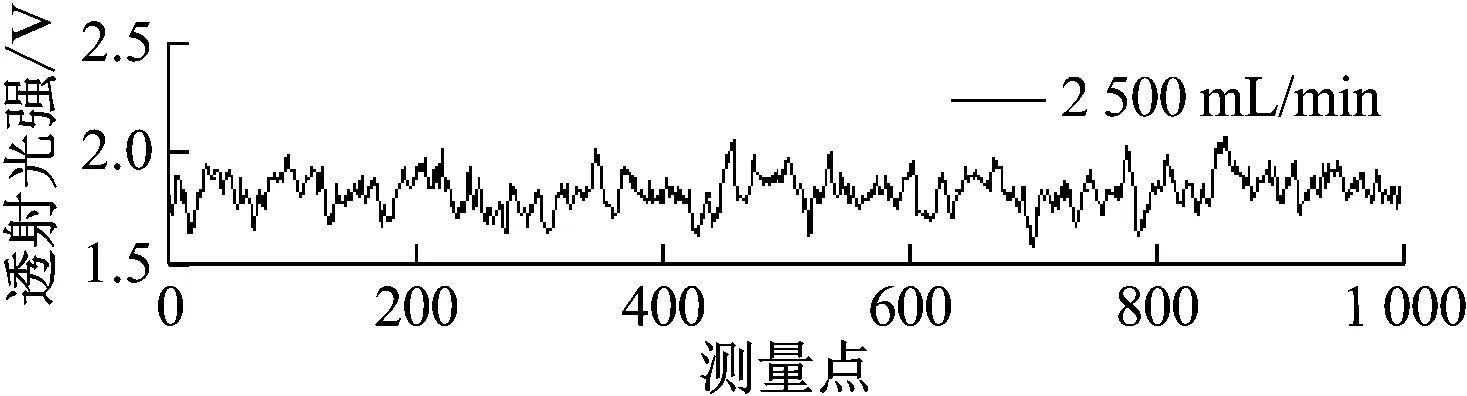
图4 不同工况下透射光信号

从图4可以看出，随着体积流量增大，流速相应变大，信号的脉动程度也加剧，不仅存在小幅度的信号脉动，还存在大幅度的信号脉动，同时随流速增大，透射光强均值也逐渐降低。透射光强均值从1.81降至1.67最后降至1.58。这是因为随着流速增大，湍流程度增加，水带动颗粒流动的能力也增强，颗粒出现在管道中部测量区的概率变大。

2.2 计算结果

表2给出了在3种体积流量下的颗粒粒度计算结果。由表2可知，测量区内平均颗粒数目随体积流量的增大而增加，但DV50和k的值基本一致，没有因为浓度变化而受到较大的影响。测得的DV50平均值为29.30 μm，最大偏差为5.2%，与图像法测量结果偏差仅为0.1%。k的平均值是0.357，最大偏差为3.7%。

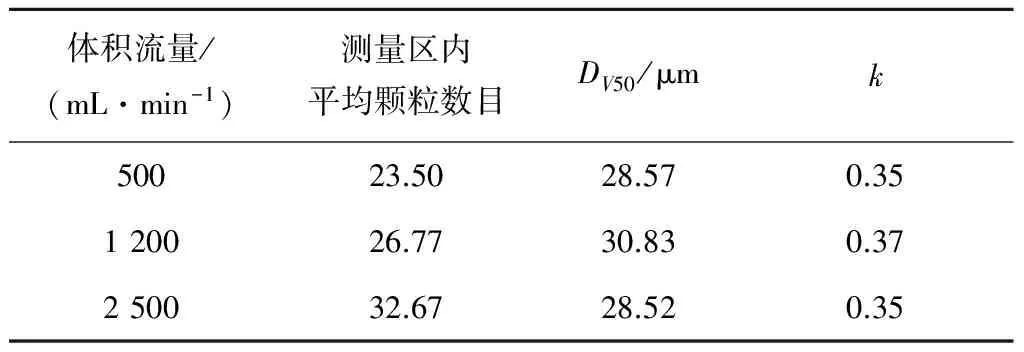
表2 实验颗粒粒度计算结果

2.3 粒度对比及分析

图5给出了计算结果与图像法累积体积分数结果的比较。从图5可以看出，2种测量结果得到的体积中位径及其变化趋势一致。图像法的测量结果是单次测量结果，测量到的颗粒有限，所以其累积体积分数曲线显得不够连续。当采用多次测量的平均结果后累积体积分数曲线会变得平缓，与计算结果更加一致。

图5 计算结果与图像法累积体积分数结果的比较

为验证该方法的可靠性，进行了较长时间的实验，每秒采集一组数据(共1 000组数据)，连续采集40 min，共计获得2 400组数据，然后随机选取100组数据进行处理，结果见图6。

从图6可以看出，即使浓度变化了1倍左右，求得的平均粒度和k基本保持不变，均维持在均值附近，表明该方法基本消除了浓度变化对粒度分布测量结果的影响，可以在浓度大幅度变化的情况下得到被测颗粒的粒度分布。

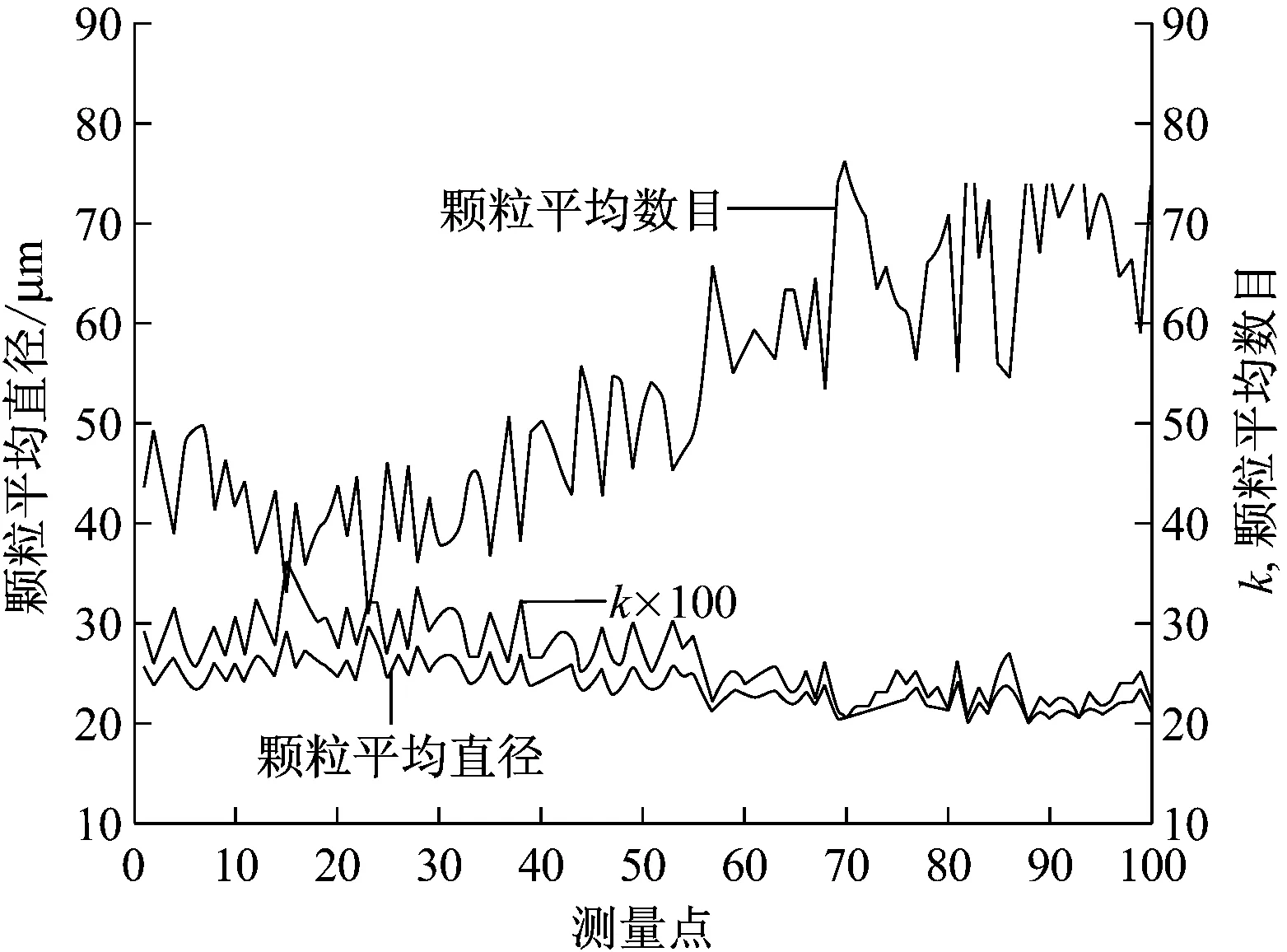
图6 不同浓度时颗粒粒度计算结果

3 电厂煤粉在线测量数据的处理

为了进一步验证该方法，对电厂煤粉在线测量信号进行了处理。图7给出了实测的电厂煤粉透射光信号。从图7可以看出，煤粉的透射光信号变化可以分成2类：一类是变化周期较长，在几个毫秒到几百毫秒之间，但其变化幅度很大；另一类是变化周期很短的高频脉动，其变化幅度不太大。

图7 实测电厂煤粉透射光信号

考虑到在煤粉管中气流速度约为30 m/s，测量光束直径为0.3 mm，按此计算得到的煤粉通过光束的时间约为0.01 ms，远小于长周期大幅度变化信号的时间，因此可以肯定这种长周期大幅度的信号变化是由煤粉浓度变化造成的。

如果将时变的低频浓度信息以及高频的干扰噪音去除，就可以得到有效的煤粉透射光信号。使用最常用的2种滤波方式——带通滤波器和小波重构[10]对信号进行了重构处理，得到的结果见图8。

从图8可以看出，经带通滤波所得信号中的大幅信号占比明显过多，且幅值太大，与实际情况完全不符。如果将其作为实际信号，得到的颗粒平均粒度为120 μm左右，这显然超出了30～50 μm这一煤粉平均粒度的正常范围。而使用小波第五层(d5)重构所得信号的最大幅值与原始透射光强比为0.3左右，而且大小振幅比例符合煤粉粒度变化的规律。

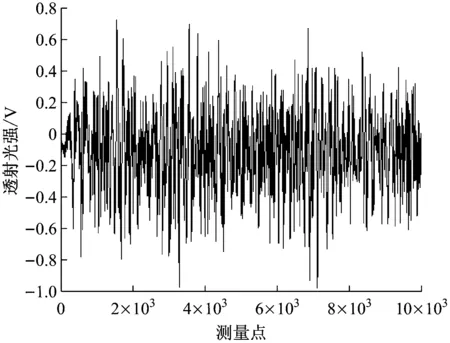
(a)带通信号

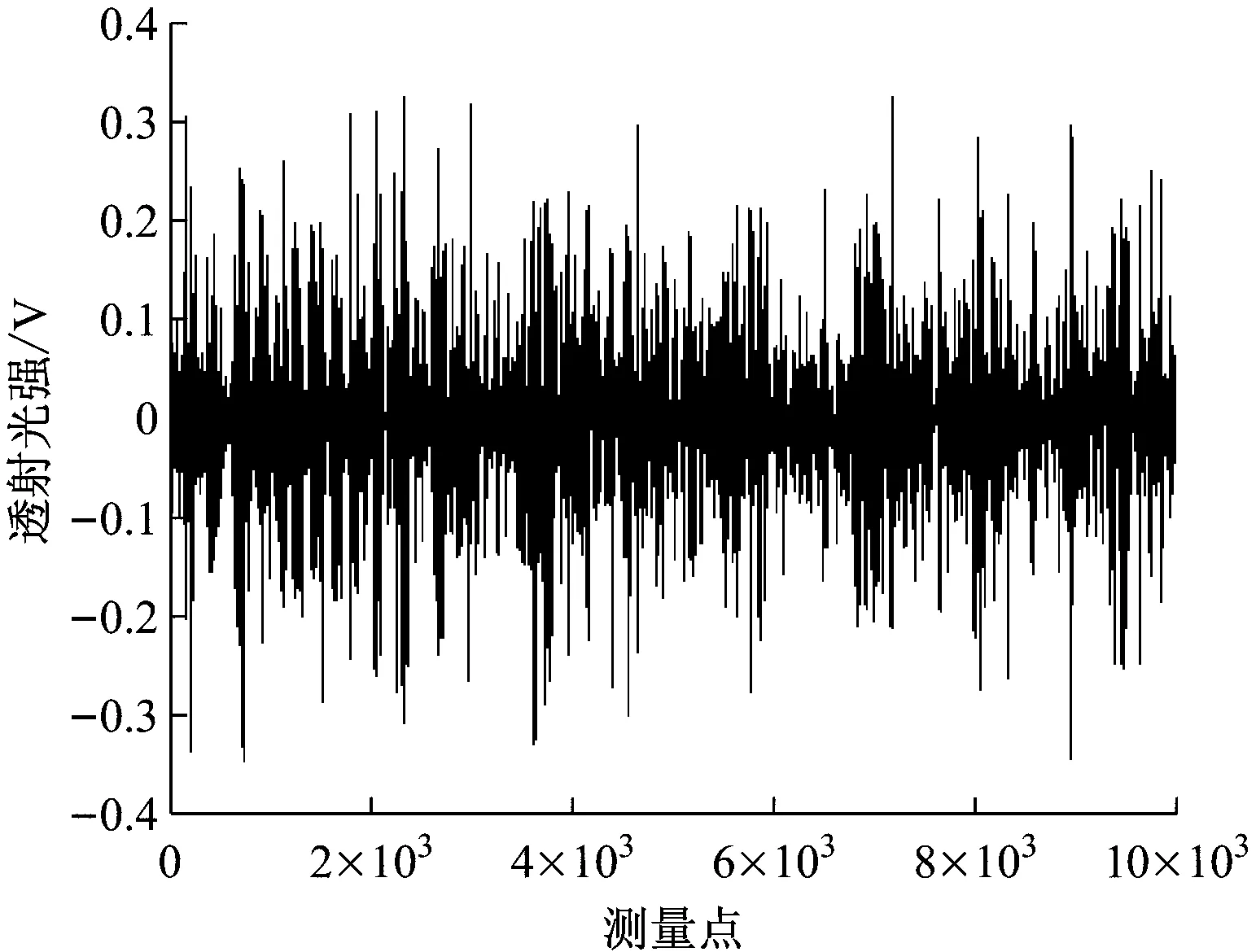
(b)小波分解信号

利用小波重构技术，并结合式(6)的算法对图9数据进行处理。该信号共计51 200个数据，将其按时间均分成5组，得到的结果见表3。

根据表3中的参数，可以得到煤粉频度分布及其累积体积分数。图10给出了该煤粉取样筛分后得到的频度分布及其累积体积分数。从图10可以看出，2种方法的结果吻合很好。

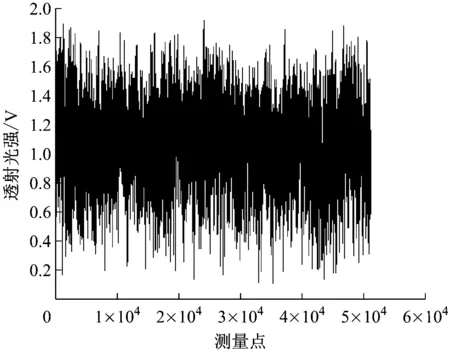
图9 实测电厂信号

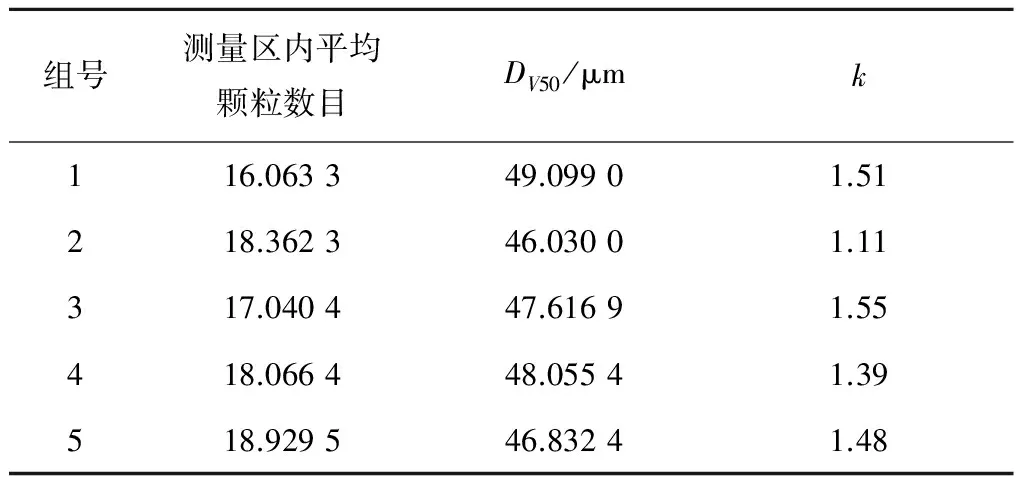
表3 现场煤粉粒度计算结果

4 过采样问题的解决

由于颗粒存在滑移速度，颗粒的速度低于风速，此时如果采用过高的采样频率就会出现过采样的情况。当采样频率过高时，在测量区中的煤粉颗粒还没有全部流出测量区就又被记录了，重复的记录显然会影响信号的均值和方差，从而影响光脉动法的精度。为了得到有效的测量区内颗粒的信息，需要采用小波重构技术来解决过采样的问题。对于图11中的信号，使用和不使用小波重构技术求得的颗粒粒度情况见表4和表5(数据按5 000个为1组进行分组，共分为5组)。

由表4和表5可知，使用小波重构技术后各参数的测量结果变化减小，说明小波重构技术可以去除被测颗粒的浓度变化对测量结果造成的影响，考虑到过采样的后果是多次测量同一颗粒，导致测量结果中颗粒的分布会比较集中。而考察表4和表5可以发现，经小波重构算法后k都变小，颗粒的分布更加分散，说明小波重构技术可以去除过采样带来的影响。

图11 250 kHz采样信号

表4 不使用小波重构技术的处理结果

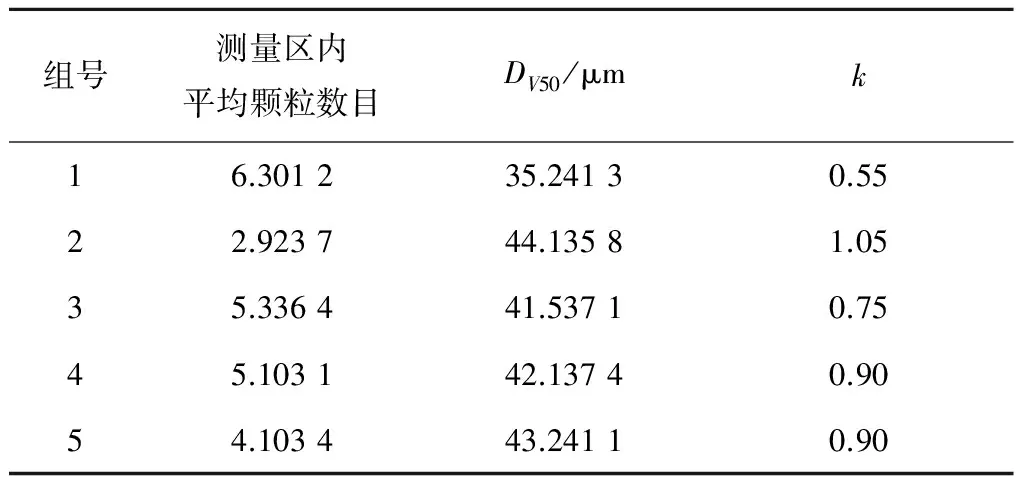
表5 使用小波重构技术的处理结果

5 结 论

(1)根据随机理论和透射光信号的统计特性，求得颗粒粒度分布参数。实验结果表明，这种方法测量结果可信，而且长时间测量时工作稳定，测量结果前后一致，可用于电厂煤粉在线粒度分布和浓度测量。

(2)使用小波重构技术，可以去除颗粒浓度变化对颗粒测量结果造成的影响，还可以去除过采样带来的影响。

参考文献：

[1] YOON J, KIM M, LEE S, et al. Real-time light transmission spectroscopy (RTLTS): a real-time and in situ particle size distribution measurement for fractal-like diesel exhaust particles[J].JournalofAerosolScience, 2015, 90: 124-135.

[2] LIANG Long, WANG Liguang, NGUYEN A V, et al. Heterocoagulation of alumina and quartz studied by zeta potential distribution and particle size distribution measurements[J].PowderTechnology, 2017, 309: 1-12.

[3] SUN Xiaogang, TANG Hong, YUAN Gunbin. Determination of the particle size range in the visible spectrum from spectral extinction measurements[J].MeasurementScienceandTechnology, 2007, 18(11): 3572-3582.

[4] 姜根山, 许伟龙, 安连锁. 声波在电站锅炉含颗粒介质气体中的衰减特性[J].动力工程学报, 2017, 37(2): 126-133.

JIANG Genshan, XU Weilong, AN Liansuo. Attenuation characteristics of acoustic waves in boiler flue gas containing solid particles[J].JournalofChineseSocietyofPowerEngineering, 2017, 37(2): 126-133.

[5] GREGORY J. Turbidity fluctuations in flowing suspensions[J].JournalofColloidandInterfaceScience, 1985, 105(2): 357-371.

[6] ROSS S M. Introduction to probability models[M]. Pittsburgh，USA: Academic Press, 2011.

[7] 王乃宁, 蔡小舒, 郑刚, 等. 颗粒粒径的光学测量技术及应用[M]. 北京: 原子能出版社, 2000.

[8] 祝东进, 郭大伟, 刘晓. 概率论与数理统计[M]. 北京: 国防工业出版社, 2010.

[9] van de HULST H C. Light scattering by small particles[M]. London: Chapman and Hall, 1957.

[10] 高西全, 丁玉美. 数字信号处理[M]. 西安: 西安电子科技大学出版社, 2008.