基于非参数核回归模型的隐含波动率预测
戴秀菊, 舒志彪
(福州大学数学与计算机科学学院, 福建 福州 350116)
0 引言
金融衍生品的隐含波动率能够衡量未来某一段时间内对应的标的资产价格的变动程度, 市场参与者可以据此作出交易决策. 期权隐含波动率是将期权价格代入Black-Scholes期权定价公式[1], 反推得到的标的资产波动率数值. 传统的Black-Scholes公式将隐含波动率σ当做一个恒定常数. 但是, 很多实证分析表明,σ并非一个恒定的常数, 而是与期权的剩余期限和执行价格有着显著相关性的变量[2-3]. 据此, Dumas等[4]构建了隐含波动率参数模型. 该模型假设隐含波动率σ与执行价格K和剩余期限T之间的相关性可以用如下的双二次函数来描述:
lnσ=α0+α1K+α2K2+α3T+α4T2+α5KT+ε
(1)
这种参数模型被广泛研究且扩展[5-7]. 但是参数模型往往需要预先假设波动率与执行价格、 到期日存在某种线性或非线性关系, 这种假设可能会导致较大偏差. 相比之下, 非参数模型显得更加灵活, 它不需要预判因素之间的相关关系, 而只需要做一个最优化拟合. 例如, 毛娟等[8]考虑隐含波动率与剩余期限、 执行价格相关的模型, 采用非参数估计的局部多项式方法来拟合隐含波动率; Borovkova等[9]使用非参数Bourke插值公式构建隐含波动率模型.
基于隐含波动率与期权的剩余期限和执行价格显著相关的假设, 考虑原有的参数模型及Bourke非参数模型的优缺点, 提出两种基于非参数核回归的隐含波动率预测模型: 双窗宽Nadaraya-Watson高斯核回归模型与Parzen-窗均匀核回归模型. 选取AAPL期权数据样本对已有模型与新构建的隐含波动率模型进行实证分析, 并进行预测能力分析. 实验结果表明, 研究提出的基于非参数核回归模型的隐含波动率预测效果更好.
1 非参数核回归模型
所谓回归分析是通过建立回归模型来研究相关变量的关系并作出相应估计和预测的一种统计方法.
定义1(回归模型[10]): 假设有两个随机变量X,Y, 其中X为解释变量,Y为响应变量, 由于变量之间的相关性, 当给定X=x, 响应变量Y不能唯一确定, 仍然为随机变量. 响应变量Y的估计或预测值通常取其条件数学期望E(Y|X=x), 它是解释变量X的函数, 称为回归函数, 记为f(x)=E(Y|X=x), 则回归模型一般形式为:
(2)
其中:f(·)为Y的回归函数;ε为随机误差, 表示除解释变量之外的因素对响应变量的影响.
回归函数f(x)的估计方法一般有参数估计、 非参数估计两种方法. 参数估计预先设置一个模型, 结果的好坏直接取决于模型的预先假设. 而非参数估计不需要进行任何预先设置, 只通过数据决定. 所以相对于参数回归模型, 非参数回归模型的应用范围更广, 性能更稳健.
目前利用非参数估计构建隐含波动率预测模型的方法有很多, 如Borovkova等[9]用非参数插值公式建立隐含波动率模型(简称Bourke模型):
(3)
这个模型基于了一个重要假设: 彼此间距离近的数据点应该有更大的概率成为近邻. 沿用这种思路, 研究将数据之间的相关信息和原有的Nadaraya-Watson核估计与Parzen-窗表示方法相结合, 以此构建两个非参数估计的隐含波动率预测模型. 假设概率大的数据点可以分配到更大的权值, 即对预测样本点的贡献更显著.
2 基于非参数核回归的隐含波动率预测模型
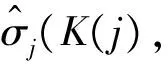
2.1 双窗宽Nadaraya-Watson高斯核回归模型
2.1.1 Nadaraya-Watson核估计[11-16]
定义2假设Xi∈d,i=1, …,N,d为维数,yi∈,i=1, …,N, 存在映射函数f:d→, 使得f(Xi)=yi,i=1, 2, …,N. 又可积函数k(x):→+且k(x)dx=1, 对于任意参数hq>0,q=1, …,d, 有khq(x)=hq-1k(xhq-1), 对h=(h1,h2, …,hd)∈(0, ∞)d, 定义函数kh:d→,kh=kh1⊗kh2⊗…⊗khd, 也就是:
kh(x)≡kh(x1, …,xd)=kh1(x1)…khd(xd)
(4)

(5)
Nadaraya-Watson估计可以看作是一种简单的加权平均, 即:
(6)
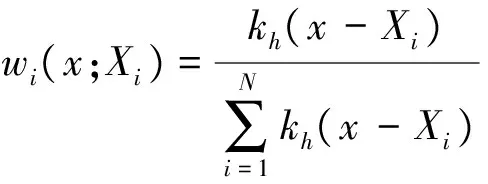
(7)
上述光滑参数hq是一个与N有关的正常数, 满足N趋于无穷时,hq趋于0,k(·)为已知核函数. 光滑参数hq的选取会直接影响到模型的估计精度. 光滑参数hq太小, 则有用信息和干扰信息无法分离, 拟合方差较大, 容易导致除样本点外, 其它点处均为零. 反之, 光滑参数hq太大, 则会导致估计过度平均化, 偏差和残差较大. 估计隐含波动率时, 一般希望有较高精度和较小的偏差, 因此光滑参数hq的选取尤为重要. 光滑参数的处理见节3.2.
2.1.2 双窗宽Nadaraya-Watson高斯核回归隐含波动率预测模型
Bourke模型的权重使用的是距离的倒数, 距离越近权重越大. 但是, 当待测点的剩余期限和执行价格与某一已知样本点的剩余期限和执行价格相等时, 该点的权重为无穷. 为了避免这个问题, 研究使用非参数双窗宽Nadaraya-Watson高斯核回归模型. 即核函数k(·)取用高斯核函数:
(8)
在隐含波动率预测模型中, (8)式中x={K,T}. 根据定义及式(4)、 (5)和(8), 隐含波动率估计公式为:
(9)
2.2 Parzen-窗均匀核回归模型
2.2.1 Parzen-窗估计[17-18]
(10)
其中:N为样本个数;m为落入小舱中的样本个数;V为舱体积.
假设x是d维空间中任意一点, 每个小舱是一个超立方体, 它在每一维的棱长表示为hq,q=1, 2, …,d, 则小舱的体积是V=h1,h2, …,hd. 要计算落入以x为中心的小舱内的样本数目, 可以定义如下的d维核函数:
(11)
因此,X落入以x为中心的超立方体内的样本数:
(12)
2.2.2 Parzen-窗均匀核回归隐含波动率预测模型
双窗宽Nadaraya-Watson高斯核回归模型使用所有的样本点, 而样本点对应的隐含波动率差异较大, 导致某些点虽然权重很小, 但是对结果贡献仍然很大. Bourke模型也存在同样问题.
针对以上问题, 研究进一步提出使用Parzen-窗均匀核密度估计法, 公式如下:
(13)
同理, 在隐含波动率预测模型中, (13)式中x={K,T}, 所以得到隐含波动率估计:
(14)
也就是说, 单个待测点不是和全部样本点都有关系, 而是只跟待测点附近的少量样本点有关, 而且它们的权重是相等的.
2.3 基于非参数核回归的隐含波动率预测模型分析
实际生活中的数据彼此之间往往存在着或多或少的相关性. 在研究某事物时, 为了能够更全面、 准确地表述它, 应考虑更多与该事物相关的变量. 期权数据也不例外, 经过大量实证分析, 期权隐含波动率与执行价格、 剩余期限有着较强的相关性. 根据不同执行价格和剩余期限两个变量彼此间各自的距离远近来表示隐含波动率之间的相关性强弱, 用非参数核回归的方法反映隐含波动率之间的相关性. 在Bourke模型(3)与本研究提出的双窗宽Nadaraya-Watson高斯核回归隐含波动率预测模型(9)、 Parzen-窗均匀核回归隐含波动率预测模型(14)等3个模型中, 根据K、T的距离远近, 给定不同的核密度估计表示它们的相关性, 如图1所示. 为了更直观明了, 这里只给出K方向的剖面, 同理,T方向样本点隐含波动率的相关性也可由相同的剖面表示.
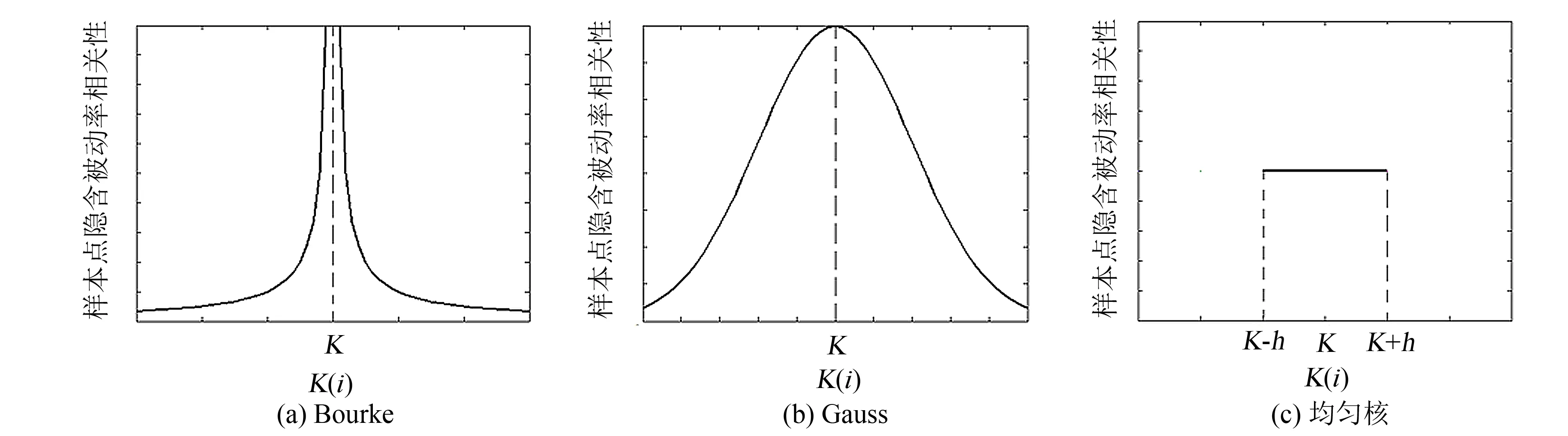
图1 3种模型的样本相关性示意图Fig.1 Sample correlation diagram of the three models
从图1可以直观地看出Borovkova等的Bourke模型和双窗宽Nadaraya-Watson高斯核模型都考虑了全部的样本点, 导致某些样本点虽然相关性很小, 但是由于自身取值较大, 所以对预测结果的贡献仍然很大. 而且Bourke模型会出现奇异点, 导致结果会出现奇异, 不如高斯核模型. 与这两种模型相比, Parzen-窗均匀核模型只考虑局部样本点, 数据相关性表示更合理, 预测更准确, 具体可由以下实验得证.
3 实验与分析
将双窗宽Nadaraya-Watson高斯核回归模型(9)和Parzen-窗均匀核回归模型(14)与已有的参数模型(1)、 Bourke模型(3)进行对比实验. 从预测精确度的角度进行分析, 分别给出4种模型的预测误差.
3.1 数据集
实验使用从雅虎网站(http://finance.yahoo.com/q/op?s=AAPL+Options)下载的AAPL期权数据. 实验分为大样本测试和小样本测试. 小样本点集来自2015年11月25日至2015年12月09日两周的数据, 测试数据来自2015年12月14日当天的数据. 大样本点集来自2015年12月26日至2016年2月29日3个月全部的数据, 测试数据来自2016年3月1日和2016年3月2日两天的数据. 小样本点集有3 018个数据, 大样本集有2万个左右数据. 这里只给出预测集2016年3月1日当天的部分数据. 数据集整理如表1所示.
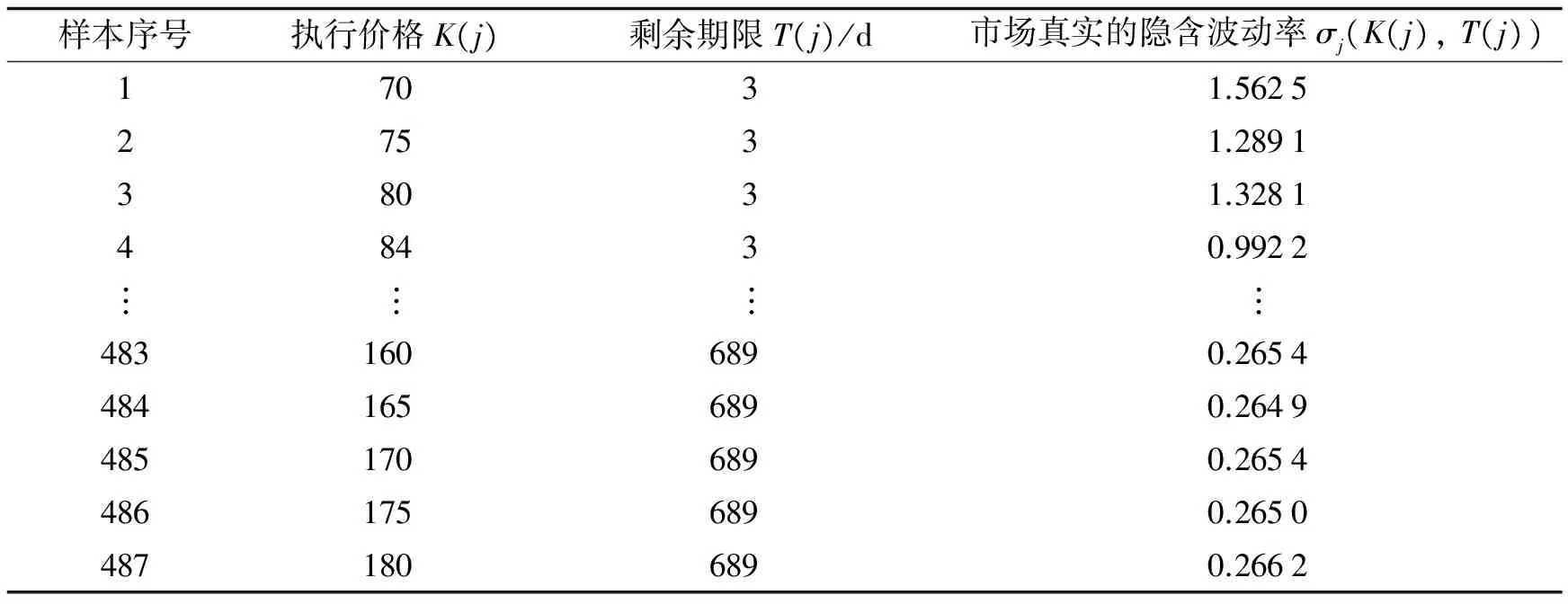
表1 2016年3月1日AAPL期权待测样本数据集
3.2 窗宽选择
窗宽hd与样本容量大小有关, 窗宽的选取直接影响到估计精度. 在实践中, 采用Silverman[19]的经验法则计算最优窗宽, 计算公式为:
(15)
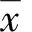
3.3 实验结果与分析
预测实验误差的计算公式为:
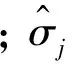
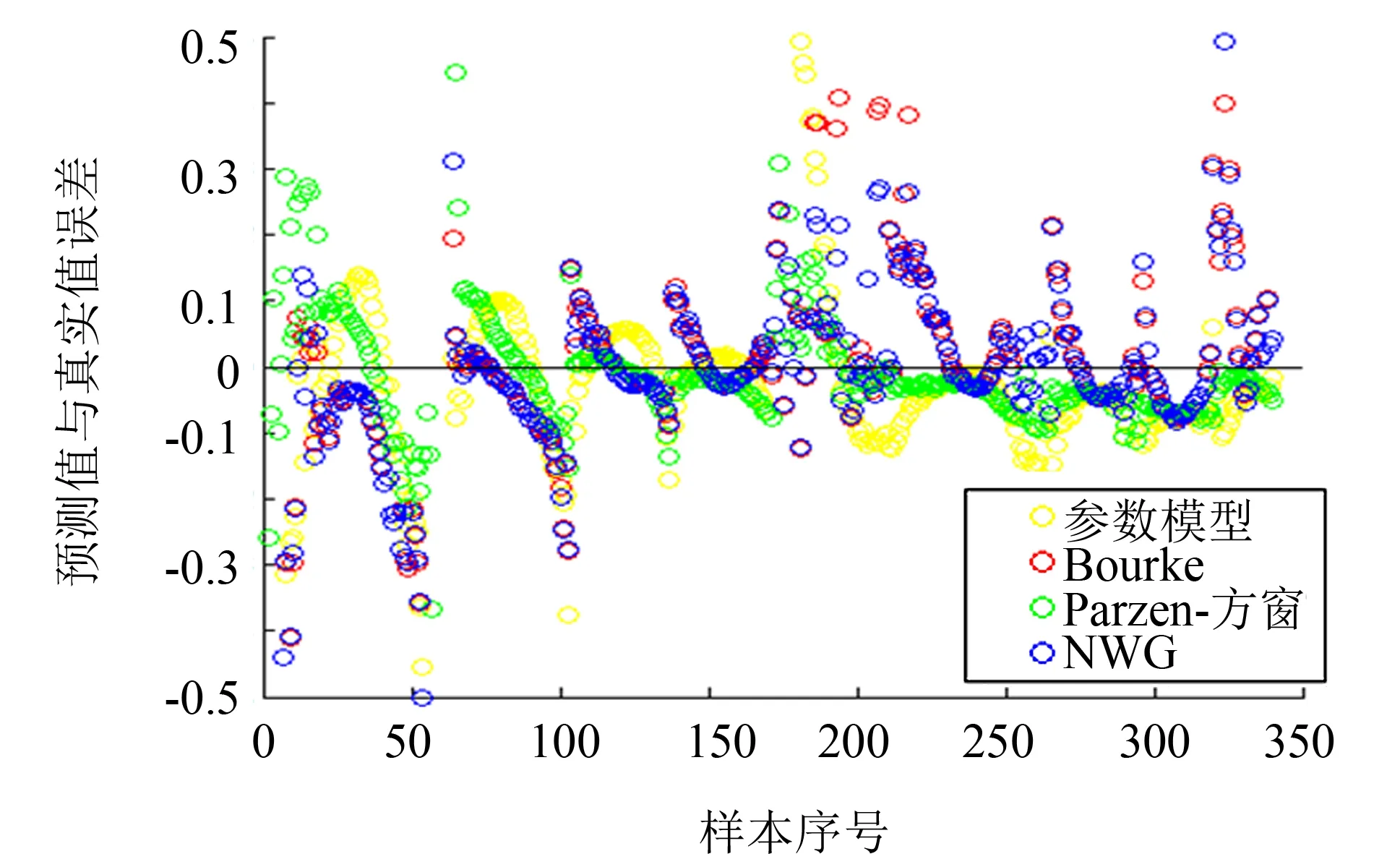
图2 AAPL期权隐含波动率预测误差分布图(2015—12—14)Fig.2 Implied volatility prediction error distribution of AAPL options on December 14, 2015
表2的实验数据样本点来自2015年11月26日—2015年12月9日剩余期限小于100 d的3 018个数据, 测试数据来自2015年12月14日剩余期限小于100的340个数据. 图2为2015年12月14日4种模型的隐含波动率预测误差分布图.
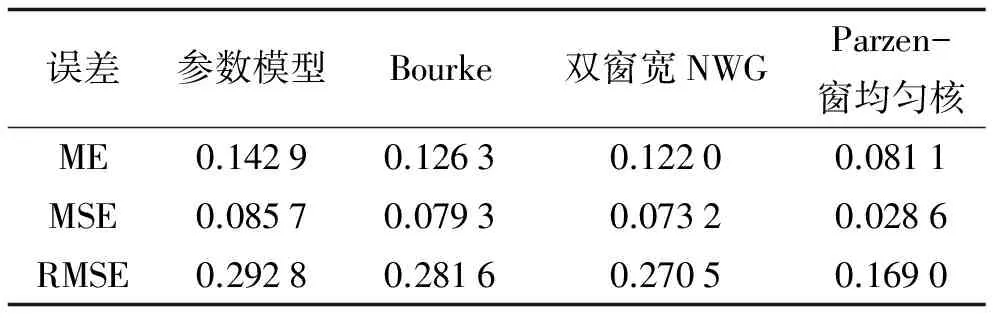
表2 4种模型预测误差对比(2015—12—14)
表3、 4的实验数据样本点来自2015年12月26日—2016年2月29日3个月全部的数据, 测试数据分别来自2016年3月1日和2016年3月2日当天的数据. 图3、 4分别为2016年3月1日与2016年3月2日的真实隐含波动率与模型隐含波动率的误差分布图.
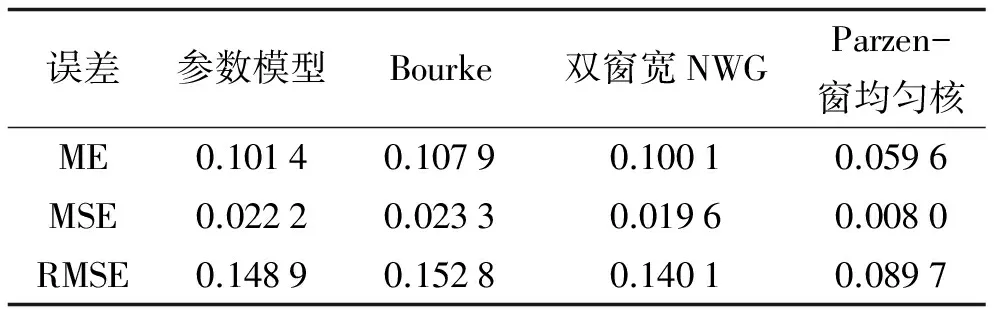
表3 4种模型预测误差对比(2016—03—01)

表4 4种模型预测误差对比(2016—03—02)
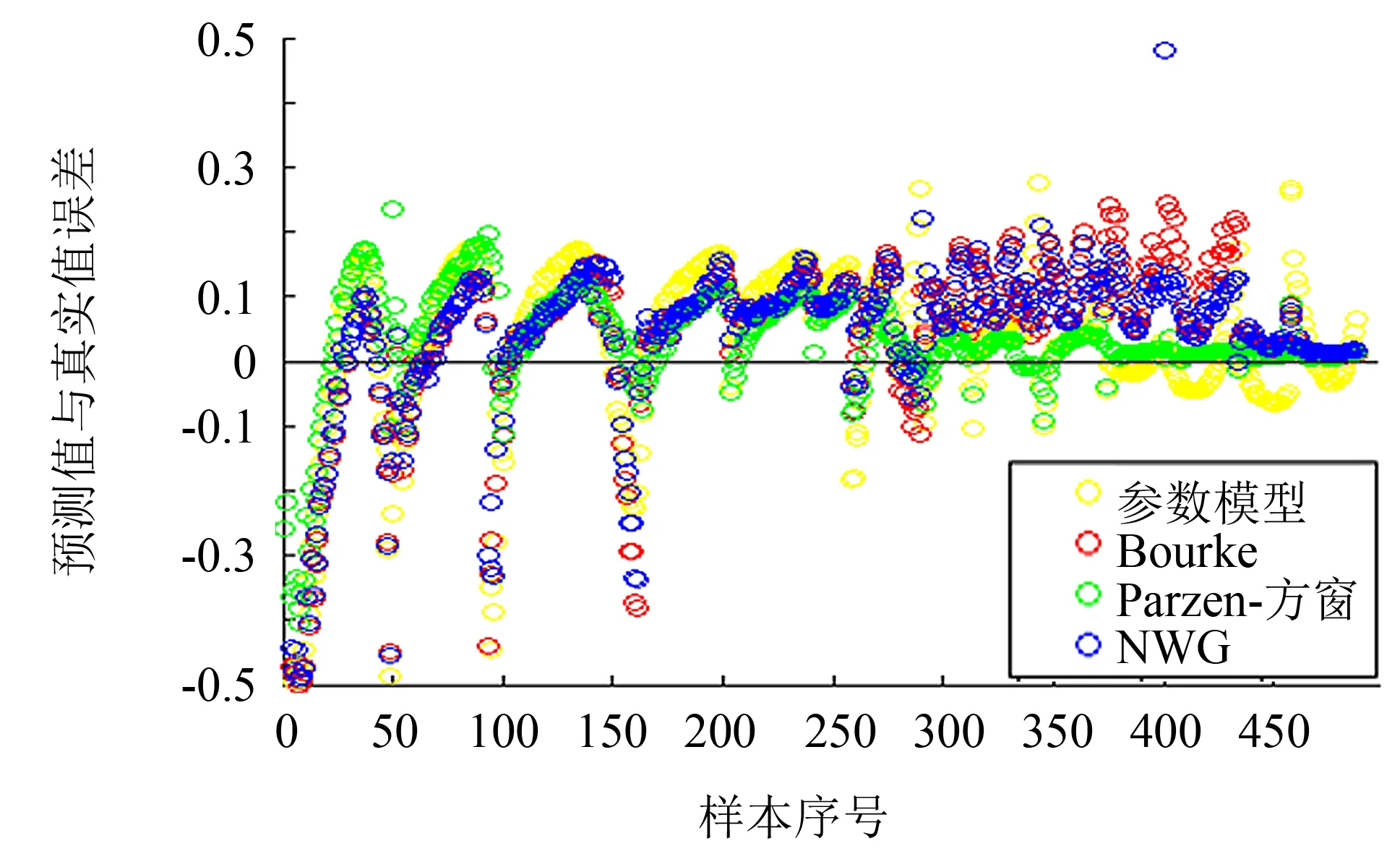
图3 AAPL期权隐含波动率预测误差分布图(2016—03—01)Fig.3 Implied volatility prediction error distribution of AAPL options on March 01, 2016

图4 AAPL期权隐含波动率预测误差分布图(2016—03—02)Fig.4 Implied volatility prediction error distribution of AAPL options on March 02, 2016
实例研究表明, 与参数模型相比, 非参数模型不需要预先假定回归函数形式, 对数据的分布一般不做任何要求, 所以模型精度较高, 且在大样本的情况下效果更好. 与Dumas的参数模型、 Bourke模型、 双窗宽Nadaraya-Watson高斯核回归模型相比, Parzen-窗均匀核隐含波动率模型能够较好地筛选掉与待测点无关的样本点, 在不同的样本容量下预测误差较小, 整体预测效果更好.
4 结语
Parzen-窗均匀核模型与双窗宽Nadaraya-Watson高斯核回归模型是非参数核回归模型. 这两个模型采用了Bourke模型权重的思想, 克服了参数模型预先假设变量间关系导致较大偏差的缺点, 此外, 还克服了Bourke模型的某些点的权重为无穷的缺点. 双窗宽Nadaraya-Watson高斯核回归模型认为对于单个待测点的预测与全部的样本点都有关系. 而Parzen-窗均匀核回归模型待测点只与附近的样本点有关, 这种局部思想更符合实际且实验效果更好. 不过, 本研究的模型仅考虑了隐含波动率与期权的剩余期限和执行价格的关系, 今后的研究将进一步考虑期权的交易频率、 数量及标的资产价格服从跳跃过程等因素对隐含波动率的影响.
参考文献:
[1] BLACK F, SCHOLES M. The pricing of options and corporate liabilities[J]. Journal of Political Economy, 1973, 81(3): 637-654.
[2] NCUBE M. Modelling implied volatility with OLS and panel data models[J]. Journal of Banking & Finance, 1996, 20(1): 71-84.
[3] FENGLER M R. Option data and modeling BSM implied volatility[M]. Berlin: Springer, 2012.
[4] DUMAS B, FLEMING J, WHALEY R E. Implied volatility functions: empirical tests[J]. Journal of Finance, 1998, 53(6): 2 059-2 106.
[5] 莫旭华. 基于香港股票期权的隐含波动率建模[D]. 广州: 华南理工大学, 2012.
[6] ZHAO B, HODGES S D. Parametric modeling of implied smile functions: a generalized SVI model[J]. Review of Derivatives Research, 2013, 16(1): 53-77.
[7] GATHERAL J, JACQUIER A. Arbitrage-free SVI volatility surfaces[J]. Quantitative Finance, 2013, 14(1): 59-71.
[8] 毛娟, 王建华. 隐含波动率曲面的非参数拟合[J]. 武汉理工大学学报(信息与管理工程版), 2009, 31(2): 197-199.
[9] BOROVKOVA S, PERMANA F J. Implied volatility in oil markets[J]. Computational Statistics & Data Analysis, 2009, 53(6): 2 022-2 039.
[10] JOHNSON R A, WICHERN D W. 实用多元统计分析[M]. 6版. 陈旋, 等译. 北京: 清华大学出版社, 2008.
[11] NADARAYA E A. On estimating regression[J]. Theory of Probability & Its Applications, 1964, 9(1): 141-142.
[12] WATSON G S. Smooth regression analysis[J]. Sankhyā: The Indian Journal of Statistics, Series A, 1964, 26(4): 359-372.
[13] KENMOE R N, SANFELICI S. An application of nonparametric volatility estimators to option pricing[J]. Decisions in Economics and Finance, 2014, 37(2): 393-412.
[14] TSYBAKOV A B. Introduction to nonparametric estimation[M]. New York: Springer-Verlag, 2009.
[15] HOLCAPEK M, TICHY T. An application of ann-dimensional fuzzy smoothing filter in financial modeling[C]//Business Engineering and Industrial Applications Colloquium. Kuala Lumpur: IEEE, 2012: 226-231.
[16] KUNG J J. A nonparametric kernel regression approach for pricing options on stock market index[J]. Applied Economics, 2016, 48(10): 902-913.
[17] 张学工. 模式识别[M]. 3版. 北京: 清华大学出版社, 2010.
[18] MUSSA H Y, MITCHELL J B O, AFZAL A M. The Parzen window method: in terms of two vectors and one matrix[J]. Pattern Recognition Letters, 2015, 63: 30-35.
[19] SILVERMAN B W. Density estimation for statistics and data analysis[M]. London: CRC press, 1986.

