角速度信号在功能性电刺激系统步态分段算法中的应用

陈建国， 杨 徐， 李玉榕

(福州大学电气工程与自动化学院， 福建省医疗器械和医药技术重点实验室， 福建 福州 350116)

0 引言

近年来， 脑卒中(脑中风)或外伤引起的足下垂患者数量逐年增多. 足下垂(foot drop)是指患者踝关节无法产生背屈， 走路时无法使脚背弯起的症状. 足下垂患者在行走时脚趾拖地， 与正常人的下肢差异很大， 不仅行走不便， 而且容易摔倒. 如果在康复训练时摔倒更易导致二次中风， 后果将更加严重. 因此, 如何利用新技术、 采用新方法使足下垂康复治疗仪体积更小、 功能更健全、 使用更方便， 帮助患者恢复正常的行走能力， 减少其对家人和医护人员的依赖， 对于足下垂患者本人和家庭而言具有重要的意义， 同时能产生良好的社会效益. 功能性电刺激是目前应用最为广泛的足下垂康复治疗方法之一， 通过在患者行走的摆动阶段以低频脉冲电流刺激胫骨前肌， 促进胫骨前肌主动收缩， 使足部产生背屈运动， 从而治疗足下垂[1]. 相比其他康复治疗方法， 功能性电刺激可以使患者行走时更加自信、 步态更稳健且不易疲劳. 步态即为人体走路时的姿态， 包含了许多运动信息， 步态信息的分段在功能性电刺激中起着非常重要的作用. 目前， 步态分段方法存在识别率低、 实时性差、 过于复杂等缺点. 如何利用采集到的步态数据进行步态分段， 实时识别出步态的摆动相和站立相， 是应用功能性电刺激治疗足下垂的关键因素.

荷兰生物医学技术研究所的Monaghan C C等[2]采用阈值分类法， 将采集到的角速度进行积分得到角度， 通过设定阈值来进行步态分段. 该方法的积分计算会带来累积误差， 容易导致误判. 为解决积分带来的误差问题， 英国牛津大学的Morri[3]采用一个步态周期的起始和结束时刻的角度相等且此时脚的速度为零的方法来进行步态分段， 但其有效性和实时性需进一步验证. 台湾大学的SHIHY Y等[4]利用神经网络算法将传感器测得的角度进行训练， 识别出步态周期的各个阶段， 并采用PID控制功能性电刺激的输出. 此方法虽然能够进行实时步态分段， 但每个患者使用前都必须先用传感器采集步态信息进行训练， 所以使用起来比较复杂. 马来西亚莫纳什大学的Gouwand[5]利用角速度信号对步态周期各阶段进行识别， 大连理工大学的韩宁[6]将传感器采集到的角速度用基于知识的步态分段算法进行步态分段. 虽然两者能够比较准确地识别出步态各个阶段， 误差小， 但是此算法中判断前一个步态阶段需要依赖于后一个步态阶段的数据， 实时性差. 大连理工大学的Wang和Qiu等[7]将加速度和角速度信号采用滑动方差法， 即分别对加速度和角速度求方差作为阈值， 对一个周期内的步态各阶段进行识别， 分别是脚跟离地、 摆动相、 脚跟着地以及完全站立. 该算法需要采集所有数据后才能求方差， 不能实现一边采集数据一边进行步态识别， 因此不能应用到实时功能性电刺激治疗中. 丹麦奥尔堡卫生科技部的Jan Rueterbories和Erika G Spaich[8]采用步态相位检测方法， 虽然步态分段时有较好的实时性， 但是系统容易受到患者跛行步态影响， 导致较高的错误率.

本研究提出的基于角速度信号的步态分段算法不需要积分运算， 避免了累积误差， 算法简单且准确性较高， 最重要的是该算法实时性好， 能够为研究穿戴式功能性电刺激系统提供基础与保证.

1 系统总体设计方案

本研究为基于阈值步态分段算法的功能性电刺激系统， 系统总体方案如图1所示. 将穿戴下肢的MPU6050传感器采集到的数据通过I2C传输到CC2541单片机中， 然后采用步态分段算法进行处理， 并控制功能性电刺激的输出. 当检测到脚跟离地时， 控制功能性电刺激模块对足下垂患者的胫前肌施加电刺激信号， 促进踝关节产生背屈； 当检测到脚跟着地时， 停止电刺激输出信号， 使患者能够正常行走， 从而治疗足下垂患者.

图1 系统总体方案图Fig.1 Overall scheme of the system

2 基于阈值的角速度步态分段算法

2.1 步态周期分析

图2 正常人步态周期的时间分解Fig.2 Time breakdown of normal gait cycle

人的步行过程是一个有规律的模式， 对于规律的运动而言可以研究其周期性. 一个步态周期是指在行走过程中， 从一只脚完全站立在地面上到这只脚再次完全站立在地面上所经历的时间. 一个完整的步态周期可以分为三个阶段： 站立阶段、 推动阶段、 摆动阶段[9]， 如图2所示. 文[10]研究表明， 正常人的步态周期约1.3 s， 其中站立阶段的时间约620 ms， 从脚跟离地到脚尖离地有一个力推动过程， 约200 ms， 摆动阶段的时间约470 ms.

脚跟离地(heel off， HO)是推动阶段的起点， 也是站立阶段的终点. 脚尖离地(toe off， TO)是摆动阶段的起点， 也是推动阶段的终点. 脚跟着地(heel strike， HS)是站立阶段的起始， 也即摆动阶段终点的标志. 功能性电刺激通过在行走步态的摆动阶段刺激胫骨前肌从而治疗足下垂， 也就是需要在HO时刻开启电刺激， 在HS时刻停止电刺激. 因此， 为了正确控制功能性电刺激输出， 需要研究步态分段算法， 实时确定HO时刻和HS时刻.

在功能性电刺激时， 刺激的开启时刻尤为重要， 因为如果足下垂患者脚尖已经离地， 而此时如果胫骨前肌仍旧无力的话， 会导致患者重心不稳而跌倒. 相关实验研究表明[11-12]， 肌肉在外部电刺激作用下从零肌肉力输出到最大肌肉力输出需要一定时间， 包括电信号在肌肉的传输延迟和肌肉本身的反应时间， 大约50～150 ms， 个体有差异， 如图2中阴影部分所示. 因此， 实际应用中， 应当选择脚尖离地TO时刻的前50～150 ms的时刻作为电刺激的起点. 考虑到寻找该特征点时， 算法本身会存在时延， 因此， 在选择功能性电刺激起点时， 必须再加上算法的延时. 可以选择推动阶段的起点， 即脚跟离地HO时刻作为电刺激起点. 而功能性电刺激的结束时刻的准确性相比较而言可以放松些， 因为即使脚跟着地后， 电刺激仍然存在， 患者只是感觉上有一点不舒服， 不至于发生危险.

2.2 步态数据分析

从文[13]可以得出， 平地自由行走模式下将传感器穿戴于小腿和踝关节， 其矢状面(通过人体沿垂轴和纵轴的平面及与其平行的所有平面都称为矢状面)角速度幅值大、 变化比较均匀、 规律性明显、 易于寻找特征点. 而且穿戴于小腿的不同位置， 角速度数据规律性一致， 故小腿以及踝关节可以认为是传感器的理想穿戴位置， 而且小腿穿戴位置的变化不至于影响结果， 这样便于患者使用时可选择在小腿上某个舒适的位置穿戴.

在本次步态数据采集实验的过程中， 选择8名志愿者参与实验， 其中男女各四名. 为验证所设计的系统可以利用步态分段算法的识别结果实现功能性电刺激的正确输出， 选择了健康的志愿者， 后续阶段的研究将针对不同类别的足下垂患者进行实验. 实验过程中志愿者们均穿着跑步鞋， 并在指定位置穿戴好步态测量的传感器， 以在直线自由行走大约10 m和在跑步机上以不同速度行走两种情况来进行步态数据采集. 由于此系统主要用于足下垂患者康复训练， 所以要求志愿者们在实验中步行速度尽量放慢.

采集数据时， 为研究传感器不同穿戴位置对步态分段结果的影响， 需将采集数据的传感器穿戴在下肢的各个部位. 因此， 研究前期将系统穿戴在人体下肢， 一边采集数据一边将其储存在单片机中. 步态实验结束后再将数据通过串口调试助手传输到计算机， 用Matlab软件进行处理， 寻找最优传感器穿戴位置及进行算法研究. 最终再将算法在单片机系统中实现， 以实现实时控制.

通过分析人体的行走特点可以发现， 人行走时的角速度信号规律比加速度信号规律更明显， 利用角速度划分三个阶段的步态周期更简便[14]. 而且实验所利用的陀螺仪， 又称之为角速度传感器， 基本能够消除重力对运动的影响， 并且噪声很小[15]. 因此， 采用角速度信号作为步态分析的特征数据.

2.3 步态分段算法的实现

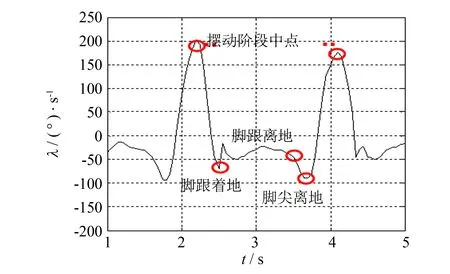
图3 一个步态周期矢状面角速度变化曲线 Fig.3 Angular velocity of sagittal plane in one gait cycle

从图2可以发现， 一个完整的步态周期可以分为三个阶段： 站立阶段、 推动阶段和摆动阶段. 推动阶段前的时刻为脚跟离地HO时刻， 站立阶段前的时刻为脚跟着地HS时刻， 通过本章2.1小节的分析， 可以将脚跟离地HO和脚跟着地HS时刻分别作为功能性电刺激开启和关断的时刻. 因此， 需要找到合适的算法确定出两个关键的时刻： 脚跟离地HO和脚跟着地时刻HS. 实验采集的一个标准步态周期的小腿上矢状面角速度如图3所示, 分析在步态周期中关键特征点.

1) 脚跟离地时刻的特征. 脚跟离地时刻为站立阶段的终点， 理论上站立阶段矢状面的角速度为0， 当矢状面的角速度从0变成负时为脚跟离地时刻(按左手守则， 以逆时针方向为正). 由于测量时陀螺仪静止漂移等因素， 站立阶段的角速度往往不为零， 所以认为脚跟着地以后， 在一定时间之内矢状面角速度连续变小的点就是脚跟离地时刻.

2) 脚尖离地时刻的特征. 当脚跟离地后矢状面角速度达到负方向最大时(波谷)， 为脚尖离地时刻.

3)摆动阶段中点的特征. 摆动阶段中点有非常明显的特征， 即当脚尖完全离开地面进入摆动阶段时， 矢状面角速度经历一个由负到正的变化， 直至达到最大角速度(波峰)， 即为摆动阶段中点.

4) 脚跟着地时刻的特征. 从摆动阶段转变为脚跟着地时， 角速度会出现一个负的波谷， 所以在摆动中点后的第一个波谷为脚跟着地点， 完成一个步态周期， 并准备进入下一个步态周期阶段.

基于上述所示的步态周期矢状面角速度曲线中的关键特征点， 且为简化算法保证其在单片机中实时实现， 采用基于阈值的角速度信号步态分段算法进行步态周期分段. 其步态分段过程为：

1) 首先读取数据， 当N=0时， 系统将执行判断摆动阶段中点的子程序， 对于摆动阶段中点， 一开始先判断是否大于阈值λ1且为正的最大值(波峰)， 若满足此条件则判断为摆动阶段中点， 则N=1， 否则继续读取下一个数据.

2) 当N=1时， 系统将执行判断脚跟着地的子程序， 对于脚跟着地， 读取数据后， 判断此点是否为摆动阶段中点的第一个波谷， 若满足条件则判断为脚跟着地， 此时N=2， 否则继续读取数据.

3) 当N=2时， 系统将执行判断脚跟离地的子程序， 为了更容易识别这个点， 本算法中将脚跟着地后角速度绝对值开始变大且大于一定阈值， 而且前后一定时间内角速度值都递减的时刻作为脚跟离地点， 因此读取数据后先要判断：

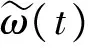
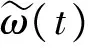
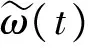
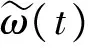
系统根据此算法一边进行数据采集， 一边进行步态分段， 既简单又具有较好的实时性， 且在单片机中易于实现.λ1、λ2、 Δt1和Δt2这四个阈值的具体取值将在下文中进一步讨论.

本研究所设计的足下垂功能性电刺激系统是通过识别脚跟离地HO和脚跟着地HS来分别控制功能性电刺激开启和停止， 对实时性要求比较高， 因此， 算法延时的长短将对电刺激的康复治疗效果有很大的影响. 从上面分析可以发现， 该算法识别脚跟着地HS没有滞后， 但识别脚跟离地HO存在Δt2的滞后. 本算法中， Δt2最长时间为120 ms， 加上电刺激信号在肌肉的传输延迟和肌肉本身的反应时间50～150 ms， 因此， 从算法检测到脚跟离地， 到胫前肌实际输出最大肌力的总时间为大约170～270 ms. 由于本系统主要设计用于足下垂患者康复治疗， 足下垂患者从脚跟离地HO到脚尖离地TO的推动阶段的时间要大于正常人的200 ms， 因此， 算法对功能性电刺激的开启时刻和停止时刻是恰当的， 可以满足足下垂患者功能性电刺激的要求.

3 算法识别结果

在Matlab软件上用步态分段算法识别步态周期的各个阶段， 即对穿戴于踝关节和小腿上的传感器在平地自由行走模式和跑步机平台下测得的角速度信号采用步态分段算法识别三个特征点： 脚跟离地(HO)、 摆动阶段中点(MS)、 脚跟着地(HS). 算法中λ1的取值范围是35～45 (°)·s-1，λ2的取值范围是-30～-20 (°)·s-1， 时间阈值Δt1的取值范围是80～90 ms， Δt2的取值范围是110～120 ms.

由于λ1的取值仅对摆动阶段中点的识别产生影响， 摆动阶段中点的识别有利于辅助脚跟着地和脚跟离地这两个时刻的识别， 因此有必要对λ1的取值进行分析， 找到最佳阈值. 对λ1取不同值时摆动阶段中点的识别率进行实验和统计， 实验中共采集8个志愿者在平地直线自由行走大约10 m和跑步机平台下行走15 s的步态数据， 每个志愿者在每个穿戴位置大概完成了36个步态周期， 统计结果如表1， 其中在小腿位置选取了三个不同的测试点.

表1 平地行走模式下摆动阶段中点的识别率

从表1统计结果可知，λ1取40 (°)·s-1时摆动阶段中点的识别率最高， 基本达到99.9%； 当λ1低于40 (°)·s-1时识别率相对较低， 这是由于脚跟离地后存在次波峰造成的误判； 当λ1高于40 (°)·s-1时的识别率也相对较低， 这是由于选择的阈值过大， 当行走的角速度幅值较小时系统识别不到造成的结果. 因此， 本算法选择λ1=40 (°)·s-1为最佳阈值.

对于λ2、 Δt1和Δt2这三个参数只对脚跟离地的识别产生影响， 而脚跟离地识别的准确性对功能性电刺激最佳刺激时相至关重要. 为了得到最佳识别率的阈值， 通过取8组不同λ2、 Δt1和Δt2取值组合， 将采集到的数据在Matlab软件上利用步态分段算法进行步态识别， 对平地自由行走模式下脚跟离地的识别结果进行统计， 如表2.

表2 平地行走模式下脚跟离地的识别率

从表2统计结果可知， 在三个参数各自对应的取值范围内，λ2的取值比Δt1、 Δt2的取值对脚跟离地识别率的影响更大， 当Δt1和Δt2值一定，λ2= -20 (°)·s-1时， 脚跟离地的识别率普遍比较低， 不会超过70%； 当λ2=-30 (°)·s-1时， 脚跟离地的识别率提高很多， 都超过了90%； 因此λ2值取-30 (°)·s-1时为最佳阈值. 当λ2和Δt1值一定， Δt2取120 ms时， 脚跟离地的识别率相较于Δt2取110 ms时更高， 为最佳阈值； 当λ2和Δt2值一定， Δt2取80 ms时， 脚跟离地的识别率相较于Δt2取90 ms时更高， 为最佳阈值. 综上分析可得， 取阈值λ2= -30 (°)·s-1、 Δt1=80 ms和Δt2=120 ms时， 对脚跟离地的识别率最高， 系统拥有较好的鲁棒性.

为进一步验证阈值取λ1=40 (°)·s-1、λ2=-30 (°)·s-1、 Δt1=80 ms和Δt2=120 ms是否在其他条件下也具有较高的识别率， 在平地自由行走模式和各种速度模式下对三个特征点： 脚跟离地(HO)、 摆动阶段中点(MS)和脚跟着地(HS)进行识别， 对脚跟离地和脚跟着地的识别率进行统计， 结果如表3和表4所示.

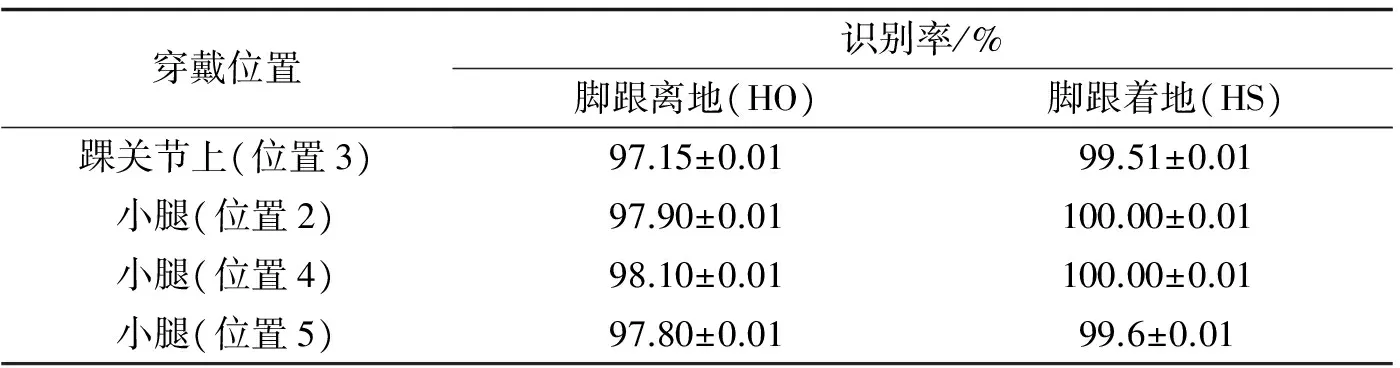
表3 平地自由行走模式下步态识别结果

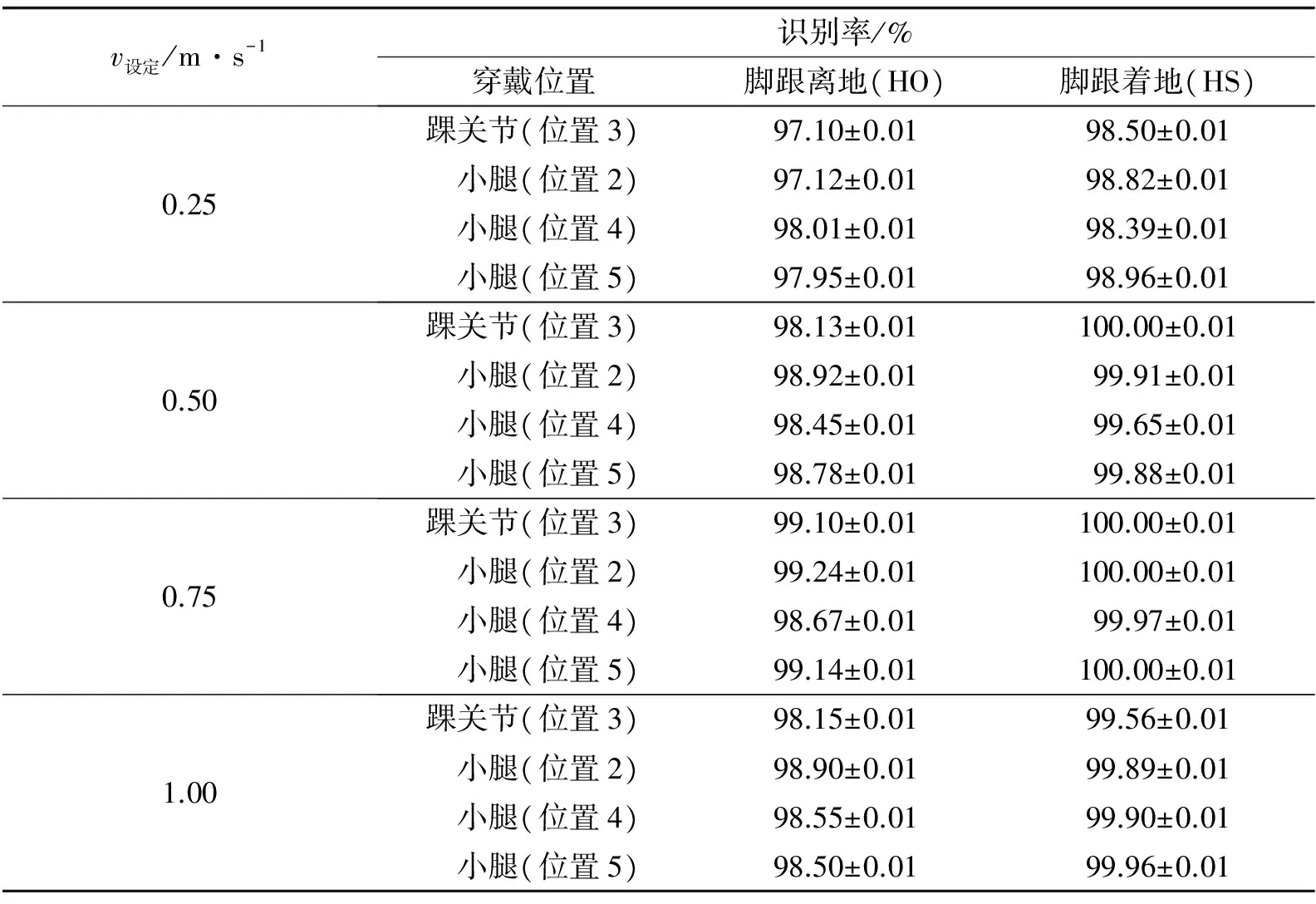
表4各种速度模式下步态识别结果

分析表3和表4统计结果可见， 在平地自由行走模式下， 对穿戴在踝关节和小腿上测得的角速度用步态分段算法识别脚跟离地和脚跟着地的识别率分别为97%和99%以上； 在各种速度模式下， 对穿戴在踝关节和小腿上测得的角速度用步态分段算法识别脚跟离地时刻和脚跟着地时刻的识别率分别为97%和98%以上. 结果表明， 该算法阈值取λ1=40 (°)·s-1、λ2=-30 (°)·s-1、 Δt1=80 ms和Δt2=120 ms时， 在平地自由行走模式和各种速度模式下均具有较高的识别率， 尤其对脚跟着地识别率几乎100%， 而脚跟离地识别率相对低一点. 这是由于脚要离地时容易晃动， 有多个次波谷， 而且每个人幅值有差异， 导致误判. 跑步机上设置最小速度采集时， 由于速度太慢， 实验者不易适应， 造成步态有些紊乱， 所以识别率也会稍低一点. 但总体而言本算法的识别率可达到97%～100%， 而文[8]中所提到的利用人步行时的径向和切向加速度数据进行离散分析的算法， 其识别率为84.2%～100%. 由此可看出, 本算法虽然简单， 但是依旧能够保持较好的识别率， 可以准确控制功能性电刺激输出.

另外， 算法对传感器穿戴在小腿和踝关节上采集到的角速度信号均能很好地识别， 所以小腿和踝关节均能作为传感器穿戴位置. 但考虑到传感器穿戴在踝关节时穿鞋容易受到限制， 而且对足下垂患者进行电刺激治疗的最佳刺激位置在小腿上， 将传感器穿戴在小腿能够使刺激位置和采集位置一体化， 穿戴更加方便和美观， 因此， 传感器穿戴在小腿上位置最佳.

4 结语

针对目前存在的步态分段方法识别率低、 实时性差、 过于复杂等缺点， 提出了基于角速度信号的功能性电刺激系统的步态分段算法， 用于识别步态周期的三个特殊点： 脚跟着地点、 脚跟离地点、 摆动阶段的中点. 当检测到脚跟离地时， 输出电刺激信号刺激患者胫前肌肉， 当检测到脚跟着地时停止电刺激， 以此来治疗足下垂. 该算法识别率高、 实时性好、 容易实现， 在足下垂治疗领域具有一定的应用价值.

参考文献：

[1] 许林海， 韩丽雅．功能强化训练结合肌电生物反馈对急性脑卒中患者上肢功能的影响[J]．中国康复， 2015(3)： 185-188．

[2] MONAGHAN C C, RIEL W J B M V, VELTINK P H. Control of triceps surae stimulation based on shank orientation using a uniaxial gyroscope during gait[J]. Medical & Biological Engineering & Computing, 2009, 47(11): 1181-1188.

[3] ZDRAGKAS G I, AVARITSIOTIS J N. Gait analysis and automatic gait event identification using accelerometers[C]//IEEE International Conference on Bioinformatics and Bioengineering. Athens: IEEE, 2008: 1-6.

[4] CHEN Y L, SHIH Y Y, CHEN W L,etal． Clincal evaluation of the tilt sensors feedback controlled FES for hemiplegia[C]//Proceedings of the 26th IEEE Annual International Conference on the EMBS. San Francisco: IEEE, 2004: 4737-4740．

[5] GOUWANDA D, SENANAYAKE S M N A. Application of hybrid multi-resolution wavelet decomposition method in detecting human walking gait events[C]//International Conference of Soft Computing and Pattern Recognition. Malacca: IEEE, 2009: 580-585.

[6] 韩宁. 基于体感网的步态分析算法的研究[D]. 大连： 大连理工大学, 2013.

[7] WANG Z L, QIU S, CAO Z L,etal. Quantitative assessment of dual gait analysis based on inertial sensors with body sensor network[J]. Sensor Review, 2013, 33(1): 48-56.

[8] RUETERBORIES J, SPAICH E G, ANDERSEN O K. Gait event detection for use in FES rehabilitation by radial and tangential foot accelerations[J]. Medical Engineering & Physics, 2014, 36(4): 502-508.

[9] 王桂茂, 严隽陶, 刘玉超, 等. 脑卒中偏瘫步态的时空参数与骨盆运动学分析[J]. 中国康复医学杂志, 2010, 25(12): 1148-1151.

[10] KOTIADIS D, HERMENS H J, VELTINK P H. Inertial gait phase detection for control of a drop foot stimulator inertial sensing for gait phase detection[J]. Medical Engineering & Physics, 2010, 32(4): 287-297.

[11] 谭志梅, 姜文文, 燕铁斌. 多通道功能性电刺激及其在脑卒中偏瘫侧肢体康复中的应用[J]. 中华物理医学与康复杂志, 2011, 33(6): 464-467.

[12] 马长波． 基于电机辅助功能性电刺激脚踏车康复训练系统的研究[D]． 哈尔滨： 哈尔滨工业大学， 2010．

[13] 黄金兰, 李玉榕, 陈建国. 基于微电子机械系统传感器的功能性电刺激系统[J]. 生物医学工程研究, 2015, 34(4):207-211.

[14] TIEN I, GLASER S D, BAJCSY R,etal. Results of using a wireless inertial measurirlg system to quantify gait motions in control subjects[J]. IEEE Transactions on Information Technology in Biomedicine, 2010, 14(4): 904-915.

[15] 侯季健. 人体步态信息采集系统设计[D]. 大连： 大连理工大学, 2015.

[16] GOUWANDA D, GOPALAI A A. A robust real-time gait event detection using wireless gyroscope and its application on normal and altered gaits[J]. Medical Engineering & Physics, 2015, 37(2): 219-225.