一种基于优化粒子滤波的锂电池SOC估计算法

吴兰花， 杨秀芝， 郑明魁， 苏凯雄

(福州大学物理与信息工程学院， 福建 福州 350116)

0 引言

电池SOC的定义为： 电池剩余容量与标称容量的比值[1]. 其准确估计能有效提高电池的利用率还能起到保护电池的作用. 锂电池是一个复杂的非线性的系统， 而电池SOC不仅无法直接测量得到， 而且受到诸如放电倍率、 工作温度、 循环寿命、 自放电等多种因素的影响. 因此， 锂电池SOC的准确估计是电池管理系统的重点与难点. 为此， 大量的学者对其进行了研究， 并提出多种估计方法， 如安时积分法[2]、 神经网络法[3]、 卡尔曼滤波法[4-6]、 以及粒子滤波法[7-9], 等. 其中， 粒子滤波(PF)算法可以弥补上述卡尔曼滤波算法的不足. 文献[7]利用PF算法实现锂电池SOC 与SOH的联合估计; 文献[8]提出一种基于温度补偿的锂电池模型， 然后应用双重PF算法实现SOC和漂移电流的同步估计； 文献[9]采用PF算法实现磷酸铁锂电池SOC估计， 结果表明PF算法对SOC 估计具有一定的适用性， 而且相较于EKF可以获得更加准确的估计. PF算法通过重要性重采样技术将注意力集中在权值较大的粒子上， 减小权值较小的粒子数. 但是， 较大权值的粒子被多次选择， 采样结果包含了许多重复点， 也会损失样本粒子多样性.

为了有效解决PF算法中粒子多样性丧失的问题， 本研究以某公司提供的磷酸铁锂电池放电数据为研究基础， 提出了基于改进粒子滤波的锂电池SOC估计算法. 在PF算法重采样之前增加基于BP神经网络的权值调整过程， 通过增大位于概率分布尾部的粒子权值， 提高样本粒子的多样性， 减小SOC估计误差.

1 锂电池状态空间模型的建立与参数辨识

实现电池SOC估计之前， 首先要建立合适的电池状态空间模型. 将SOC作为电池模型中的状态变量， 根据安时积分法中SOC 的计算原理并离散化得到锂电池的状态方程， 如下式所示

(1)

其中:xk为k时刻电池SOC状态值；ik表示k时刻电池放电电流；Cn为电池的标称容量； 电池的库伦效率为ηc=1； Δt为采样间隔；wk表示系统的过程噪声且wk～(0,Qw).

常见的电池简化电化学模型有Shepherd模型、 Unnewehr统一模型、 Nernst模型， 但这三种模型都只在局部较好地匹配电池SOC与开路电压的特性. 而由这三个模型组合而成的组合模型(CM)[10]能在锂电池整个充放电区间内提供较好拟合度. 因此， 本研究选择CM模型作为锂电池系统模型的观测方程， 其形式如下式所示，

(2)

其中:yk为k时刻电池端电压；E0表示电池SOC=100%时的电动势；R为电池内阻；K1、K2、K3、K4为模型匹配系数；vk表示系统观测噪声且vk～(0,Qv).

式(1)与式(2)共同构成锂电池的非线性状态空间模型. 式(2)的若干未知参数， 可根据一系列输入输出三元组{yk,ik,xk}， 采用最小二乘估计法实现参数的离线辨识.

2 粒子滤波概述

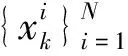
已知锂电池非线性系统状态空间模型如式(1)、 (2)所示， PF算法[8]可以归纳为以下几个步骤：

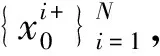
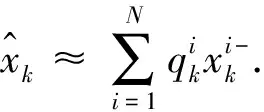
3 基于BP神经网络的改进粒子滤波

3.1 BP神经网络调整粒子权值

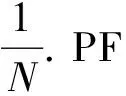
本研究提出的基于改进粒子滤波的SOC估计算法， 在PF算法重采样之前增加了权值调整过程， 利用BP 神经网络来调整位于概率尾部的低权值粒子， 使其进入高权值区域， 同时部分高权值的粒子在一定情况下会分裂成两个较小权值粒子， 从而达到提高样本粒子多样性的目的.

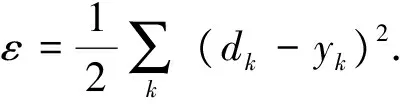
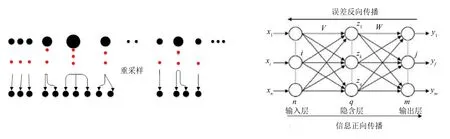
图1 粒子滤波重采样示意图

本算法在重采样之前增加了两个步骤： 第一步是权值分裂. 在计算得到粒子权值之后， 设定一个阈值并以此为界将权值较大的q粒子分裂成两个权值减半的粒子. 为保证粒子总数不变， 舍弃权值最小的q个粒子. 第二步是采用BP神经网络调整那些低权值粒子. 首先进行网络训练， 将粒子的状态值作为神经网络的输入， 该时刻的系统量测值作为神经网络的教师信号， 通过神经网络多次锻炼， 将误差反传， 得到具有系统量测方程功能的神经网络模型. 然后将需要调整的小权值粒子的状态值作为神经网络的输入数据， 并将网络的输出值作用于权值公式得到粒子的新权值. 通过这个步骤可以使粒子的平均值更接近于真实状态， 减小粒子采样的方差， 达到提高粒子多样性， 改善滤波性能的目的.

3.2 基于BP 神经网络的改进粒子滤波算法实现

图3 本算法流程图Fig.3 Algorithm processes

图3是本研究提出的改进算法的实现流程图， 算法流程分析如下.

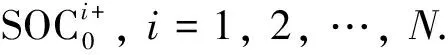
步骤二： 对于k=1， 2， …，N.

2) 粒子权值更新.

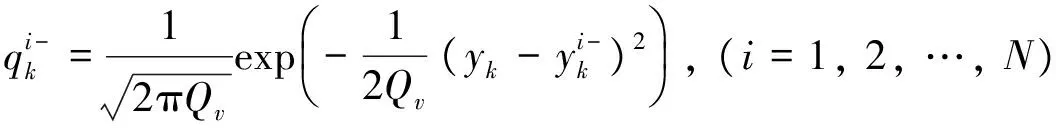
3)权值分裂. 将粒子权值降序排列， 以某阈值为界， 将权值较大的q个粒子分裂成两个权值减半的粒子， 并舍弃粒子矩阵中权值靠后的q个粒子.

4 实验分析

在采集了大量实测电池数据的基础上， 实现本算法以及文献[9]所述PF算法进行SOC预测， 并将两种算法的预测结果与SOC实测值相比较. 由于本研究的锂电池是作通信领域备用电源使用的磷酸铁锂电池， 其运行环境温度被控制在较为稳定的状态. 因此， 选取的实验数据为某公司提供的磷酸铁锂电池室温(25 ℃)工作条件下， 放电倍率(放电倍率等于电池额定容量的倍数)分别为1C、 0.5C、 0.2C三组放电测试数据. 每组数据的采样间隔都是60 s， 取粒子数N=200， 状态噪声方差Qw=1， 观测噪声方差Qv=10. 本实验使用SOC估计相对误差(相对误差=估计值-实测值)的绝对值来刻画算法的估计性能. 经过多次测试并调整得到的SOC估计结果分别如图4～6所示.

图4 1C放电情况下的SOC估计结果Fig.4 SOC estimate results under 1C discharge

图5 0.5C放电情况下的SOC估计结果Fig.5 SOC estimate results under 0.5C discharge

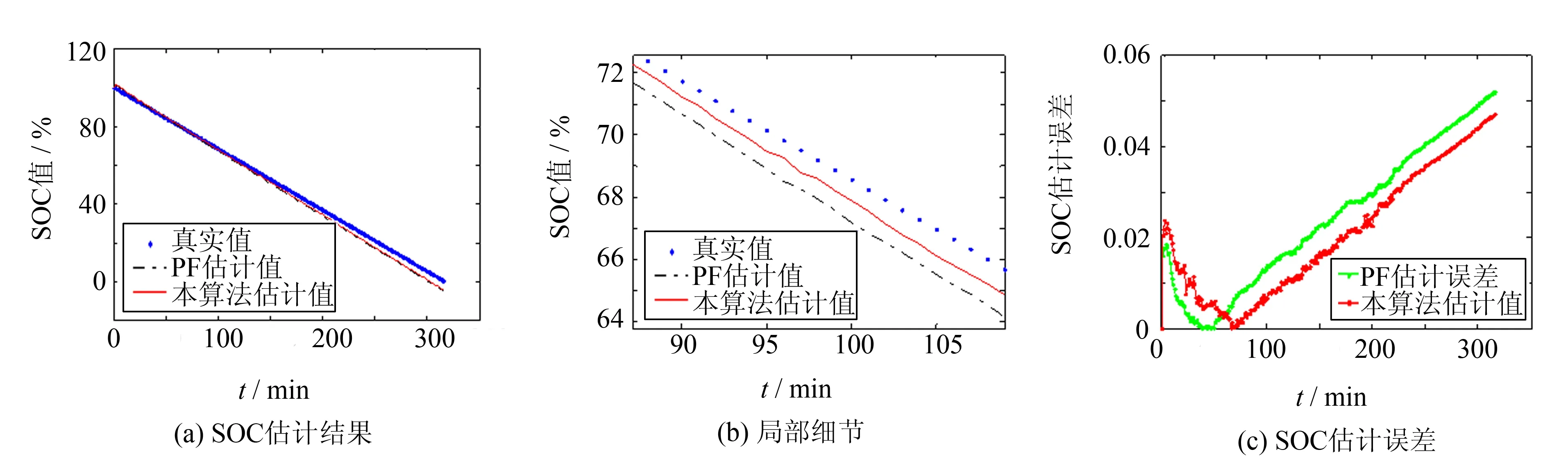
图6 0.2C放电情况下的SOC估计结果Fig.6 SOC estimate results under 0.2C discharge

图4 显示了电池以1C放电倍率恒流放电的条件下， 本算法及PF算法的估计情况. 其中， 图4(a)为一个完整放电区间内， SOC估计值与实测值的对比图. 从图中可以看到用算法得到的SOC 估计值曲线与实测值非常相近， 说明PF 算法和本算法都能对电池SOC 做出较好的估计； 图4(b)展示了算法估计结果的局部细节， 可以看到本算法的估计值更加接近实测值， 说明相比于PF 算法， 本算法可以获得更高的估计精度； 两种算法的误差如图4(c)所示， 从图中可以看到， 本算法的估计误差小于PF 算法， 进一步说明了本算法的估计性能优于PF算法.

在0.5C恒流放电的情况下， PF 算法及本算法的估计情况如图5 所示. 图5(a)显示了两种算法的整体估计性能， 图中本算法和PF算法都能较好实现SOC准确估计， 在电池放电末期由于电池迟滞特性的作用， 算法的估计误差增大； 从图5(b)中可以看到， 本算法的估计值更加接近实测值， 而且两种算法的估计误差总体呈现先减小后增大的趋势， 这是因为在算法估计初始阶段， 粒子存在初始误差， 随着多次递推计算， 这种误差逐渐缩小， 算法估计值快速收敛于实测值. 而随着放电时间的增加， 尤其是在电池放电后期， 电池的迟滞特性显著， 迟滞特性成为影响SOC估计精度的主要因素. 进一步观察两种算法的估计误差可以看到： 在放电初期， PF算法的误差小于本算法， 但是这段时间很短， 只占整个放电周期的15%左右. 随着放电时间的增加， 本研究算法很快就体现出优势， 粒子权值调整过程有效地提高了粒子多样性， 减小了粒子采样方差， 从而提高了SOC估计精度， 使得算法的估计误差曲线小于PF算法. 因此， 相比于PF算法， 虽然在放电初期本算法的误差收敛速度没有PF算法快， 但从电池的整体放电情况来看， 绝大部分时间里， 本算法的估计误差都小于PF算法， 所获得的估计曲线更加接近SOC真实值， 估计性能更好.

为了验证电池在小倍率放电情况下， 算法的SOC估计特性， 本研究进一步对0.2C放电倍率下的电池SOC 进行估计， 测试结果如图6所示. 从图6 中可以发现， 在这种放电情况下算法的估计性能结果与图5类似. 从整体来看， 两种算法都能较为准确地实现SOC估计， 随着放电时间的增加， 尤其是放电末期， 由于电池迟滞作用的影响， 算法估计误差总体呈现先减小后增大的趋势. 在放电初期的短时间内， 本算法对粒子初始误差具有负作用， PF算法表现出更好的初始误差收敛效果. 但随着放电时间的增加， 在绝大多部分的放电时间内， 本算法得到的估计误差均小于PF算法， 所获得的SOC估计值更加接近真实值， 本算法具有更好的估计性能.

为了更直观地对比算法的SOC估计性能， 从统计学角度出发， 分别计算了两种算法的均方根误差及最大绝对误差. SOC估计的均方根误差(RMSE)定义为：

表1滤波性能

Tab.1Filterperformance(%)

算法1C放电MAERMSE0．5C放电MAERMSE0．2C放电MAERMSEPF算法[9]1．5681．3524．02212．36735．20362．8786本算法1．12150．860133．52211．99774．70972．4932

由表1知， 在不同放电倍率下， 本算法的RMSE比PF算法的SOC估计RMSE均有不同程度的改善. 继续对比三种放电情况下SOC估计的MAE可以看到， 在相同条件下本算法得到的MAE也均小于PF算法， 进一步说明了本算法具有更优异的SOC估计性能. 结合表中统计值还可以看出， 不同放电倍率情况下本算法的性能改善的程度有所不同， 大倍率放电时得到的统计值较小， 本算法的性能改善程度也更高. 根据表1的数值对比结果可以看出， 本算法在SOC估计的RMSE和MAE两方面都有显著的改善， 进一步验证了本算法比PF算法具有更好SOC估计性能.

5 结语

针对SOC估计中PF算法引入重采样技术后权值较大的粒子会被多次采样， 粒子多样性丧失的问题. 本研究在建立锂电池状态空间模型后， 提出一种基于改进粒子滤波的锂电池SOC估计算法. 本算法在PF算法的基础上， 将BP神经网络引入到PF算法的权值更新过程中， 增大位于概率分布尾部的粒子权值， 使其进入高权值区域， 减小粒子采样方差， 提高粒子的多样性. 结果表明， 从整个放电过程来看， 本算法的SOC估计更加接近真实值， 大部分情况下其估计误差也明显小于PF算法. 结合计算所得的误差数值结果， 本算法在SOC估计的RMSE和MAE两方面都有显著的改善. 因此， 与PF算法相比， 本算法具有更好的SOC估计性能.

参考文献：

[1] PILLER S， PERRIN M， JOSSEN A. Methods for state-of-charge determination and their applications[J]. Journal of Power Sources， 2001， 96(1): 113-120.

[2] 林成涛， 王军平， 陈全世. 电动汽车SOC估计方法原理与应用[J]. 电池， 2004， 34(5): 376-378.

[3] WEIGERT T， TIAN Q， LIAN K. State-of-charge prediction of batteries and battery-supercapacitor hybrids using artificial neural networks[J]. Journal of Power Sources， 2011， 196(8): 4061-4066.

[4] PLETT G L. Extended kalman filtering for battery management systems of LiPB-based HEV battery packs: part 1. background[J]. Journal of Power Sources， 2004， 134(2): 252-261.

[5] CHARKHGARD M， FARROKHI M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF[J]. IEEE Transactions on Industrial Electronics， 2010， 57(12): 4178-4187.

[6] 何耀， 刘兴涛， 陈立， 等. 基于无迹卡尔曼粒子滤波算法的动力锂电池SOC估计[C]// 第14届中国系统仿真技术及其应用学术年会. 安徽： 中国科学技术大学出版社， 2012： 884-888.

[7] SCHWUNK S， ARMBRUSTER N， STRAUB S，etal. Particle filter for state of charge and state of health estimation for lithium-iron phosphate batteries[J]. Journal of Power Sources， 2013， 239(10): 705-710.

[8] LIU X， CHEN Z， ZHANG C，etal. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation[J]. Applied Energy， 2014， 123(3): 263-272.

[9] WANG Y， ZHANG C， CHEN Z. A method for joint estimation of state-of-charge and available energy of LiFePO4， batteries[J]. Applied Energy， 2014， 135(C): 81-87.

[10] PLETT G L. Extended kalman filtering for battery management systems of LiPB-based HEV battery packs: part 2. modeling and identification[J]. Journal of Power Sources， 2004， 134(2): 262-276.

[11] QIN W， PENG Q. An improved particle filter algorithm based on neural network for visual tracking[C]//International Conference on Communications， Circuits and Systems. [S.l.]: IEEE， 2007: 765-768.