不同接触下镜片亚表面损伤形成数值模拟
卢剑波, 高诚辉, 任志英, 江 伟
(1. 福州大学机械工程及自动化学院, 福建 福州 350116; 2. 福建福光股份有限公司, 福建 福州 350004)
0 引言
随着现代科学技术的飞速发展, 光学技术领域探索不断深入, 光学镜片得到了广泛应用, 遍及人们日常生活的各个方面, 需求大量增长, 且技术要求较传统的光学元件也有很大提升. 为此, 光学镜片超精密磨削加工技术应运而生, 其不但加工效率高, 磨削表面质量与传统的磨削、 研磨和抛光等加工技术相比也更加可观[1]. 但是光学镜片通常为硬脆性材料, 具有极高的硬度和脆性、 较低的断裂韧性, 在加工过程中极易产生位错、 微裂纹和微断裂等亚表面损伤, 难以获得较高的表面质量和面型精度, 严重影响光学镜片的光学性能指标[2]. 因此, 研究光学镜片的超精密磨削机理, 探究和控制光学镜片亚表面裂纹的形成和扩展, 对于获得高质量的光学镜片表面具有指导作用.
当前关于光学镜片亚表面损伤形成和扩展的研究大部分都是通过实验手段来实现, 而实际加工中产生的瞬态应力、 应变和磨削温度等数据难以进行在线检测, 仅仅依靠实验方法很难精确地抑制亚表面损伤的扩展. 有限元仿真不但可操作性强, 研究成本较低, 重复性高, 而且可以深入揭示实验方法难以获得的物理力学现象, 实现对光学镜片亚表面损伤结果的预测和控制, 从而在工程实际中指导磨削加工参数的设计. 但是学者们在光学镜片亚表面损伤的仿真研究中, 往往仅关注加工工艺参数, 如砂轮进给速度、 砂轮线速度和磨削深度等参数对亚表面损伤的影响, 而忽视了磨削过程中磨粒形状及其与光学镜片粗糙表面间的接触状态对亚表面损伤的影响, 通常将粗糙平面假设为理想平面, 将磨粒视为球体或圆锥体等规则磨粒, 对磨粒与光学镜片间的接触模型过于简化, 使仿真结果与工程实际间存在误差. 因此, 本研究从有限元仿真角度对单颗金刚石磨粒磨削光学镜片进行数值模拟, 充分考虑不规则磨粒与光学镜片粗糙表面之间不同的接触状态, 并总结国内外学者的研究成果, 将磨粒与光学镜片的接触状态归纳为单点接触、 直线接触和弧线接触, 分别建立了单颗磨粒与光学镜片间的双微凸体接触模型, 分析不规则磨粒与光学镜片粗糙表面在不同接触状态下对光学镜片亚表面损伤形成和扩展的影响规律, 有助于更好地理解超精密磨削光学镜片的加工机理, 并指导实际磨削加工过程.
1 有限元模型
1.1 机理分析
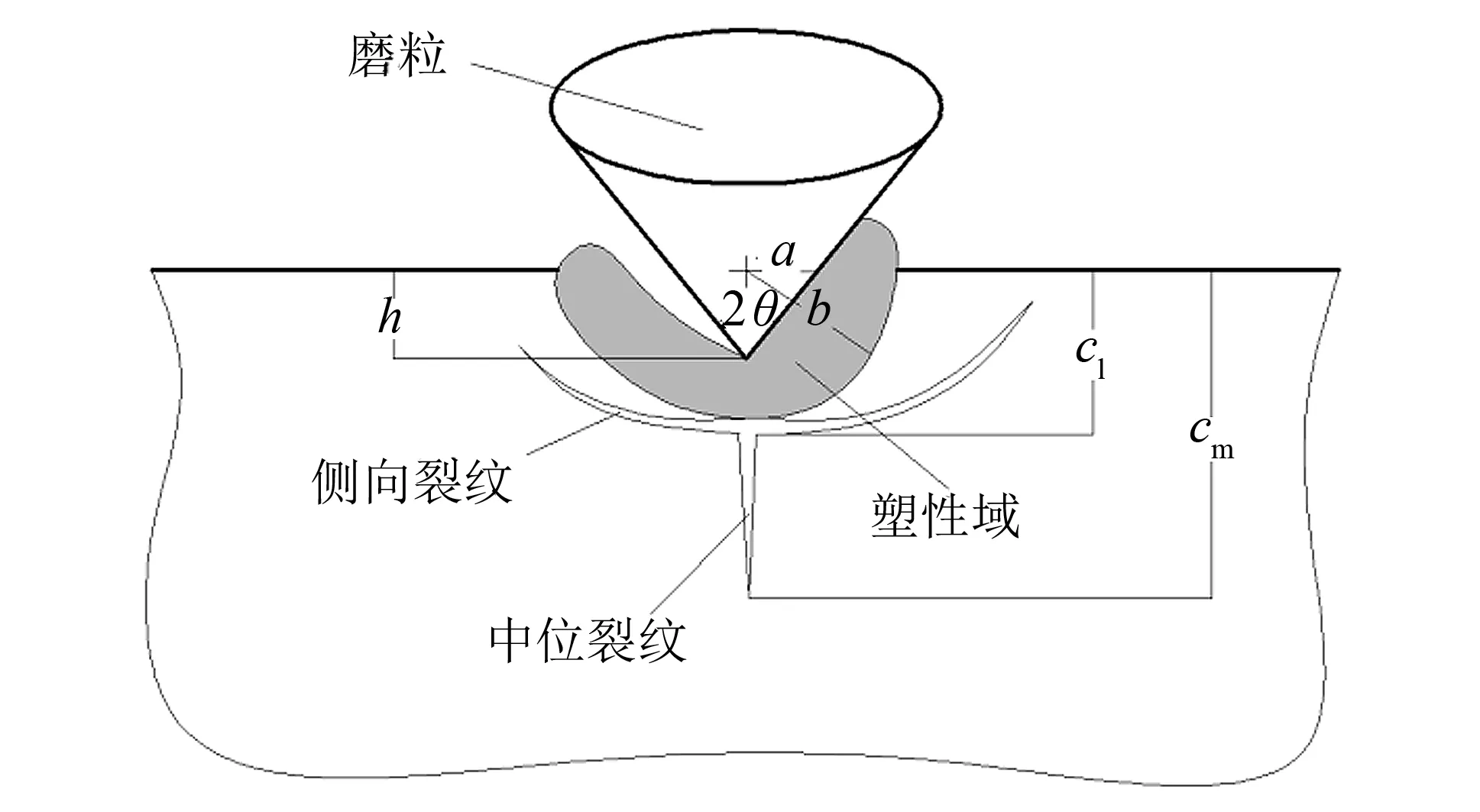
图1 印压作用下裂纹分布示意图Fig.1 Crack distribution under pressure
光学镜片等硬脆性材料的亚表面损伤是指由于磨削和切削等机械加工过程在工件近表面区域产生的微观裂纹、 塑性变形、 空穴和污染等内部损伤[3]. 为研究硬脆性材料进行机械加工导致表面层损伤的机理, 多数学者常采用基于压痕断裂力学理论的压痕试验来研究硬脆性材料的接触损伤、 塑性变形和断裂韧性[4]. Evans和Lawn等[5-6]在对裂纹损伤研究中提出, 可以使用中位裂纹和侧向裂纹对尖锐压头的印压和划擦所产生的亚表面损伤进行描述, 如图1所示. 在磨粒的印压作用下, 工件在压头下方区域会发生脆塑转变, 形成塑性变形域; 随着载荷的不断增大, 塑性域外围会逐渐产生微裂纹, 并沿塑性域下方向内部不断扩展合并形成的中位裂纹; 而当进行卸载时, 微裂纹则沿塑性域两侧向表面扩展合并形成的侧向裂纹.
李圣怡等[7]基于压痕断裂力学和前人的研究成果, 引入考虑压痕应力场弹性组元的修整系数κ(取值为2.23), 优化了中位裂纹深度和侧向裂纹深度的理论计算公式, 并假设中位裂纹深度为亚表面裂纹深度, 其计算公式为:
(1)
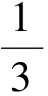
(2)
压入硬度H是表示压入过程中材料抵抗变形的能力[8], 以圆锥形磨粒为例, 可表示为:
(3)
a=h·tanθ
(4)
式中:AN为压头与试样接触区域沿竖直方向的投影面积;a为压入残余宽度的一半;h是压入残余深度, 如图1所示; 参数q为常数, 其取值范围为1≤q≤2, 因此压入硬度可整理为:
(5)
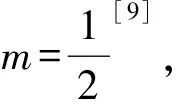
(6)
由于光学玻璃磨削过程中的侧向裂纹一般从塑性变形域的底部开始成形, 并沿与工件表面几乎平行的方向横向扩展, 如图1所示. 因此, 通常认为侧向裂纹深度等同于塑性变形域的半径[10], 即:
cl=b
(7)
Jing 等[11]通过理论和试验相合, 得出塑性变形域半径的显式表达式为:
(8)
式中:σy为屈服应力,ν为泊松比. 以圆锥形磨粒为例, 侧向裂纹深度可表示为:
(9)
由公式(6)和公式(9)可知, 在相同的磨削加工条件下, 光学镜片的中位裂纹深度和侧位裂纹深度受压入残余深度和磨粒锐度角的影响较大. 不同磨粒形状具有不同的磨粒锐度角, 同时磨粒与光学镜片粗糙表面间不同的接触状态直接决定磨粒的压入残余深度. 因此, 在进行有限元仿真研究过程中, 对磨粒过于简化, 忽视磨粒对光学亚表面损伤的影响势必使仿真结果与实际结果不相符. 对不规则磨粒与光学镜片粗糙表面间不同接触状态进行仿真研究, 建立更加接近实际磨削工况的双微凸体接触模型, 分析其对光学镜片亚表面损伤的影响具有十分重要的工程意义, 有助于更好地理解光学镜片超精密加工机理.
1.2 不规则磨粒模型的建立
采用非线性有限元软件ABAQUS建立单颗金刚石磨粒与BK7光学玻璃粗糙表面间的二维接触模型, 分析各种不同形状的磨粒与光学镜片间的不同接触状态对其亚表面损伤的影响.
在实际磨削加工中, 磨粒往往具有不规则的几何形状, 常见的有球体、 圆锥体、 立方体、 八面体及其解理形成的四面体等[12]. 同时, 磨粒在砂轮上的粘附情况也各不相同, 不同粘附方式其磨削能力也不同. 以立方体磨粒为例, 单颗磨粒与光学镜片表面接触时, 虽然刚开始进入接触状态时为点接触, 但是由于磨粒下方区域光学镜片受压力作用发生的脆塑转变行为形成塑性加工域, 且磨粒在砂轮上是随机粘附的, 因此, 磨削加工过程中磨粒与工件表面间的接触状态可能是点接触, 也可能是线接触, 甚至是面接触. 磨削加工过程中不同的接触状态对亚表面损伤的影响各不相同, 而且加工材料表面去除率也不同, 对磨削表面加工质量和加工效率都具有一定的影响. 因此, 总结不同形状磨粒与工件表面的不同接触状态, 将单颗磨粒与光学镜片粗糙表面的接触状态归纳为点接触、 线接触和弧接触等三种接触状态分别建立二维接触模型.

图2 磨粒模型图Fig.2 Abrasive model
在模型仿真参数的设置上, 沿磨粒磨削方向对磨粒施加5 m·s-1的恒定磨削速度, 同时对磨粒施加垂直向下的恒定法向载荷300 μN, 磨粒与工件的摩擦系数设为0.3. 选用粒径为100 μm的金刚石磨粒进行仿真, 其密度为3.5 g·cm-3, 弹性模量为1.1 TPa, 泊松比为0.07. 由于金刚石的硬度和强度远大于BK7光学玻璃, 在磨削加工过程中基本不发生形变, 为减少计算时间, 建模时假设金刚石磨粒为刚体, 对其进行刚体约束.
各磨粒模型如图2所示, 利用三角形网格对其进行自由网格划分, 网格类型为3节点线性平面应力三角形单元CPS3.
1.3 光学玻璃粗糙表面的建立
为使模拟结果更接近真实工况, 需要对具有多尺度性和随机性特点的光学工件的表面形貌进行合理的建模. 目前, 分形几何理论被大多学者接受并用于表征零件粗糙表面的几何形貌. 采用二维W-M函数法[13]建立粗糙表面, 其表达式[14-15]为:
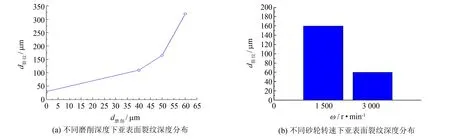
式中:z(x,y)为随机表面轮廓的高度;La为取样长度;G为尺度系数;D为分形维数(2 由式(10)可知, W-M函数法建立的分形粗糙表面主要取决于分形维数D和尺度系数G.D用于控制材料微观形貌的轮廓密集度,D越大说明工件表面细节越丰富,G用于控制材料的微观形貌的上下波动, 在建模过程中对D和G进行适当的取值, 即可模拟出接近实际的光学表面形貌.D和G可通过W-M的功率谱变换估计得到[16]. 根据实验测量以及基于表面平整度和频率分布密度的考虑, 选取参数D=2.4,γ=1.5,G=2 μm, 利用Matlab软件进行程序编写并生成随机分形粗糙表面, 再导入Pro/E软件建立三维粗糙表面实体, 最终生成光学镜片的三维粗糙表面模型. 考虑到三维仿真模型计算量过大且不易直观地对仿真结果进行在线观测, 因此建立了二维的接触仿真模型. 同时, 为排除单个二维粗糙表面的偶然性对仿真结果造成影响, 在所建立的光学镜片实体上随机选择3个横截面生成二维粗糙表面, 并分别研究3个截面上进行单程磨削时, 该二维粗糙表面与不规则磨粒接触存在的三种不同接触状态对光学镜片亚表面损伤的影响. 选择光学玻璃BK7进行仿真, 其密度为2.51 g·cm-3, 弹性模量为81 GPa, 泊松比为0.208. 在设置破坏机制时, 采用了ABAQUS中更适合光学玻璃的Brittle Cracking准则进行模拟. 在进行网格划分时, 采用的网格类型为CPS3, 选择三角形网格进行自由网格划分, 并在接触区域进行相应的网格细分. 同时, 由于在实际磨削加工中, 光学镜片的自转速度远小于砂轮线速度, 因此假设光学镜片固定不动, 对其底部和左右两侧面施加所有方向自由度的约束. 本研究旨在探索磨削加工过程中, 不规则磨粒与光学镜片间不同的接触状态对光学镜片亚表面损伤的影响规律. 因此, 在设计仿真方案时, 制定了在相同的加工工艺参数作用下, 随机选择光学玻璃上同一截面的单程磨削过程中磨粒与光学镜片的三种不同接触状态进行模拟仿真, 研究不同接触状态与光学镜片的亚表面裂纹深度和材料去除率间的关系. 单颗磨粒与光学镜片粗糙表面微凸体的接触过程是一个由于应力的加载和卸载产生表面材料去除并造成亚表面损伤形成和扩展的动态过程, 以截面1上的单程磨削为例, 三种不同接触状态的动态接触过程如图3到图7所示. 图3所示磨粒与工件表面微凸体均尚未接触, 粗糙表面保持良好, 磨粒在砂轮的作用下向右运动. 图3 未接触表面形貌图Fig.3 Non-contact surface topography 图4所示为工件表面微凸体刚开始受到磨粒冲击时的表面形貌图, 由于光学玻璃的硬脆性, 且瞬间冲击应力过大, 微凸体在应力冲击下直接破碎并被去除, 在接触区周围产生大量无序随机分布的微裂纹. 从图中可以看出, 初始接触时点接触产生的接触应力最大, 达到26.730 GPa, 线接触产生的接触应力为4.224 GPa, 弧接触产生的接触应力最小, 仅为2.931 GPa. 这是由于磨粒与粗糙表面微凸体接触时, 点接触的接触面积较小, 而弧接触的接触面积较大. 图4 初始接触表面形貌图Fig.4 Initial contact surface topography 图5所示为随着磨粒继续运动, 磨粒与工件表面微凸体完成接触, 此时应力逐渐加载并以接触区域为圆心呈圆弧形扩散到工件基体中, 呈现出如图所示的应力环并产生应力集中. 同时微裂纹逐渐发展, 变长变宽合并形成了中位裂纹和侧位裂纹分布的初始形貌. 图5 应力加载时表面形貌图Fig. 5 Surface topography at stress loading 图6所示为随着应力卸载时的表面形貌图. 从图中可知, 此时裂纹扩展速度大大降低, 并趋于稳定, 形成了以中位裂纹和侧位裂纹为主, 若干随机微裂纹为辅的亚表面裂纹分布情况. 同时, 三种接触状态的最大应力点均位于工件粗糙表面, 这是由于应力已扩展并分散至工件内部深处, 而工件表面由于崎岖不平而产生应力集中, 因此此时最大应力出现于工件表面. 另外, 从图中还可以看出, 与磨粒接触的微凸体相邻的左右两侧的微凸体均产生了一定的应力集中, 且右侧微凸体内部的应力大小和区域均大于左侧微凸体的应力, 同时以接触微凸体为圆心, 相邻两个微凸体为端点, 应力包络形成一个内应力环, 其大小和深度均小于外部的主应力环, 这是由于材料内部组织结构、 载荷状况和裂纹扩展情况共同决定的. 图6 应力卸载时表面形貌图Fig.6 Surface topography when stress is unloaded 图7所示为应力基本完成卸载, 且裂纹完全扩展, 形成明显的中位裂纹和侧向裂纹的分布情况. 其中, 中位裂纹向粗糙表面微凸体内部扩展, 它是光学玻璃亚表面损伤的主要形式; 侧位裂纹则延伸至工件表面, 并最终造成材料的去除. 从图中也可以明显看出, 弧接触状态造成的材料去除最多, 形成的亚表面裂纹深度也最大, 而线接触状态造成的的材料去除最少, 形成的亚表面裂纹深度也最小. 图7 加工完成时亚表面损伤形貌图Fig.7 Sub-surface damage morphology when machining is completed 以亚表面裂纹深度为主要指标表征光学镜片的亚表面损伤, 用表面材料去除率来判断磨削的加工效率, 从而仿真研究在相同的砂轮线速度和磨削加工深度等工艺参数作用下, 单颗磨粒与光学镜片接触的三种不同状态对光学镜片磨削加工表面质量和加工效率的影响. 图8 应力-时间关系变化曲线图Fig.8 Stress-time relationship change curve 由于亚表面损伤的形成和扩展是个连续的动态变化过程, 难以实时在线检测每个节点的应力变化, 因此选取截面1上单程磨削过程中磨粒与光学镜片微凸体接触的动态过程中最具有代表性的最大应力的变化来分析应力变化过程. 由于磨粒与微凸体接触瞬间应力过大, 影响图形整体视觉效果, 因此分别选取了三种不同磨粒与相同微凸体接触过程中0.04 μs的时间段内应力加载到卸载过程中出现的12个最大应力结点, 分析不同磨粒与微凸体动态接触过程中最大应力值随时间的变化关系, 如图8所示. 从图中可知, 三种磨粒与粗糙表面微凸体的接触应力均随时间变化而逐渐减少, 并且呈现出先快后慢的趋势, 同时应力在短时间内不会马上消失, 而是残留于工件内部, 随着时间的推移慢慢趋于零. 另外, 在相同的加工工艺条件下, 不规则磨粒与粗糙表面微凸体刚开始接触时, 由于点接触的接触面积最小, 因此产生的接触应力最大, 而弧接触的接触面积最大, 则接触应力最小. 并且, 当时间达到0.13 μs之后, 虽然扩展至工件内部的应力趋于稳定并继续逐渐减小, 但是由图中可以看出, 弧接触产生的应力始终大于其他两种接触状态下的应力, 线接触的应力始终最小, 这必然会使得弧接触所造成的亚表面裂纹扩展深度大于其他接触状态, 材料去除速率快于其他接触状态, 此结果将在后续研究中得以印证. 不同接触状态对亚表面裂纹深度的影响见图9所示, 以截面2为例, 通过对比光学镜片上相同位置处的单程磨削过程所形成的亚表面裂纹深度可知, 弧接触形成的亚表面裂纹深度最大, 点接触次之, 线接触最小. 其中, 弧接触的形成的亚表面裂纹深度为96.153 μm, 点接触为88.690 μm, 而线接触仅为79.835 μm. 由此可知, 若要提高光学镜片加工表面质量, 减小亚表层损伤, 磨削加工时应尽量使得磨粒与工件表面在线接触的状态下进行加工. 对磨削材料去除率的影响如图10所示, 以截面2为例, 三种不同的接触状态中, 弧接触在磨削加工过程的材料去除率最大, 达到了9.352×106μm3·s-1; 点接触次之; 线接触最小, 仅有5.772×106μm3·s-1. 因此, 在保证加工质量的情况下, 若要提高加工效率, 磨削时应选择球形磨粒较多的砂轮, 保证磨粒与工件更多地处于弧线接触的状态下进行加工. 图9 不同接触状态对亚表面裂纹深度的影响 通过上述数据分析并结合图7所示单颗不规则磨粒与粗糙表面间不同接触状态在同一接触区域的亚表面损伤形貌图, 可以直观地看出同一实体上3个不同截面的磨削加工过程中, 虽然每个截面的表面形貌各异, 但是磨粒与光学镜片粗糙表面三种不同接触状态中, 弧接触的材料去除率总是最高, 但是也形成了最大的亚表面裂纹深度, 加工表面质量较差; 线接触形成的亚表面裂纹深度总是最小, 但是材料去除率也最低, 去除效率较低. 因此, 在实际磨削加工过程中, 粗加工时应选择球形磨粒较多的砂轮进行磨削加工, 精加工时则应选择不规则的棱形磨粒较多的砂轮, 并及时修整. 孟彬彬等[17]通过在精密卧轴矩台平面磨床上搭建实验平台, 将单颗金刚石磨粒焊接于特定基体并将基体固定于砂轮上对K9光学玻璃进行磨削试验, 镜片处理后使用扫描电镜及激光共聚焦显微镜观察结果, 研究磨削过程对镜片亚表面损伤的影响. 该试验方案设计了几组不同的磨削深度和砂轮速度, 研究磨削过程中加工工艺参数对亚表面损伤的影响. 该试验方案选用K9光学玻璃进行磨削, 其材料参数与BK7光学玻璃基本一致, 选择金刚石磨粒, 与本研究相同. 其试验结果如图11所示, 从图中可知, 在加工工艺参数设置合理的情况下, 磨削过程中产生的光学镜片亚表面损伤深度为30~150 μm. 而从图9可知, 本研究仿真模型模拟得出的亚表面裂纹深度区间为40~100 μm, 处于合理的区间范围. 图11 工艺参数对亚表面损伤的影响Fig.11 Effect of different process parameters on sub-surface damage 由上述仿真结果和试验结果的对比分析可知, 所建立的单颗金刚石磨粒磨削加工光学镜片模型对预测单颗粒光学镜片磨削加工亚表面裂纹形貌和深度等亚表面损伤情况具有一定的合理性与正确性. 在此基础上, 分别研究单颗磨粒与光学镜片间三种不同接触状态对亚表面损伤的影响. 通过仿真分析发现, 所得的亚表面裂纹深度均处于试验结果范围内, 且弧接触状态产生的亚表面裂纹深度最大, 点接触次之, 线接触最小; 弧接触状态的材料去除率最高, 点接触次之, 线接触最小. 针对许多学者在进行光学玻璃超精密磨削仿真时对磨粒和光学镜片模型过于简化的现象, 总结了不规则磨粒与光学镜片粗糙表面间的三种不同接触状态, 并深入研究其对光学镜片亚表面损伤的影响, 从而更好地理解磨削加工机理, 指导实际磨削加工过程, 提高加工表面质量和加工效率. 1) 总结超精密磨削加工中的不规则磨粒与光学镜片粗糙表面间的三种不同接触状态, 并采用有限元软件建立磨粒与光学镜片粗糙表面双微凸体接触模型, 为深入研究光学玻璃磨削加工机理提供一定的参考. 2) 通过分析磨粒与微凸体在不同接触状态下的动态接触过程中最大应力值的变化, 得出应力随时间的推移逐渐减少并呈现出先快后慢的趋势. 同时, 初始接触时点接触产生的接触应力最大, 达到了26.730 GPa; 线接触较小, 接触应力为4.224 GPa; 弧接触产生的接触应力最小, 仅有2.931 GPa. 而当工件内部的应力趋于稳定并继续逐渐减小时, 弧接触产生的应力始终大于其他两种接触状态下的应力, 线接触的应力始终最小. 3) 分析不同接触状态对磨削表面质量和加工效率的影响, 其中弧接触形成的亚表面裂纹深度最大, 达到96.153 μm, 点接触次之, 线接触最小, 仅为79.835 μm, 说明线接触状态下造成的亚表面损伤最小, 磨削加工表面质量较高. 同时, 弧接触状态下的材料去除率最高, 达到9.352×106μm3·s-1, 点接触次之, 线接触最小, 仅为5.772×106μm3·s-1, 说明弧接触状态下的磨削加工效率更快. 参考文献: [1] 沈琳燕, 李蓓智, 杨建国. 光学玻璃磨削机理的仿真研究[J]. 制造技术与机床, 2010(2): 104-107. [2] 李圣怡, 王卓, 吴宇列, 等. 基于研磨加工参数的亚表面损伤预测理论和试验研究[J]. 机械工程学报, 2009, 45(2): 192-198. [3] MILLER P E, SURATWALA T I, WONG L L,etal. The distribution of subsurface damage in fused silica[C]//Proceedings of SPIE: Laser-Induced Damage in Optical Materials. Bellingham: SPIE, 2005: 1-25. [4] 张银霞. 单晶硅片超精密磨削加工表面层损伤的研究[D]. 大连: 大连理工大学, 2006. [5] LAWN B R, EVANS A G, MARSHALL D B. Elastic/plastic indentation damage in ceramics: the median/radial crack system[J]. Journal of the American Ceramic Society, 1980, 63(9/10): 574-581. [6] MARSHALL D B, LAWN B R, EVANS A G. Elastic/plastic damage in ceramics: the lateral crack system[J]. Journal of the American Ceramic Society, 1982, 65(11): 561-566. [7] LI S Y, WANG Z, WU Y L. Relationship between subsurface damage and surface roughness of optical materials in grinding and lapping processes[J]. Journal of Materials Processing Technology, 2008, 205(1/2/3): 34-41. [8] 顾伟彬. 基于微纳米划擦特性的光学玻璃磨削机理与工艺研究[D]. 上海: 上海交通大学, 2012. [9] EVANS A G, CHARLES E A. Fracture toughness determination by indentation[J]. Journal of the American Ceramic Society, 2006, 59(7/8): 371-372. [10] CHEN S Y, FARRIS T N, CHANDRASEKAR S. Sliding micro indentation fracture of brittle materials[J]. Tribology Transactions, 1991, 34(2): 161-168. [11] JING X N, MAITI S, SUBHASH G. A new analytical model for estimation of scratch-induced damage in brittle solids[J]. Journal of the American Ceramic Society, 2007, 90(3): 885-892. [12] 韩帅. 大磨粒金刚石砂轮的精密修整及光学玻璃磨削试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. [13] 葛世荣, 朱华. 摩擦学的分形[M]. 北京: 机械工业出版社, 2005. [14] GHOSH N, SAHOO P. Finite element contact analysis of fractal surfaces[J]. Journal of Physics D (Applied Physics), 2007, 40(14): 390-393. [15] YAN W, KOMVOPOULOS K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics, 1998, 84(7): 3617-3624. [16] 曾祥有. 粗糙实体与理想平面弹塑性接触滑动摩擦模拟与分析[D]. 福州: 福州大学, 2010. [17] 孟彬彬. 光学玻璃磨削裂纹形成过程仿真及试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.2 结果分析
2.1 动态接触过程

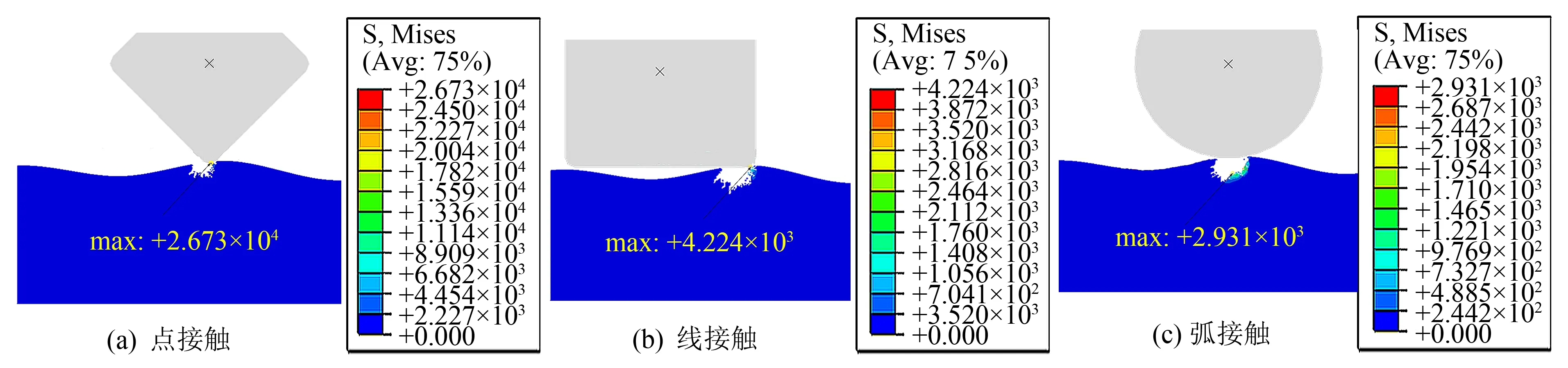
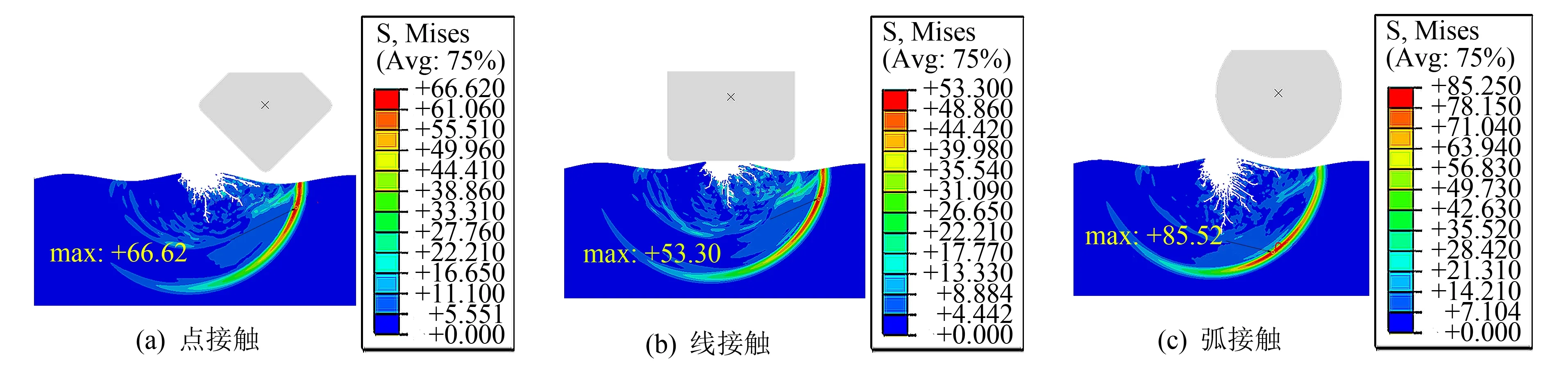

2.2 不同接触状态对亚表面损伤的影响
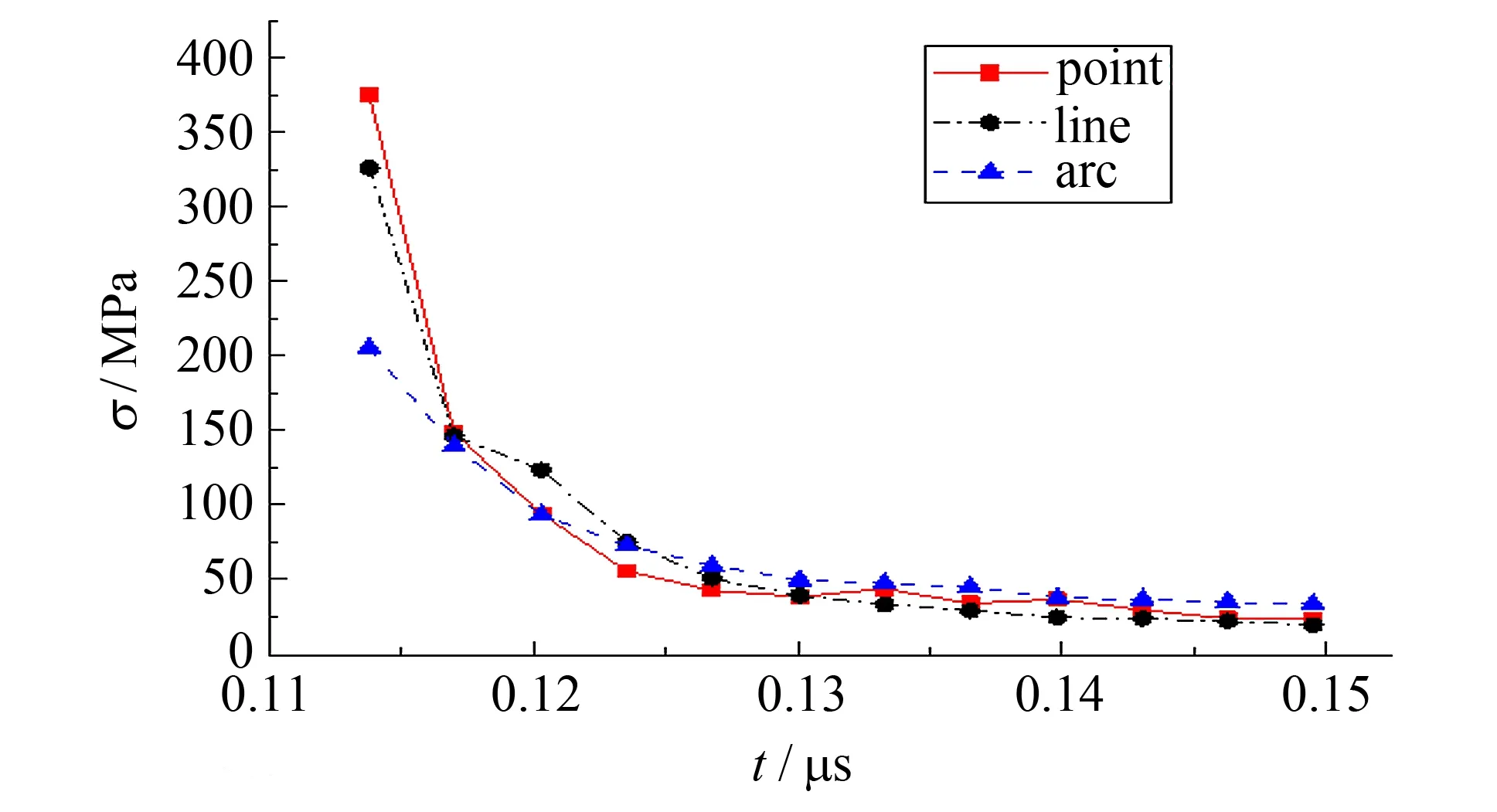
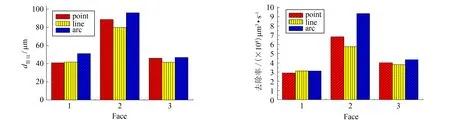
2.3 实验验证
3 结语

