声波多次往返叠加对相位比较法测量声速的影响

李 轩,方锦江，单桂晔,b，高志华,b

(东北师范大学a.物理学院;b.物理学国家级实验教学示范中心(东北师范大学),吉林 长春 130024)

声速测量是大学物理实验的基本题目，对学生深入理解振动叠加和驻波的相关理论知识以及声音传播的衰减现象有着重要作用． 驻波法和相位比较法是大学物理实验中测量声速的常用方法[1]. 驻波法是利用声波在发射器和接收器之间形成驻波，首先测量相邻波腹的间距得到波长，进而结合信号频率得到声速；相位比较法则将接收器的接收信号视为行波，利用声波相位随传播距离而滞后现象，通过比较接收器接收信号和发射器的发射信号的相位，测量出接收器接收信号的相位变化2π时移动的距离得到波长，进而得到声速． 目前，关于驻波法测量声速存在的问题已有较多研究，如：由于声波在传输过程中存在衰减使得接收器的接收信号振幅极大值随着收、发换能器间距增大而变小，且最小值不为零[2-4]；由于声波在收、发换能器间发生多次反射使得接收到的信号振幅极大值产生强弱交替分布的现象[5-6]；另外，研究还发现接收器接收到的信号为声压信号而不是振动信号[7]． 由于相位比较法利用两路信号同相或反相时李萨如图形合成一条直线段，通常被认为该方法测量声速更加准确[3-4]，目前对于相位比较法测量声速实验存在的问题研究较少． 实验中发现，得到的李萨如图形变化规律与理论预期并不一致，尤其当收、发换能器间距较小时，两信号合成的直线段在一个象限内会连续多次出现． 这对判断两信号的同相和反相状态造成严重影响，使得声速测量误差较大． 本文通过理论计算研究了声波的传输衰减、换能器表面反射系数以及声波在收、发换能器之间往复反射次数对声速测量的影响．

1 相位比较法测量声速原理

利用相位比较法测量声速装置如图1所示．将信号发生器的信号分别输入示波器X输入端和发射换能器，当信号频率达到超声换能器共振频率时，换能器辐射声波最强． 接收器接收超声波声压信号并将其转换为电信号输入示波器的Y通道，在示波器中可以观察到两信号合成的李萨如图形，由于两信号频率相同，因而李萨如图形为椭圆． 通过改变接收器的位置可改变接收器信号的相位，从而得到不同的李萨如图形． 理论上，当两信号的相位差为2kπ时(同相)，合振动轨迹在一、三象限形成一条直线，当两信号的相位差为(2k+1)π时(反相)，合振动轨迹为二、四象限的一条直线，其中k为整数，连续2次同相或反相对应接收器的移动距离为1个波长λ．

图1 相位比较法测量声速原理图

n=0,1,2,…

(1)

n=0,1,2,…

(2)

其中，A0为信号最初振幅，λ为声波波长，ω为角频率. 声场中各处的振动为

(3)

根据声学理论可得到各处的声压波动方程为[8]

(4)

其中ks为空气的绝热体变弹性模量． 李萨如图形的轨迹为

(5)

2 计算结果与分析

相位比较法测量声速,发射器和接收器信号合成的李萨如图形为椭圆． 当两信号的相位差为kπ(同相或反相),椭圆的短半轴为0；当两信号相位差为(2k+1)π/2时，椭圆的短半轴最大，式中k取整数． 随着两信号的相位差变化椭圆短半轴经历极大-极小-极大的周期性变化． 为了清楚地描述李萨如图形随接收器位置的变化的周期性，采用椭圆短半轴描述两信号的相位差变化的周期性, 图2为两信号振幅相同时椭圆短半轴与两信号相位差数值的对应关系，其中,图2(a)为合成椭圆的短半轴随接收器位置变化曲线，当短半轴为0时，对应两信号同相[图2(b)]或反相[图2(c)]; 当短半轴取值极大时，对应两信号相位差为π/2的奇数倍图2(d)． 图2中收、发换能器间距采用实际距离除以波长表示，即D/λ．

图2 椭圆短半轴与相位差对应关系

2.1 接收器接收的声压信号模拟分析

超声声速仪的发射器和接收器由压电陶瓷制作而成. 发射器利用压电材料的逆压电效应，压电陶瓷环片在交变电压作用下，发生纵向机械振动，在空气中激发超声波，把电信号转变成声信号. 接收器利用的是压电材料的压电效应，空气振动使压电陶瓷环片发生机械形变，从而产生电场，把声信号转变成电信号. 由于学生对超声换能器比较陌生，对声换能器的接收信号也缺乏了解，很多学生误认为超声声速仪的接收器接收到的空气分子的振动信号． 当不考虑换能器转换信号所造成的延迟，根据式(4)可知，声压信号比振动信号的相位滞后π/2, 为了直观地表明这种差异，模拟了无传输衰减的声波振动信号、有传输衰减振动信号和有传输衰减声压信号分别相对于发射信号的相位差随收、发换能器间距增加的变化规律，衰减系数取为α=0.02 dB/mm[6]，信号频率设为40 kHz，结果如图3所示． 可见，传输衰减不能改变信号的振动周期，虽然接收器处的声压信号和空气分子振动信号存在相位差，但两信号的周期性完全相同，因而利用声压信号测量声速是合理的．

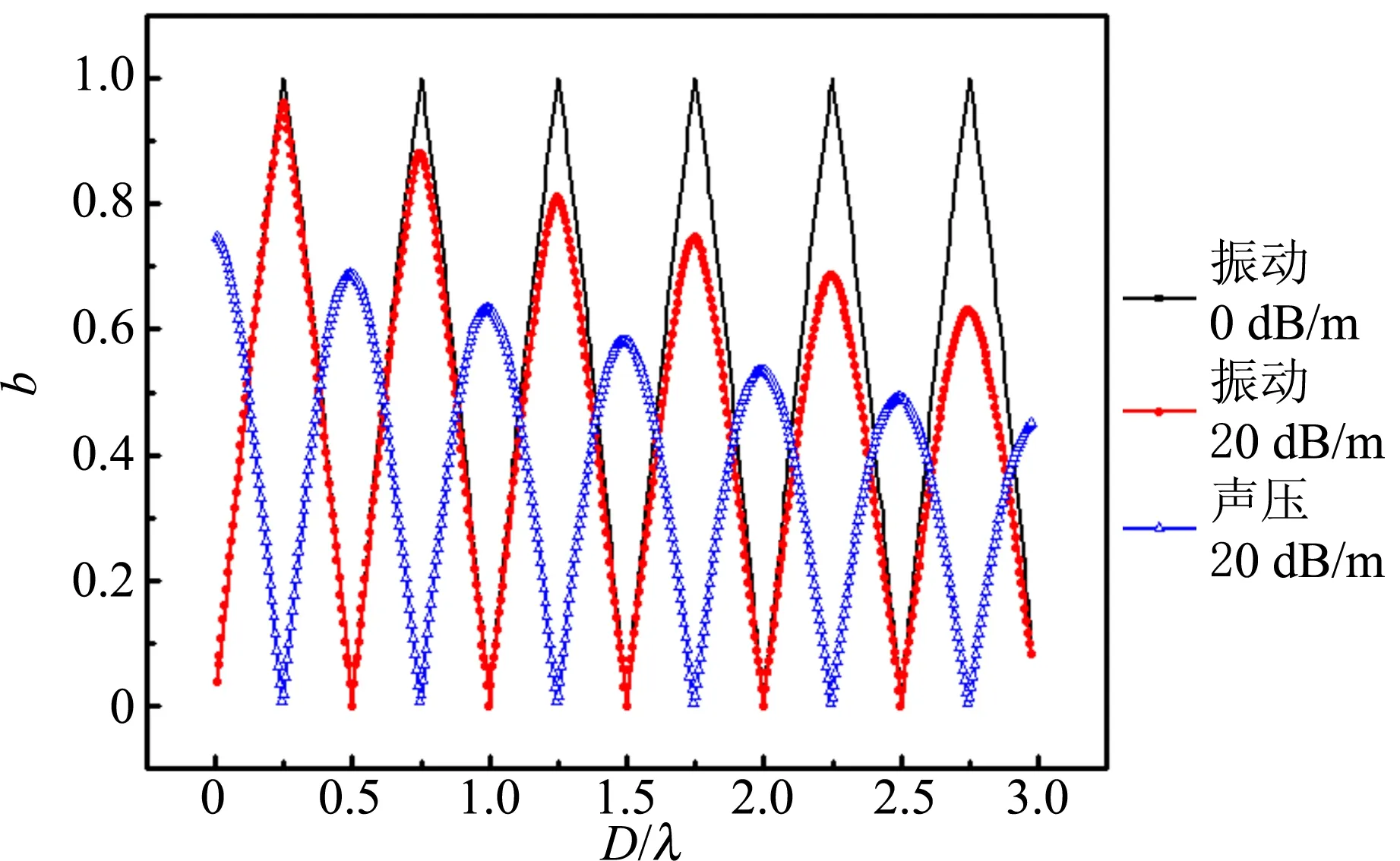
图3 声压信号与质点振动信号对李萨如图形影响

2.2 信号往复传播叠加次数对李萨如图形的影响

利用相位比较法测量声波波长时，示波器X输入信号为发射器的输入信号x(0,t)，Y输入为接收器的声压信号，由于声波的传输衰减，接收器的声压信号p(x,t)的振幅随着接收器与发射器的距离增大而逐渐减小. 若保持示波器信号各通道的衰减不变，则两信号同相和反相时观察到直线段随着收、发换能器间距增大，长度将逐渐减小，与水平轴夹角逐渐减小，这些不会引起测量误差． 然而，实验发现，接收器和发射器间距在λ内出现的同相和反相的次数之和多于2，如图4所示，其中图4(a)～(e)为同相，图4(f)～(i)为反相． 在接收器移动1个波长李萨如图形接近直线的情况出现9次，这与理论分析矛盾，分析造成这一现象的原因，可使学生避免实验测量出现错误，加深学生对波的叠加规律的理解.

(a) (b)

(c) (d)

(e) (f)

(g) (h)

(i) (j)图4 相位比较法测量声速实验现象

根据式(3)～(4)可知，当n取不同值时，声压信号是由振幅不同的正弦和余弦函数相加得到，其合成的李萨如图形随接收器位置移动变化复杂. 不同往复叠加次数n的取值对合成李萨如图形的影响如图5所示. 图5中列出n=0,n=1和n=7时椭圆短半轴随收、发换能器间距增加的变化情况． 传输衰减系数取为20 dB/m，反射系数取0.8.

图5 反射次数对李萨如图形的影响

比较图5中3条曲线可知，当接收器位置一定，随着n增加，合成椭圆的短半轴极大值逐渐增大，这是由于信号往返次数越多，到达接收器的能量越大，而往返次数越少，到达接收器的信号能量越少． 另外，当计入的往返次数足够多时(N=7)，在收、发换能器间距较小时(小于λ/2)，椭圆短半轴的数值在极小值附近出现多次反复，与图4所示现象相一致. 随着收、发换能器间距增大，这种现象逐渐减弱消失． 可见，由于声波信号在收、发换能器间多次往返，使得合成的李萨如图形变化复杂，反射次数越多对实验影响越大． 因此，利用相位比较法测量声速时，可采取措施减少声波在收、发换能器间反射次数，测量时避开收、发换能器间距较小的位置．

2.3 换能器表面反射系数对李萨如图形的影响

由于超声换能器的制作材料、使用状况不同，表面的清洁和光滑程度存在差异，因而对声波的反射系数不同． 反射系数决定了信号多次往复叠加的能量大小，因而影响李萨如图形形状． 图6列出了换能器反射系数分别为0.6，0.8和1.0时，椭圆短半轴随收、发换能器间距的变化，图中α=20 dB/m,n=7．

由图6中可知，随换能器表面反射系数增大，接收器接收信号能量增强，椭圆短半轴极大值逐渐增大，这有利于实验观测；对于不同换能器表面反射系数，椭圆短半轴极大值出现的位置相同；当收、发换能器间距较小(小于λ)时，换能器表面反射系数越大，接收器信号与发射信号同相或反相状态连续出现的现象越明显，且维持的空间范围也越大，随收、发换能器间距增大该现象逐渐消失． 可见，换能器表面反射系数大使得李萨如图形变得复杂，不利于实验测量，为避免同相和反相状态连续出现的现象，可采取措施适当减小换能器表面的反射系数，使其既能有效反射声波又能避免此现象的影响，另外，避开收、发换能器间距较小的区域进行测量也是有效方法．

图6 反射系数对李萨如图形的影响

2.4 声波传输衰减对李萨如图形的影响

声波在介质中的传输衰减包括介质的吸收衰减和由于声波发射产生的几何衰减，实验中由于收、发换能器间距较小，且两换能器采用正对的方式，因此，可忽略声波的几何衰减． 空气吸收衰减系数越大，接收器接收的叠加声波信号幅值越小，在相同的收、发换能器间距上，反射次数越多幅值越小，合成的直线段长度极大值和倾角随着收、发换能器间距改变而改变． 图7列出了当α分别取1,10,20 dB/m时合成椭圆短半轴随收、发换能器间距的变化情况． 为方便比较，将10 dB/m 和20 dB/m曲线做了向上平移．此处β=0.8，n=7．

图7 反射系数对李萨如图形的影响

由图7可以看出，当声波传输衰减系数较小(1 dB/m)时，两信号同相或近同相和反相或近反相连续出现的现象更明显，且保持的空间范围更大，这对会造成学生对实验现象的误判. 当接收器位置一定时，声波传输衰减系数越大，合成椭圆短半轴极大值越小，李萨如图形越小，因此不利于实验信号观测，通过调节示波器的信号衰减倍数，可使图形变大利于观测． 随着收、发换能器间距增加，上述现象逐渐消失，但是由于声波信号衰减，李萨如图形会变小，也不利于实验观测． 可见，声波传输衰减有利于降低连续出现的同相和反相现象，但也会造成李萨如图形变小不利于观测． 为了获得适合实验观测的李萨如图形，一方面应适当选择对超声吸收不太强的介质，另一方面，避开收、发换能器间距较小的区域进行观测．

3 结 论

通过计算发射器、接收器信号合成的椭圆短半轴，研究了造成相位比较法测量声速实验中，连续多次出现同相或近同相和反相或近反相现象． 研究表明:收、发换能器之间的往返叠加次数越多、声波在换能器表面的反射系数越大和传输衰减越小，在收、发换能器间距约小，该现象越明显，反之越弱． 研究还表明:各因素不影响合成信号的同相和反相出现的周期性． 另外，理论计算证明了利用超声换能器接收声压信号进行相位比较法测量声速的合理性．

参考文献：

[1] 杨述武，孙迎春，沈国土. 普通物理实验(一、力学、热学部分)[M]. 5版. 北京:高等教育出版社出版, 2015:107-112.

[2] 邓小玖,宋勇,高峰,等. 声速测量实验的研究及数值模拟[J]. 物理与工程, 2006,16(2):24-25.

[3] 张涛,吴胜举,张永元. 空气中声速测量实验研究[J]. 陕西师范大学学报(自然科学版),2004,32(1):44-46.

[4] 谢莉莎,刘彩霞,肖苏,等. 能量损耗对超声声速测量影响的进一步研究[J]. 大学物理实验, 2005,18(3):1-3.

[5] 孙航宾,黄笃之,张禹涛. 声速测量实验假象的探讨[J]. 大学物理实验,2011,24(4):50-52.

[6] 李乐天,关健慧,夏柱红,等. 驻波法测声速实验中峰值强弱交替现象的研究[J]. 物理与工程, 2016(s1):84-87.

[7] 陈殿伟,盖啸尘,王严东. 驻波法测定超声波声速实验的探究[J]. 大学物理实验,2006,19(3):36-39.

[8] 张三慧. 大学物理学(波动与光学)[M]． 北京：清华大学出版社，2000：83-84．