橡胶气球大小与内外压强差关系

吴 昕，王雪彬

(南京市金陵中学，江苏 南京 210005)

从物理角度来看：肥皂泡在阳光的照射下，肥皂泡的里外表面反射的光发生干涉引起颜色变化[1]，而色泽的变幻莫测与重力下的液体的分布改变以及表面液体挥发状态有关． 吹肥皂泡要用力，在肥皂泡的形成过程中做功，根据功能转化原理，肥皂泡的形成过程有能量的积累[2],肥皂泡积累的能量是表面能，肥皂泡的膜面上存在着支撑肥皂泡的表面张力． 肥皂泡因为很难控制和测量，因此用气球来作为研究对象． 为了更好地了解实际的气球内外的压力差和半径之间关系，本文进行了相关的实验和理论定量分析．

1 橡胶气球连通实验

因为表面张力的作用，液体球面凹面一侧的压强应大于凸面一侧的压强．在此情况下，液面两侧的压强差Δp与表面张力系数α成正比，与曲率半径R成反比，即

Δp=2α/R.

(1)

(1)式是球面膜的拉普拉斯定律[2]． 对于肥皂泡来说，有内外2个液体-空气界面，都满足凹面一侧的压强总是大于凸面一侧的压强，因此，肥皂泡内外的压强差是单个膜面压强差的2倍，即

Δp=p2-p0=4α/R.

(2)

比较好的演示实验是一大一小2个气球，用连通器连在一起，一般想应该是2个球变成一样大，但实际并非如此． 图1中2个气球，红色大一些的气球直径约为16.6 cm，蓝色小一些的气球直径约为13.8 cm，把它们用硬管和软管连起来，打开中间的夹子，可以发现，红色的气球变大最终直径约为19.3 cm，蓝色的气球变小最终直径约为5.6 cm．

(a)连通前

(b)连通后图1 气球连通器的实验

该实验大致验证了球面膜的拉普拉斯定律，但是，蓝色球也并未完全缩到自然尺寸2.4 cm(该气球正常状态下平铺时中间的长度约为7.5 cm，因此计算出常压下周长约为15 cm，计算出气球此时直径约为2.4 cm)． 而且，并不是所有的实验都出现大球变大小球变小的情况，在球的直径较大的情况下，有时没有发现明显的球半径的变化，甚至有时出现大球变小、小球变大的情况．

2 橡胶气球实际内外压力差的测量

为了量化得到气球内外的压强差Δp和直径d之间的关系，设计的定量测量实验装置如图2所示．将吹好的气球连在软管做成的连通器一端，软管内注入一定量的滴有墨水的水，方便测量左右软管中的水柱高度差Δh，得到气球和外界大气的压强差Δp． 1 cm的水柱大约相当于100 Pa．

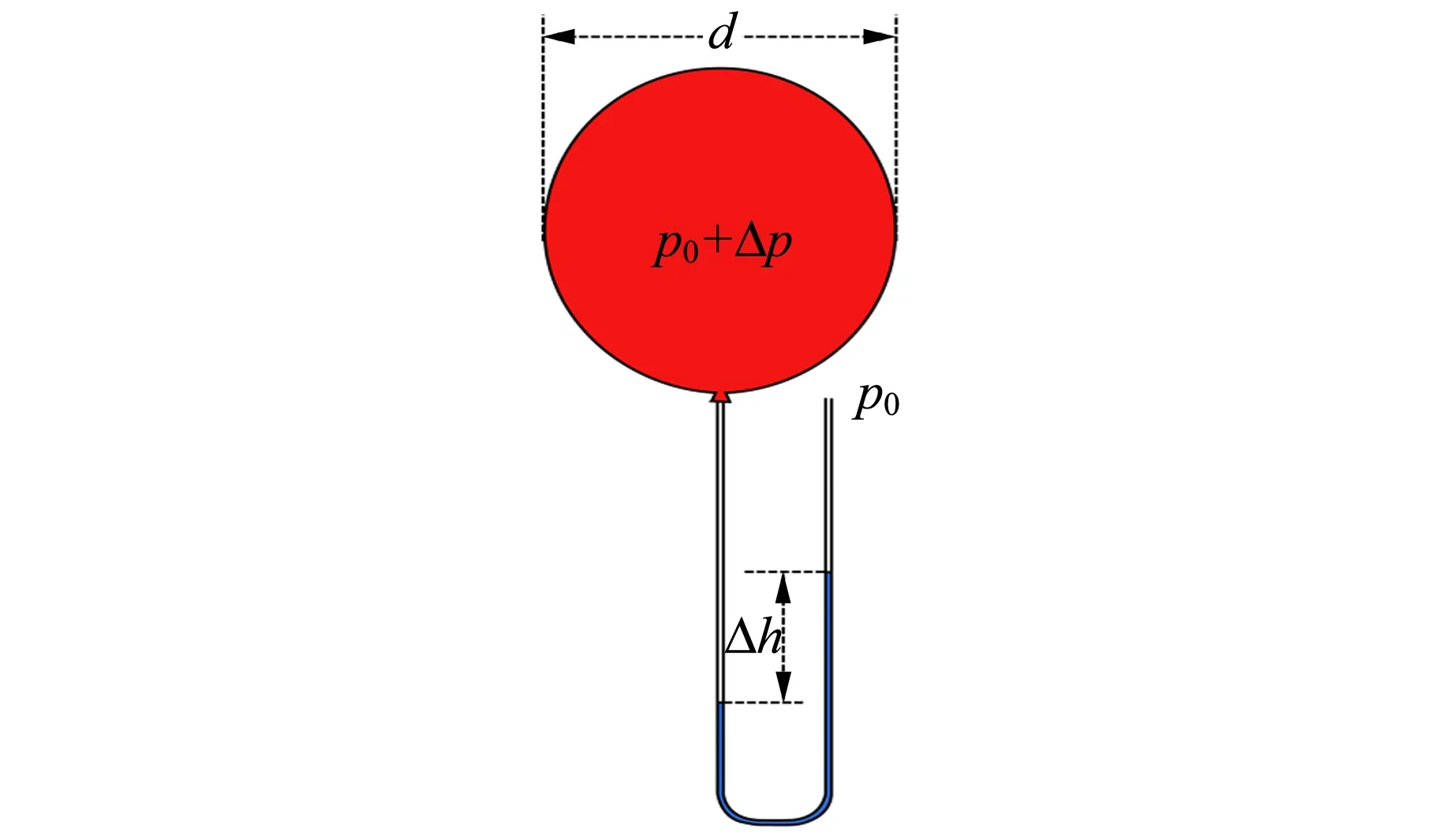
图2 实验装置示意图

通过与气球连接的三通的一端放气，使得气球直径逐渐减小，在这个过程中同时测量气球的直径和连通器两侧的水柱高度差，得到连通器左右液面高度差随气球直径的变化关系，测量数据如图3所示．

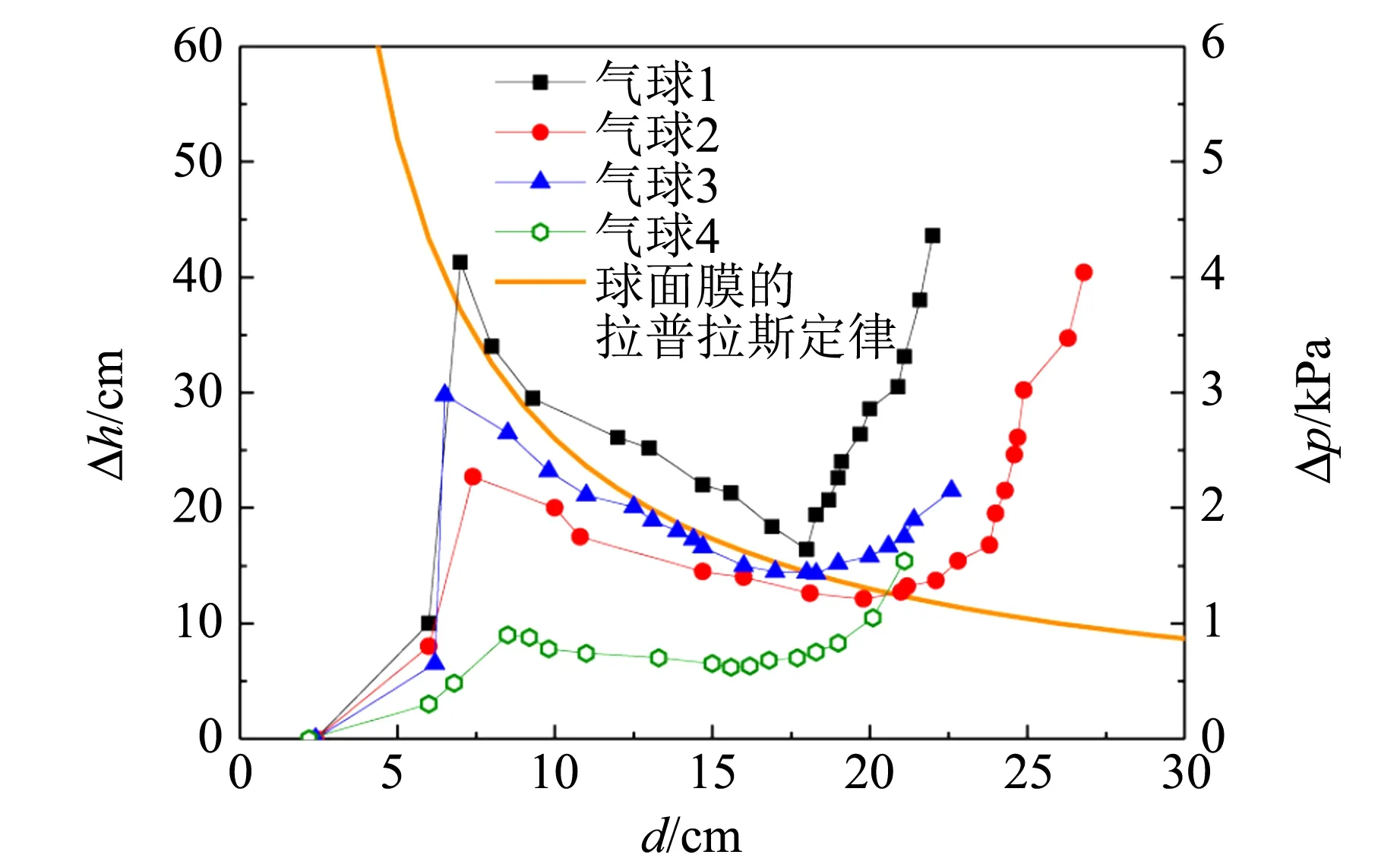
图3 不同气球测量得到的压强差Δp与直径d关系

气球1～3的材质相同，为质量稍好的气球，它们的结果比较一致；而气球4则质量较差． 通过图3可以看到气球内外气压差Δp从气球开始处于未拉升的正常状态，随着半径变大即充气内外强力差急剧增大(此范围在实验中非常难测量，因为很小的直径变化会造成很大的压强差升高)． 当直径增加到一定范围后压强差又会逐渐减小，在这一中间范围(对于气球1～3大致为7～17 cm)大致满足球面膜的拉普拉斯定律，而质量较差的气球4在该区域内随着直径增加压强减小得不明显． 图1气球连通器实验中所用的质量较好的红色气球直径约为16.6 cm，蓝气球直径约为13.8 cm，刚好大致满足球面膜的拉普拉斯定律的直径范围内，因此出现了大球变大、小球变小的现象． 但是如果球直径继续增加，不再满足球面膜的拉普拉斯定律，即随着气球的增加，内外压强差会增加，因此对于气球连通器实验，当大球吹得更大到达20 cm以上，不一定出现大球变大小球变小的现象，最终的状态会更加复杂．

3 实验结果讨论与模拟

上述实验，相对简单，有些问题没有考虑，比如：气球其实是个椭球，但在测量气球的直径过程中，只测量了气球横向的直径，作为标准的球；气球在吹气口那段无法从理论模型放到结果中去，但通常这一部分的橡胶会随着气球的增大，少量地进入到气球的总体薄膜里面去；气球的材质是橡胶，拉和缩的性质不一定可逆，在这个过程中可能吹气到某个直径或者放气到某个直径对应的内外压强差不同，当然因为橡胶疲劳等原因，第二次测量和第一次也可能不同． 但上述问题不妨碍本实验作为定性而非准确定量的实验研究气球的吹气问题[3-4]．

假设橡胶气球是各向同性的球形薄膜，即不考虑气球的不规则性或者气球扎口部分的影响． 考虑到形变的气球的某个过球心的圆切面，球面橡胶形变的弹力提供橡胶薄膜的“表面张力”． 假设均匀橡胶气球的单位长度的弹力密度为T，该弹力和液面膜的表面张力系数α量纲相同，在某个(如图4所示)截面，膜面1周对应的弹力密度在该平面的分量为Tsinθ，根据截面的压力与弹力平衡关系，可以得到：

Tsinθ·2πRsinθ=ΔR·π(Rsinθ)2，

(2)

即

2T=Δp·R.

(3)

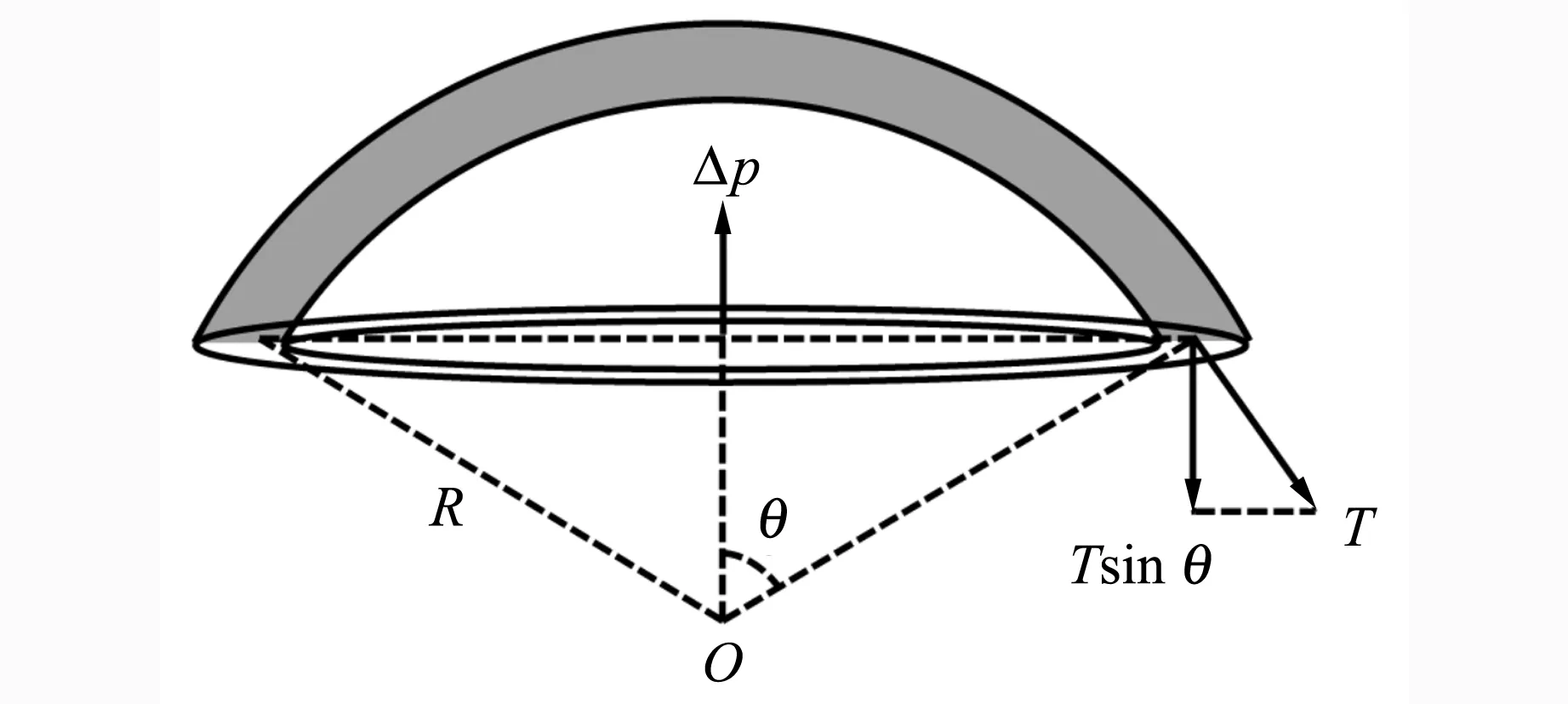
图4 标准球形气球内外压强差的计算

(3)式的推导和球面膜的拉普拉斯定律推导过程[2]基本相同，结果在形式上也完全相同． 但是实际上，橡胶气球薄膜是弹性较大的固体材料，和液体球的表面有很大的区别． 液体的表面张力不牵涉到内部液体的贡献，仅由液体和空气接触的介面个数有关，因此作为单位长度的表面张力——表面张力系数和构成表面的液体厚度理论上没有关系． 而对于固体弹性薄膜来说，应力σ——分布在单位截面上的弹性力——才是材料受力更基本的量度，而应力和单位长度弹力密度T之间刚好相差厚度δ，即T=σδ． 在气球直径变大的过程中，因为气球膨胀橡胶膜厚度变小，与液体表面张力系数对应的T在橡胶气球中同时受到应力和厚度的影响，变化关系会非常复杂. 因此实际测量的橡胶气球内外压强差和球面(液)膜的拉普拉斯定律不一致是可以理解的．

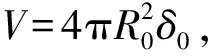
σ=E(λ-1).

(4)

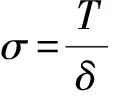
(5)

(a)

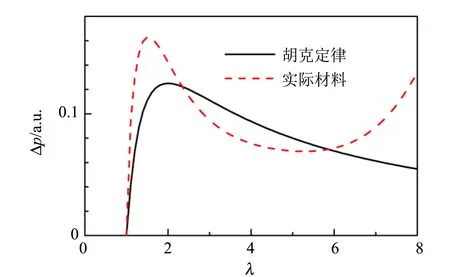
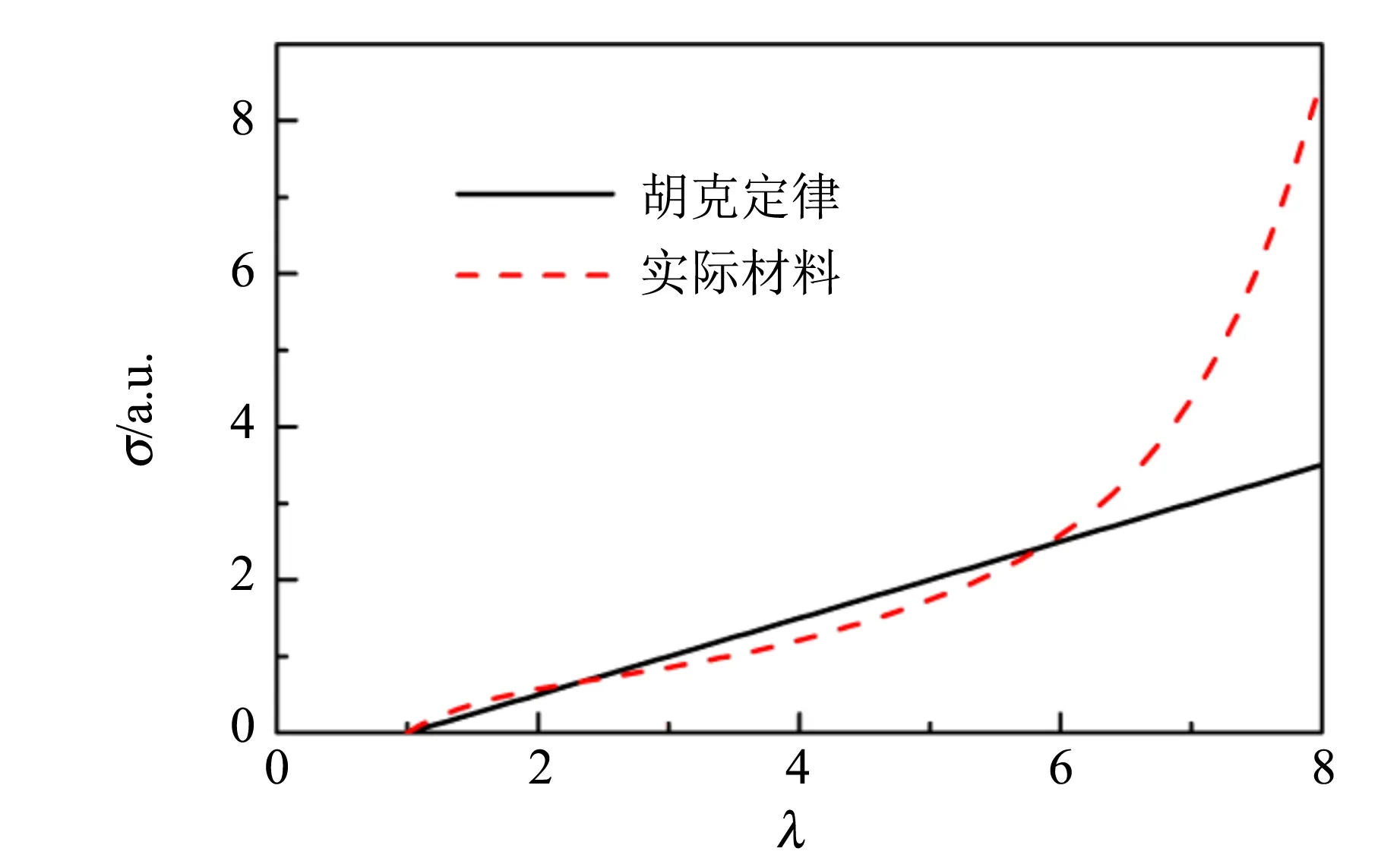
(b)图5 应力和气球压力差随约化半径的关系

因此可以断定，气球的橡胶一定不满足胡克定律，即橡胶不是普通的固体材料，应变可以达到自身体积的百倍，杨氏模量数值也非常小即它很容易发生形变． 考虑到橡胶是高分子材料，那么熵弹性可以作为形变应力的主要来源． 在只考虑熵的贡献和弹性，不考虑黏性和构象能，并在其体积保持不变的情况下，可以基于网链交联的理论[6]得到其应力和约化形变的关系

(6)

当形变量较大时，1/λ2基本可以忽略，因此和(4)式的结果类似． 而实际测量的橡胶材料得到的应力和约化形变的关系非常复杂，如图5(a)的红色虚线所示，偏离理论关系的原因可能是大的形变下有无效的松链以及应力诱导结晶的存在[6]，使得材料偏离理想网络的模型． 基于橡胶材料的应力和约化形变的关系，可以得到图5(b)红色虚线所示的压强差和约化半径的关系，发现该曲线和实验的结果非常吻合，因此随着半径增大，气球内外压强差后面又升高的情况是由大形变下气球橡胶材料的性质所决定． 而质量较差的气球4，小半径范围内半径增加压强差减小的情况不明显，应该和橡胶质量较差有关．

4 结束语

球面液膜的拉普拉斯定律指出，在理想情况下液体气泡内外压强差应该和它的半径成反比． 但是对于橡胶气球，实验表明气球内外压强差随着半径的变化非常复杂，先随着半径增加迅速增加，再慢慢降低，再到逐渐增加． 在气球中，表面张力是由气球橡胶模的形变产生，所以和液体膜有很大差别，通过对材料形变和弹力的关系的理解，定量理解了气球的内外压强差随直径变化这一复杂的关系．

致谢：感谢金陵中学“准博士培养站”项目的支持和南京大学杨欢教授提供的帮助！

参考文献：

[1] 程守洙，江之永． 普通物理(下册)[M]． 6版. 北京：高等教育出版社，2006：141-148．

[2] 王光昶． 医学物理学[M]． 北京：清华大学出版社，2011：110-114．

[3] 黄思议，班尔达，陈思聪，等． 气球的非线性力学特性探究[J]． 高中数理化，2012 (20)：46-47．

[4] 陈理． 大小气球对接现象的量化解释[J]． 中学物理教学参考，2013，42(12)：50-52．

[5] 李宾中． 医学物理学[M]． 北京：科学出版社，2010：29-36.

[6] 华幼卿，金日光． 高分子物理[M]． 4版. 北京：化学工业出版社，2013：168-187．

[7] 高志华，闫妍，申燕． 水流冲不走乒乓球现象的研究[J]． 物理实验，2017，37(6)：14-18.