动态积云绘制算法的实现与分析

柏靖云

（四川大学计算机学院，成都 610065）

0 引言

随着计算机技术的快速发展和图形硬件的更新换代，计算机图形学正以令人惊叹的速度发展着，作为图形学中的一个重要组成部分，自然景观的模拟也广泛应用到了各个领域，而这其中，对于云的绘制也受到了越来越多的关注。现今在影视特效、多媒体广告、游戏场景等多个领域都需要对云进行模拟。绘制出真实自然的云场景，可以很大程度上提高画面质量，带给人强烈的真实感。然而云有着极不规则的形状和不规律的变化，云内部的光照过程也十分复杂，要完整地将这些表现出来非常困难，而且需要很大的开销。如何用较高的效率绘制出具有较强真实感的积云场景，一直是相关研究学者们非常关注的问题之一。

1 云的绘制算法简介

云的绘制可大致分为建模和渲染两个部分，建模部分需要构造出云的形状密度模型，渲染部分则根据云的密度，采用特定的光照算法计算出云的颜色，并最终将云在屏幕上显示出来。本文采用两种方法分别对云进行绘制，方法一将云视为是由多个球形云粒子堆积而成的，通过绘制粒子来对云进行建模，同时采用预计算的方式，将云粒子的多重散射光照结果存入查找表中（look-up table），在实时渲染时直接到相应的纹理中采样，即可获得光照数据，省去了光照计算过程。方法二通过噪声纹理来获取云的密度，再对噪声值进行一系列的分布、高度处理后，最终得到云的密度场，即云的模型。使用以比尔定律为基础的光照方程计算云的颜色，最后采用ray marching的方式对云进行绘制。

2 多重散射光照模型

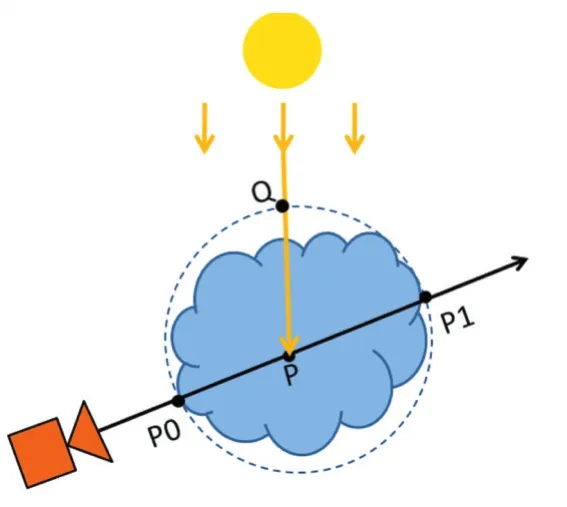
图1

当光在云中传播时，云粒子会对光产生散射作用。如图1所示，对于云粒子中任意一点P，在视点C所看到的P点的最终光照是经过了QP与P0P两段衰减的。假设最初的太阳光光照总量为L，经过一次散射后的光照为L'，L与L'的关系如公式（1）所示:

e-τ(Q,P)和e-τ(P0,P)分别为 QP 之间与 P0P 之间的散射衰减系数。公式（1）描述了太阳光在云粒子中发生单散射的过程，而实际上，光在粒子内部会经历很多次散射，到达P点的光也不只有初始太阳光L，还有粒子中其他点散射到P点的光，因此，为了更加真实地模拟云的光照效果，需要构建多重散射的光照模型。

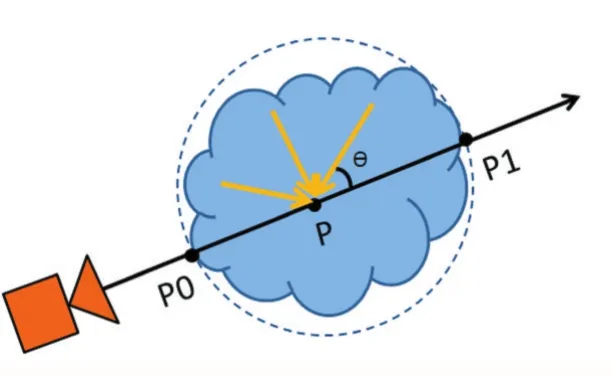
图2

在多重散射中，P点的光照由P点周围各个方向上经过散射后最终到达P点的光组成。如图2所示，P点在方向的入射光为，将θ从 0 取到 2π时的所有L(P)相加，即为 P点的入射光总量，如公式（2）所示。将入射光乘以P0P之间的散射系数，再对P0P1间所有点的光照结果进行积分，就可以得到视点位置为C、视线方向为时的光照颜色，如公式（3）所示。

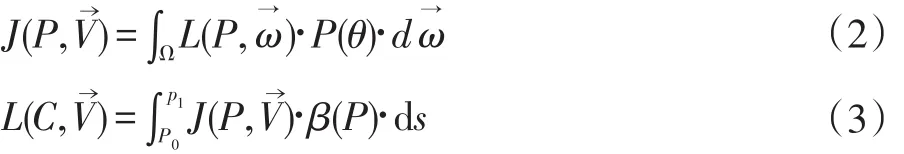
在计算过程中，本文采用对单散射结果进行迭代的方法来得到多重散射数据。先使用单散射方式得到一阶散射结果L(1)(P,)，然后根据L(1)(P,)可计算出J(2)(P)，再依据公式（3）可得到L(2)(C,)，而此时得到的二阶散射结果可用于计算下一次的散射L(2)(P,)，依此类推，在经过n次迭代之后，就可以得到n阶散射结果L(n)(C,)，再将n阶结果相加，即为最终的多重散射光照，如公式（4）、（5）、（6）所示：

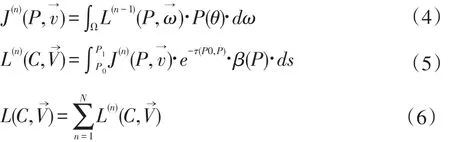
在本文所采用的算法中，多重散射结果为18阶散射数据之和，如果让18次迭代过程全部在渲染中进行，则会严重影响程序的效率，完全无法达到实时的效果。因此本文使用预计算的方法来避免这一问题，在渲染云粒子之前先计算光照，然后将计算结果存入查找表中，查找表为一张三维纹理，渲染时，根据粒子的位置和视线方向等参数可直接从查找表中读取光照数据。

3 球形粒子建模

本文实现的第一种方法是通过构造成千上万的云粒子，根据相应的算法使其堆积成云团的形状，再将粒子绘制出来。如图3所示，以视点为中心，构造xz平面的二维网格，每一层网格的大小都是上一层网格的二倍。将密度纹理平铺在网格上，达到一定密度值的网格视为有效网格，通过视锥体确定哪些网格在视线范围内，得到二维的有效可视网格。

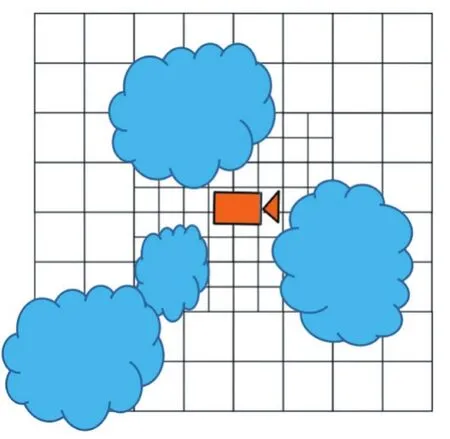
图3

得到二维网格后，将其纵向延伸成三维网格，三维网格中每个体素的密度由其原本对应的平面网格进行一定的噪声扰动得到，同时令体素密度随着层数的上升而递减，以此可获得下宽上窄的积云形状。在三维网格结构中，每一个有效可视的体素均含有一个云粒子，粒子的大小、密度、中心位置等属性由网格的相应属性计算得到。生成粒子后，将粒子根据与视点的距离排序，按照由远及近的顺序进行渲染。

此种方法在渲染时使用到了渲染管线中的几何着色器，由顶点着色器将粒子位置传送给几何着色器，几何着色器以此为中心，根据粒子大小（即半径）生成一个正方体粒子包围盒。几何着色器发射八个顶点传送给片元着色器，片元着色器判断视线与包围盒的交点，如相交，则到光照查找表中获取多重散射系数，将粒子绘制到屏幕上。

4 基于噪声纹理采样的绘制方法

本文实现的第二种方法是以柏林（Perlin）噪声和沃利（Worley）噪声为基础的。构建云的密度场需要两张三维纹理，这两张三维纹理中共包含了八张噪声纹理信息。纹理一的分辨率为128×128×128，如图4所示，其r通道为柏林噪声，gba三个通道为三张频率依次升高的沃利噪声。纹理二的分辨率为32×32×32，如图5所示，RGBA四个通道分别为四张频率依次升高的沃利噪声。纹理一用于得到云的基本形状，纹理二用于给纹理一得到的结果添加细节。得到云密度后，再通过分布纹理对其进行细化，添加高度控制函数和动态变化函数，使云层分布随着海拔升高而减少，同时产生随着一定风向飘动的动态效果。

图4

图5

此方法的光照计算以beer定律为基础，如公式（7）所示，比尔定律描述了光在不均匀介质中传播时的衰减过程，光照随着云的密度的增加成指数递减。

通过比尔定律可以计算出光的衰减，但光在云中传播时不止发生衰减，还会在云的内部产生复杂的散射，如果只计算衰减部分，那么我们将无法得到云表面的不规则的波浪状的细节，因此除比尔定律外，还需要添加内散射函数来描述光的散射过程，如公式（8）所示:

当光在诸如积云这类由细小微粒组成的介质中传播时，被散射到贴近光线传播方向部分的光线要多于被散射到背离光线传播方向的光线，如图6所示，这是光在云中所发生的前向散射。1941年，Heyey和Greenstein提出了H-G相位函数来对这一特性进行描述，如公式（9）所示，本文采用了这一方法，g的取值为0.2，θ为光纤与视线的夹角。

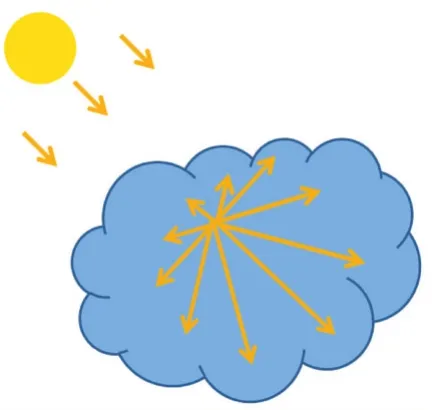
图6

本文采用ray marching的方法进行绘制。求出每一条视线与云层的交点，设定相应的步长，在两个交点之间选取采样点，得到每个采样点的世界坐标，从噪声纹理和分布纹理中查找出相应数据，经过上述一系列操作，得到该点的密度值，再将密度值代入到光照模型中，即可计算得出该点的光照颜色，最后将视线上每个采样点的颜色进行混合，就是该片元的最终渲染结果。

5 实验结果对比

图7

如图7所示，图a为三维网格球形粒子建模方法的结果，图b为基于噪声纹理采样方法的结果。球形粒子建模方法的结果可看出云的层次结构更为明显，云由多层粒子堆积而成，且距顶端越近粒子越少，云也就越窄。噪声纹理采样的结果层次感不如球形粒子建模，但是更好地模拟出了云的细碎且不规则的边界，在这一点上更具有真实感。

图8为当视点处于云层之上时，俯视角度下的结果。这里可以看出球形粒子建模方法的劣势，俯视时效果接近于平面，这与现实中的云的效果是差别很大的，而噪声采样的结果要更加贴近真实，俯视时此种方法在云的表面细节上所具有的优势更加明显。

图8

图9

图9为视点处于云中时，即穿云时的结果。球形粒子建模可以清晰看出分布在视点两层的云，而噪声纹理采样的结果则更能给人以深处云层之中的感觉。

通过以上对比可看出，当视点位于云层下方时，球形粒子建模方法得到的效果更好，这种情况下一般视点距离云较远，因此对边界细节的要求不高，云整体的分布和层次感更为重要。而当视点处于云层中间或云层之上时，则时噪声纹理采样的结果更加具有真实感，此时视点离云比较近，因此需要模拟出云的边界细节。在实际应用中，应根据应用的情况选择更为适合的方法。

6 结语

本文实现了两种动态积云绘制算法，并对其效果进行了比较。球形粒子建模结合预计算光照渲染的算法得到的积云更具与层次感，整体形状更接近现实中的云；噪声纹理采样结合beer定律光照模型得到的积云拥有更加丰富真实外观细节，适用于当视点离云层很近的穿云或俯视效果。

本文所实现的两种方法在最终渲染时的混合上都还有可提升的空间，粒子建模方法中最中前后粒子的混合与噪声采样方法中各采样点颜色的混合，目前都是采用比较基础简单的混合方法，还可以对混合方式进行改进以便获得更为逼真的效果。

参考文献：

[1]Ament M，Sadlo F,Weiskopf D.Ambient Volume Scattering[J].IEEE Trans.Vis.Compute.Graph，2013.

[2]Bruneton E,Neyret M．Precomputd Atmospheric Scattering[J].Compute.Graph,2008.

[3]K Perlin.An Image Synthesizer[C].New York：Proceedings of the 12th Annual Conference on Computer Graphics and Interactive Techniques，1985.

[4]LosaSSO F,Hoppe H．Terrain Rendering Using Nested Regular Grids[J]．ACM trans.Graph,2004.