基于粒子群算法的观测平台轨迹优化方法研究

赵琛，李健，师海云

（四川大学电子信息学院，成都 610065）

0 引言

随着反辐射导弹技术以及电子对抗技术的发展，一些有源探测方法，如雷达等，正在受到威胁。无源定位系统由于其隐蔽性，得到了很好的发展，根据无源定位体制又可以分为时差无源定位系统、测向定位系统、到达频差定位系统等[1,2]，其中，时差无源定位（TDOA）技术由于其定位精度相对较高、工作频带宽、对辐射源频率未知、快变的情况具有良好的适应性等优势，受到了研究人员的关注。

在时差无源定位系统中，定位的精度和辐射源与观测平台的相对几何位置有关。目前，大部分研究成果也集中在此方面。其中，文献[3-6]研究了几种常见的布站方式的定位精度的差异，并用实验验证了基线长度与基线角对精度的影响。文献[7]用自适应遗传算法找到静止目标的最优布站。但上述研究的前提均是目标静止，而实际情况中，目标运动的情况居多，此时，用目标静止的方法来进行处理会导致观测器测量误差累计增大，最终将对目标失去跟踪与定位。

针对以上不足，本文提出了一种基于粒子群算法的多观测平台轨迹优化方法，将轨迹优化问题转换为带各观测平台下一时刻的运动方向以及速度调整因子的GDOP的非线性优化问题，并用粒子群算法对该问题进行实时求解，并就最优布站情况对目标进行时差无源定位，将得出的目标位置作为滤波输入，得到下一时刻目标的预测值，从而进行下一轮的迭代。

1 目标函数的确定

在时差无源定位系统中衡量定位精度的一个重要指标是误差几何稀释度（GDOP）值，它用来描述定位误差的几何分布[8]。下面以三站时差定位体系为例，对其GDOP进行推导。

在三站时差定位体系由一个主站——(x0,y0,z0)T和两个副站——(x1,y1,z1)T、(x2,y2,z2)T构成，辐射源的位置为(xt,yt,zt)T，r0为辐射源与主站的距离，r1和r2分别表示辐射源与两个副站之间的距离，Δr1和Δr2分别表示两个副站到辐射源之间的距离与到主站之间的距离的差值。

在三观测平台下，理论上只能对观测平台所在平面内的辐射源进行定位，但这必然会给定位带来一定的误差，为了降低这个系统误差，可以根据已知条件对辐射源的高度进行合理假设，这里我们将其设为，则定位方程为：

将上式中的最后一个等式两边进行微分：

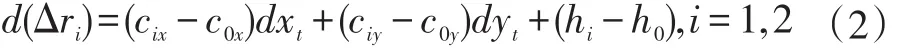
其中：

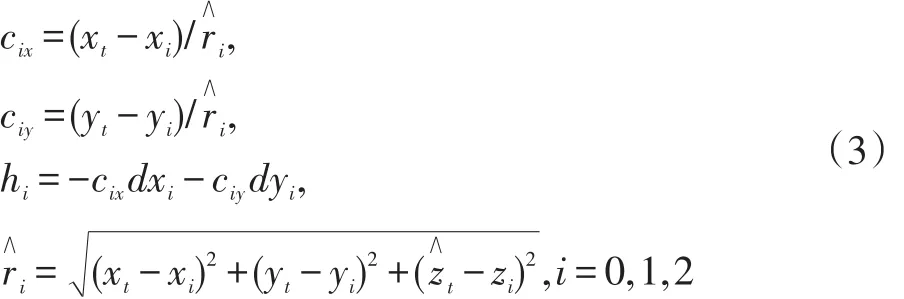
令：

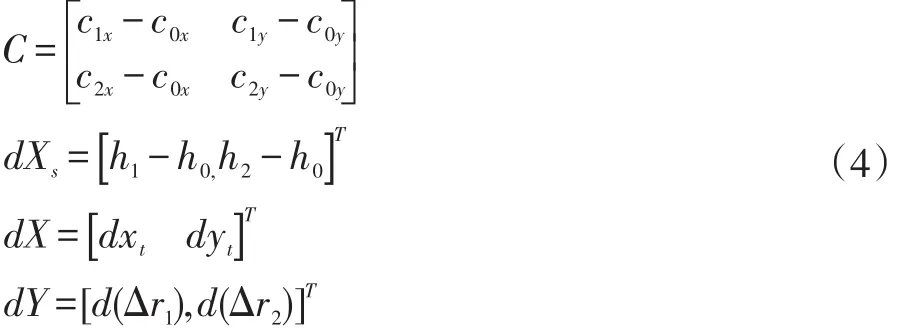
（2）式可写作：

用伪逆法求解得dX得：

令：

其中，dX表示辐射源的定位精度，dY表示距离差的测量误差。

设Δri经系统修正以后均值为0，dXs个元素互不相关，则定位误差的协方差为：

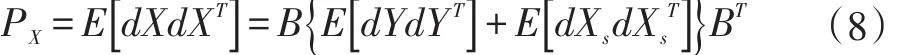
有：

设观测器载体的最大飞行速度为V，速度调整因子为ai,航向角为θi（i=0,1,2）,则 k 时刻的观测器坐标为：

其中P为优化后的参数集，Pc表示任意时刻的解空间的集合。

2 求解轨迹优化问题的粒子群算法

粒子群优化算法（PSO）由Eberhart博士和Kenne⁃dy于1995年提出，是一种群体智能算法，源于鸟类觅食的灵感，粒子群算法利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。它是群体智能算法中最简单的一种，具有精度高、收敛快等优点，这些优点非常适用于实时性强的问题。

对于三平台轨迹优化问题，将带求解的参数个数设为6，分别为这三个平台的航向角以子i当前飞行速度，pi是使得粒子i具有最好适应度的位置，pg为所有粒子中出现的最好的适应度对应的位置。在该问题中，适应度最好意味着当前位置下的GDOP值最小。第i个粒子在6维空间中的速度与位置的更新公式如下：

其中i∈(1,2,∙∙∙,n),d∈(1,2,∙∙∙,6)，w 为惯性权重，c1、c2位学习因子，pid为每个粒子到目前为止出现的最佳位置，pgd为所有粒子到目前为止所出现的最佳位置。

3 轨迹优化与目标估计

传统辐射源被动跟踪中，由于辐射源运动轨迹不定，而观测平台始终以固定的布站运动会导致测量误差逐渐积累，最终出现失跟的可能，为了减少滤波发散的影响，将轨迹优化加入到整个目标的被动跟踪过程中，使其成为一个闭环的过程，减少布站对精度的影响。

整个辐射源被动跟踪过程如下：

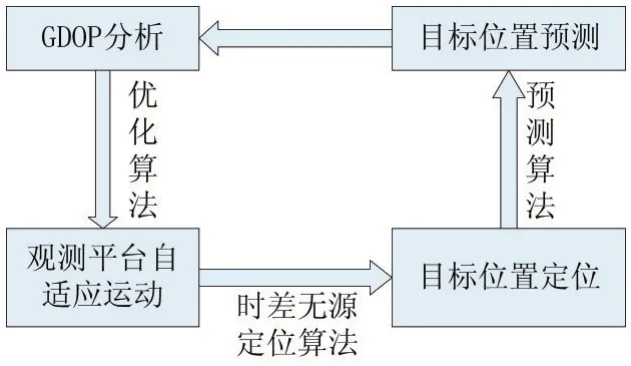
图1 辐射源被动跟踪过程

4 仿真实验与结果分析

4.1 仿真实验

在三平台二维空间中完成，测量时间间隔T=1s，到达时间测量精度设为20ns（对应的辐射源到副站与到主站之间的距离精度为6m，三个观测器以到三角形编队（基线夹角为 120°），三平台的初始位置为：（0,0,9），（13,7.5,9），（-13,7.5,9）（单位是 km）目标辐射源的初始位置为：（0,200,9.6）（km），考虑到信号可靠传输的影响，将主站与副站的距离限制在20公里内。同时，考虑到机载平台的机动性，将机载平台每时刻的转弯幅度定其上一状态的方向的±45°之间。对以下几种情况进行仿真（单位均为km/s）：

场景 1：辐射源速度为（0.2,-0.2）（km/s），观测器自适应运动。

场景2：辐射源在x方向速度为0.2km/s，在y方向初始速度为0.1km/s，加速度为0.001km/s2，即运动轨迹为抛物线形式，观测器自适应运动。

将以上两种情况与观测器按（0.2,-0.3）（km/s）的速度以固定轨迹运动做比较。

4.2 实验分析

图2中，左侧为用粒子群算法对观测器轨迹的实时优化图，蓝色线条为观测器轨迹，红色代表目标运动轨迹。可以看到，在基线长度未到达最大时，副观测器远离主观测器，使基线距离增大，该运动轨迹符合预期，当基线距离接近限定长度时，三观测器逐渐减小与目标之间的距离，最后当观测平台与目标处于精度较高的布站形式时，观测器将保持此状态，即尽可能使目标处于以副观测器连线为底边的等腰三角形的中垂线上。在图2的GDOP图中，蓝色曲线代表观测器轨迹实时优化后的GDOP图，黑色轨迹代表观测器按固定轨迹飞行时的GDOP图，经过轨迹优化后的目标跟踪精度明显高于按固定轨迹飞行时的跟踪精度。

图3中，左侧为用粒子群算法对观测器轨迹的实时优化图，蓝色线条为观测器轨迹，红色代表目标运动轨迹。可以看到，其观测器轨迹优化曲线与图2中大致相同，只是GDOP图略有差异，这是因为目标在y轴上做匀加速运动，而在某一时刻，目标的运动速度超过了观测器的最大速度，此时，观测器无法继续保持最优布站形式，所以GDOP图中的后半段的值有所上升，符合实际情况。

图2

图3

注：在观测器按固定轨迹飞行时，其在x轴上的速度与目标一致，而目标在y轴的初始速度比观测器低，其位置差会增加，所以在一段时间内对应的GDOP曲线呈上升趋势；当目标在y轴上的速度高于观测器速度时，其位置差会减小，GDOP呈下降趋势；当后期目标逐渐远离观测器时，GDOP值又会逐渐变大。

以上两种实验场景证明，用粒子群算法对观测平台进行实时轨迹优化是有效的，在观测器速度允许的情况下，可以对辐射源保持高精度的定位追踪，该方法相较于固定形式布站，有明显的优势。

5 结语

本文在时差无源定位体制下，对目标运动的情况，提出了一种基于粒子群算法的观测平台轨迹优化方法。将轨迹优化加入到目标被动跟踪的过程中，避免了滤波发散，满足了定位精度的要求。仿真结果证明，该方法作用下的定位跟踪精度明显高于观测器沿固定轨迹飞行时的跟踪精度。

参考文献：

[1]孙仲康，周一宇，何黎星.单多基地有源无源定位技术.北京：国防工业出版社，1996.5

[2]单月晖，孙仲康，皇甫堪.不断发展的无源定位技术.航天电子对抗2002（3）:36-42

[3]Martinescalona I,Barceloarroyo F.Impact of Geometry on the Accuracy of the Passive-TDOA Algorithm[J].2008:1-6.

[4]Musicki D,Kaune R,Koch W.Mobile Emitter Geolocation and Tracking Using TDOA and FDOA Measurements[J].IEEE Transactions on Signal Processing,2010,58（3）:1863-1874.

[5]王瀚.机载多平台时差无源定位系统若干关键技术研究[D].国防科学技术大学,2006.

[6]杨丽丽,孙晓闻.无人机载多站无源定位系统精度分析[J].中国电子科学研究院学报,2014,9（4）:348-352.

[7]潘烨炀,郭洁,张林颖,等.基于自适应遗传算法的优化布站方法研究[J].国外电子测量技术,2013,32（6）:62-64.

[8]B DSivazlian and R E Green.Effect of Instrument Siting and Coordinate Selection on GDOP in Target Tracking.AD/A-03183.