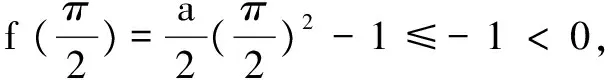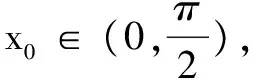利用导数化解数学中的问题
曾 美 陈国林
(1.赣州市蓉江新区潭东中学 341000;2.赣南师范大学科技学院 341000)
陈国林(1994.10-),男,安徽亳州人,本科,从事中学数学解题,中学数学教育研究.
一、证明超越不等式利用函数的单调性来破解
例1 利用函数的单调性证明: sinx 解析设f(x)=sinx-x,因为f′(x)=cosx-1,且cosx<1,x∈(0,π),所以f′(x)<0,f(x)在(0,π)上为减函数,故f(x) 评注此不等式是超越不等式,要想利用常规方法证明本题是难以进行的.若构造函数利用导数判断函数单调性,使用单调性予以证明则较为简单、快捷. 变式1 当x>0时,证明: 当x> 0时,f(x)>f(0)=0,即ln(1+x)>x- 例2 (2017年新课标全国Ⅰ卷理)已知函数f(x)=ae2x+(a-2)ex-x. (1)讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. 解析(1)由于f(x)=ae2x+(a-2)ex-x,故 f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1). ①当a≤0时,aex-1<0,2ex+1>0,从而f′(x)<0恒成立.f(x)在R上单调递减. ②当a>0时,令f′(x)=0,从而aex-1=0,得x=-lna. x(-∞,-lna)-lna(-lna,+∞)f′(x)-0+f(x)单调减极小值单调增 综上,当a≤0时,f(x)在R上单调递减; 当a>0时,f(x)在(-∞,-lna)上单调递减,在 (-lna,+∞)上单调递增. (2)由(1)知, 当a≤0时,f(x)在R上单调减,故f(x)在R上至多一个零点,不满足条件. 故当0 又f(x)在(-∞,-lna)上单调减,在(-lna,+∞)单调增,故f(x)在R上至多两个实根. 综上,0 注意到h(1)=0,所以g(t)在(0,1)上单调递增,在(1,+∞)上单调递减,即g(t)max=g(1)=1. (1)证明:当a≥1时,f(x)有唯一的零点; (2)若f(x)≥0,求实数a的取值范围. 解(1)略. ③当a≥1时,由(1)知,f(x)≥0. 综上,若f(x)≥0时,a的取值范围为[1,+∞). 评注二次求导的原因是导函数方程f′(x)=0无法用初等方程的求解方法求解,如果遇到的是超越方程,借用图解法大致判断解的位置,甚至通过观察获得特殊的解.在题目的设计当中一般二次求导后对于一阶导数是具有单调性的. 参考文献: [1]陈国林,寇桂晏.追踪导数高考涉及的证明问题[J].数理化解题研究,2016(12).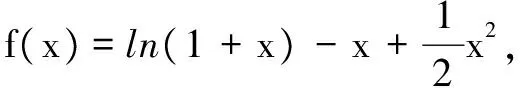
二、利用导数求解参数问题

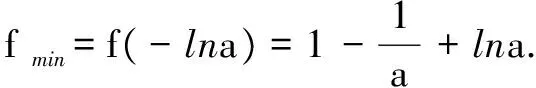

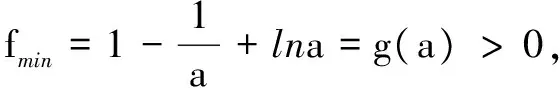
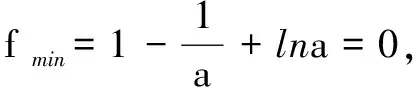






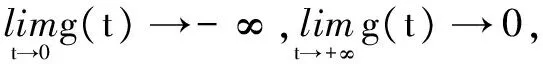


三、利用二次求导破解函数单调性